VC Is All You Need

//#define _ 0
//return ~~(0^_^0)~~
#include<vector>
#include<string>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cmath>
#include<map>

using namespace std;
#define ll long long 
void solve() {
	long long n, m;
	cin >> n >> m;
	if (n >= m + 2)cout << "No" << endl;
	else cout << "Yes" << endl;
}

signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int t;
	cin >> t;
	while (t--)solve();
}

Cut tree

Simulate according to the meaning of the question

//#define _ 0
//return ~~(0^_^0)~~
#include<vector>
#include<string>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cmath>
#include<map>

using namespace std;
#define ll long long
const int N = 1000010;
struct segment {
	int a[3];
}t[N<<2];
int n, cnt, x;
void build(int x, int l, int r) {
	if (l == r)return;
	if (r == l + 1) {
		build(t[x].a[0] = ++cnt, l, l);
		build(t[x].a[1] = ++cnt, r, r);
		return;
	}
	int len = (r - l) / 3 + 1;
	int a = l + len - 1, b = a + r >> 1;
	build(t[x].a[0] = ++cnt, l, a);
	build(t[x].a[1] = ++cnt, a + 1, b);
	build(t[x].a[2] = ++cnt, b + 1, r);
}
void solve() {
	cnt = 1;
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> x;
	build(1, 1, n);
	cout << cnt << endl;
}

signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int T;
	cin >> T;
	while (T--)solve();
}

Banzhuan

meaning of the title
The meaning of the title is to give an nnn cube. We need to put bricks in the cube so that its front view, left view and top view are an nn matrix, Moreover, when it is specified that the contribution of each brick is the position (xy2z), it should be noted that the calculated contribution of each brick is at the initial position, not at the stable position due to gravity
Problem solution
The most interesting point in the topic is that when calculating the contribution, we calculate the starting position of the sub, so we should put all the bricks at the top when calculating the maximum value
In this way, it is the highest contribution.
So the difficulty is how to calculate the minimum value. Because of the requirements specified in the title, the top view is also an nn square. In order to minimize, we should lay all the bottom layers
Then the cost of paving the first floor should be * * (1 + 2 + 3 +... + n)(12+22+32 +... + n2)1*
So how should we calculate those that are not the first layer?
First of all, the way we think of to make the front view and the left view both nn squares should be to spread a whole diagonal line. However, if it is a positive diagonal line, X and y are close. It can be known from junior high school knowledge that when x is close to y, the answer obtained must be greater than when the difference between X and Y is greater. For example, on row N and column n, the contribution of the positive diagonal line should be n3, The negative diagonal should be * * 1*n2 * *, so we can find that the sub diagonal is better than the main diagonal. Is there a better one? At this time, we can find that the point on all diagonals can also be replaced by the two on the edge

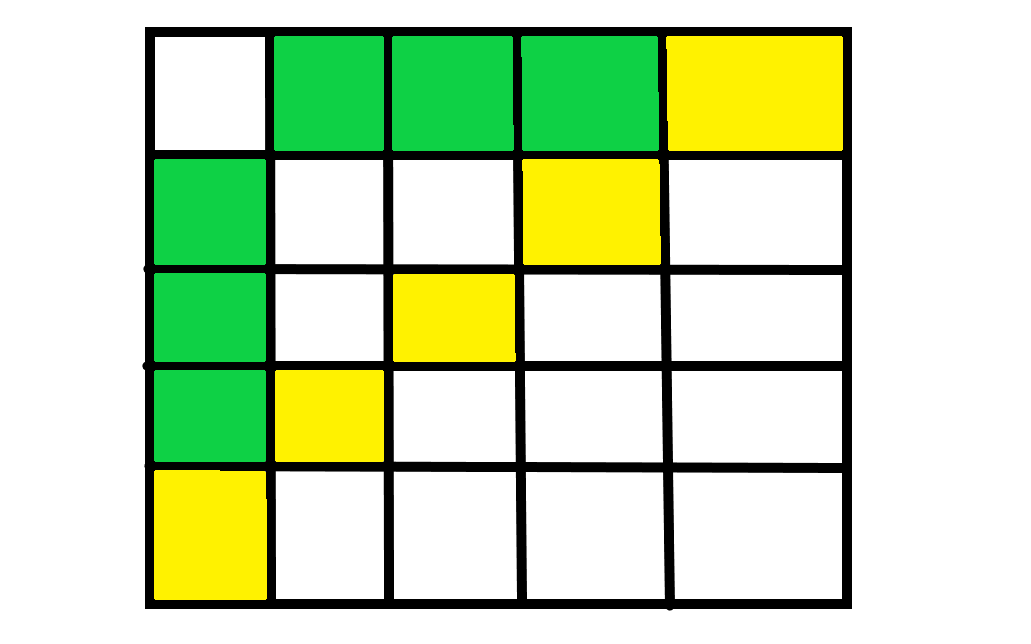
From the figure, we can find that all the Yellow parts can be replaced by the green parts. So how can we prove that this is the best
First of all, we don't have to consider the two parts on the edge. Second, for the rest, it should be
(2(n-1)2)+...+(22(n-1));
And the green part should be
22+32+...(n-1)2+2+3+...(n-1)
The subtraction should be
(n-1)2+2(n-2)2+...+(n-2)22-(n-1)-(n-2)-...-2
When n > 2, it is greater than zero
Therefore, the green color filling method should be the best

//#define _ 0
//return ~~(0^_^0)~~
#include<vector>
#include<string>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cmath>
#include<map>
using namespace std;
#define int long long
const int mod = 1e9 + 7;
int qmi(int a, int b) {
        int res = 1;
        while (b) {
            if (b & 1)res = (res * a) % mod;
            b >>= 1;
            a = (a * a) % mod;
        }
        return res;
    }
void solve() {
        int n; cin >> n;
        n = n % mod;
        int n1 = (n * (n + 1) % mod * ((2 * n % mod + 1) % mod)) % mod * qmi(6, mod - 2) % mod;
        int n2 = n * (n + 1) % mod * qmi(2, mod - 2) % mod;
        int n3 = n * n % mod;
        int ma = n1 * n2 % mod * n3 % mod;
        int n4 = (n - 1 + mod) % mod * (2 + n) % mod * qmi(2, mod - 2) % mod;
        int n5 = (n * (n + 1) % mod * ((2 * n % mod + 1) % mod) % mod * qmi(6, mod - 2) % mod - 1 + mod) % mod;
        int n6 = (n - 1 + mod) % mod * (2 + n) % mod * qmi(2, mod - 2) % mod;
        int n7 = n1 * n2 % mod;
        int mi = n7 + (n4 + n5) % mod * n6 % mod;
        cout << mi % mod << endl << ma % mod << endl;
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int T;
	cin >> T;
	while (T--)solve();
}