When it comes to hash, I believe many students are familiar with it. Hash (hash, hash) function maps data of any length to a field of finite length. It is widely used in algorithm competitions.
How does the hash function map arbitrary length data to finite length fields? We usually take the modulus of a number, but it should be noted that, for example, we use X to take the modulus of N. when x is a positive number, it is OK to take the modulus directly, but when x is a negative number, the value after taking the modulus directly is negative. We should add n to the modulus and then take the modulus of N. of course, sometimes there are conflicts. There are generally two methods to deal with conflicts: one is the zipper method, and the other is the open addressing method, I will analyze these two implementations in detail below
Let's first look at the pull-down chain method:
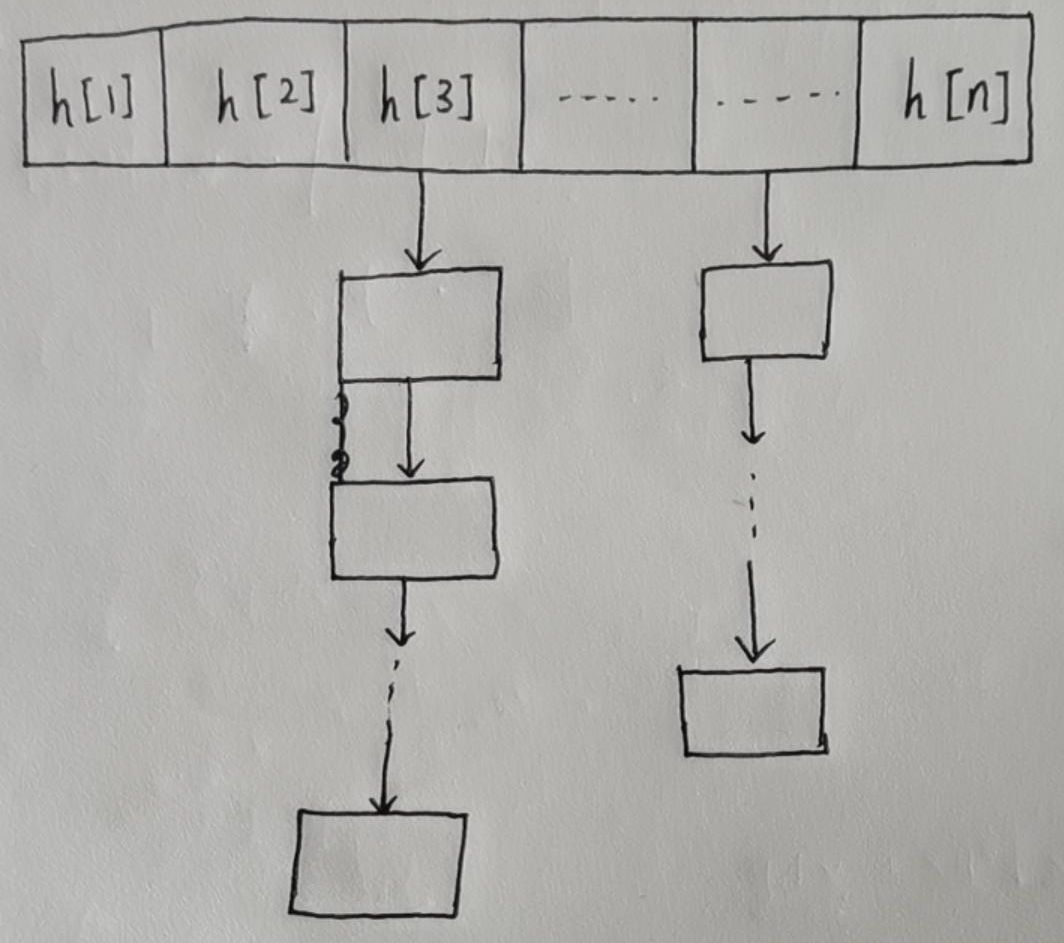
It looks like this. If m and n become k after hash transformation, they will become part of the chain under h[k]. h[k] stores the position of the head node of each linked list. The specific implementation is to simulate the linked list with an array.
When you need to add an element, you only need to add the element after hash transformation to the array. If you need to find an element, you need to find it in the chain under the mapping value of the corresponding hash function.
Let's introduce the open addressing method to construct the hash table. The hash function is basically similar, but the way to find and add elements changes greatly. It doesn't need to add a chain under each h array. It just needs to find the empty bits, and then find them one by one according to the rules. If x is in the hash table, the find function returns the array subscript that stores X,
If x is not in the hash table, it returns the location where x should be stored (that is, the first empty bit found according to the search rules)
An example and two implementation methods are given below:
Maintain a collection and support the following operations:
- I x, insert a number {X;
- Q x, query whether the number x has appeared in the set;
Now you need to perform N} operations and output the corresponding results for each query operation.
Input format
The first line contains the integer N, which represents the number of operations.
Next, there are N lines, and each line contains an operation instruction. The operation instruction is one of ^ I x, Q x ^.
Output format
For each query instruction Q x, a query result is output. If Q x , has appeared in the set, then , Yes is output, otherwise , No is output.
One line for each result.
Data range
1≤N≤10^5
−10^9≤x≤10^9
Input example:
5 I 1 I 2 I 3 Q 2 Q 5
Output example:
Yes No
Zipper simulation hash table
#include<iostream>
#include<cstring>
using namespace std;
const int N=100003;
int h[N],ne[N],e[N],idx;
void insert(int x)
{
//h[k] stores the subscript of the first element in the linked list generated by the node K
int k=(x%N+N)%N;
e[idx]=x;
ne[idx]=h[k];
h[k]=idx++;
}
bool query(int x)
{
int k=(x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i])
if(e[i]==x)
return true;
return false;
}
int main()
{
int n;
cin>>n;
string c;
int d;
memset(h,-1,sizeof(h));
for(int i=1;i<=n;i++)
{
cin>>c>>d;
if(c=="I") insert(d);
else
{
if(query(d)) printf("Yes\n");
else printf("No\n");
}
}
return 0;
}
//Open addressing analog hash table
#include<iostream>
#include<cstring>
using namespace std;
const int N=200003,null=0x3f3f3f3f;
int h[N];
//Note: if x exists, the index of the array where x is located will be returned; if it does not exist, the position where x should be inserted will be returned
int find(int x)
{
int t=(x%N+N)%N;
while(h[t]!=null&&h[t]!=x)
{
t++;
if(t==N) t=0;
}
return t;
}
int main()
{
int n;
cin>>n;
string c;
int d;
memset(h,0x3f,sizeof(h));
for(int i=1;i<=n;i++)
{
cin>>c>>d;
int k=find(d);
if(c=="I") h[k]=d;
else
{
if(h[k]==d) printf("Yes\n");
else printf("No\n");
}
}
return 0;
}Here is another hash method different from the above two methods:
String hash:
First give an example, which is explained in detail in the code:
Given a string with a length of , n , and , m , queries, each query contains four integers , l1,r1,l2,r2. Please judge whether the string substrings contained in [l1,r1][l1,r1] and [l2,r2][l2,r2] are exactly the same.
The string contains only upper and lower case English letters and numbers.
Input format
The first line contains integers , n , and , m, representing the length of the string and the number of queries.
The second line contains a string with a length of {n}, which contains only uppercase and lowercase English letters and numbers.
The next ^ m ^ line contains four integers ^ L1 and R1, representing the two intervals involved in a query.
Note that the position of the string is numbered starting from {11}.
Output format
One result is output for each query. If the two string substrings are exactly the same, output "Yes", otherwise output "No".
One line for each result.
Data range
1≤n,m≤10^5
Input example:
8 3 aabbaabb 1 3 5 7 1 3 6 8 1 2 1 2
Output example:
Yes No Yes
#include<iostream>
#include<cstring>
using namespace std;
typedef unsigned long long ULL;
const int N=100010,P=131;
//p usually select 131 or 13331; mod2^64 is usually selected, and exploding in the ULL will not affect the result
int n,m;
char s[N];
ULL h[N],p[N];//h[i] stores the hash value of the first I characters, and p[i] stores the i-th power of p
ULL fun(int l,int r)
{
return h[r]-h[l-1]*p[r-l+1];
}
int main()
{
cin>>n>>m>>s+1;
p[0]=1;
for(int i=1;i<=n;i++)
{
p[i]=P*p[i-1];
h[i]=h[i-1]*P+s[i];
}
int l1,r1,l2,r2;
while(m--)
{
cin>>l1>>r1>>l2>>r2;
if(fun(l1,r1)==fun(l2,r2)) printf("Yes\n");
else printf("No\n");
}
return 0;
}Now I will analyze the train of thought and difficult points of this problem:
We convert each character into a number in p-ary, and then take the remainder of 2 ^ 64;
Note: p often takes 131 or 13331. Taking these two prime numbers can reduce the probability of conflict. After doing enough preparatory work, we will test our character at this time. It is no problem for most questions to use these two numbers. Another thing to note is that 2 ^ 64 is exactly the range of unsigned long long, so we can define the data type as unsigned long long, In this way, even if they explode during the operation, they will not affect the result.
When we process the hash value from l to r, we use the form of prefix and. The left side of the string is high and the right side is low
The hash function is analyzed below:
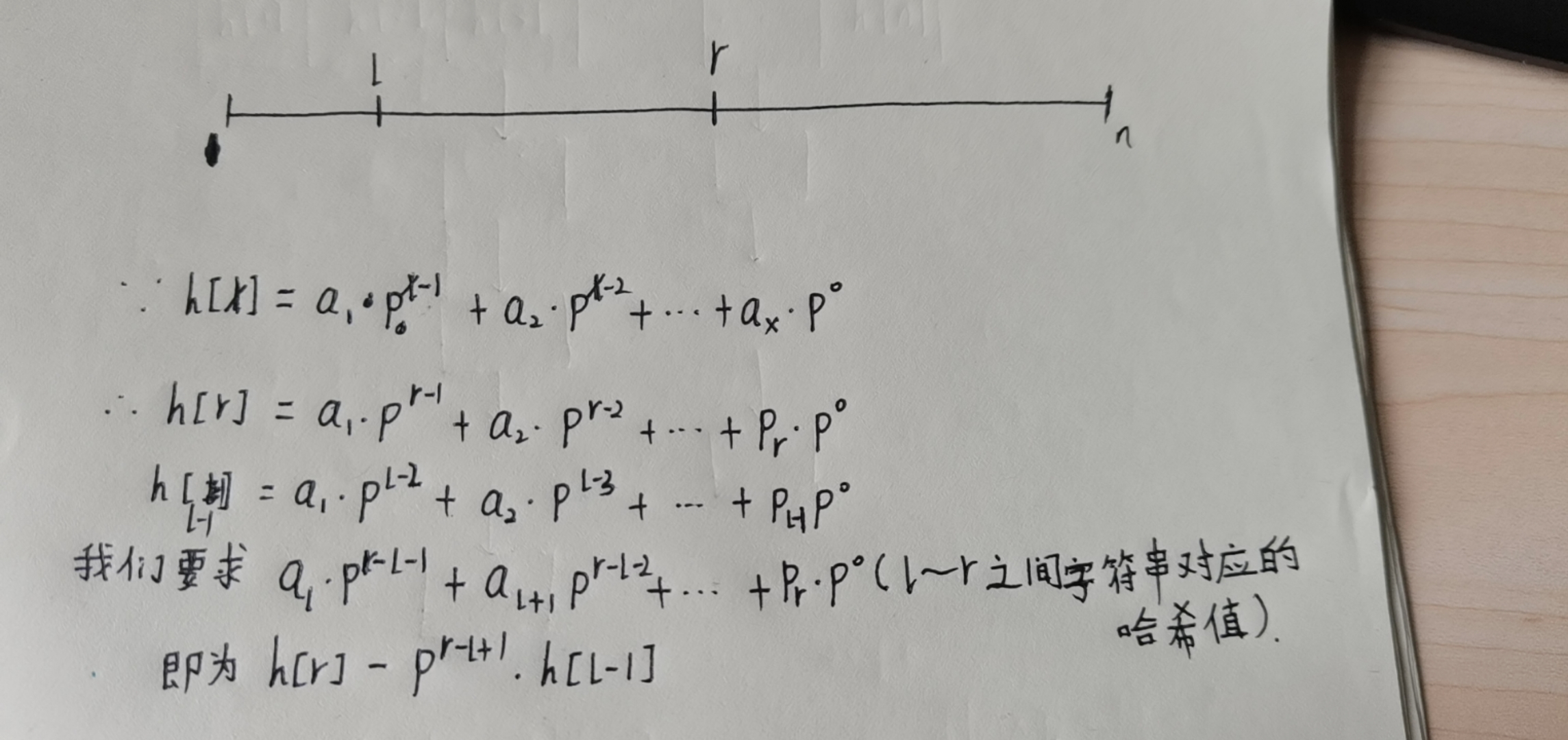
The above is my understanding of hash. I hope you can like it!