1, Underlying data structure of hash table
- jdk1. After 8, the underlying data structure of the hash table is array + linked list + red black tree.
- The reason why linked lists are introduced is to solve hash conflicts.
- The reason why red black tree is introduced is to increase the efficiency of search.
- If there is no hash conflict, the lookup time complexity of the hash table should be O(1). If there is a hash conflict, the lookup time complexity should be O(n). Once the red black tree is introduced, the lookup time complexity will become O(logn).
- Two problems arise:
- Why not use the red black tree directly, but only when the depth of the linked list is greater than or equal to 8 and the array capacity is greater than or equal to 64.
- Why use red black tree instead of binary sort tree and AVL tree (balanced binary lookup tree).
- First, why not use the red black tree directly
- The reason is very simple, because if the red black tree is used directly, the red black tree has a self balancing operation (left rotation, right rotation, color change), which is a waste of CPU resources. And according to the source code of the hash table, the probability that the node depth of the linked list can reach 8 is very small. Therefore, only in the case of large amount of data can red black trees be used.
- Second question, why use red black tree instead of binary sort tree and AVL tree:
- First, let's talk about the definitions of these three kinds of trees:
- Binary sort tree (as shown below):
- Binary sort tree (also known as binary lookup tree):
1) If the left subtree is not empty, the values of all nodes on the left subtree are less than those of the root node.
2) If the right subtree is not empty, the values of all nodes on the right subtree are greater than those of the root node.
3) The left and right subtrees are also binary sort trees.
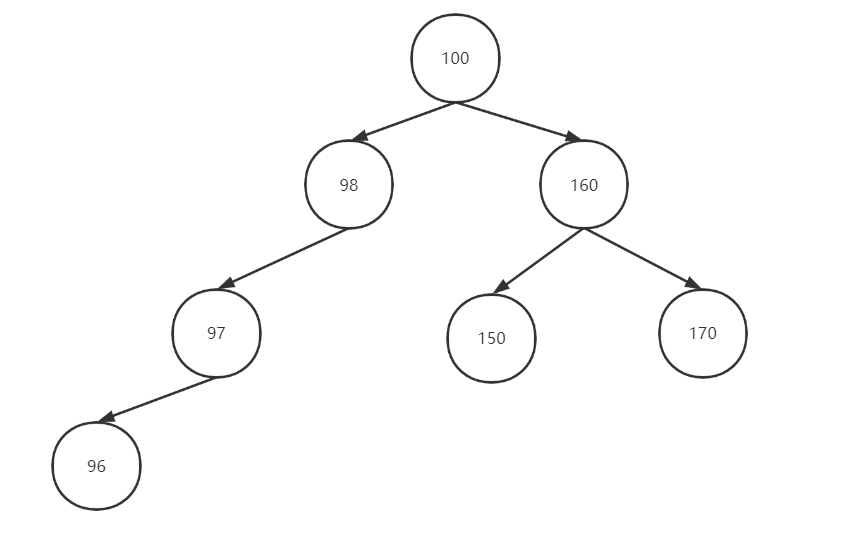
- Such a tree is also a binary sort tree. Obviously, its left sub tree has degenerated into a linked list. Isn't it cool. So you can't use binary sort trees.
- Red black tree and AVL tree (balanced binary lookup tree):
- AVL tree (balanced binary lookup tree)
- AVL tree actually adds self balancing operation on the basis of binary search tree.
- Generally, the balance factor difference is used to judge whether it is balanced or not, and the balance is realized by rotation.
- It is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, and both the left and right subtrees are a balanced binary tree (as shown in the figure below).
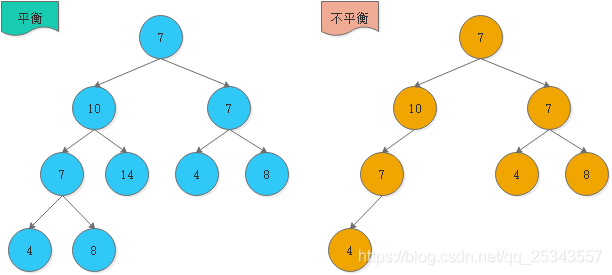
- As shown in the figure above, the binary sort tree on the right is degraded into a linked list, while the AVL tree on the left solves this defect.
- Red black tree:
- In fact, red black tree is also a balanced binary tree, but it is not as balanced as AVL tree. It uses color to identify whether balance operation is required. Moreover, red black tree has no specific requirements for the height difference between left and right subtrees, so it can be said that it is a weakly balanced binary tree
- Therefore, compared with the strict AVL tree, it has less rotation times, so when there are many search, insert and delete operations, we use red black tree.
- Finally, the definition of red black tree is attached:
- Each node is either red or black
- The root node is black
- Each leaf node is black
- If a node is red, its two sons are black
- There can be two connected black nodes, but not two connected red nodes
- For each node, all paths from the node to its descendants contain the same number of black nodes
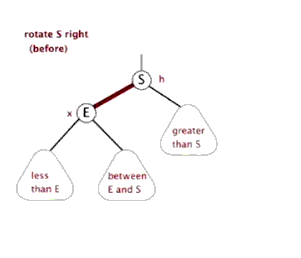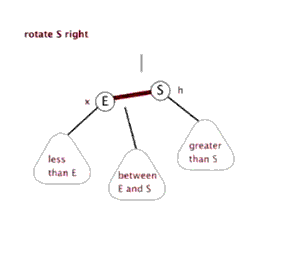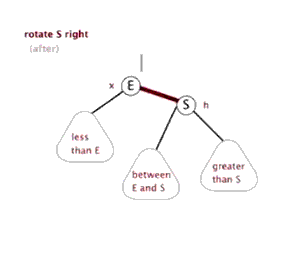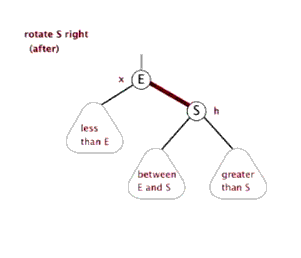
- Self balancing operation: discoloration, left rotation, right rotation
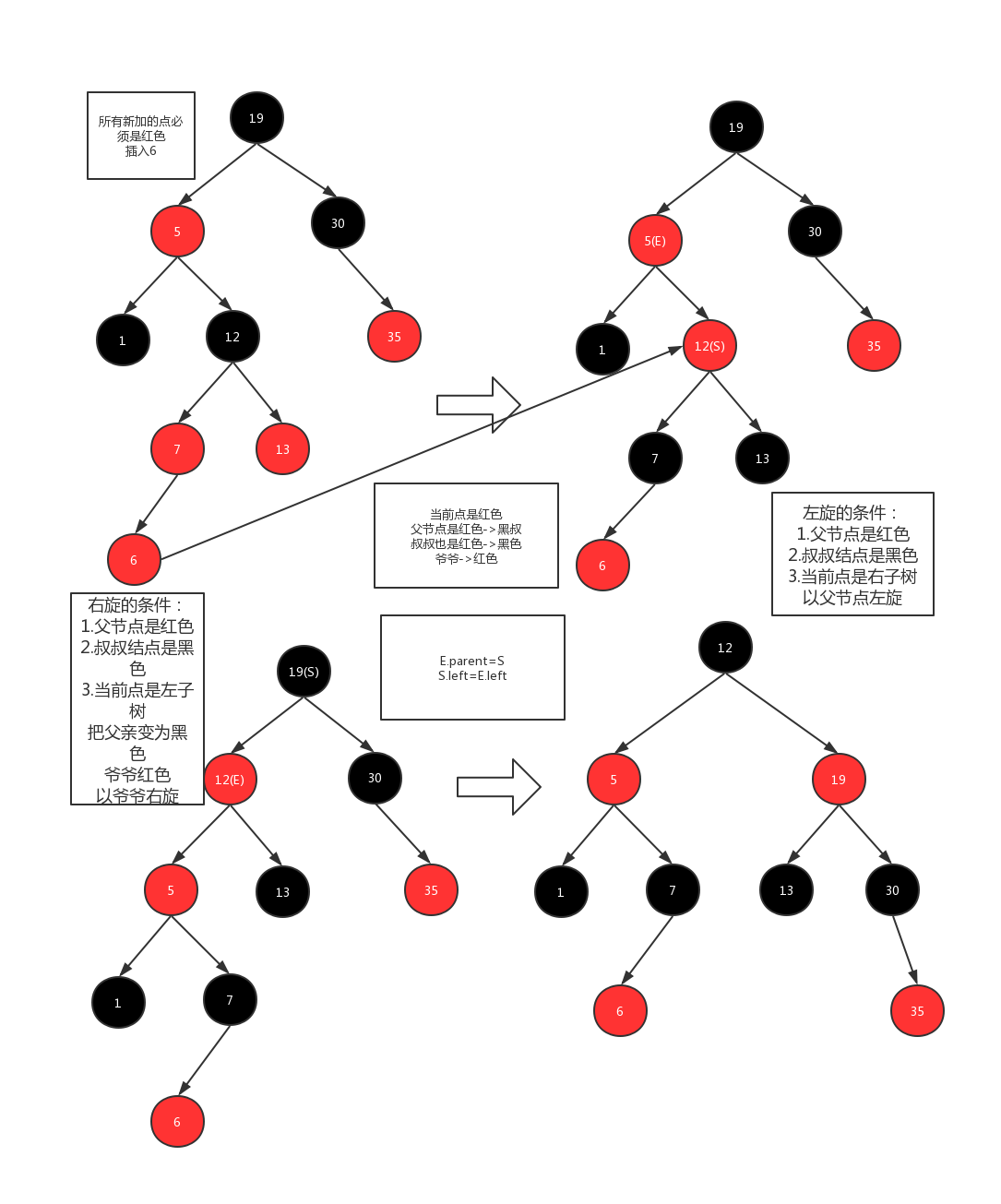
- Sinistral
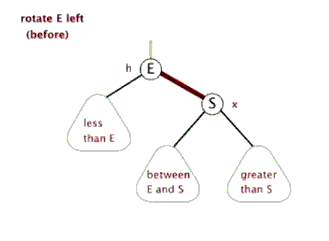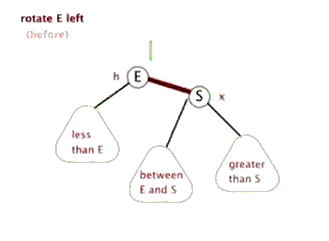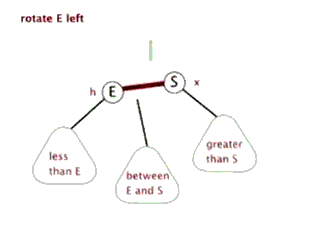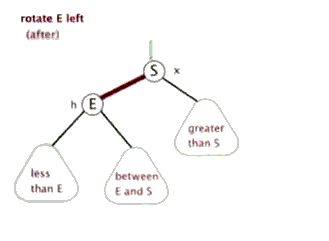
- Dextral
2, put method of hash table
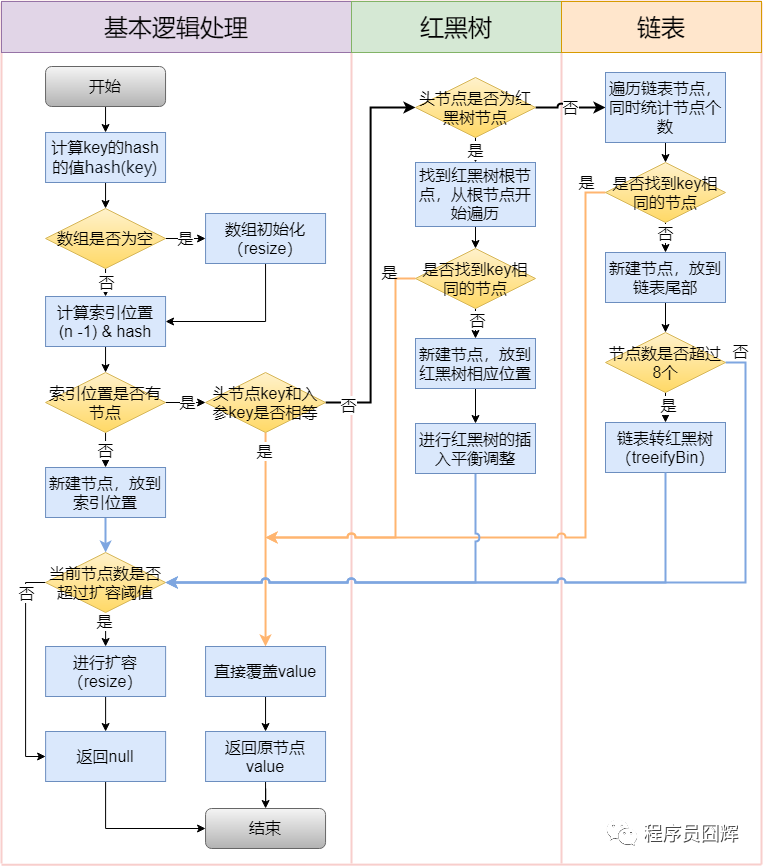
- Here we need to declare that the hash table is initialized during the put() method.
- There are three situations: normal insertion, insertion of the first element, and capacity expansion after insertion
- Judge whether there is a duplicate value. If there is a duplicate value, replace it and return the previous value
public V put(K key, V value) {
//The putVal () method will be called here
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//If not initialized, expand the capacity
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
//Determine whether the current index is null
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
//Judge whether the first node is repeated
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
//Replace if duplicate
e = p;
else if (p instanceof TreeNode)
//Judge whether it is a red black tree. If so, replace it according to the method of red black tree
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
//Traversal linked list
for (int binCount = 0; ; ++binCount) {
//The last one is a null value, which is inserted at the end
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
//If there are duplicate values in the linked list, it will end
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
//If e is not empty, it indicates that there is a duplicate value. Replace it and return the old value
//You can try the following code
//HashMap<String,String> map = new HashMap();
//map.put("aaa", "Beijing");
//map.put("aaa", "Shanghai");
//map.put("aaa", "Hegang");
//System.out.println(map.put("aaa", "Shuangyashan");
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
//There are no duplicate values
++modCount;
//If the number is larger than the array length * 0.75, expand the capacity
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
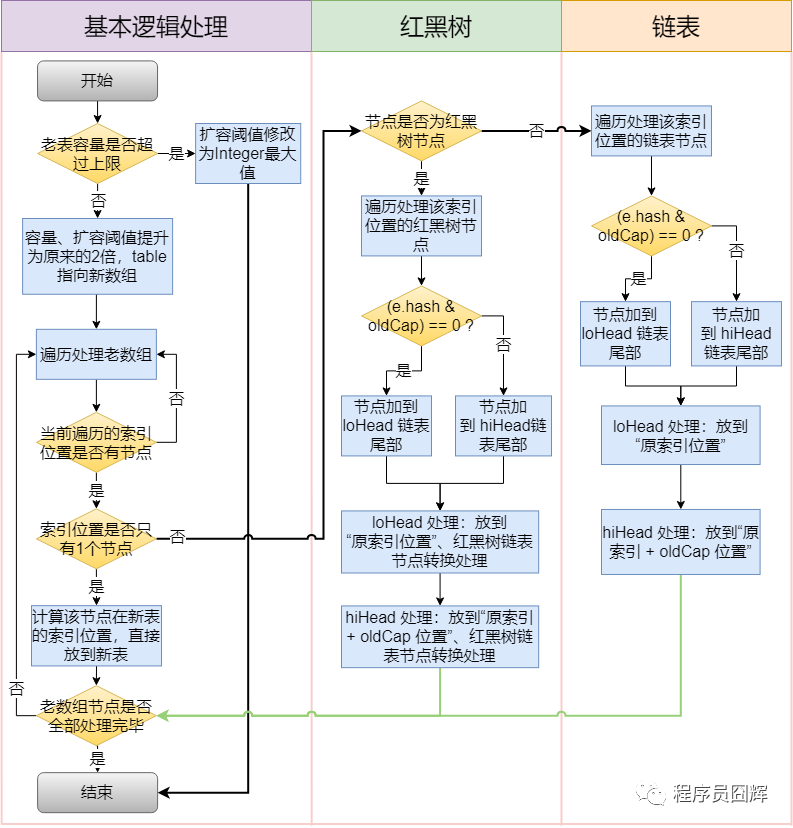
3, Capacity expansion of hash table (resize())
final Node<K,V>[] resize() {
//First, let's see if the underlying array is null
Node<K,V>[] oldTab = table;
//If it is null, set the size of the original array to 0
int oldCap = (oldTab == null) ? 0 : oldTab.length;
//Threshold of old array
int oldThr = threshold;
//Length and threshold of the new array
int newCap, newThr = 0;
if (oldCap > 0) {
//The current capacity has exceeded the maximum value and cannot be expanded
if (oldCap >= MAXIMUM_CAPACITY) {
//Update the threshold and return
threshold = Integer.MAX_VALUE;
return oldTab;
}
//If the maximum value is not exceeded after the expansion of the array, the threshold is also * 2
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else {// zero initial threshold signifies using defaults
//This is when it has not been initialized, that is, when it is put ting the first element
//The length of the new array is the default
newCap = DEFAULT_INITIAL_CAPACITY;
//Threshold for new array
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
//Here is to judge whether the new threshold has been calculated. If
//Else if (oldthr > 0) placed in threshold
//This code needs to be calculated
newCap = oldThr;
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
//Here is the index operation of updating elements after capacity expansion.
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
//Here we need to see if it is a tree node
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
- Is HashMap capacity expansion time limit inserted or expanded first?
- Expand the capacity first.
4, How to make hash table thread safe
- Add the synchronized keyword to all the methods. (Hashtable)
- Collections. Package Hashmap with synchronized map.
eg: use map = collections synchronizedMap(new HashMap()); - Using ConcurrentHashMap, the source code analysis will be written later






