HashMap first appeared in JDK 1.2, and the underlying implementation is based on hash algorithm. HashMap allows null keys and null values. When calculating the hash value of HA key, the hash value of null key is 0. HashMap does not guarantee the order of key value pairs, which means that the order of key value pairs may change after some operations. In addition, it should be noted that HashMap is a non thread safe class, which may have problems in a multithreaded environment.

HashMap underlying data structure

In the early JDK version, HashMap is composed of array + linked list. Array is the main body of HashMap, and linked list mainly exists to solve hash conflicts. When storing elements in HashMap, objects with the same hash value will form a linked list and put them in the corresponding array elements. However, the time complexity of linked list query elements is O(n), so the more linked list elements, the lower the query efficiency.

Based on the above background, in JDK8, HashMap introduces the third data structure - red black tree. Red black tree is a binary tree close to balance, and its query time complexity is O(logn), which is higher than the query efficiency of linked list. Why not directly use red black tree instead of linked list? This is because the cost of maintaining the red black tree itself is also relatively high. Each element inserted may break the balance of the red black tree, which requires the red black tree to maintain its own balance through left-hand, right-hand and color change operations when inserting data. Therefore, in HashMap, the conversion of linked list to red black tree needs to meet certain conditions.

1. Source code definition and structure diagram of array, linked list and red black tree in HashMap
The following source code definition is based on the JDK8 version. First, let's use the structure diagram to understand the data structure definition of HashMap.

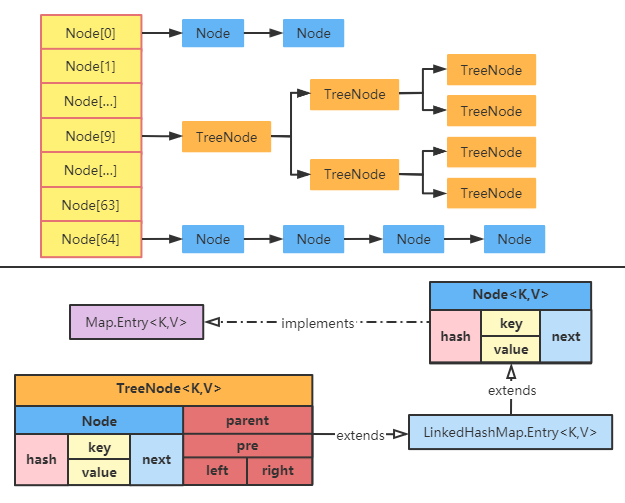
From the diagram, we can see that HashMap is composed of array, linked list and red black tree. JDK8 adopts the data structure of red black tree to optimize, making the access speed of HashMap faster.

• Array definition:

  // array
  transient Node<K,V>[] table;
  

• Single linked list node definition:

  static class Node<K,V> implements Map.Entry<K,V> {
      final int hash; // The value obtained by hashing the hashCode value of the key is stored in the Node to avoid repeated calculation
      final K key;
      V value;
      Node<K,V> next; // Store the reference to the next Node, single linked list structure
      Node(int hash, K key, V value, Node<K,V> next) {
          this.hash = hash;
          this.key = key;
          this.value = value;
          this.next = next;
      }
  	public final K getKey()        { return key; }
      public final V getValue()      { return value; }
      public final String toString() { return key + "=" + value; }
      public final int hashCode() {
          return Objects.hashCode(key) ^ Objects.hashCode(value);
      }
      public final V setValue(V newValue) {
          V oldValue = value;
          value = newValue;
          return oldValue;
      }
      public final boolean equals(Object o) {
          if (o == this) return true;
          if (o instanceof Map.Entry) {
              Map.Entry<?,?> e = (Map.Entry<?,?>)o;
              if (Objects.equals(key, e.getKey()) &&
                  Objects.equals(value, e.getValue()))
                  return true;
          }
          return false;
      }
  }
  

• Red black tree node definition:
  Treenode < K, V > inherits from LinkedHashMap Entry < K, V >, and LinkedHashMap Entry < K, V > is HashMap again Subclass of node < K, V >

  static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
  	TreeNode<K,V> parent;
  	TreeNode<K,V> left;
  	TreeNode<K,V> right;
  	TreeNode<K,V> prev;
  	boolean red;
  	TreeNode(int hash, K key, V val, Node<K,V> next) {
  	    super(hash, key, val, next);
  	}
  	// ... omit other function methods
  }
  

2. Use of linked list and red black tree in HashMap

After understanding the definition of data structure, let's take a look at how to use linked list and red black tree in HashMap?

• Use linked list to deal with hash conflict: objects with the same hash value will have the same index position calculated by addressing algorithm. Therefore, if you want to insert multiple objects at the same element position, you need to use linked list structure

• Linked list tree: when the number of linked list nodes is greater than or equal to 8 (tree_threshold), the linked list tree function final void treeifybin (node < K, V > [] tab, int hash) will be triggered. However, in this function, it will judge whether the array length is less than 64 (min_tree_capability). If it is less than 64, only array expansion will be performed, In other words, the linked list tree operation will be performed only when the array capacity is greater than or equal to 64. Based on this mechanism, the performance consumption caused by linked list tree in the case of relatively small amount of data in HashMap is avoided. In other words, when the capacity of HashMap is small, it will temporarily maintain more elements in the linked list through the capacity expansion mechanism

• Red black tree to linked list: when the number of red black tree node elements is less than or equal to 6 (UNTREEIFY_THRESHOLD), the red black tree will be converted to linked list

  Next, through the source code and comments of the putVal method of HashMap, we focus on understanding the above-mentioned use of linked list to deal with hash conflict, linked list tree, and red black tree to linked list.

  final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
  	Node<K,V>[] tab; Node<K,V> p; int n, i;
  	if ((tab = table) == null || (n = tab.length) == 0)
  		n = (tab = resize()).length; // If there are no elements in the array table or the length is 0, call the capacity expansion function to initialize the array, assign the array to tab, and then assign the array length to n
  	if ((p = tab[i = (n - 1) & hash]) == null) // (n - 1) & hash is the hash addressing algorithm, which assigns the addressed element to p
  		tab[i] = newNode(hash, key, value, null); // If the current index position (i) of the array is null, the key value is directly inserted into that position
  	else { // The current index position of the array is not null
  		Node<K,V> e; K k; // Redefine a Node and a K
  		if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
  			e = p; // If the corresponding data already exists (the hash is equal and the key value is equal), assign the Node of the position to e
  		else if (p instanceof TreeNode) // Judge whether the type of Node in the current location is TreeNode
  			e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); // Insert an element into the red black tree
  		else {
  			// Let's start traversing the linked list of the current position in the array
  			for (int binCount = 0; ; ++binCount) { // Unconditional loop. binCount is used to record the number of nodes in the linked list (it starts from 0 and can also be regarded as the index number)
  				if ((e = p.next) == null) { // When node When next is null, it indicates that the end node of the linked list is found
  					p.next = newNode(hash, key, value, null); // Insert the key value directly into the tail of the linked list
  					if (binCount >= TREEIFY_THRESHOLD - 1) // After completing the insertion action, judge whether the index number of the linked list is greater than or equal to (8-1), that is, whether the node tree of the linked list is greater than or equal to 8
  						treeifyBin(tab, hash); // true to perform the linked list tree operation.
  						// Note that the treeifyBin function will judge whether the array length is less than 64. If it is less than 64, only the array expansion operation will be carried out, that is, the linked list tree operation will be carried out only when the array capacity is greater than or equal to 64
  					break;
  				}
  				if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
  					break; // If the corresponding data already exists (the hash is equal and the key value is equal), jump out directly. Note: the Node of this position has been assigned to e
  				p = e; // If the above conditions are not met, e is assigned to p to find subsequent nodes
  			}
  		}
  		// If e is not empty, a Node to store key value is found. When the key is the same, the value value is overwritten
  		if (e != null) {
  			V oldValue = e.value;
  			if (!onlyIfAbsent || oldValue == null)
  				e.value = value;
  			afterNodeAccess(e);
  			return oldValue;
  		}
  	}
  	++modCount;
  	if (++size > threshold)
  		resize(); // When the size of the HashMap is greater than the critical value, you need to adjust the capacity of the array. Note: during data expansion, if it is found that the number of red black tree node elements is less than or equal to 6, the red black tree will be converted into a linked list
  	afterNodeInsertion(evict);
  	return null;
  }
  

3. Practical verification
Through the above source code analysis, do you have a clear understanding of the underlying data structure of HashMap? Let's strike while the iron is hot and further observe the changes of the internal data structure of HashMap through a piece of test code.

@Test
public void hashMap() {
    Map<String, String> map = new HashMap<>(32); // The initialization capacity is 64. Interested friends can try 16 and 32
    List<String> list = Arrays.asList("A646", "9C9B", "FAF4", "674C", "5DCD", "C504", "555F", "F164"); // The array index position is 9
    for (String key : list) { map.put(key, key); }
    map.put("440A", "440A"); // When adding this element to HashMap, the linked list tree operation, treeifyBin(tab, hash), will be triggered;
    map.put("531D", "531D"); // The index position of the key is also 9. At this time, the put data will be maintained in the red black tree, e = ((treenode < K, V >) P) putTreeVal(this, tab, hash, key, value);
    // map.put("FDF1", "FDF1"); //  When the initialization capacity is 16, observe the difference between inserting and not inserting the element
    // Remove the four elements, and there are six nodes in the tree
    map.remove("A646"); map.remove("9C9B"); map.remove("FAF4"); map.remove("674C");

    // Continue to add more elements to force the HashMap to expand. Note that the index position of these elements added later is not 9
    List<String> list2 = Arrays.asList(
            "A", "B", "C", "D", "E", "F", "G", "H", "J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X",
            "Y", "Z", "AA",  "AB", "AC", "AD", "AE", "AF", "AG", "AH", "AI", "AJ", "AK", "AL", "AM", "AN", "AO", "AP", "AQ");
    for (String key : list2) { map.put(key, key); }
    map.put("AR", "AR"); // Adding more elements will trigger HashMap capacity expansion. During capacity expansion, it is found that the tree node length at the position of array index 9 is equal to 6, so the red black tree will be degraded into a linked list
    System.out.println(map);
}

You can observe the changes of data step by step through DeBug in the editor.

Implementation principle of HashMap perturbation function

The hashCode value of the object is of type int, so theoretically, we can directly use the hashCode value as the array subscript without collision. However, the value range of this hashCode is [- 2147483648, 2147483647], with a length of nearly 4 billion. No one can initialize the array so large, and there is no room for memory.

Since the hashCode value of the string cannot be directly used as a subscript, can we modulo the hashCode value and the data length to obtain a subscript value? Theoretically, it is feasible, but this will lead to the problem of insufficient hash of element position and serious element collision.

Therefore, the hashCode value is not directly used in the HashMap source code, but a disturbance calculation is performed on the hashCode value. In this way, when the array length is relatively small, it can also ensure that the high and low hashCode values participate in the hash calculation, increasing the randomness.

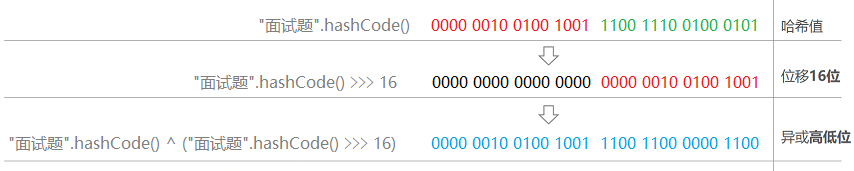
In JDK 8, the perturbation function is implemented through the high 16 bits of the hashCode() of the key and the low 16 bits of the exclusive or: (H = k.hashCode()) ^ (H > > > 16). The purpose of using perturbation function is to increase randomness, make data elements more balanced hash and reduce collision. The source code is as follows:

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); // Shift the hashCode value to the right by 16 bits, and then perform XOR operation with the original hashCode value
}

The following figure takes the string "interview question" as an example to show the process of perturbation operation of a string.

How to determine the capacity of the array table in the HashMap?

The default initial capacity of table in HashMap is 16 (static final int default_initial_capacity = 1 < < 4;), However, when initializing HashMap, it is recommended to specify the initial value size. The maximum limit is 1 < < 30 (static final int maximum_capability = 1 < < 30).

1. Specify initialization capacity

When we create new HashMap and specify initialCapacity, JDK will help us calculate the first power greater than initialCapacity. The source code is the deduction process as follows:

/**
 * Take the first power greater than 2 of cap, such as 6 - > 8; 10 -> 16;  17 -> 32
 * @param cap
 * @return
 */
static final int tableSizeFor(int cap) {
    // First, the purpose of minus one operation is to reduce the input parameter to a power number less than 2 (e.g. 8, 16, 32, etc.)
    // For example, if we pass in 10, the corresponding binary is 00000000 00000000 00000000 00001010
    int n = cap - 1;
    // After reduction
    // 00000000 00000000 00000000 00001001  -> 9

    n |= n >>> 1;
    // Shift right 1 bit
    // 00000000 00000000 00000000 00000100
    // After that, it will "or" with itself, that is, the above two binary phases "or"‘ Or operation: as long as one of the two values participating in the operation is 1, its value is 1
    // 00000000 00000000 00000000 00001101
    n |= n >>> 2;
    // Shift 2 bits to the right again
    // 00000000 00000000 00000000 00000011
    // The above two binary phases are 'or' again
    // 00000000 00000000 00000000 00001111 / / set all the low bits to 1, and we can see the effect we want
    n |= n >>> 4;
    // Shift 4 bits to the right again
    // 00000000 00000000 00000000 00000000
    // The above two binary phases are 'or' again
    // 00000000 00000000 00000000 00001111
    n |= n >>> 8;
    // The operation is the same as above
    n |= n >>> 16;
    // The operation is the same as above

    int result = (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    // After that, the + 1 operation is performed on the calculated number
    // 00000000 00000000 00010000 / / + 1 becomes a power number
    return result;
}

So why should the array length be guaranteed to the power of 2?

• Only when the array length is to the power of 2, H & (length-1) is equivalent to h% length, and the efficiency of bit operation is much higher than that of hash modular operation;
• If the length is not the power of 2, for example, if the length is 15, then the length - 1 is 14 and the corresponding binary is 1110. When the binary with h is' and ', the last bit is 0, and 00010011010110011111101 can never store elements. The space cost is quite large. What's worse, in this case, The position where the array can be used is much smaller than the length of the array, which means that the collision probability is further increased;

2. Dynamic expansion of array
With the increase of the number of elements in HashMap, when the array capacity reaches a critical value, it needs to be dynamically expanded.

Load factor (static final float DEFAULT_LOAD_FACTOR = 0.75f;) The main purpose of is to confirm whether the table array needs dynamic expansion. The default value is 0.75. For example, when the size of the table array is 16 and the loading factor is 0.75, the critical value is 12, that is, when the actual size of the table exceeds 12, the table needs dynamic expansion.

During capacity expansion, the resize() method will be called to double the table length (note that the table length is not the critical value).

Splitting of HashMap array expansion elements

The most direct problem in the expansion of HasMap array is to split the elements into a new array. In the process of splitting elements, the hash value needs to be recalculated in JDK7, but it has been optimized in JDK8. Instead of recalculating the hash value, the position of elements in the new array is determined by whether (e.hash & oldcap) is equal to 0.

• When equal to 0, the value of the index position remains unchanged, that is, the index position in the new array is equal to its index position in the old array. We record it as a low linked list area (beginning with lo - low)
• When not equal to 0, the value of the index position is equal to its index position in the old array plus the length of the old array. We record it as a high linked list area (beginning with high - high)

1. Derivation and analysis of (e.hash & oldcap) algorithm

• Pre knowledge:
  a. e.hash represents the hash value of the node element, which is calculated according to the hashCode value of the key.

  b. oldCap is the array length of the old array and is an integer to the nth power of 2. Then its binary representation is 1 1 followed by n 0, such as 1000... 00; And after the integer - 1 to the nth power of 2, its binary representation is n 1s, such as:... 1111.

  c. If you want the result of e.hash & oldCap to be 0, the binary representation of e.hash must be 0 with the position of 1 in the binary of the corresponding oldCap, and other positions can be 0 or 1.

  d. If you want the result of e.hash & oldCap not to be 0, the binary representation of e.hash must be 1 in the binary of the corresponding oldCap, and other positions can be 0 or 1.

• Derivation (e.hash & oldcap) = = 0
  a. We make the following calculation examples
  

  b. We know that the binary representation of the array length - 1 (that is, the integer - 1 to the nth power of 2) is n 1s
  
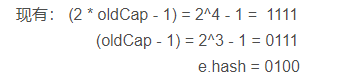
  Therefore, calculate the index position of elements in the array through (array length - 1) & e.hash. The results are as follows:
          
  It can be seen from the above calculation that only the lower 3 bits can really affect the calculation result (because only the lower 3 bits of e.hash are significant bits). But the lower three bits of both are exactly the same, both are 1. Therefore, (2 * oldCap - 1) and (oldCap - 1) have the same results as E. hash after the & operation.

  c. To sum up, it can be concluded that when (e.hash & oldcap) = = 0, the index position of element E in the old and new arrays remains unchanged

• Derivation (e.hash & oldcap)= 0
  a. We make the following calculation examples
  

  b. We know that the binary representation of the array length - 1 (that is, the integer - 1 to the nth power of 2) is n 1s
  
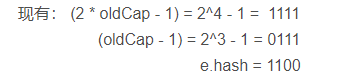
  Therefore, the result of calculating the index position of elements in the array by (array length - 1) & e.hash is as follows:
          
  It can also be seen from the above calculation that only the fourth bit from low to high can really affect the calculation result (because the lower three bits of the binary of (2 * oldCap - 1) and (oldCap - 1) are exactly the same and are all 1). Therefore, (2 * oldCap - 1) and (oldCap - 1) are different from the results of e.hash after & operation.
  c. To sum up, we can get (e.hash & oldcap)= 0, the index position of element E in the new array is equal to its index position in the old array + the length of the old array

Execution flow of put method in HashMap

The put < K, V > method is the core method in HashMap. In the put < K, V > method, HashMap needs to undergo initialization, value storage, capacity expansion, conflict resolution and other operations. The process is complex but the design is exquisite, so it often appears in Java interviews. Let's sort out the core process of put < K, V > method from the macro level, and ignore the more details.

1. Core process steps:

1. First, hash the key and calculate the hash value;
2. Check whether the array table is empty. If it is empty, perform a resize() operation to initialize an array;
3. Calculate the index position of the key in the array according to the hash value;
4. If the location value specified by the index is empty, a new k-v node will be created;
5. If the location value specified by the index is not empty, it indicates that the element of the location already exists, that is, a "hash conflict" occurs;
   5.1 judge whether the key is equal to the first element in the index position. If the key is equal, it indicates that the key already exists. Carry out value overwrite operation. If it is not equal, subsequent judgment is required;
   5.2 judge whether the element at the index position is a treeNode. If so, you need to insert the key into the red black tree;
   5.3 if it is judged that the element at the index position is not a treeNode, it means that the linked list structure is stored here. When traversing the linked list and there is no element equal to the key in the linked list, a new k-v node is created and inserted into the tail of the linked list;
   5.4 after inserting elements, if the length of the linked list is greater than or equal to 8, treeifyBin() will be called to convert the linked list into a red black tree. Note that if the length of the array is less than 64, it will only expand the capacity and will not be converted to a red black tree;
6. After the insert action is completed, the size of the HashMap will be increased by one, and then judge whether the current capacity exceeds the threshold. If it exceeds the threshold, the capacity will be expanded;
7. In the capacity expansion operation, a new array twice as large will be created and the elements in the original array will be split into the new array. Note that if the node elements in the red black tree are less than or equal to 6 during splitting, the red black tree will be converted into a linked list.

2. Put < K, V > method flow chart:
According to the process steps analyzed above, a flow chart is sorted out for everyone to understand.

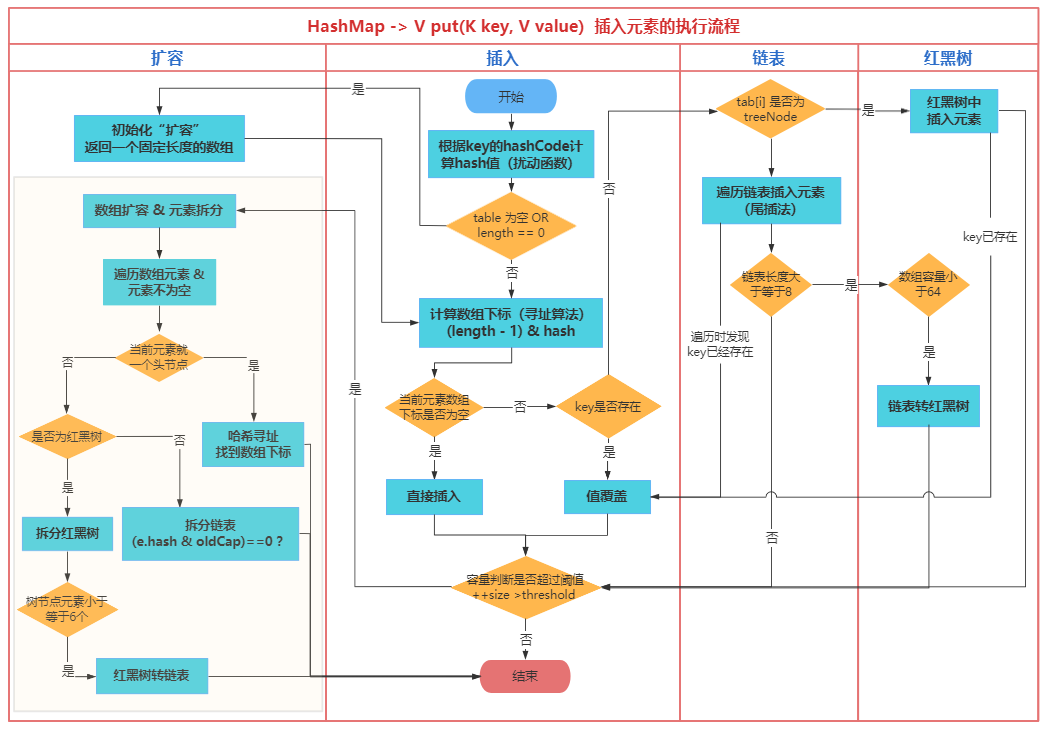
(end)