1. Underlying data structure of HashMap
The bottom layer of HashMap is array + linked list. After 1.8, red and black trees are introduced.
1. Data structure
Array: for using subscript to find elements in the array, the time complexity is O(1); To find through the given value, you need to traverse the array and compare the given keywords and array elements one by one. The time complexity is O(n). For general insert and delete operations, it involves the movement of array elements, and its average complexity is also O(n)
Linear linked list: for operations such as adding and deleting a linked list (after finding the specified operation location), only the references between nodes need to be processed, and the time complexity is O(1), while the search operation needs to traverse the linked list for comparison one by one, and the complexity is O(n)
**Hash table: * * compared with the above data structures, the performance of adding, deleting, searching and other operations in the hash table is very high. Without considering hash conflict, it can be completed only by one positioning, and the time complexity is O(1)
2. Parse hash table
If an array is given a subscript, the time complexity is O(1), so the backbone of the hash table is the array. We want to add or find an element. We can complete the operation by mapping the keyword of the current element to a position in the array through a function and locating it once through the array subscript.
Location = hash (keyword)
Among them, the design of hash function directly affects the overall performance.
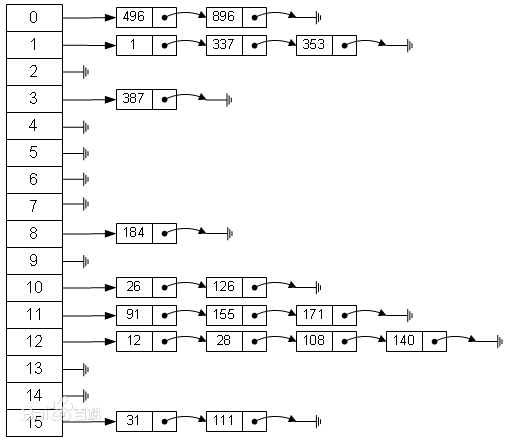
Hash Collisions
In the search process, the number of key code comparisons depends on the number of conflicts. If there are few conflicts, the search efficiency will be high, and if there are many conflicts, the search efficiency will be low. Therefore, the factors that affect the number of conflicts, that is, the factors that affect the search efficiency. There are three factors that affect conflict:
- Whether the hash function is uniform;
- Methods of dealing with conflicts;
- The loading factor of the hash table.
Conflict resolution
The conflict must be solved. At present, the general schemes include open addressing method (in case of conflict, continue to find the next unoccupied storage address), hash function method and chain address method. HashMap adopts the chain address method, that is, array + linked list
2. Implementation principle of HashMap
1. HashMap structure
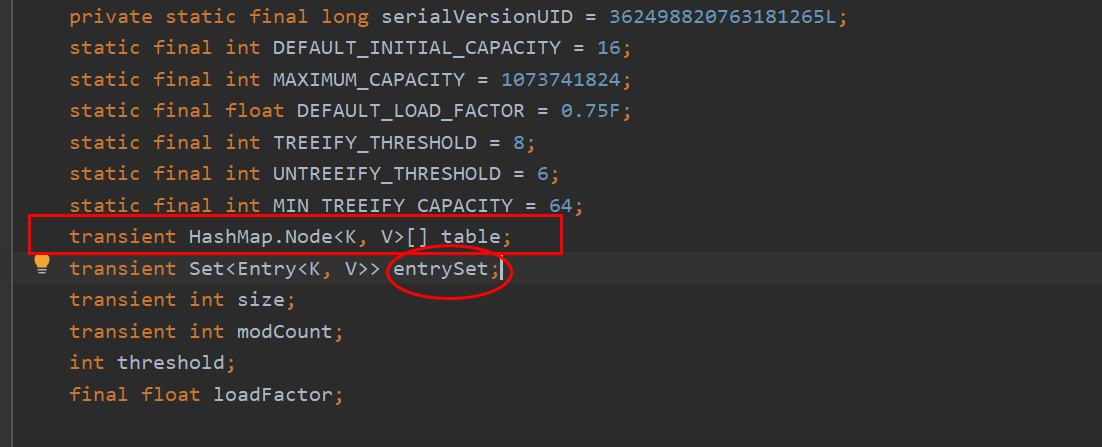
The backbone of HashMap is an entry array. Entry is the basic unit of HashMap. Each entry contains a key value pair.
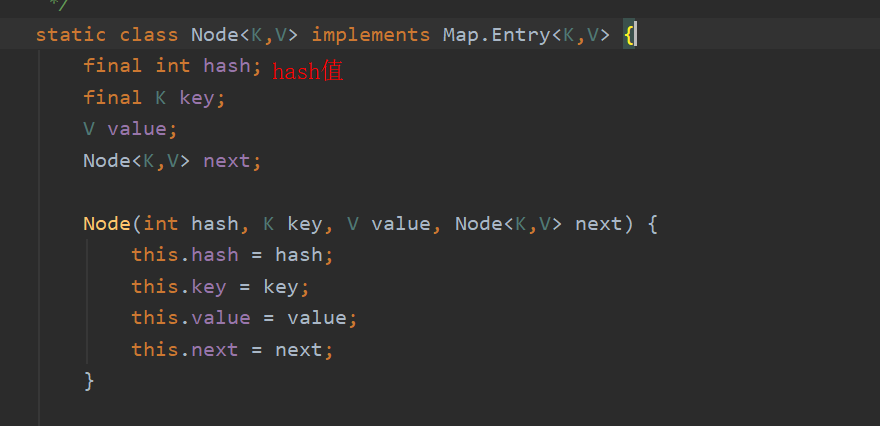
Hash is the hash value of an int that operates on the Key, and next points to the next Node, so we can infer that the general structure of HashMap should be like this.
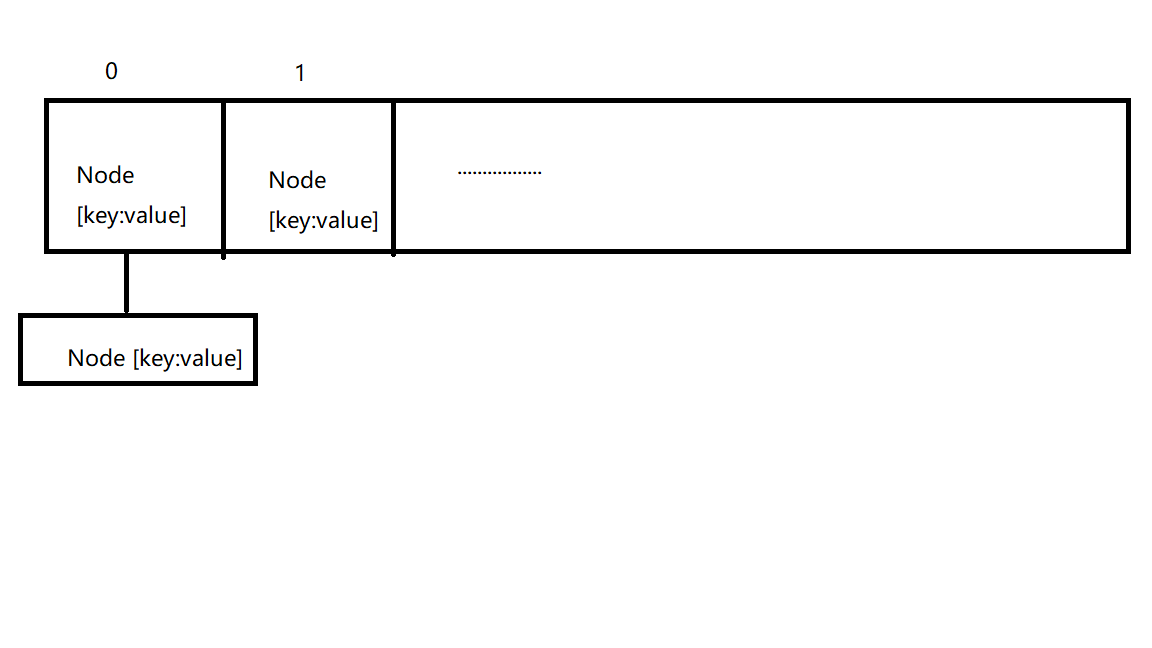
In short, HashMap is composed of array + linked list. Array is the main body of HashMap, and linked list mainly exists to solve hash conflicts, If the location of the located array does not contain a linked list (the next of the current entry points to null), the operations such as finding and adding are fast and only need to be addressed once; if the location of the array contains a linked list, the time complexity of the addition operation is O(n). First traverse the linked list and overwrite it if it exists, otherwise add it; For the search operation, you still need to traverse the linked list, and then compare and search one by one through the equals method of the key object. Therefore, in consideration of performance, the fewer linked lists in HashMap appear, the better the performance will be.
2. Other parameters of HashMap
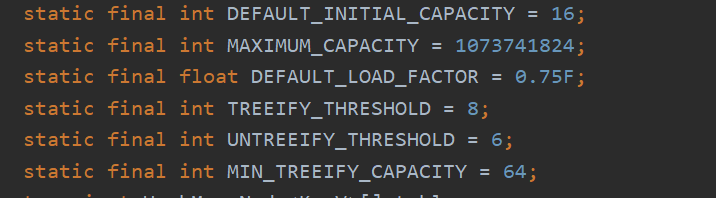
Default initial length 16
The load factor represents the filling degree of the table. The default is 0.75
HashMap has four constructors. If the user does not pass in two parameters, initialCapacity and loadFactor, the default value will be used. InitialCapacity is 16 by default and loadFactory is 0.75 by default. If it is not an incoming map,HashMap will not actively allocate memory space. Instead, the table array is actually built when the put operation is performed
3. put method
public V put(K var1, V var2) {
return this.putVal(hash(var1), var1, var2, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
The initialization array table [] in HashMap is a lazy loading mode
If the table is null, initialize the table array through the resize() method, which is also a capacity expansion method
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
It is mainly used to determine the type of current operation (initialization or expansion) and calculate the capacity and threshold of the newly generated table.
Threshold indicates that the resize operation will be performed when the size of the HashMap is greater than threshold.
threshold=capacity*loadFactor
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
}
If the value node calculated through hash is null, a new node node is initialized through newNode, and then the value is put into the corresponding array
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
If the array calculated by hash is not empty, that is, table [[i = (n - 1) & hash] is not empty.
Then judge whether the key of the node is the same as the key we will save. If it is the same, obtain the node, that is, e=p
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
If the key of the node is not equal to ours, it depends on whether the node is a red black tree or a linked list. If it is a red black tree, the key value is saved in the red black tree through the red black tree
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
If it is a linked list, the tail insertion method is used to insert the node. If it is greater than 8, the node becomes a red black tree. But this is not entirely correct. Look at this:
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
If the length of the array is less than 64, expand the capacity, otherwise turn the linked list into a red black tree
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
If e is not equal to null, it means that there is the same key in the HashMap as the one we are about to save. Then replace the value in the node, that is, e.value=value, and put back the old value
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
modCount is the number of times we modify the HashMap to quickly fail, that is, fast fail
threshold=capacity * loadfactor, i.e. array initialization length * load factor, if
this.loadFactor = DEFAULT_LOAD_FACTOR; DEFAULT_LOAD_FACTOR=0.75
If the data stored in the HashMap is greater than three-quarters of the array length, it needs to be expanded
3. Test verification
1. Postscript
Truth always needs to be practiced, so we actually use breakpoints to verify it.

Get the hash value key value
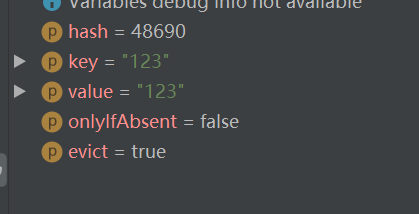

This verifies that it is lazy loading and resize s when put

Create a new node

Insert the same key the second time
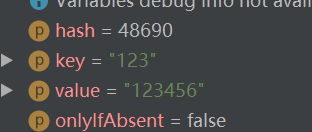
We will find that the hash value calculated by him is the same, so

Needless to say, the key is the same.

The old value is replaced by the new value. The whole process of put is completed