HashMap principle and source code analysis
1. Storage structure
HashMap is implemented internally by an array of node types. Node contains key value pairs and has four internal fields. We can see from the next field that node is a linked list. That is, each position of the array is treated as a bucket, and each bucket stores a linked list. HashMap uses the zipper method to solve conflicts. Nodes with the same hashcode and array length modulo operation results are stored in the same bucket.
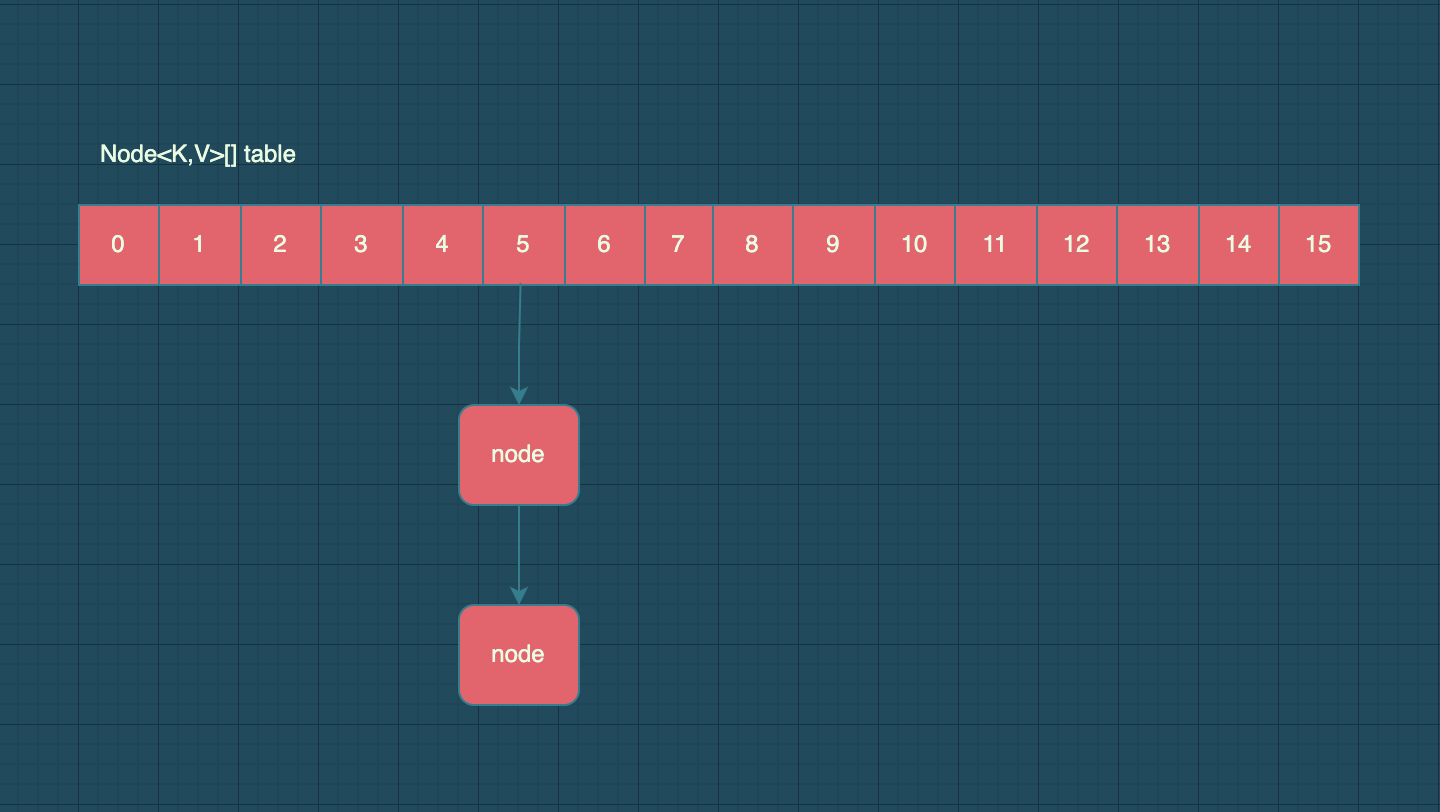
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
2. Index calculation
In HashMap, the index of node in the array is obtained by modular operation according to the hash value of key and the length of the array.
The following is the actual execution process of putVal method (put method) in HashMap,
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
// ...
}
You can see in line 6
i = (n - 1) & hash
Where i is the index calculated according to the key, and n is the size of the array.
This is because in HashMap, if the size of the array is \ (2^n \), its binary form has the following characteristics:
Let x = 1 < < 4, that is, X is the 4th power of 2
x : 0001 0000 x-1 : 0000 1111
Sum a number y and x - 1
y : 1101 1011 x-1 : 0000 1111 y&(x-1) : 0000 1011
This property is the same as y's modulus effect on x
y : 1101 1011 x : 0001 0000 y%x : 0000 1011
We know that the cost of bit operation is much lower than modular operation, so using bit operation can bring higher performance.
3. put operation
The put method in HashMap actually executes the putVal method.
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
The following is the implementation of putVal method. In order to better understand the put operation, the red black tree and capacity expansion in the source code are replaced by ellipsis.
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// When the map is just constructed and no elements are added, the array is null and needs to be initialized
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// Calculate the index. If the bucket at the index position is empty, put it into the bucket
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
// If the key of the bucket head node is the same as the key to be inserted, assign it to e (E is the node to be updated)
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// ...
else {
// Traverse the linked list in the bucket
for (int binCount = 0; ; ++binCount) {
// If you reach the tail of the linked list, that is, there is no node of the key in the map, you will add it to the tail
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
// ...
break;
}
// If a key exists during traversal, it is assigned to e
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// e is not empty, indicating that the key exists in the map. Update its value
if (e != null) {
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
//...
}
summary
The main steps of put operation are:
- Calculate the index of node in the array according to the key
- If the index position is empty, put node into the index position
- If not empty
- Traverse the elements in the bucket at the index position, compare whether the key of the element in the bucket is the same as the key, and update its value if it is the same
- If the key does not exist in the bucket, create a new node and put it into the bucket
4. Capacity expansion
Let the length of the array in the HashMap be n and the number of stored key value pairs be m. on the premise that the hash function meets the uniformity, the length of each linked list is m / n. Therefore, the time complexity of the lookup is O(m / n).
In order to reduce the search efficiency, that is, reduce m / n, you should increase n, that is, the length of the array. HashMap uses dynamic capacity expansion to adjust the size of the array according to the number of current key value pairs, so that both space and time efficiency can be guaranteed.
Parameters related to capacity expansion mainly include capacity, size, threshold and loadFactor
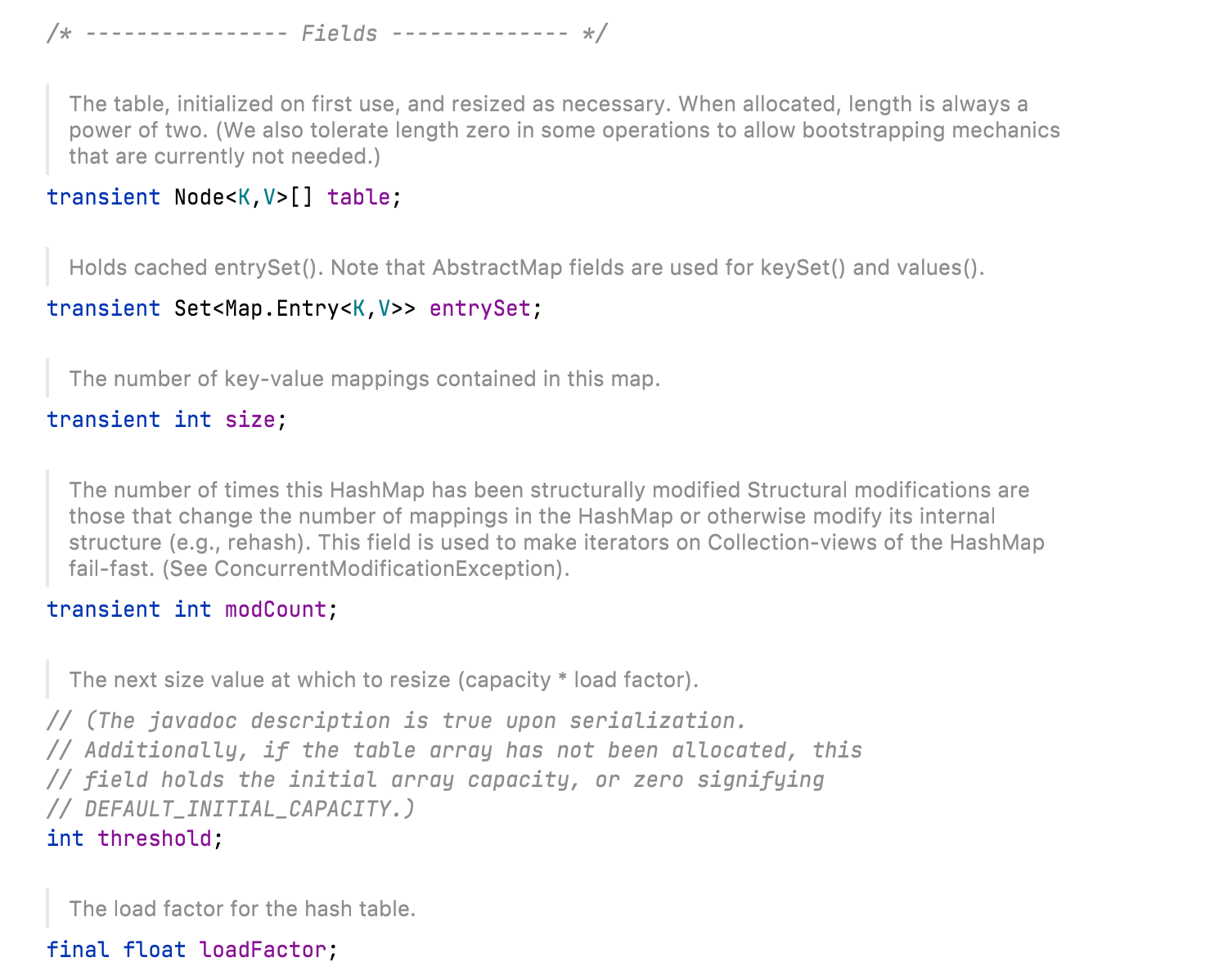
| parameter | meaning |
|---|---|
| capacity | The size of the table array. The default is 16 |
| size | Number of key value pairs |
| threshold | The critical value of size. When size is greater than the threshold, capacity expansion must be performed |
| loadFactor | Load factor, which is 0.75 by default. threshold = (int) (capacity * loadFactor) |
The capacity expansion operation is triggered in putVal under two conditions
- At the beginning of the map, the array size is 0 and needs to be expanded
- When the number of key value pairs exceeds the critical value, capacity expansion is triggered
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length; /* The array is null and needs to be expanded */
// ...
if (++size > threshold)
resize(); /* size If the critical value is exceeded, the capacity expansion is triggered */
// ...
}
Capacity expansion is mainly divided into two steps
- Expand the capacity of the array
- After capacity expansion, all keys of the original array need to be inserted into the new array
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
// 1. Capacity expansion
if (oldCap > 0) {
// If the capacity is greater than or equal to the maximum capacity, the capacity cannot be expanded. Change the critical value to the maximum value of int and return (because there is no capacity expansion, there is no need to re insert the key)
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// Expand the capacity to twice the original capacity and modify the critical value to twice the original capacity
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1;
}
else if (oldThr > 0) // If the array size is 0 and the critical value is not 0, the initial size of the array is the critical value (the tableSizeFor method ensures that the oldThr is the nth power of 2, as described in the next section)
newCap = oldThr;
else { // If the array size is 0 and the critical value is 0, the initial size is 16 and the initial critical value = 0.75 * 16 = 12
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
// 2. Reinsert the key
if (oldTab != null) {
// Traverse old arrays
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
// If the bucket contains elements, the elements in the bucket are traversed
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
// If there is only one element in the bucket, just recalculate the index
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
// If there are red and black trees in the bucket
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // Traversal linked list
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
/**
* for instance
* oldCap : 0001 0000
* newCap : 0010 0000
* newCap-1: 0001 1111
* If the hash and old array size sum operation is 0, it indicates
* When hashing with newCap-1, it operates with the highest bit 1
* If the result is 0, the index position is at [0,oldCap)
* If the operation result is not 0, the index position is [oldCap, newCap)
* In the same bucket, the operation result is the same as oldCap-1,
* That is, for elements in the same bucket, the calculated new index is either the old index value,
* Either the old index value + oldCap (with the highest 1 and not 0)
* Then loHead is the head node of the old index location, and hiHead is
* The head node at the new index location
*/
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
5. Ensure that the array capacity is \ (2^n \)
The constructor of HashMap allows the user to pass in the initial capacity, and may not be \ (2^n \). However, HashMap can convert it to \ (2^n \).
First consider how to find the mask of a number. For 1000 0000, its mask is 1111 1111. The following methods can be used:
mask |= mask >> 1 1100 0000 mask |= mask >> 2 1111 0000 mask |= mask >> 4 1111 1111
Then mask + 1 is the nth power greater than the smallest 2 of the original number

HashMap ensures that the array capacity is to the nth power of 2 through tableSizeFor
