catalogue
preface
The principle of bubble sorting, selection sorting and merging sorting algorithms is reprinted. Their description and introduction are illustrated with pictures and text, which is better than my recount. Therefore, some of the better contents of the introduction are reprinted, and the address of the original content has been indicated. The algorithm is implemented in C language, which is simpler and clearer. I hope this blog will let you understand the seven sorting algorithms at one time. It's not easy to be original. Praise and support readers!
Seven sort Preview
|
Sorting algorithm
|
Average time complexity
|
Best case
|
Worst case scenario
|
sort order
|
stability
|
|
Bubble sorting
| O(n * n) |
O(n)
|
O(n * n)
|
In-place
|
stable
|
|
Select sort
|
O(n * n)
|
O(n * n)
|
O(n * n)
|
In-place
|
In-place
|
|
Insert sort
|
O(n * n)
|
O(n)
|
O(n * n)
|
In-place
| stable |
|
Shell Sort
|
O(n * log n)
|
O(n * log n)
|
O(n * log n)
|
In-place
|
instable
|
|
Merge sort
|
O(n * log n)
|
O(n * log n)
|
O(n * log n)
|
Out-place
| stable |
|
Heap sort
|
O(n * log n)
|
O(n * log n)
|
O(n * log n)
| In-place |
instable
|
|
Quick sort
|
O(n * log n)
|
O(n * log n)
|
O(n * n)
| In-place |
instable
|
Bubble sorting
This block of content is reproduced from the blog park. The original code is described in java. I use C language to describe it below. Original address: Three minutes to thoroughly understand bubble sorting
Bubble sort: If equal values are not exchanged, this sort method is a stable sort method.
1. Principle: compare two adjacent elements and exchange the elements with large values to the right
2. Idea: compare the two adjacent numbers in turn, put the smaller number in the front and the larger number in the back.
(1) first comparison: first compare the first and second numbers, put the decimal in front and the large number in the back.
(2) compare the 2nd and 3rd numbers and put the decimal number in front and the large number in the back.
......
(3) continue in this way until the last two numbers are compared, put the decimal number in the front and the large number in the back, and repeat the steps until all sorting is completed
(4) after the above comparison, the last number must be the largest number in the array, so the last number will not participate in the comparison during the second comparison.
(5) after the second comparison, the penultimate number must also be the penultimate number in the array, so in the third comparison, the last two numbers do not participate in the comparison.
(6) by analogy, the number of comparisons per trip is reduced
3. Examples:
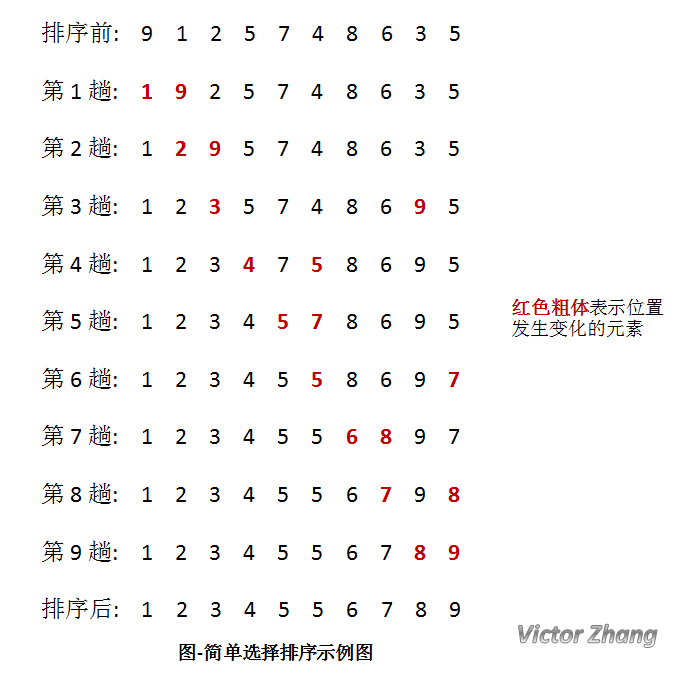
(1) array to sort: [10,1,35,61,89,36,55]
(2) first sequence:
First sorting: compare 10 with 1, 10 is greater than 1, exchange position [1,10,35,61,89,36,55]
The second sequence: compare 10 and 35. If 10 is less than 35, the position will not be exchanged [1,10,35,61,89,36,55]
The third sequence: 35 is compared with 61, 35 is less than 61, and the position is not exchanged [1,10,35,61,89,36,55]
The fourth sequence: 61 is compared with 89, 61 is less than 89, and the position is not exchanged [1,10,35,61,89,36,55]
The fifth sequence: comparison between 89 and 36, 89 is greater than 36, exchange position [1,10,35,61,36,89,55]
The sixth sequence: comparison between 89 and 55, 89 greater than 55, exchange position [1,10,35,61,36,55,89]
A total of six comparisons were made in the first trip, and the sorting results: [1,10,35,61,36,55,89]

(3) the second sequence:
The first sorting: 1 is compared with 10, 1 is less than 10, and positions 1, 10, 35, 61, 36, 55, 89 are not exchanged
Second ranking: compare 10 and 35, 10 is less than 35, and do not exchange positions 1,10,35,61,36,55,89
The third ranking: 35 is compared with 61, 35 is less than 61, and positions 1,10,35,61,36,55,89 are not exchanged
The fourth sorting: 61 and 36 are compared, 61 is greater than 36, and the exchange positions are 1,10,35,36,61,55,89
The fifth sorting: 61 and 55 are compared, 61 is greater than 55, and the exchange positions are 1,10,35,36,55,61,89
A total of 5 comparisons were made in the second trip, and the sorting results were 1,10,35,36,55,61,89
(4) the third sequence:
Compared with 1 and 10, 1 is less than 10, and positions 1, 10, 35, 36, 55, 61, 89 are not exchanged
The second ranking: compare 10 and 35, 10 is less than 35, and do not exchange positions 1,10,35,36,55,61,89
The third ranking: 35 is compared with 36, 35 is less than 36, and positions 1,10,35,36,55,61,89 are not exchanged
The fourth sorting: 36 is compared with 61, 36 is less than 61, and positions 1,10,35,36,55,61,89 are not exchanged
A total of 4 comparisons were conducted in the third trip, and the sorting results were 1,10,35,36,55,61,89
So far, the position has been in an orderly situation.
4. Algorithm analysis:
(1) it can be seen that N numbers need to be sorted, and a total of N-1 times are sorted. The sorting times of each I time is (N-i). Therefore, double loop statements can be used. The outer layer controls the number of cycles, and the inner layer controls the number of cycles per trip
(2) advantages of bubble sorting: each time you sort, you will compare it less, because each time you sort, you will find a larger value. For example, after the first comparison, the last number must be the largest number. During the second sorting, you only need to compare the numbers other than the last number. Similarly, you can find the largest number behind the numbers participating in the second comparison. During the third comparison, you only need to compare the numbers other than the last two numbers, And so on... That is to say, there is no comparison, and each comparison is less, which reduces the amount of algorithm to a certain extent.
(3) time complexity
1. If our data is in positive order, we only need to go once to complete the sorting. The required comparison times C and recording movement times M reach the minimum value, that is, Cmin=n-1;Mmin=0; Therefore, the best time complexity of bubble sorting is O(n).
2. If unfortunately our data is in reverse order, we need to sort n-1 times. n-i comparisons (1 ≤ I ≤ n-1) shall be made for each sequence, and each comparison must move the record three times to reach the exchange record position. In this case, the number of comparisons and moves reaches the maximum:
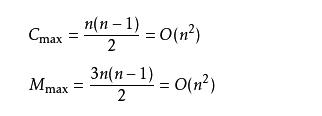
To sum up, the total average time complexity of bubble sorting is O(n2), and the time complexity is independent of the data status.
5.C language code implementation
#include <stdio.h>
void BubbleSort(int arr[],int len)
{
if (len < 1 || arr==nullptr) return;
for(int i=0;i<len;i++)
for (int j=0; j < len-i-1; j++)
{
if (arr[j]> arr[j + 1])
{
int temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}
void PrintAddr(int arr[], int len)
{
for (int i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main()
{
int arr[] = { 10,1,35,61,89,36,55};
int len = sizeof(arr) / sizeof(arr[0]);
BubbleSort(arr, len);
PrintAddr(arr, len);
}Select sort
This block of content is reproduced from the blog park. The original code is described in java. I use C language to describe it below. Original address: Simple selection sort
Simple selection sort is a kind of selection sort.
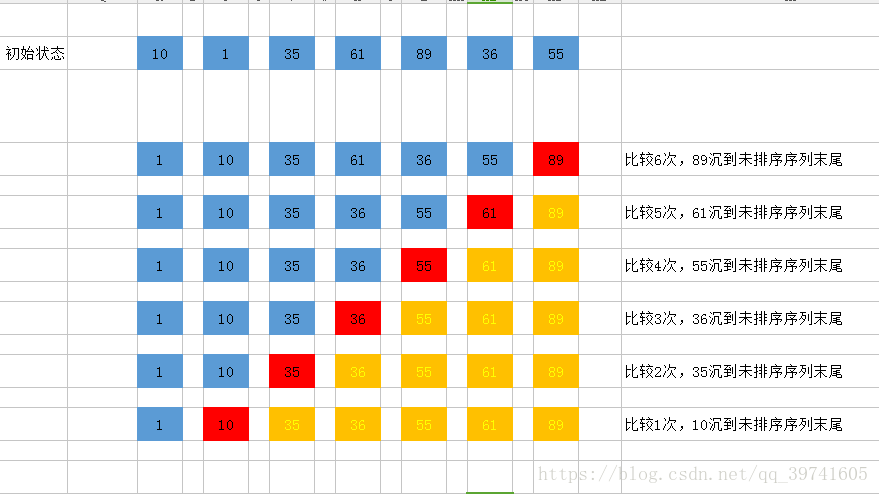
Select Sorting: select the record with the smallest keyword from the records to be sorted each time, and place the order at the end of the sorted record sequence until the end of all sorting.
Simple sort processing flow
(1) Find the element with the smallest keyword from the sequence to be sorted;
(2) If the smallest element is not the first element of the sequence to be sorted, exchange it with the first element;
(3) From the remaining N - 1 elements, find the element with the smallest keyword and repeat steps (1) and (2) until the sorting is completed.
As shown in the figure, in each sorting, the element with the smallest current ^ i ^ is placed at position ^ i ^.
Time complexity
The comparison times of simple selection sorting are independent of the initial sorting of the sequence. Assuming that the sequence to be sorted has N} elements, the comparison times are always N (N - 1) / 2.
The number of moves is related to the initial sorting of the sequence. When the sequence is in positive order, the number of moves is the least, which is ﹤ 0
When the sequence is in reverse order, the maximum number of moves is 3N (N - 1) / 2.
Therefore, based on the above, the time complexity of simple sorting is O(N2).
C language code implementation
#include <stdio.h>
void SelectSort(int arr[], int len)
{
if (len < 1 || arr == nullptr) return;
for (int i = 0; i < len; i++)
{
int index = i;//The index used to hold the minimum value
for (int j = i + 1; j < len; j++)
{
if (arr[j] < arr[index])
{
index = j;
}
}
int temp = arr[i];
arr[i] = arr[index];
arr[index] = temp;
}
}
void PrintAddr(int arr[], int len)
{
for (int i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main()
{
int arr[] = { 9,1,2,5,7,4,8,6,3,5 };
int len = sizeof(arr) / sizeof(arr[0]);
SelectSort(arr, len);
PrintAddr(arr, len);
}
Insert sort
#include <stdio.h>
void InsertSort(int arr[], int len)
{
for (int i = 1; i < len; i++)
{
int curVaule = arr[i];
int preIndex = i - 1;
while (preIndex >= 0 && arr[preIndex] > curVaule)
{
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = curVaule;
}
}
void PrintAddr(int arr[], int len)
{
for (int i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main()
{
int arr[] = { 171,161,163,165,167,169 };
int len = sizeof(arr) / sizeof(arr[0]);
InsertSort(arr, len);
PrintAddr(arr, len);
}
Shell Sort
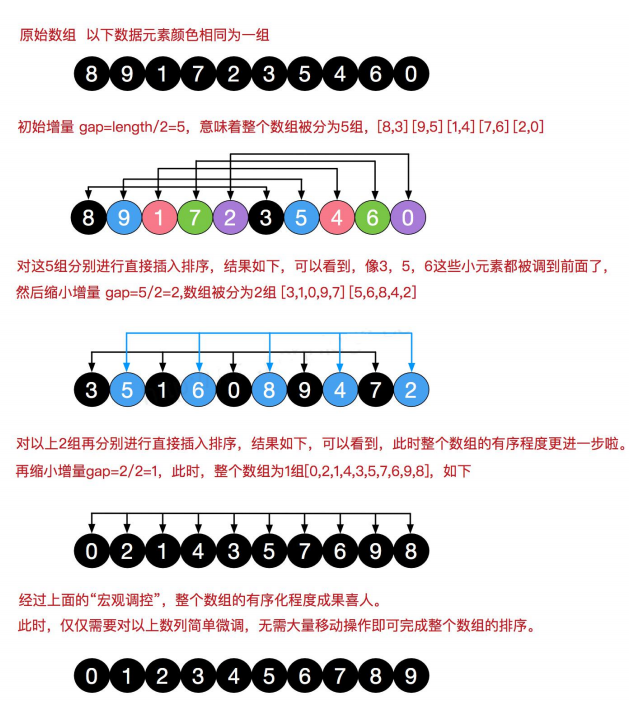
C language code implementation
#include<stdio.h>
void ShellSort(int arr[], int len)
{
for (int gap = len / 2; gap > 0; gap /= 2)
{
for (int i = gap; i<len; i++)
{
int curValue = arr[i];
int preIndex = i - gap;
while (preIndex >= 0 && arr[preIndex] > curValue)
{
arr[preIndex + gap] = arr[preIndex];
preIndex -= gap;
}
arr[preIndex + gap] = curValue;
}
}
}
void PrintAddr(int arr[], int len)
{
for (int i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main()
{
int arr[] = { 8,9,1,7,2,3,5,4,6,0 };
int len = sizeof(arr) / sizeof(arr[0]);
ShellSort(arr, len);
PrintAddr(arr, len);
}
Merge sort
This block of content is reproduced from the blog park. The original code is described in java. I use C language to describe it below. Original address: Graphic sorting
Merge sort is a sort method based on the idea of merging. The algorithm adopts the classical divide and conquer strategy (divide and conquer divides the problem into some small problems and then solves them recursively, while the conquer stage "fixes" the answers obtained in the stages, that is, divide and conquer).
(if it is difficult to understand the idea of divide and conquer algorithm, you can move to my blog: ❤️ "Disgusting work" a blog takes you to master the "five core algorithms" ❤️)
divide and rule
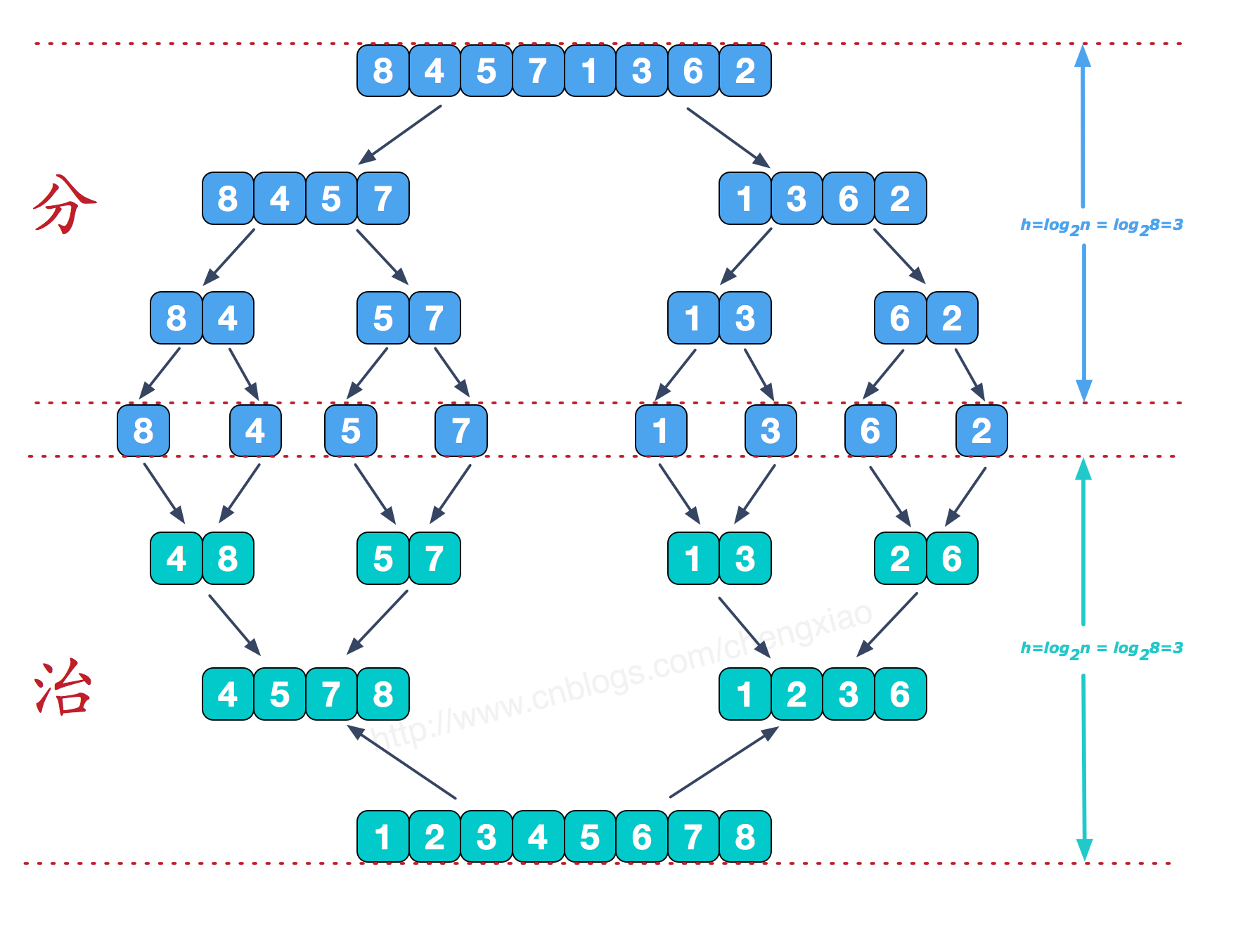
It can be seen that this structure is very similar to a complete binary tree. The merging and sorting in this paper is realized recursively (or iteratively). The stage can be understood as the process of recursively dismantling molecular sequences, and the recursion depth is log2n.
Merge adjacent ordered subsequences
Let's take another look at the treatment stage. We need to merge two ordered subsequences into one ordered sequence. For example, in the last merging in the figure above, we need to merge two ordered subsequences [4,5,7,8] and [1,2,3,6] into the final sequence [1,2,3,4,5,6,7,8]. Let's see the next implementation steps.
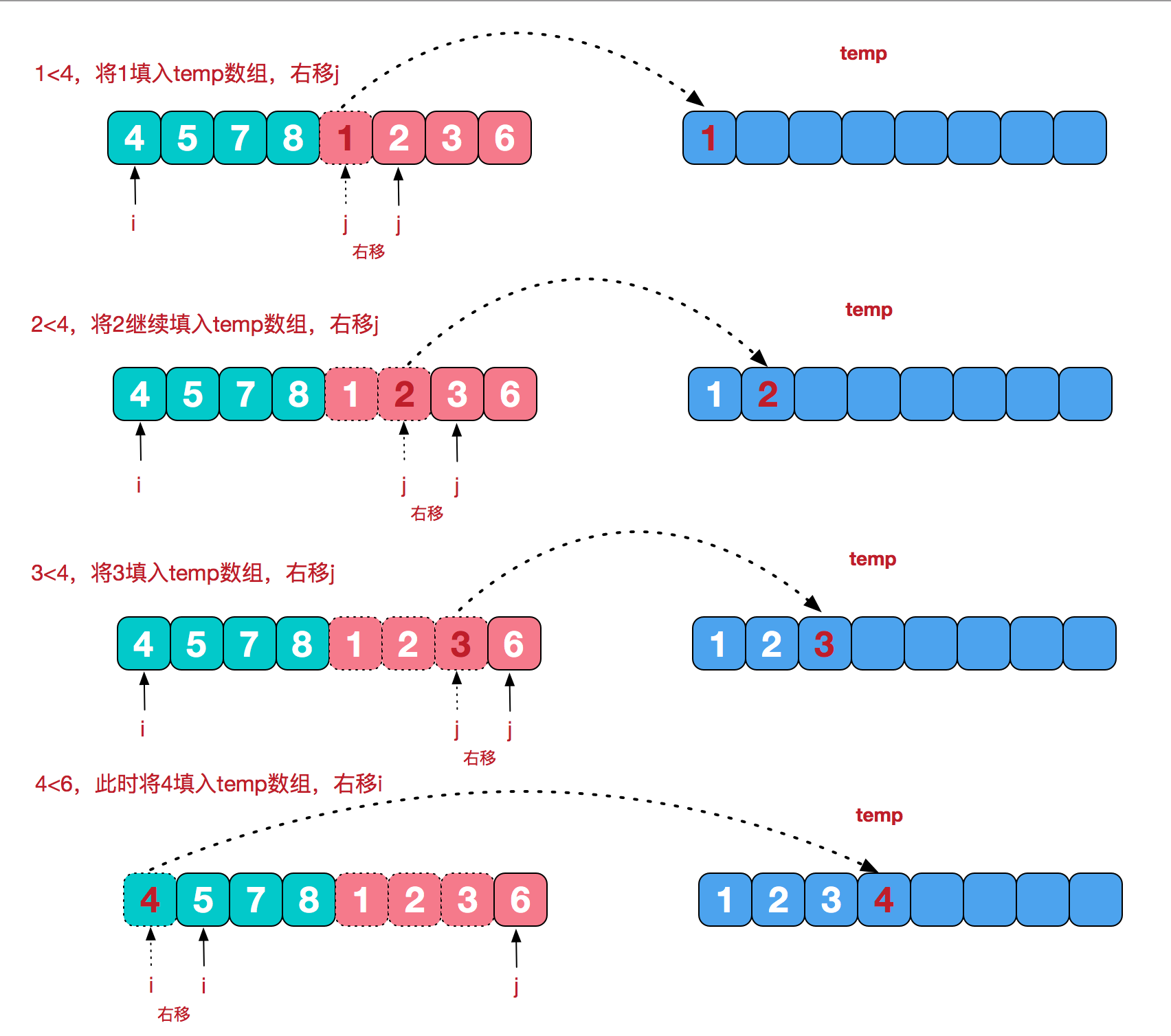
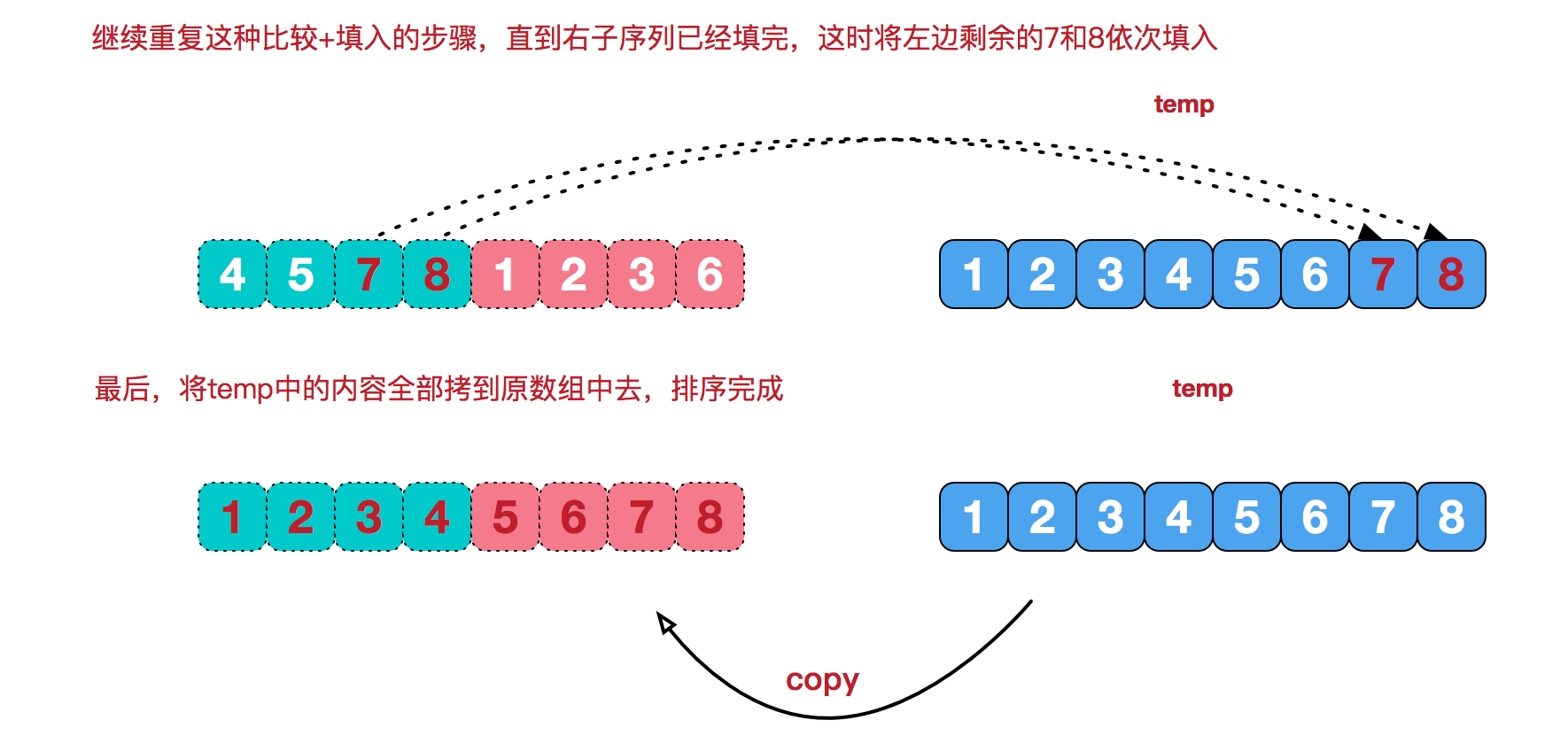
C language code implementation
#include <stdio.h>
#include<string.h>
void MergeAdd(int arr[], int left, int mid, int right, int *temp)
{
int lmin = left;
int rmin = mid;
int index = left;
while (lmin<mid && rmin<=right)
{
if (arr[lmin] < arr[rmin])
{
temp[index++] = arr[lmin++];
}
else
{
temp[index++] = arr[rmin++];
}
}
while (lmin < mid)
temp[index++] = arr[lmin++];
while (rmin <= right)
temp[index++] = arr[rmin++];
memcpy(arr + left, temp + left, sizeof(int)*(right - left + 1));
}
void MergeSort(int arr[], int left, int right, int *temp)
{
if (left <0 || arr == nullptr) return;
if (left < right)
{
int mid = (right+left)/2;
MergeSort(arr, left, mid, temp);
MergeSort(arr, mid+1, right, temp);
MergeAdd(arr, left, mid + 1, right, temp);
}
}
void PrintAddr(int arr[], int len)
{
for (int i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main()
{
int arr[] = { 8,9,1,7,2,3,5,4,6,0 };
int len = sizeof(arr) / sizeof(arr[0]);
int *temp = new int[len];
MergeSort(arr,0,len-1,temp);
PrintAddr(arr, len);
delete temp;
}
Heap sort
For a detailed introduction to the data structure and algorithm implementation of heap, please move to my blog Definition, attributes and algorithm implementation of data structure heap , only heap sorting algorithm is introduced here
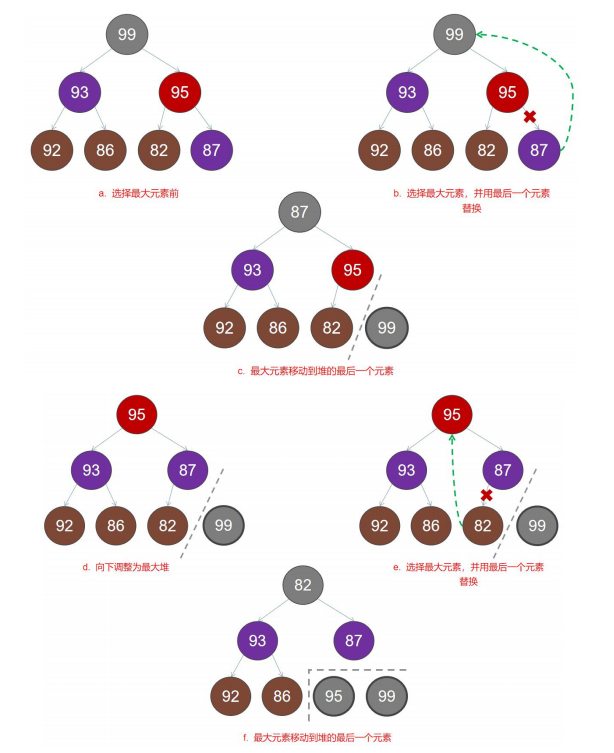
stay Definition, attributes and algorithm implementation of data structure heap On the premise of blog introduction, the implementation code of heap sorting C language is as follows:
void HeapSort(int *_arr,int size)
{
int capacity = DEFAULT_CAPACITY > size ? DEFAULT_CAPACITY : size;
Heap heap;
heap.arr = _arr;
heap.size = 0;
if(size>0)
{
heap.size = size;
buildHeap(heap);
}
while (heap.size > 0)
{
int tmp = heap.arr[0];
heap.arr[0] = heap.arr[heap.size-1];
heap.arr[heap.size - 1] = tmp;
heap.size--;
adjustDown(heap, 0);
}
}Quick sort


#include <stdio.h>
int partition(int arr[], int low, int high)
{
int i = low;
int j = high;
int base = arr[low];
if (low < high)
{
while (i < j)
{
while (i < j && arr[j] >= base)
{
j--;
}
if (i < j)//There is a number smaller than the base on the right
{
arr[i++] = arr[j];
}
while (i < j&&arr[i] < base)
{
i++;
}
if (i < j)//There is a number larger than the base on the left
{
arr[j--] = arr[i];
}
}
arr[i] = base;
}
return i;
}
//Quick sort
void QuickSort(int arr[], int low, int high)
{
if (low < high)
{
int index = partition(arr, low, high);
QuickSort(arr, low, index - 1);
QuickSort(arr, index + 1, high);
}
}
void PrintAddr(int arr[], int len)
{
for (int i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
}
int main()
{
int arr[] = { 163, 161, 158, 165, 171, 170, 163, 159, 162 };
int len = sizeof(arr) / sizeof(arr[0]);
QuickSort(arr, 0, len - 1);
PrintAddr(arr, len);
}It's not easy to summarize, one button three times!