1, Heap and related operations

1. Heap structure is a complete binary tree structure implemented by array
   size refers to the number of nodes
   I position, left child 2i+1, right child 2i+2, parent node (i-1)/2 rounded down
2. In a complete binary tree, if the maximum value of each subtree is at the top, it is a large root heap
3. In a complete binary tree, if the minimum value of each subtree is at the top, it is a small root heap
4. heapInsert and heapify operations of heap structure

• (1) Insert operation heapInsert
  Insert the tail and constantly compare O(logN) with the parent node

//A number is now in the index position and continues to move upward
public static void heapInsert(int[] arr,int index){
	while(arr[index] > arr[(index - 1) / 2]){  //The number of index positions > its parent node or has reached the head
		swap(arr,index,(index - 1) / 2);  //exchange
		index = (index - 1) / 2;  //The value of index is transformed to the original parent node
	}
}

• (2) Large root heap maximum operation
  1. First return the maximum value of the large root heap (i.e. the root heapsize)
  2. Put the last node at the root, compare it with the left and right children once, and keep sinking until the left and right children are smaller than it, or there are no children

• (3) Can I move heapify down
  O(logN)

//Can a number move down when it is in the index position
public static void heapify(int[] arr,int index,int heapSize){
	int left = index * 2 + 1; //Left child subscript
	while(left < heapSize){ //When there are children below, if the left child is < size, there must be a right child < size
		//Which of the two children is the most valuable? Give the subscript to large
		int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
		//Between the father and the older child, who is worth more, give the subscript to bigger
		largest = arr[largest] > arr[index] ? largest : index;
		if(largest == index){   //If the maximum value is index compared with children, it will jump out
			break;
		}
		swap(arr,largest,index);  //Otherwise, exchange the values of index and largest
		index = largest;          //index moves down to the position at the maximum value
		left = index * 2 + 1;     //Update left and continue the cycle
	}
}

• (4) Change the value of the i th node
  Large root pile:
  1. If the value of position I becomes smaller = > the heapify operation is performed down from position i
  2. If the value of position I becomes larger = > the heapInsert operation is performed upward at position i

1. Increase and decrease of reactor structure
2. The priority queue structure is the heap structure
   (heap ordering is often less important than heap structure)

PriorityQueue<Integer>heap = new PriorityQueue<>(); //Small root pile

2, Heap sort*

• Time complexity: O(NlogN)
• Space director: O(1)
• Large root pile:
  1. Add the numbers in the sequence one by one and form a large root pile side by side.
  2. Swap the maximum number of positions with the first element and return the maximum number of positions
  3. Repeat the above process and return continuously to get the descending sequence

package com.godzuo.java;
import java.util.Arrays;

public class HeapSort {
    public static void heapSort(int[] arr){
        if(arr == null || arr.length < 2) 
        	return;
//        for(int i = 0;i < arr.length;i++){  //O(N)
//            heapInsert(arr,i);  // Build large root heap O(logN)
//        }

        for(int i = arr.length - 1;i >= 0;i--){  //O(N), the time complexity does not change, but the speed becomes faster, because it is sorted as O(NlogN). If you just become a heap, you should choose this method.
            heapify(arr,i,arr.length);  
        }

        int heapSize = arr.length;
        swap(arr, 0, --heapsize);  //The number at position 0 is exchanged with the number at the last position on the heap, and the size of the heap after exchange--
        while (heapsize > 0) {  //O(N)
            heapify(arr, 0, heapsize); //The number at position 0 goes down and readjusts to large root heap O(logN)
            swap(arr, 0, --heapsize);  //Continue exchange, -- O(1)
        }       
    }
}

    //Build large root pile
    public static void heapInsert(int[] arr,int i){
       while (arr[i]>arr[(i-1)/2]){
            swap(arr,i,(i-1)/2);
            i = (i-1)/2;
       }
    }
    public static void swap(int[] arr,int i,int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    //Modify large root heap
    public static void heapify(int[] arr,int index,int heapSize){
        int left = index*2+1;
        while (left < heapSize){
            int largest = left+1 < heapSize && arr[left+1] > arr[left] ? left+1 : left;
            largest = arr[largest] > arr[index] ? largest : index;
            if (largest == index){
                break;
            }
            swap(arr,largest,index);
            index = largest;
            left = index*2+1;
        }
    }

    public static void main(String[] args) {
        int[] arr = {1,3,2,6,5,9};
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

• improvement:
  Instead of adjusting one after another, all of them will be added to the heapify from right to left.
  

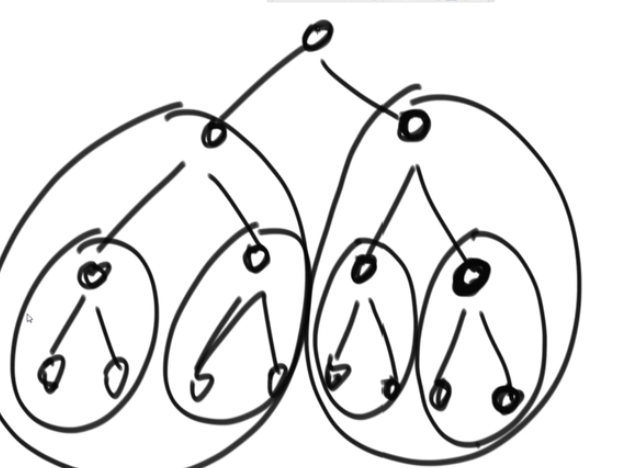
3, Heap sorting problem expansion

[title]
An almost ordered array is known, which means that if the array is arranged in order, each element can move no more than k, and K is relatively small relative to the array. Please select an appropriate sorting algorithm to sort this data.
[analysis]
Time complexity: O (nlock) can be approximately equal to O(N)

public class SortArrayDistanceLessK(int[] arr,int k){
	//Default small root heap
	PriorityQueue<Integer> heap = new PriorityQueue<>();
	int index = 0;
	for(;index <= Math.min(arr.length,k);index++){
		heap.add(arr[index]);   // The first k numbers are arranged in a small root pile
	}
	int i = 0;
	for(;index < arr.length;i++,index++){
		heap.add(arr[index]); //Add a value
		arr[i] = heap.poll(); //Play a value
	}
	while(!heap.isEmpty()){
		arr[i++] = heap.poll;  //Pop up the rest
	}
}

4, Heap structure

//Java default small root heap
PriorityQueue<Integer> heap = new PriorityQueue<>(); 

heap.add(8);
heap.add(4);
heap.add(9);
heap.add(10);
heap.add(3);

while(!heap.isEmpty())
	System.out.println(heap.poll());

1. Capacity expansion
   Expansion times: logN
   Cost per expansion: O(N)
   Total cost of capacity expansion: O(NlogN)
   Average capacity expansion cost: O(NlogN)/N=O(logN)

2. Heap structure of the system
   1. add and poll pop up
   It is convenient, but it does not support the formed heap. After manual value change and other operations, it can be readjusted to heap at a very small cost
   2. Handwritten heap can be implemented efficiently

5, Comparator

C + + overloaded comparison operator = = Java comparator

package com.godzuo.java;

import java.util.Arrays;
import java.util.Comparator;

public class Comparator {

	public static class Student {
		public String name;
		public int id;
		public int age;

		public Student(String name, int id, int age) {
			this.name = name;
			this.id = id;
			this.age = age;
		}
	}

	public static class IdAscendingComparator implements Comparator<Student> {
		//Sort in ascending order by Id

		//!!! below!!!
		//When a negative number is returned, the first parameter comes first
		//When returning a positive number, the second parameter comes first
		//It doesn't matter who is in front when returning 0
		
		@Override
		public int compare(Student o1, Student o2) {
			return o1.id - o2.id;
			
			//if(o1.id < o2.id)
			//	return -1;
			//if(o1.id > o2.id)
			//	return 1;
			//return 0;
		}

	}

	public static class IdDescendingComparator implements Comparator<Student> {
		//ID descending order
		@Override
		public int compare(Student o1, Student o2) {
			return o2.id - o1.id;
		}

	}

	public static class AgeAscendingComparator implements Comparator<Student> {
		//Ascending order of age
		@Override
		public int compare(Student o1, Student o2) {
			return o1.age - o2.age;
		}

	}

	public static class AgeDescendingComparator implements Comparator<Student> {
		//Age descending comparator
		@Override
		public int compare(Student o1, Student o2) {
			return o2.age - o1.age;
		}

	}

	public static void printStudents(Student[] students) {
		for (Student student : students) {
			System.out.println("Name : " + student.name + ", Id : " + student.id + ", Age : " + student.age);
		}
		System.out.println("===========================");
	}

	public static void main(String[] args) {
		Student student1 = new Student("A", 2, 20);
		Student student2 = new Student("B", 3, 21);
		Student student3 = new Student("C", 1, 22);

		Student[] students = new Student[] { student3, student2, student1 };
		printStudents(students);

		Arrays.sort(students, new IdAscendingComparator()); //System comparison size: array, policy
		printStudents(students);

		Arrays.sort(students, new IdDescendingComparator());
		printStudents(students);

		Arrays.sort(students, new AgeAscendingComparator());
		printStudents(students);

		Arrays.sort(students, new AgeDescendingComparator());
		printStudents(students);
        
        //Built in heap structure
		PriorityQueue<Student> heap = new PriorityQueue<>(new AgeAscendingComparator());
		heap.add(student1);
		heap.add(student2);
		heap.add(student3);
		while (!heap.isEmpty()){
			Student student = heap.poll();
			System.out.println("Name : " + student.name + ", Id : " + student.id + ", Age : " + student.age);
		}

	}
}

• Comparators can also be used in ordered structures
  1. If you don't transfer things, it is organized by small root heap by default

public static void main(String[] args){
	PriorityQueue<Integer> heap = new PriorityQueue<>(); 

	heap.add(8);
	heap.add(4);
	heap.add(9);
	heap.add(10);
	heap.add(3);

	while(!heap.isEmpty())
		System.out.println(heap.poll());
}

2. Pass to comparator, sort by large root heap

public class HeapTest{

	public static class AComp implements Comparator<Integer> {

		//!!! below!!!
		//Returns a negative number, with the first parameter listed above
		//Returns a positive number, with the second parameter listed above
		//When you return 0, it doesn't matter who is in front
		@Override
		public int compare(Integer arg0, Integer arg1) {
			return arg1 - arg2;
		}

	}
	
	public static void main(String[] args){
		PriorityQueue<Integer> heap = new PriorityQueue<>(new AComp()); //Incoming comparator

		heap.add(8);
		heap.add(4);
		heap.add(9);
		heap.add(10);
		heap.add(3);

		while(!heap.isEmpty())
			System.out.println(heap.poll());
	}
}

• The essence of comparator is to overload comparison operators
• The comparator can be well applied to the sorting of special standards
• The comparator can be well applied to the structure sorted according to special standards (such as heap)

6, Cardinality sort

Sorting not based on comparison is based on data conditions, and has less application scope than sorting based on comparison. (eg: count sort, cardinality sort)

Put them into the bucket in order according to the number, ten, hundred, thousand, ten thousand, etc., and then pour them out in order.
The highest priority is the last.

Base sorting: there should be base (base digits = = number of buckets)

import java.util.Arrays;

public class RadixSort{

	//only for no-negative value
	public static void radixSort(int[] arr){
		if(arr == null || arr.length < 2){
			return;
		}
		radixSort(arr,0,arr.length - 1,maxbits(arr));
	}
	
	public static int maxbits(int[] arr){
		int max = Integer.MIN_VALUE;
		for(int i = 0;i < arr.length;i++){
			max = Math.max(max,arr[i]);   //Maximum found
		}
		int res = 0;
		while(max != 0){
			res++;
			max /= 10;
		}
		return res;   //How many decimal digits does the maximum have
	}
	
	//arr[begin...end] sort
	public static void radixSort(int[] arr,int L,int R,int digit){
	//The number of decimal digit s in this batch is R to L
		final int radix = 10;   //Based on 10 bits
		int i = 0,j = 0;
		//How many auxiliary spaces are there
		int[] bucket = new int[R - L + 1];
		for(int d = 1;d <= digit;d++){  //The number of bits in and out of the bucket is the number of times, that is, the traversal of the number of bits
			//10 spaces
			//count word frequency array = > prefix and
			//count[0] is the number of numbers whose current bit (d bit) is 0
			//count[1] is the number of current bits (d bits) that are (0 and 1)
			//count[2] is the number of numbers whose current bits (d bits) are (0, 1 and 2)
			//count[0] is the number of current bits (d bits) that are (0~i)
			int[] count = new int[radix];    //count[0...9]
			for(i = L;i <= R;i++){
				j = getDigit(arr[i],d); //d=1 takes out one digit number, d=2 takes out one hundred digit number
				count[j]++;  //Calculate the number of each number at each location
			}
			for (i = 1;i < radix;i++){
				count[i] = count[i] + count[i - 1];  //Calculate prefix and
			}
			for(i = R;i >= L;i--){    //Array traversal from right to left
				j = getDigit(arr[i],d);  //Take out the number of d bits
				bucket[count[j] - 1] = arr[i];  //Put it in the last bit of the slice where the auxiliary array is located
				count[j]--;  //Prefix of j and - 1
			}                                   //Count all the buckets and put them into the bucket
			for(i = L,j = 0;i <= R;i++,j++){
				arr[i] = bucket[j];             //Import the numbers in the bucket into the arr
			}                                   
		}         //Cycle, and the number at the next position will come out of the barrel and into the barrel
	}
	public static int getDigit(int x,int d){
		return ((x / ((int) Math.pow(10,d - 1))) % 10);
	}
}

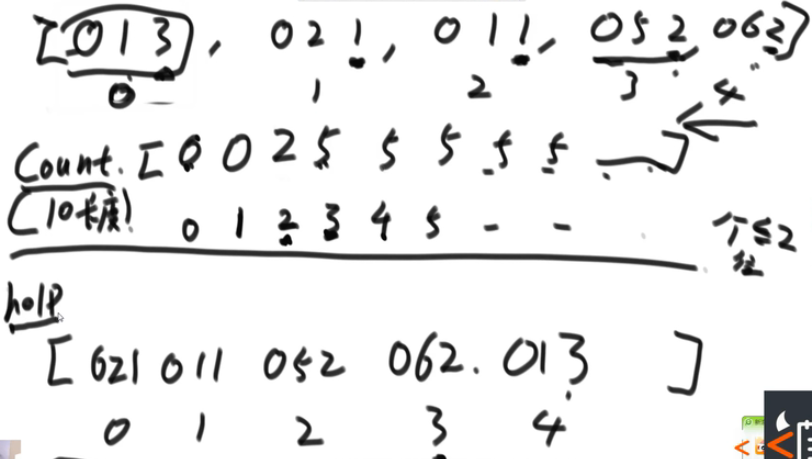
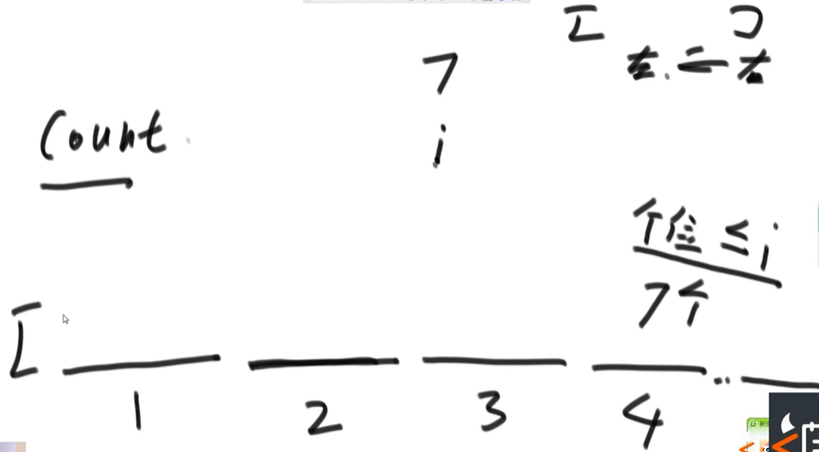
All numbers are traversed from right to left and put into the last position of the piece, which can ensure the first in and first out of the barrel; And from the right, you can count the number less than this number to determine your position.