What is a heap

Maybe the concept is not well understood. Let's look at two pictures below.

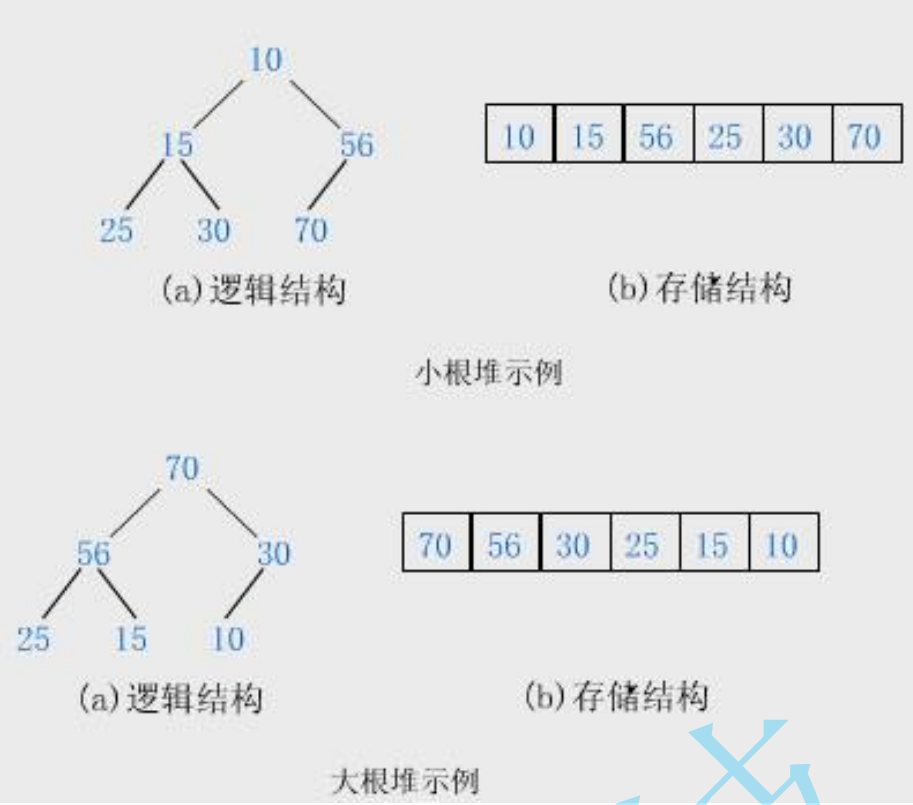
So here comes the question...? The set of data we give can't be so coincidental. It happens to be orderly. At this time, we will introduce an algorithm: the downward sorting algorithm of the heap. Make a group of numbers that are not so regular into a heap.

Heap sort down algorithm

int array[] = {27,15,19,18,28,34,65,49,25,37};

What characteristics can you find from this set of data? It is not difficult to find that except for the root node, the left and right subtrees of this group of data are small heaps. This is also the premise of using the downward adjustment algorithm:
The left and right subtrees must be a heap before they can be adjusted.
Let's look at the adjustment process: let the root exchange with the younger child among its children, then change the child's position to the parent node, and the parent node finds the child node, so as to achieve the purpose of iteration.

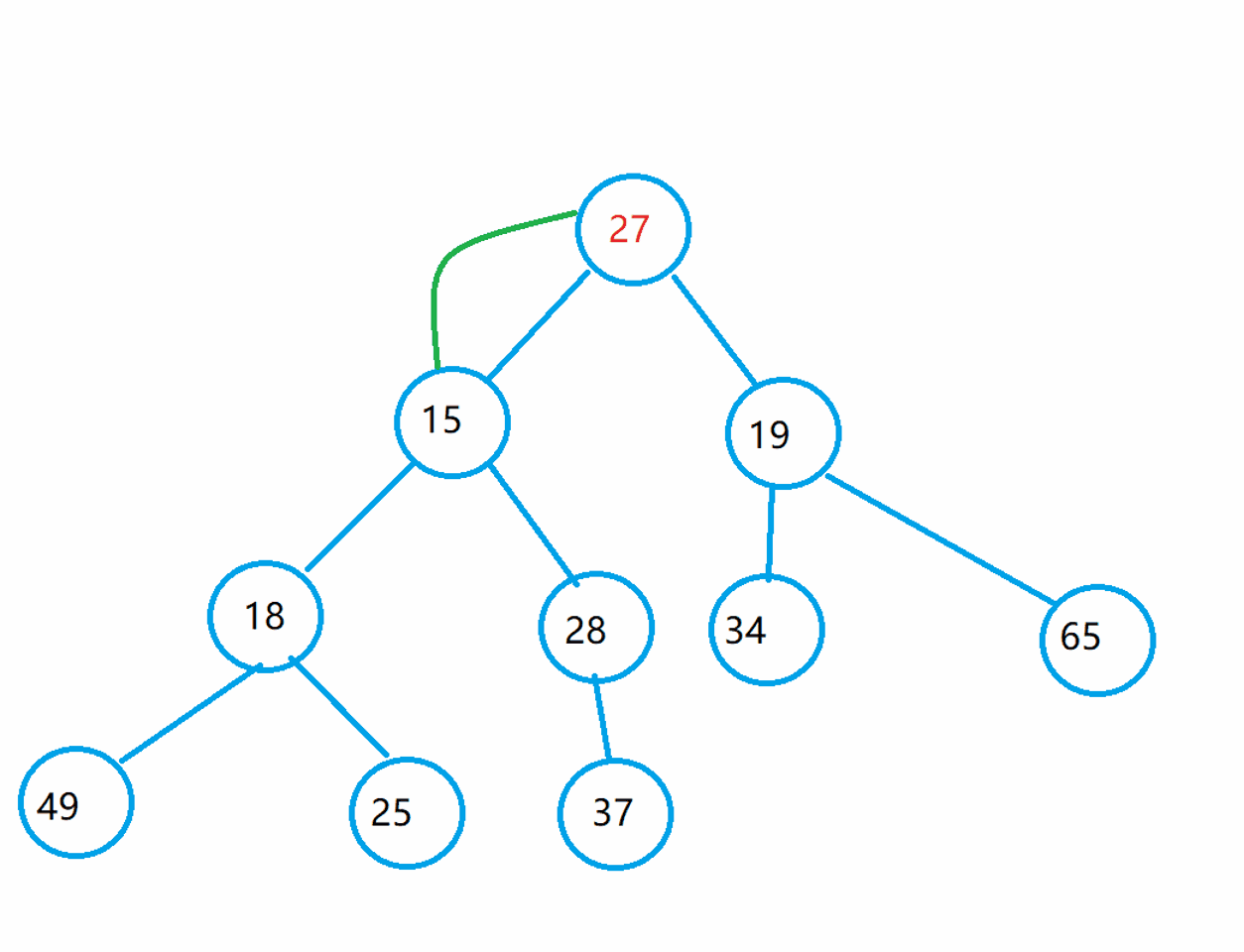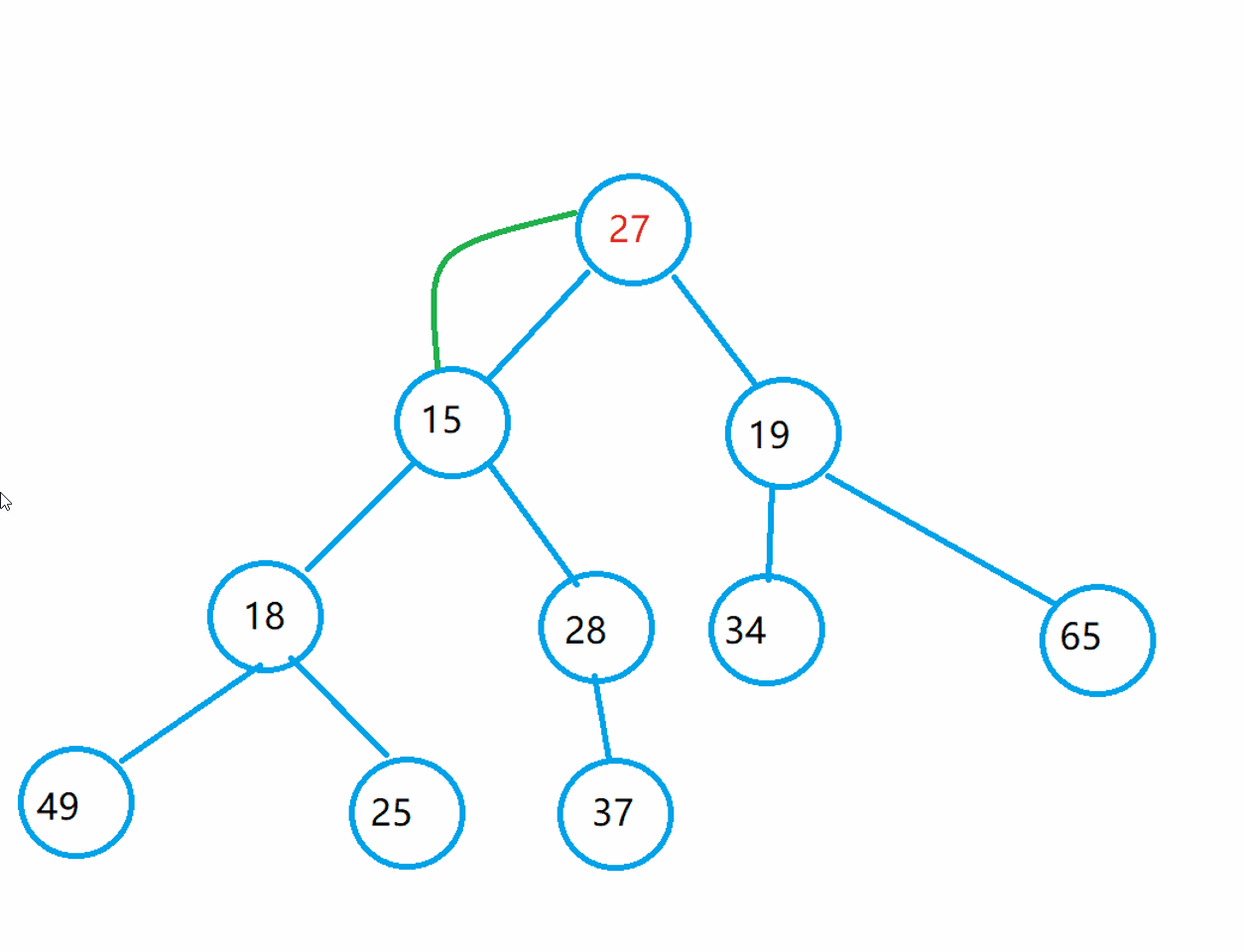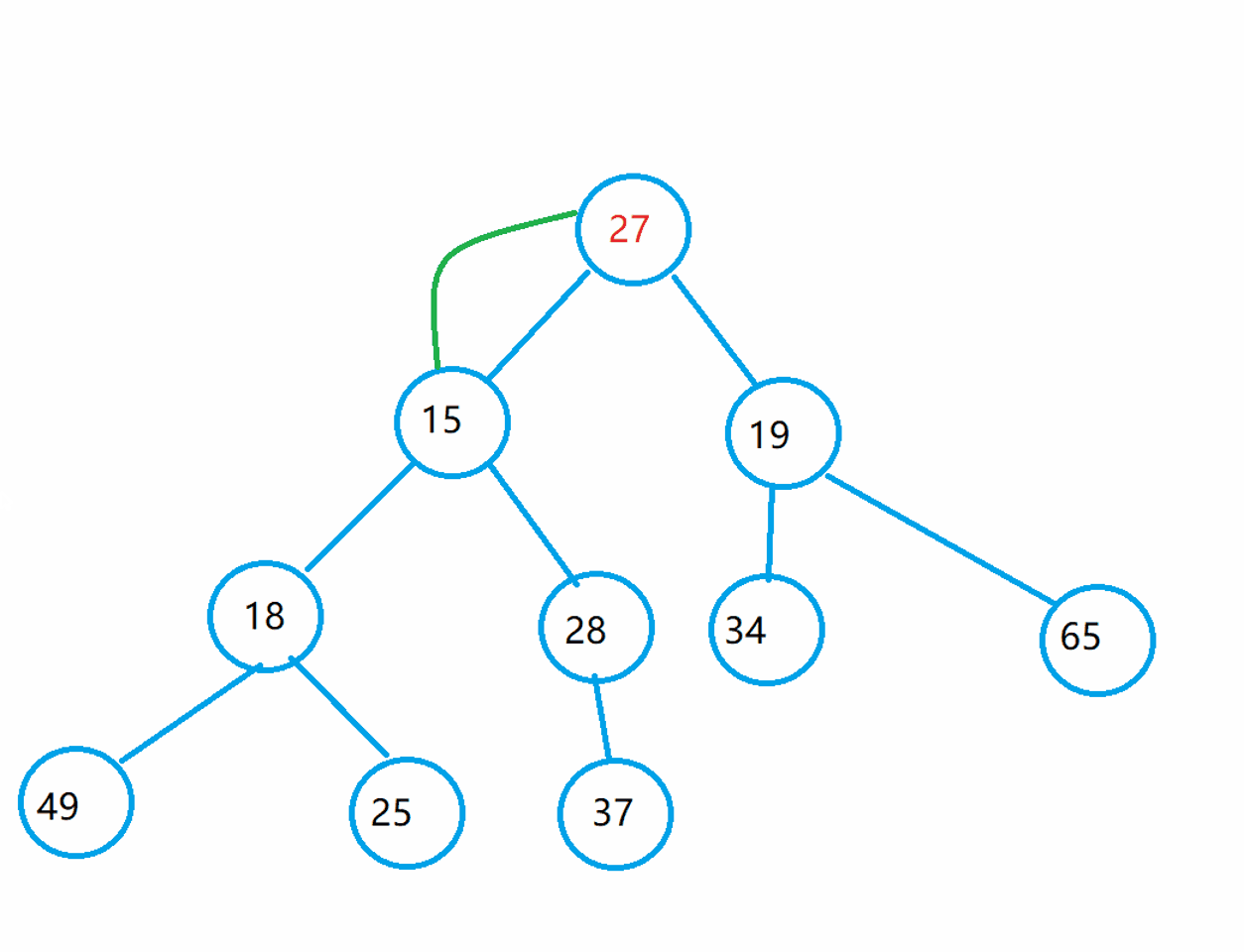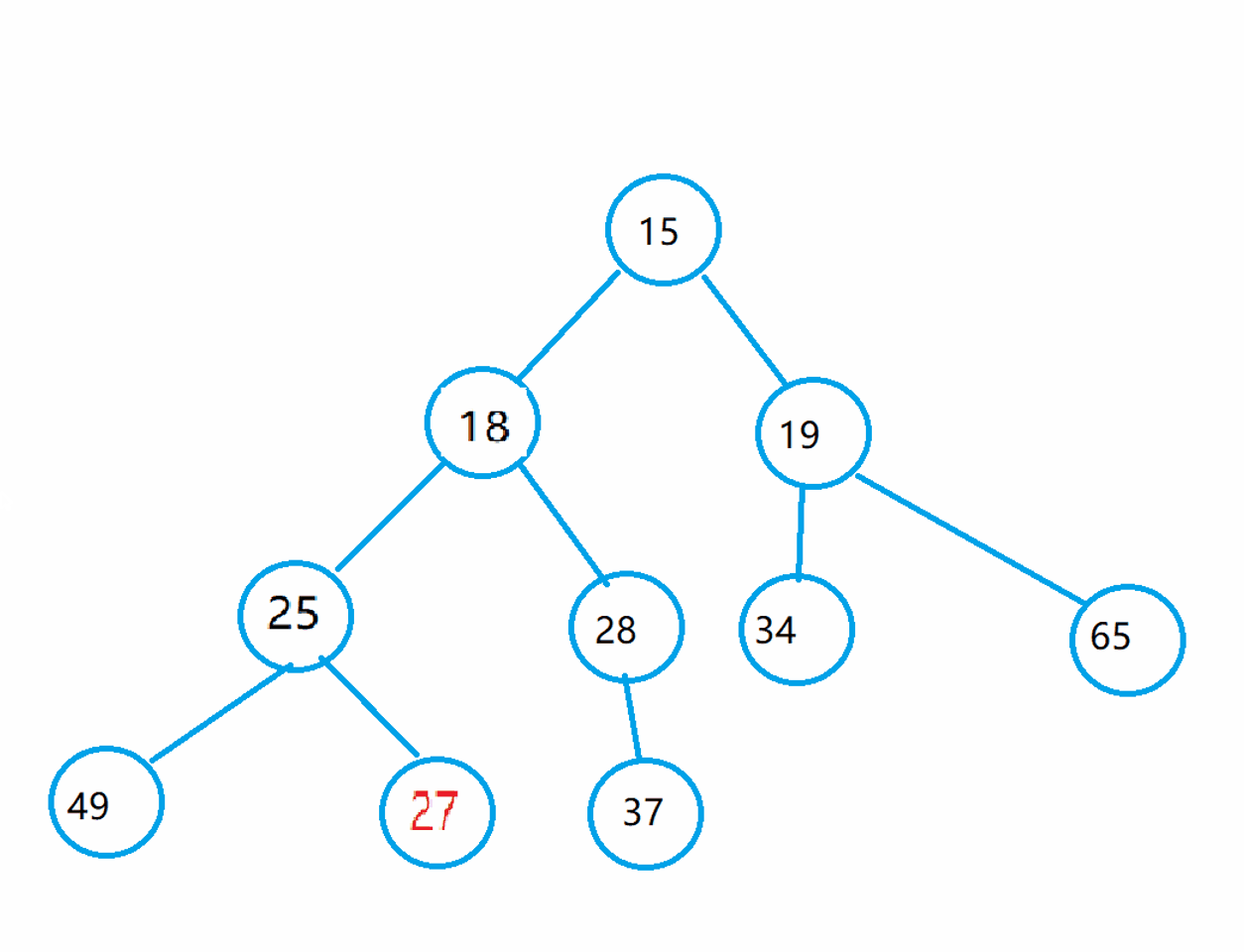
code implementation

void swap(int* children, int* gen)
{
	int temp = *children;
	*children = *gen;
	*gen = temp;
}

//Built a small pile
void Heapdown(int *a, int n,int gen)
{
	//Hypothesis method: assume that the target value is the value you want
	int children = gen * 2 + 1;
	while (children<n)
	{
		if (children+1<n&&a[children + 1] < a[children])
		{
			children++;
		}
		if (a[children] <= a[gen])
		{
			//Send the address, or it won't affect the outside
			swap(&a[children],&a[gen]);
		}
		else
		{
			break;
		}
		gen = children;
		children = gen * 2 + 1;
	}
}

Note:
1. Skillfully use the hypothesis method and assume that the target value is a small child, which can greatly simplify the code.
2. Ensure that children + 1 < n to prevent the array from crossing the boundary.
3. When sending parameters to swap, you should send the address, so as to affect the outside.

How to sort an irregular array down the heap

Here, I'm sure you'll ask if you're smart? What if the given set of data has no rules to follow?
Let's take a look at the beauty of the downward sorting of the heap: from the back to the front to solve this problem.

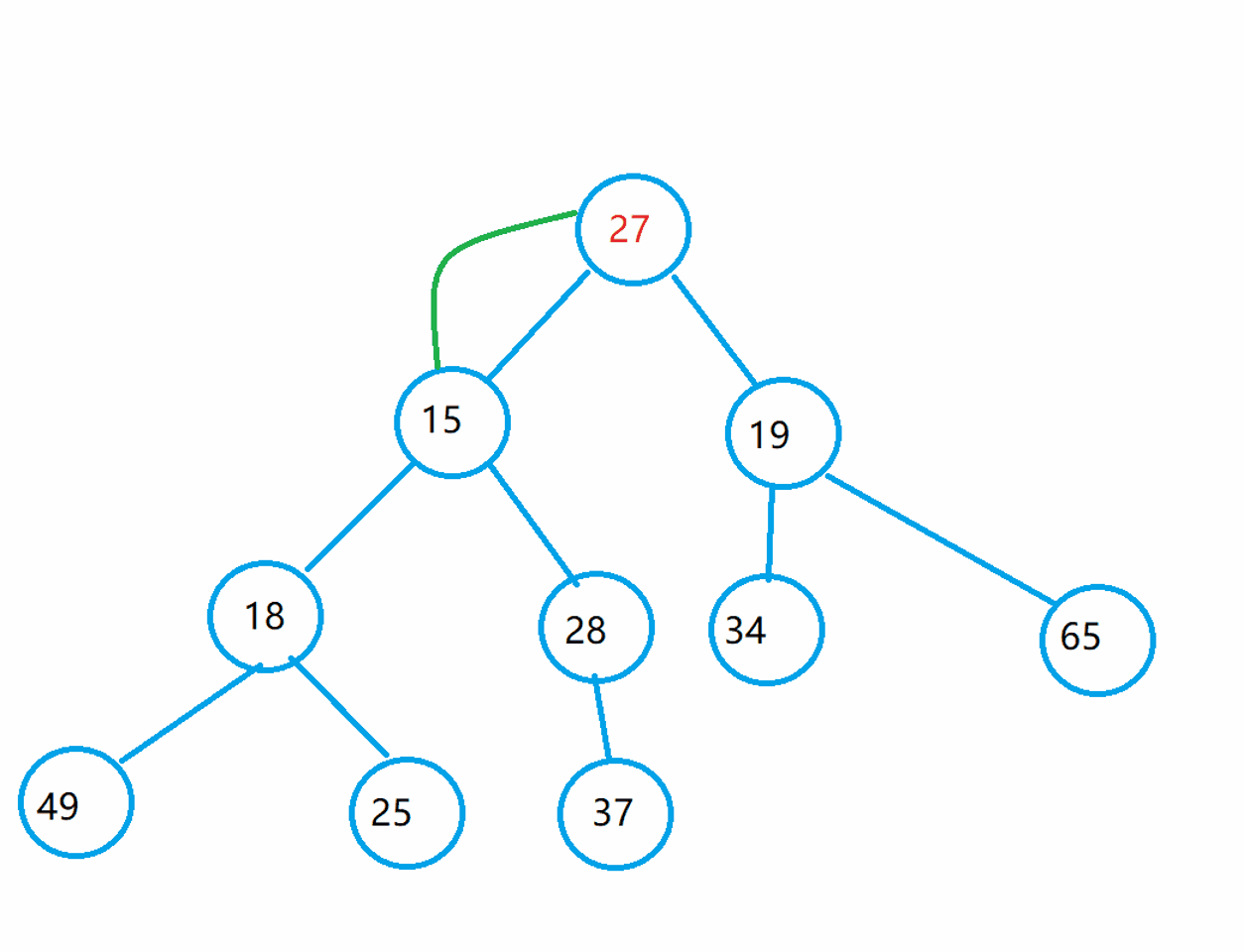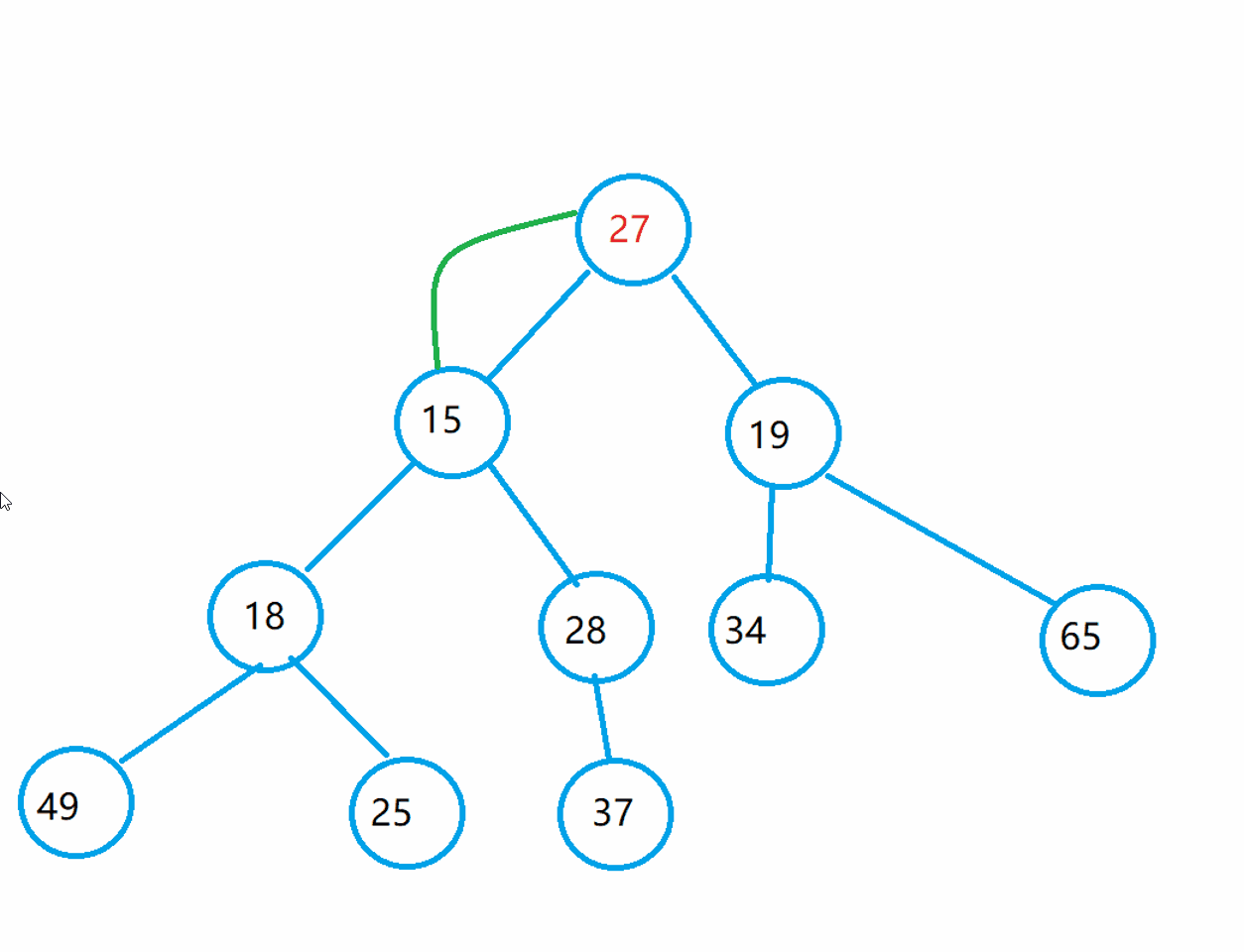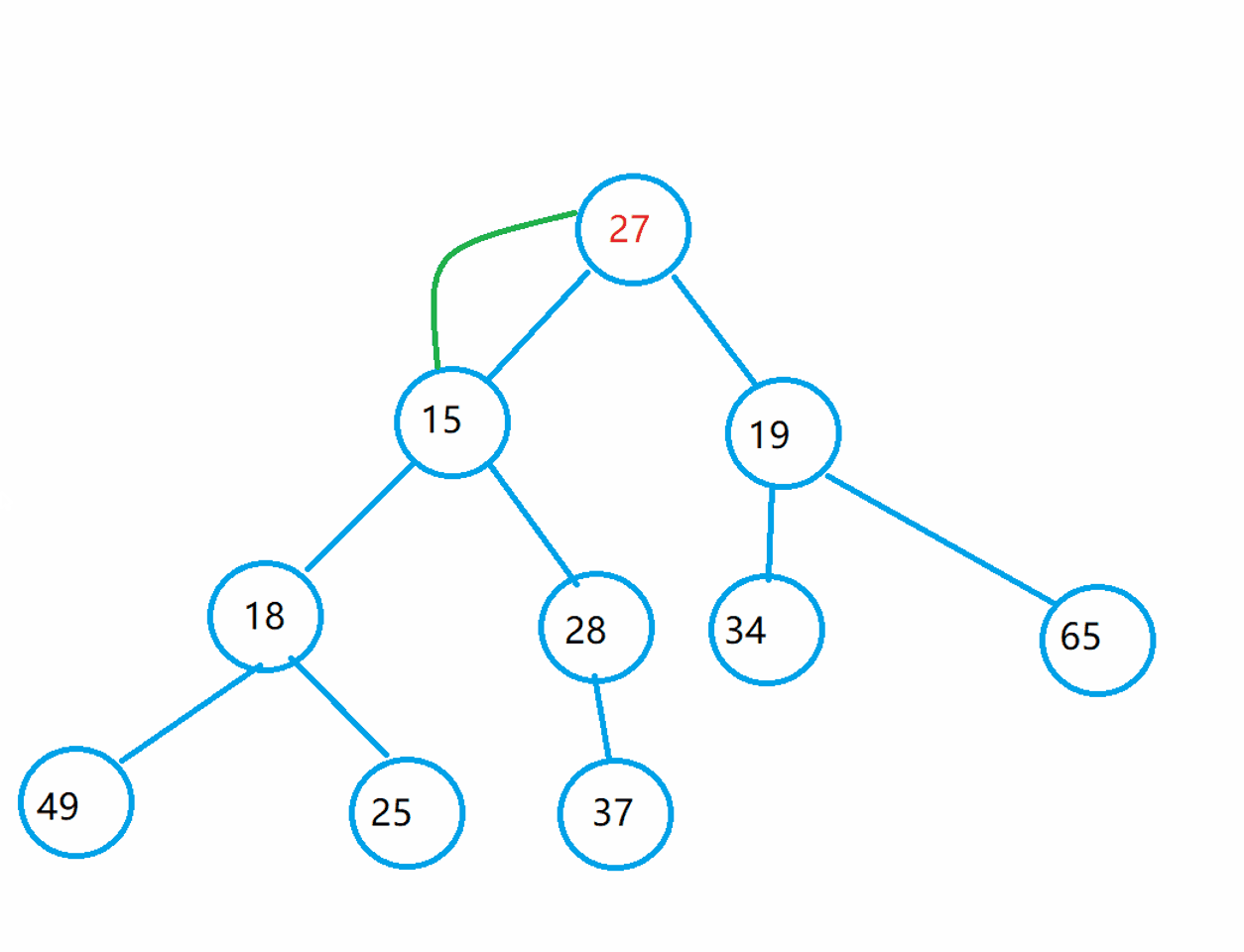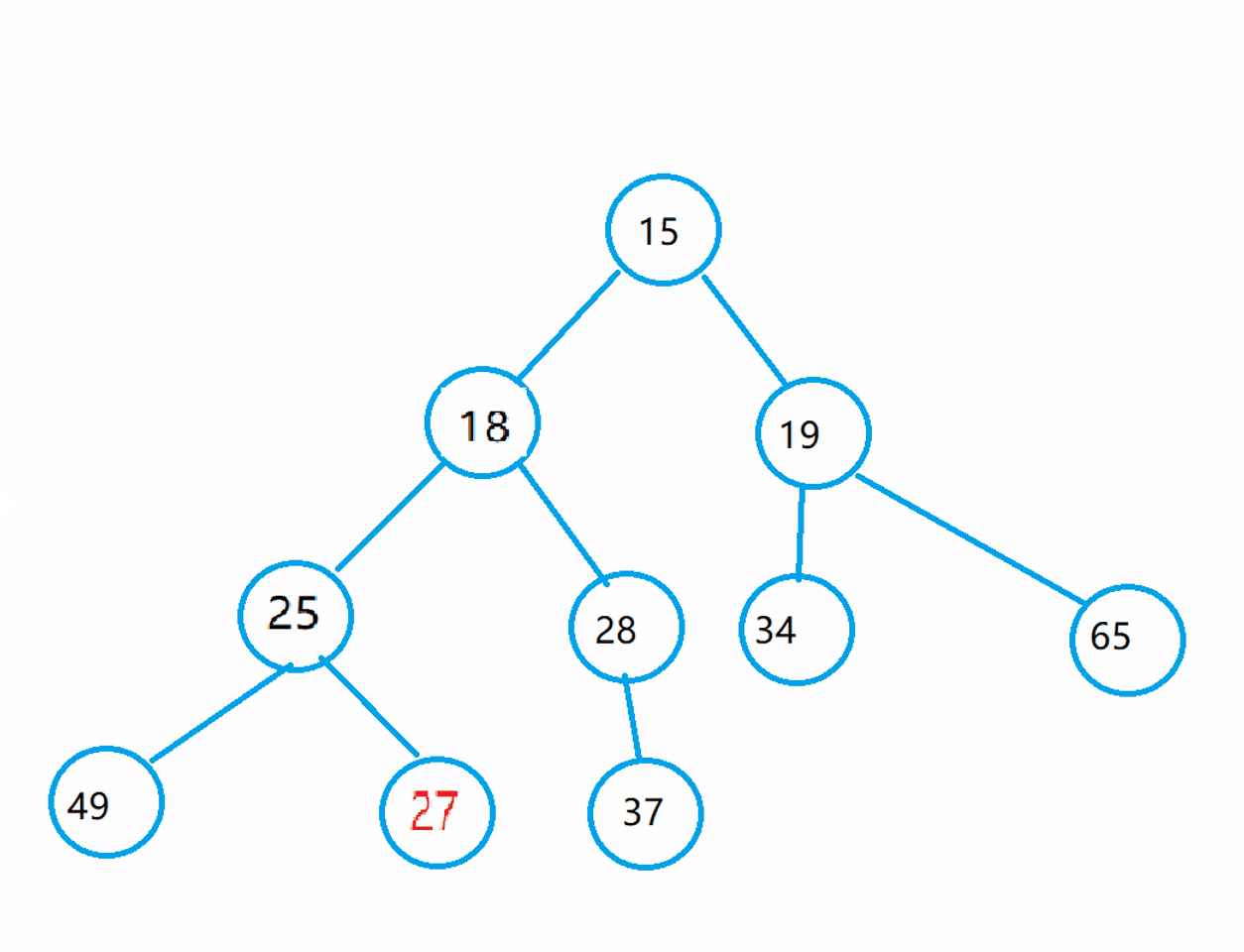
In fact, I understand this idea in this way: if you want the whole tree to become a small pile, you should make each part of it into a small pile and gradually adjust it from the first parent node.

code implementation

void swap(int* children, int* gen)
{
	int temp = *children;
	*children = *gen;
	*gen = temp;
}

//Built a small pile
void Heapdown(int *a, int n,int gen)
{
	//Hypothesis method: assume that the target value is the value you want
	int children = gen * 2 + 1;
	while (children<n)
	{
		if (children+1<n&&a[children + 1] < a[children])
		{
			children++;
		}
		if (a[children] <= a[gen])
		{
			//Send the address, or it won't affect the outside
			swap(&a[children],&a[gen]);
		}
		else
		{
			break;
		}
		gen = children;
		children = gen * 2 + 1;
	}
}


int main()
{
	int a[] = { 27, 15, 18, 13, 19, 21, 28, 29, 1, 2 };
	int sz = sizeof(a) / sizeof(int);
	int gen = (sz - 1 - 1) / 2;
	int i = gen;
	for (i = gen; i >= 0; i--)
	{
		//Adjust the algorithm downward to build the heap
		Heapdown(a, sz, i);
	}
	for (i = 0; i < sz; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

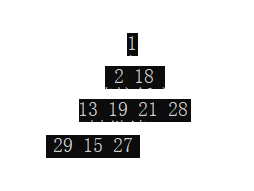
Note: note the relationship between the parent node and the child node.

Time complexity of reactor building

To this person, you might ask? So what is the time complexity of building the reactor?
Let's take a look at the derivation process (the words may be ugly, please forgive me):

Heap sort

In fact, all the things mentioned above are to pave the way for heap sorting.
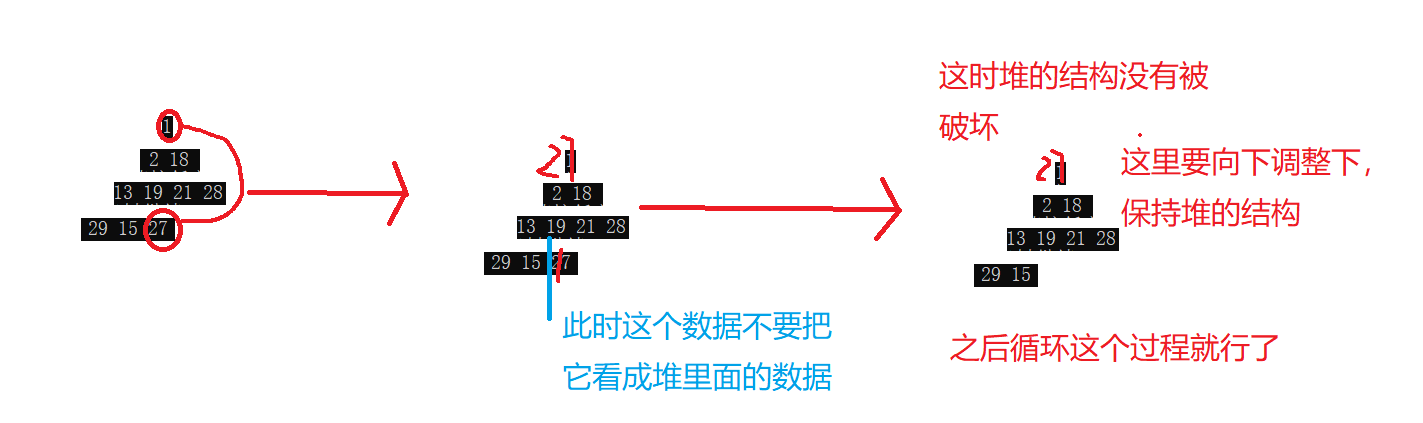
Let's think about a question: if we arrange a group of data in descending order, should we use a small heap or a large heap? I believe many people will answer first: a lot. Because the number of digit 0 is the largest number, and then find the large number again. But in this case, there will be a very serious problem: the structure of the heap is damaged.
Let's take an example:

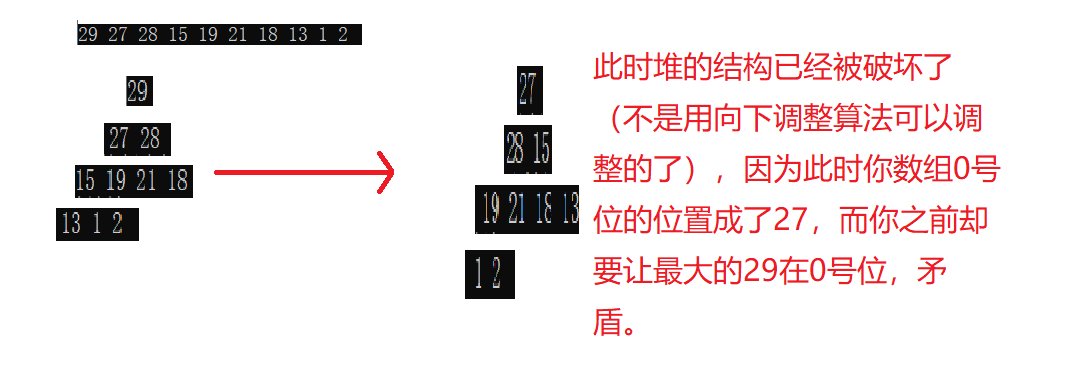
When we look for the largest data again, we find that the structure of the heap has been damaged. If you want to continue looking, you have to build the heap, which is inefficient.
The correct approach should be to build a small reactor:

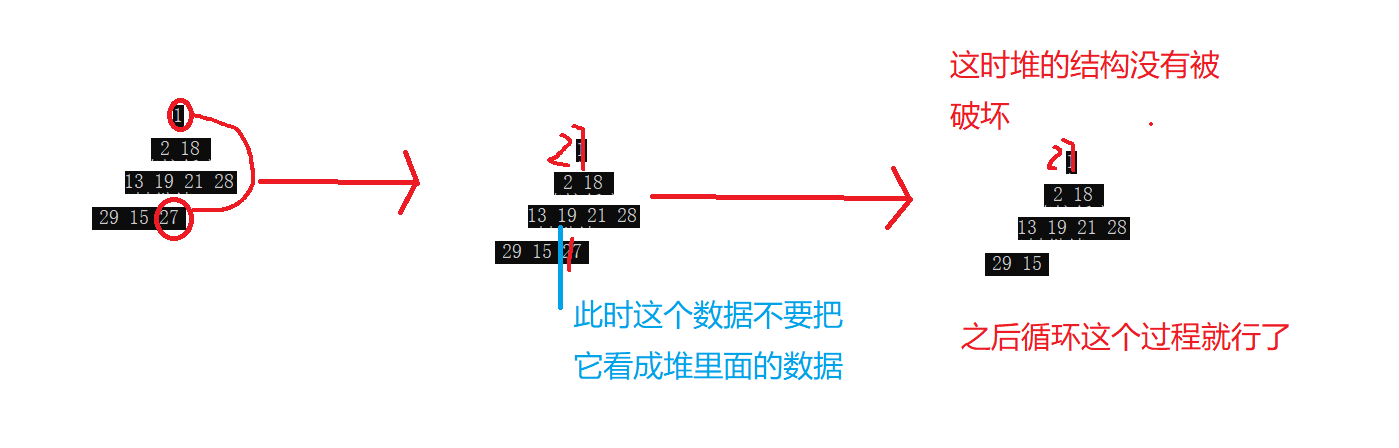
code implementation

void swap(int* children, int* gen)
{
	int temp = *children;
	*children = *gen;
	*gen = temp;
}

//Built a small pile
void Heapdown(int *a, int n,int gen)
{
	//Hypothesis method: assume that the target value is the value you want
	int children = gen * 2 + 1;
	while (children<n)
	{
		if (children+1<n&&a[children + 1] < a[children])
		{
			children++;
		}
		if (a[children] <= a[gen])
		{
			//Send the address, or it won't affect the outside
			swap(&a[children],&a[gen]);
		}
		else
		{
			break;
		}
		gen = children;
		children = gen * 2 + 1;
	}
}

int main()
{
	int a[] = { 27, 15, 18, 13, 19, 21, 28, 29, 1, 2 };
	int sz = sizeof(a) / sizeof(int);
	int gen = (sz - 1 - 1) / 2;
	int i = gen;
	for (i = gen; i >= 0; i--)
	{
		//Adjust the algorithm downward to build the heap
		Heapdown(a, sz, i);
	}
	//Heap sorting, if you use a small heap, it is in descending order
	//With a lot of words, it is in ascending order
	int end = sz - 1;
	for (end = sz - 1; end > 0;)
	{
		swap(&a[0],&a[end]);
		end--;
		sz--;
		for (i = (sz - 1 - 1) / 2; i >= 0; i--)
		{
			Heapdown(a, sz, i);
		}
	}
	sz = sizeof(a) / sizeof(int);
	for (i = 0; i < sz; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

Note:
1. Pay attention to sz and end size adjustment here.
2. Here we should pay attention to the application of this thought, which is very important in later learning.