There are many binary search questions in leecode. Generally speaking, when a topic has the following characteristics, you should immediately associate it with the possibility of using binary search:
- The array to be searched is ordered or partially ordered
- The time complexity is required to be lower than O(n), or the time complexity is directly required to be O(log n)
The idea of binary search is well understood, but the boundary conditions are very cumbersome. Many times, the code written can not deal with the boundary conditions well. For example:

At the same time, there are many variants of binary search, such as:

For the summary of these conditions and boundaries, the following article is strongly recommended. It can be said that the mountain is high and the moon is small, and the water comes out.
https://leetcode-cn.com/problems/binary-search/solution/er-fen-cha-zhao-xiang-jie-by-labuladong/
Let's look at specific topics.
The first is a most primitive and typical binary search question:
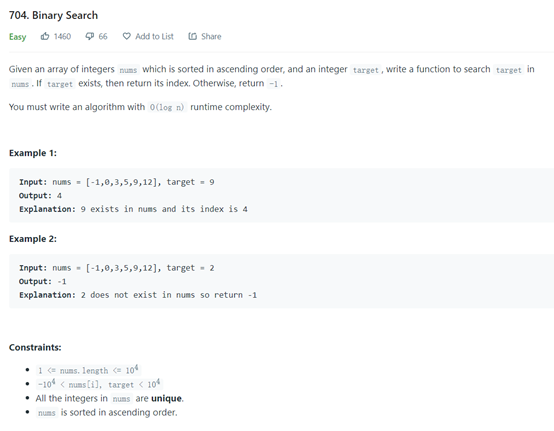
https://leetcode.com/problems/binary-search/
This problem is very typical. We solve it in two ways. The first is
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// The value of right is within the array range, which is [left, right], closed left and closed right,
// It is decided to use left < = right in the while loop
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) return mid;
else if (nums[mid] < target) {
// It is divided into three parts, [left, mid - 1], mid, [mid + 1, right], so left and right take mid + 1 and mid - 1 respectively
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
The second method is [left, right], and the implementation code is as follows:
public int search(int[] nums, int target) {
int left = 0, right = nums.length;
// The value of right is within the range of the array, which is [left, right], closed on the left and open on the right,
// It is decided to use left < right in the while loop
int mid = -1;
while(left < right) {
mid = left + (right - left) / 2;
if (nums[mid] == target) return mid;
// It is divided into three parts, [left, mid), mid, [mid+1, right), so left and right take mid + 1 and mid respectively
else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid;
}
}
return -1;
}
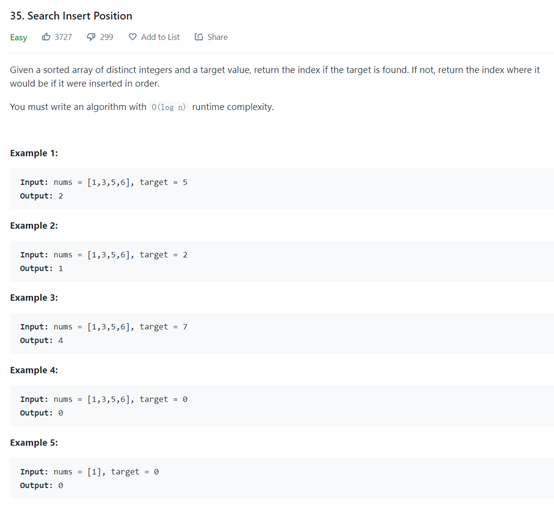
https://leetcode.com/problems/search-insert-position/
This topic is to find the location of the insert. Compared with whether the result of the previous topic is found, you only need to return left when it cannot be found. The current exit condition is left == right, so you can return any one.
public int searchInsert(int[] nums, int target) {
int left = 0, right = nums.length;
while(left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) return mid;
else if (nums[mid] > target) {
right = mid;
} else {
left = mid + 1;
}
}
// The exit condition is left == right, so you can return any one
return left;
}
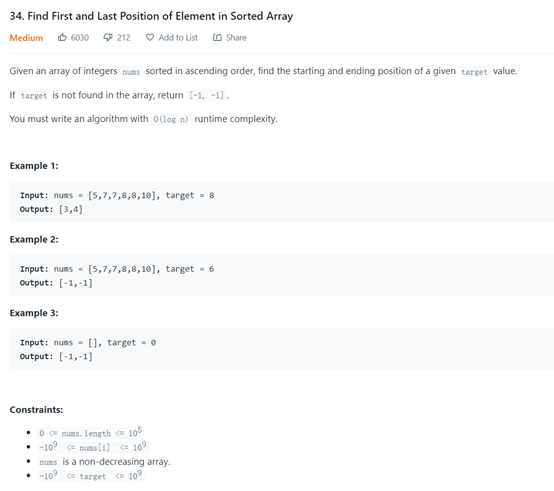
https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/
This problem needs to find the location of the first occurrence and the location of the last occurrence, that is, find twice, one time to find the left boundary through the left approximation, the other time to find the right boundary through the right approximation, and then return the result.
The implementation code still adopts two loop methods, which are implemented respectively.
The method of < = is adopted:
public int[] searchRange(int[] nums, int target) {
int len = nums.length;
if (len == 0) return new int[]{-1, -1};
int[] res = new int[]{-1, -1};
res[0] = left_bound(nums, target);
res[1] = right_bound(nums, target);
return res;
}
// Use [left, right] to implement
private int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1; // [left, right] - > determines the use of left < = right in the while loop
// Left approximation
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) { // The essence is to find the left position, which represents the left side of the left, which is a set smaller than the target
left = mid + 1;
} else if (nums[mid] >= target) { // For the left approximation, when it is equal, take right = mid, so continue to find the first place where the value appears
right = mid - 1;
}
}
// Note that when it is not found, left may be equal to nums Length, Num [left] will also overflow, so this situation is excluded
if (left < nums.length && nums[left] == target) return left;
else return -1;
}
// Use [left, right] to implement
private int right_bound(int[] nums, int target) {
// Right approximation
int left = 0, right = nums.length - 1; // [left, right] - > determines the use of left < = right in the while loop
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] > target) { // It can be understood that the positions on the right side of right are collections larger than target
right = mid - 1;
} else if (nums[mid] <= target) { // For the right approximation, when it is equal, take left = mid + 1, so continue to find the last place where the value appears
left = mid + 1;
}
}
// Note that if this place is not found, the left may be 0, so - 1 will overflow
if (right >= 0 && nums[right] == target) return right;
else return -1;
}
The method of < is adopted, which is different from the assignment of left and right.
public int[] searchRange(int[] nums, int target) {
int len = nums.length;
if (len == 0) return new int[]{-1, -1};
int[] res = new int[]{-1, -1};
res[0] = left_search(nums, target);
res[1] = right_search(nums, target);
return res;
}
private int left_search(int[] nums, int target) {
int left = 0, right = nums.length;
// Left approximation
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] >= target) {
right = mid;
}
}
if (left < nums.length && nums[left] == target) return left;
else return -1;
}
private int right_search(int[] nums, int target) {
// Right approximation
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > target) {
right = mid;
} else if (nums[mid] <= target) {
left = mid + 1;
}
}
if (left >= 1 && nums[left - 1] == target) return left - 1;
else return -1;
}
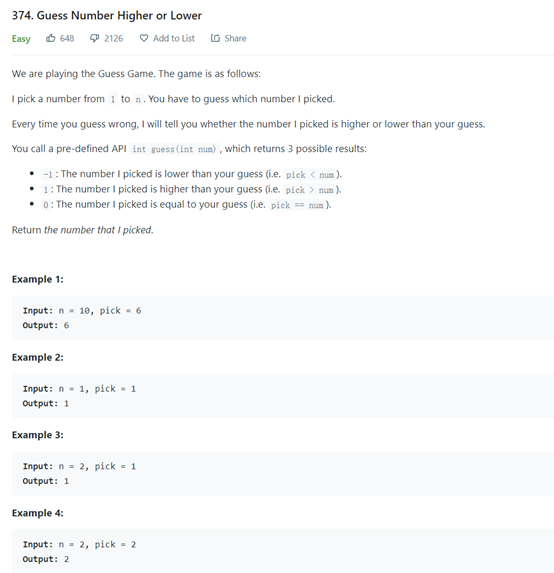
https://leetcode.com/problems/guess-number-higher-or-lower/
There's nothing to say about this feeling It is most important to understand the subject
public int guessNumber(int n) {
int left = 1, right = n;
int mid = 0;
while(left <= right) {
mid = left + (right - left) / 2;
if (0 == guess(mid)) break;
else if (1 == guess(mid)) left = mid + 1;
else right = mid - 1;
}
return mid;
}
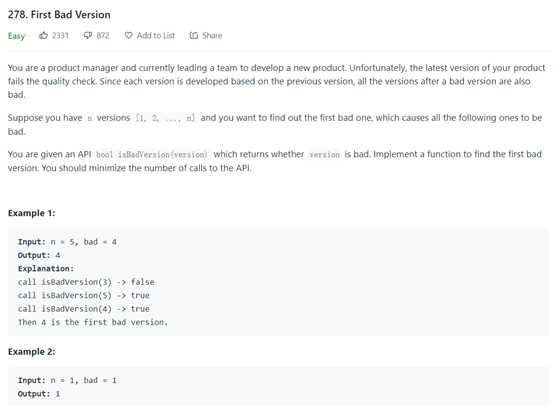
https://leetcode.com/problems/first-bad-version/
This question is equivalent to finding the true that appears for the first time. It is also implemented in the way of the left after all. The code is as follows:
public int firstBadVersion(int n) {
int left = 1, right = n;
int mid = -1;
while(left < right) {
mid = left + (right - left) / 2;
if (isBadVersion(mid)) right = mid; // If true is found, right = mid
else left = mid + 1; // If false is found, left is marked as mid + 1
}
return left;
}
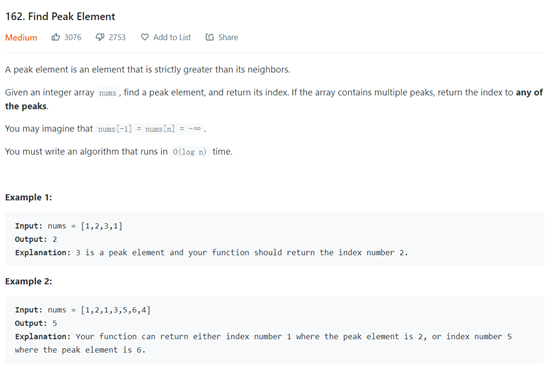
https://leetcode.com/problems/find-peak-element/
To find the extreme value of the peak, you can also use binary search. Note that the maximum right at this time can only be length – 1 (* * * special attention) because the peak height at mid and mid + 1 should be compared.
public int findPeakElement(int[] nums) {
if (nums.length == 1) return 0;
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < nums[mid + 1]) { // On the rising curve, one of the peak extreme values is on the right. Note that due to the judgment of mid + 1, the above right = num Length - 1, otherwise it will overflow
left = mid + 1;
} else { // In the descending curve, one of the extreme values of the peak is on the left
right = mid;
}
}
return left;
}