Title Description & Links

Leetcode 907 : given an array, find the minimum values of all subarrays and return the sum of all minimum values

Topic idea

1. Enumeration of violence

The intuitive idea is to enumerate all subarrays through violence and find the sum of the minimum values of all subarrays, because the topic subarray refers to continuous subarrays, and all violent enumeration is the starting point and ending point of violence, with two layers of for loop. Then, in the process of traversal, the challenge arena saves the current minimum value and sums it. Direct code:

 public int sumSubarrayMins(int[] arr) {
        // Violence solution starting point and ending point
        int res = 0;
        
        // List all ranges
        for(int st=0; st<arr.length; st++) {
            int min = arr[st];
            
            
            for(int ed=st; ed<arr.length; ed++) {
                if(arr[ed]<min) min = arr[ed];
                res = (res+min)%100_000_0007;
            }
        }
        
        return res;
        
    }

Violence enumeration needs to enumerate all start and end points. Time complexity: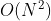； Space complexity:.  

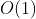2. Reverse thinking + monotonous stack

The idea of this problem is the same as Leetcode 828 Similarly, our forward thinking will find ways to find all subarrays and then find their minimum value. Can we change our thinking and find a value to solve the range in which this value can act as the minimum value.

For example: there is an array [3,1,2,4], I look for each point as the range of the minimum value

Array : [3, 1, 2, 4]

The current value is 3, the previous one on the left<3 Location of-1(No,)，Next on the right<3 Location 1
- The starting point belongs to(-1, 0]，The termination point belongs to[0, 1),Only subarray is[3]The minimum value is 3 when => (0-(-1))*(1-0) = 1 Kinds of situations

The current value is 1, the previous one on the left<1 Location of-1(No,)，Next on the right<1 Location 4(No,)
- The starting point belongs to(-1, 1]Select any one, and the termination point belongs to[1, 4)Choose one,The minimum value of subarray is 1 => (1-(-1))*(4-1) = 6 Kinds of situations

The current value is 2, the previous one on the left<2 Position 1, next on the right<2 Location 4(No,)
- The starting point belongs to(1, 2]Only 2 can be selected, and the end point belongs to[2, 4)Choose one,The minimum value of subarray is 2 => (2-1)*(4-2) = 2 Kinds of situations


The current value is 4, the previous one on the left<4 Position 2, next on the right<4 Location 4(No,)
- The starting point belongs to(2, 3]，The termination point belongs to[3, 4),The minimum value of subarray is 4 => (3-2)*(4-3) = 1 Kinds of situations

Total number of subarrays: 1+6+2+1 = 10 Kinds of situations
- Verify the number of subarrays with an array length of 4:
    Subarray length=1(4 species) + 
    Subarray length=2([3,1],[1,2],[2,4]3 Kinds of situations) + 
    Subarray length=3(two types) + 
    Subarray length=4(1 species) 
    = 10 species

As long as we know the position of the previous < X and the latter < X of each element X, we can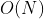Complete the summation in time. So how to solve the position of the former element smaller than him and the latter element smaller than him? This is the problem solved by monotone stack.

• Monotone stack: refers to that the elements stored in a stack meet the monotonic increasing or decreasing relationship
• Monotone stack - concept template Title: Leetcode 496. Next Greater Element
• The most typical application of monotone stack is to solve these two kinds of questions:
  • Find the previous position of the current element that is greater than or less than its value
  • Find the next position of the current element that is greater than or less than its value

Through the monotone stack, if you record a position less than the current value, the specific idea is to maintain a monotone increasing stack: traverse the array. If the next element is larger than the element in the current stack, then add it to the stack. If it is smaller than the top of the stack, pop out all the elements in the stack that are greater than the value. This value is the next position of these elements that are less than these elements, The code is as follows:

int n = arr.length;

int[] nextSmall = new int[n];
Arrays.fill(nextSmall, n); // If there is no next smaller value, the default value is arr.length
Stack<Integer> stk = new Stack<>();
stk.push(0); // Push the first element position onto the stack

for(int i=1; i<arr.length; i++) {
    while(!stk.isEmpty() && arr[i]<arr[stk.peek()]) {
        // If an element smaller than the top of the stack appears, stack pop
        int idx = stk.pop();
        nextSmall[idx] = i;
    }
    stk.push(i);
}

Similarly, if the previous position is less than the current value, it can be solved by traversing from back to front.

• When duplicate elements appear in the array

In the previous example, there are no duplicate elements. We need to consider whether to introduce duplicate subarrays if there are duplicate elements. As can be seen from the following example, we should look for the previous position less than or equal to the current value, so as to avoid the problem of duplicate solution caused by introducing a position equal to the current value.

Add array [3, 1, 4, 1, 2]

3 Minimum range (0-(-1))*(1-0) = 1 species

index=1 Use 1 on as the minimum range (1-(-1))*(5-1) = 8 species

4 Make minimum range (2-1)*(3-2) = 1 species

index=3 Use 1 on as the minimum range (3-(-1))*(5-3) = 8 species
- !!!There is a problem here. The starting point includes index=1 1 at leads to repeated solutions, so when selecting the starting point, the point before the previous 1 should not be selected

2 As minimum range (4-3)*(5-4) = 1 species

In this way, the overall idea of this problem is relatively clear, and the code is as follows:

class Solution {
    public int sumSubarrayMins(int[] arr) {
        // Traverse each element and find the position behind it, which is smaller than that of the front element
        int n = arr.length;
        int[] lmin = new int[n];
        Arrays.fill(lmin, -1);
        int[] rmin = new int[n];
        Arrays.fill(rmin, n);
        
        Stack<Integer> stk1 = new Stack<>();
        Stack<Integer> stk2 = new Stack<>();
        stk1.push(0); // add first element
        stk2.push(arr.length-1);
        
        // Before and after smaller elements, monotonically increasing stack
        for(int i=1; i<arr.length; i++) {
            // If increasing and decreasing is to find the next one smaller than him
            while(!stk1.isEmpty() && arr[i]<arr[stk1.peek()]) {
                int idx = stk1.pop();
                rmin[idx] = i;
            }
            stk1.push(i);
        }
        
        for(int i=arr.length-2; i>=0; i--) {
            // If it is added incrementally, if it is small, the previous value smaller than it will be found
            while(!stk2.isEmpty() && arr[i]<=arr[stk2.peek()]) {
                int idx = stk2.pop();
                lmin[idx] = i;
            }
            stk2.push(i);
        }
        
        // Then find the range of each element as the minimum value (i-l)*(r-i)*val
        long res = 0;
        int mod = 1000_000_007;
        
        for(int i=0; i<arr.length; i++) {
            int l = lmin[i];
            int r = rmin[i];
            long sum = (long)(i-l)*(r-i)*arr[i];
            
            res = (res + sum)%mod;
        }
        
        return (int)res;
    }
}

Time complexity: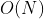； Space complexity: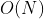, open up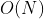To save the monotone stack and the position before and after the current value.