Preface:
There are two main algorithms of hidden Markov prediction model
Approximate algorithm
Viterbi algorithm
Catalog
- Approximate algorithm
- Viterbi algorithm
- CODE implementation
An approximate algorithm
At each time t selects the most likely state at that time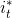
To get a sequence of States
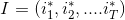, as a prediction result
At time t in state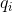
State
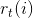Yes,
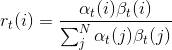
The most probable state at every moment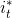For
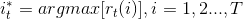
So we can get the state sequence
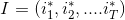
Advantages:
Simple calculation
Disadvantages:
There is no guarantee that the predicted state sequence as a whole is the best possible state sequence,
For example:
The state transition probability of a node is 0, but it is approximate
Viterbi algorithm
In fact, it is to use dynamic programming to solve the hidden Markov model prediction problem (dynamic programming) to find the maximum path strength of probability
Principle: the optimal path has the following characteristics: if the optimal path passes through node a a t time t, then part of the path from node a to terminal t must be optimal for all possible paths.
Proof: if not, then there is a better path from a to T, and if you connect it with the part from i1 to a, there will be a better path.
1. If the path with the highest probability passes through a certain point of the fence network, the sub path from the start point to the point must also have the highest probability from the start to the point.
2. Assuming that there are k states at the i-th moment, there are k shortest paths from the beginning to the i-th moment, and the final shortest path must pass through one of them.
3. According to the above properties, when calculating the shortest path of the i+1 state, only the shortest path from the start to the current k state values and the shortest path from the current state values to the i+1 state values are needed to be considered. For example, the shortest path when t=3 is calculated is equal to the shortest path of all state nodes x2i when t=2 is calculated plus the shortest path of each node from t=2 to t=3.
--------
Copyright notice: This is the original article of CSDN blogger "lake ice 2019", following CC 4.0 BY-SA copyright agreement. Please attach the original source link and this notice for reprint.
Original link: https://blog.csdn.net/hudashi/article/details/87875259
Introduce two variables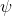
Sum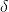
, define all single paths with time t status i
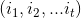The maximum value of medium probability is:
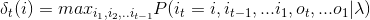
variable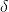The recurrence formula of is
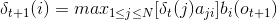
Defined in the t state are all paths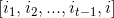
t-1 node of the path with the highest probability
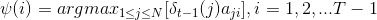
Algorithm flow:
CODE implementation
# -*- coding: utf-8 -*-
"""
Created on Wed Feb 19 09:22:49 2020
@author: chengxf2
"""
import numpy as np
A =[[0.5,0.2,0.3],
[0.3, 0.5,0.2],
[0.2, 0.3, 0.5]]
# Observation matrix 'dry','dryish','damp', 'rainy'
B = [[0.5,0.5],
[0.4, 0.6],
[0.7, 0.3]]
PI = [0.2, 0.4, 0.4]
observations = [0,1,1] ##Red, white, red
class Viterbi:
"""
Args
A: State transition matrix
B: Observation matrix
PI: Initial probability
"""
def __init__(self,A, B, PI,O):
self.A = np.array(A,np.float)
self.B = np.array(B,np.float)
self.PI = np.array(PI,np.float)
self.O = np.array(O,np.int)
self.PSI = None ##Probability maximum
self.DELTA = None ##Path corresponding to probability maximum
def Perdict(self):
T = len(self.O)
BestPath =[]
self.N, self.M = np.shape(self.B)
self.DELTA = np.zeros((T, self.N),np.int)
self.PSI = np.zeros((T, self.N), np.float)
print("\n **********step1 Initialization*****************\n")
obser = self.O[0]
self.PSI[0]=np.multiply(self.PI, self.B[:,obser])
print("\n **********step2 Recurrence*****************\n")
for t in range(1,T):
obser =self.O[t]
for i in range(self.N):
A = np.multiply(self.PSI[t-1] ,self.A[:,i])
index =self.DELTA[t,i]=np.argmax(A)
self.PSI[t,i]=A[index]*self.B[i,obser]
print("PSI ",self.PSI)
DelteI = np.argmax(self.PSI[-1])
BestPath.append(DelteI)
print("\n **********step3 optimal path*****************\n")
for t in reversed(range(T-1)):
index = self.DELTA[t+1,DelteI]
print("\n time:",t,"=>time",t+1, "\t The best node ",index, "=>",DelteI)
DelteI = index
BestPath.append(DelteI)
BestPath.reverse()
print("\n Best path: ",BestPath)
Vier = Viterbi(A,B,PI, observations)
Vier.Perdict()
