Title Description:

Method:

1. Direct calculation method
2. KMP

1. Direct calculation method
Suppose the main string S = "S0S1S2 Sm ", mode string P =" P0P1P2 Pn ".
The implementation method is to compare the string led by Si (0 < = I < = m) and the pattern string p i n the main string s, and determine whether P is the prefix of S. if so, the position where p first appears in S is I, otherwise, then compare the substring starting from Si+1 and the pattern string p; in addition, if I > M-N, the length of the substring led by Si in the main string must be less than the pattern string P I n this case, there i s no need to compare (I > M-N, i.e. M-I < n, i.e. the length of the side substring behind the s string is less than the length of P, obviously P will not be the substring of s at this time).

Code implementation:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time    : 2020/2/4 22:09
# @Author  : buu
# @Software: PyCharm
# @Blog    : https://blog.csdn.net/weixin_44321080
def match(s, p):
    """
    //Determines whether p is a substring of s. if so, returns the first occurrence of p in s
    //Subscript, otherwise return - 1;
    :param s: Main string
    :param p: Pattern string
    :return:
    """
    if s == None or p == None:
        print('Unreasonable parameters!')
        return -1
    slen = len(s)
    plen = len(p)
    if slen < plen:  # p must not be a substring of s
        return -1
    i = 0
    j = 0
    while i < slen and j < plen:
        if list(s)[i] == list(p)[j]:
            # If equal, continue to compare subsequent strings
            i += 1
            j += 1
        else: # s to return the next character of the first character to be compared
            i = i - j + 1 # Originally, i and j are equal, i has been adding 1
            # The above formula cannot be written as i+=1
            j = 0
            if i > slen - plen:#That is, the length of the edge string after s is less than the length of p
                return -1
    if j >= plen: # Matching success
        return i - plen
    return -1


if __name__ == '__main__':
    s = 'xyzabcd'
    p = 'abc'
    print('result:',match(s, p))

Result: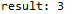

Algorithm performance analysis:
The time complexity is O(m*n);

2.KMP algorithm
In method 1, if "P0P1P2 Pj-1” == “Si-jSi-j+1… Si-1 ", then the first j characters of the mode string have been compared with the characters from i-j to i-1 in the main string. At this time, if PJ! = Si, then the mode string needs to go back to 0, and the main string needs to go back to the position of i-j+1 to start the next comparison again.
In KMP algorithm, if PJ! = Si, there is no need to back off, i.e. I remains still, j does not need to clear, but slides the pattern string to the right, and uses Pk to continue matching with Si. The core of this method is to determine the size of k. obviously, the larger the k, the better.
If PJ! = Si, you can continue to use Pk and Si for comparison, then you must meet the following requirements:
"P0P1P2...Pk-1" ="Si-k...Si-1" (1)
The matched results should meet the following relationship:
"Pj-k...Pj-1" = "Si-k...Si-1" (2)
From (1) (2), it can be concluded that:
"P0P1P2...Pk-1" = "Pj-k...Pj-1"
So when the mode string meets "P0P1P2 Pk-1” = "Pj-k… In Pj-1 ", if the i-th character of the main string fails to match the j-th character of the pattern string, then only the i-th character of the main string needs to be compared with the k-th character of the pattern string.
In order to find the corresponding K value when any character matching fails, the next array is defined here. next[j]=k means: "P0P1P2 Pk-1” = “Pj-k… Pj-1 ", calculated as follows:
(1) next[j] = -1 (when j==0)
(2) Next [J] = max (max {K | 1 < K < J and "P0P1P2 Pk” = “Pj-k-1… Pj-1 "}
(3) next[j] = 0 (other cases)

Code implementation:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time    : 2020/2/5 11:28
# @Author  : buu
# @Software: PyCharm
# @Blog    : https://blog.csdn.net/weixin_44321080
def getNext(p, nexts):
    """
    //Find the next array of strings
    :param p: Character string
    :param nexts: p Of next array
    :return:
    """
    i = 0
    j = -1
    nexts[0] = -1
    while i < len(p):
        if j == -1 or list(p)[i] == list(p)[j]:
            i += 1
            j += 1
            nexts[i] = j
        else:
            j = nexts[j]


def match(s, p, nexts):
    if s == None or p == None:
        print('Unreasonable parameters!')
        return -1
    slen = len(s)
    plen = len(p)
    if slen < plen:
        return -1
    i, j = 0, 0
    while i < slen and j < plen:
        print(f'i={i},j={j}')
        if j == -1 or list(s)[i] == list(p)[j]:
            # If the same, continue to compare the following characters
            i += 1
            j += 1
        else:
            # The main string i does not need to be backtracked. Find the position j of the pattern string to be compared from the next array
            j = nexts[j]
    if j >= plen:
        return i - plen
    return -1


if __name__ == '__main__':
    s = 'abababaabcbab'
    p = 'abaabc'
    lens = len(p)
    nexts = [0] * (lens + 1)
    getNext(p, nexts)
    print('next Array for:', end=' ')
    i = 0
    while i < len(nexts):
        print(nexts[i], end=' ')
        i += 1
    print()
    print('result: ', match(s, p, nexts))

Result: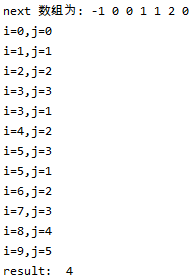

From the operation results, we can see that the next array of pattern string P = "aba abaabc" is [- 1,0,0,1,1], next[3]=1. According to Pk-1=Pj-1, when j=3, k=1, P2=P0. When i=3, j=3, S [i]! = P [J]. At this time, the main string S does not need to be backtracked, and it continues to compare with the character of pattern string position j=next[j]=next[3]=1, because at this time, S[i-1] must be equal to P[0], so there is no need to compare again.

Algorithm performance analysis:
When calculating the next array, the number of cycles is n (n is the length of the pattern string), and when the pattern string matches the main string, the number of cycles is m(m is the length of the main string). So the time complexity of the algorithm is O(m+n).
The spatial complexity is O(n).