I Interview questions and analysis
1. Today's interview question
How do I sort the List collection?
How to sort the List set using Lambda expressions?
2. Topic analysis
The knowledge points investigated in this topic are still related to the List set, but its difficulty has been greatly reduced compared with the previous set content. In fact, this is mainly to investigate our practical application of List set usage and basic features, and to investigate our mastery of sorting when investigating List. On the whole, this topic focuses on our code operation ability, which is not difficult.
Because there are many interview questions in set sorting, this article will be divided into two articles for introduction. Next, let's look at the first article in set sorting!
II List content review
Before sorting the List set, let's review the List set and see if you can remember the set content that brother Yi reviewed with you a few days ago.
1. Introduction
List is an interface with a sequence table, which allows you to store duplicate elements. Common subclasses of this interface are as follows:
- ArrayList: the underlying implementation is based on array. It has fast query, slow addition and deletion, lightweight, but the thread is not safe.
- LinkedList: the bottom layer is based on a two-way linked list. It is fast to add and delete, slow to query, and thread unsafe.
- Vector: the underlying implementation is based on array, which is heavyweight and thread safe, but it is rarely used at present.
2. Common methods
- void add(int index, Object element): adds an object element to the location index;
- boolean addAll(int index, Collection collection): add all elements in the container collection after the index position;
- Object get(int index): get the element with index as the subscript;
- int indexOf(Object element): find the position where the object element first appears in the List;
- int lastIndexOf(Object element): find the last position of the object element in the List;
- Object remove(int index): deletes the element at the index position;
- ListIterator listIterator(int startIndex): returns a ListIterator descendant, starting at startIndex;
- List subList(int fromIndex, int toIndex): returns a sublist list, and the element is stored as an element from fromIndex to toIndex;
- Void sort (comparator <? Super E > C): a method for sorting elements in a collection.
3. Introduction to sorting method of list set
For a List set, if we want to sort it, we mainly sort its internal data elements. Therefore, the sorting problem of List set is mainly transformed into the sorting problem of its internal data elements. As we can see from the introduction of common List methods above, the List collection actually provides us with a sort() sorting method, which we can use to sort data elements.
If the type of the data elements in the List collection is numeric, the sort() method sorts the numbers in ascending order based on the default rules. But if its data type is object type, how should it be sorted? At this time, if we want to sort the collection elements, we need to sort the element objects first. We can customize the sorting of data elements or implement the comparator interface in Java. Therefore, in general, there are four implementation schemes for sorting List sets:
- 1. For simple numeric elements, directly call the sort() method of the collection object or the Collections#sort() method to sort them naturally;
- 2. Custom object sorting: for complex object types, we can customize sorting rules according to the data structure of custom objects;
- 3. Implement Comparator interface sorting in Java: for complex objects, you can also implement two common interfaces in Java, Comparable and Comparator;
- 4. Use Lambda syntax to sort the List set.
Next, Yige will write several cases to demonstrate the code implementation effects of these sorting methods.
III Direct sort for numeric type
1. sort cases
First, we define a List set that stores Integer integers, and sort them directly by the sort() method. The code is as follows:
public static void main(String[] args){
//For numerical data, sort() method is used directly
List<Integer> sortList = new ArrayList<>();
sortList.add(9);
sortList.add(1);
sortList.add(6);
sortList.add(2);
System.out.println("Collection before sorting="+sortList);
sortList.sort(null);
//You can also use the following method to sort in ascending order
//Collections.sort(list);
System.out.println("Sorted collection="+sortList);
}The code execution results are shown in the following figure:
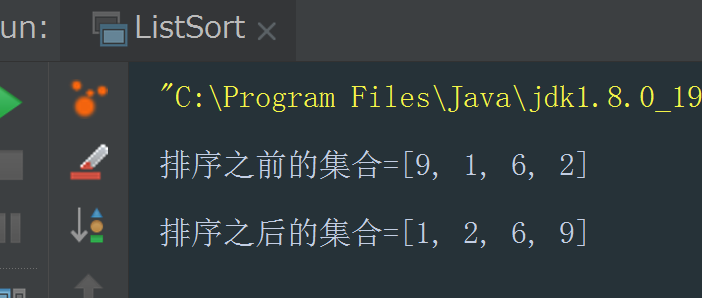
We will find that before the collection sorting, the data elements are disordered; After sorting, the data elements in the collection are automatically arranged in ascending order. If we need to arrange in descending order, we can use the Collections#reverse(list) method.
2. Source code analysis of list #sort() method
At this time, you may wonder why the sort() method in the List can sort the data naturally? Why ascending rather than descending? How is it implemented internally? To figure this out, let's take a look at the source code of the sort() method.
default void sort(Comparator<? super E> c) {
Object[] a = this.toArray();
Arrays.sort(a, (Comparator) c);
ListIterator<E> i = this.listIterator();
for (Object e : a) {
i.next();
i.set((E) e);
}
}As can be seen from the above source code, the functions of the sort() method are as follows:
- The whole sort() method will first pass in a Comparator comparator as a parameter, which is used as the comparison standard;
- Then it will convert the list Object into an Object array and use arrays The sort () method sorts the array;
- After sorting, use the iterator to change the contents of the list collection again.
Therefore, the sorting function of the List#sort() method mainly depends on arrays Sort () method, so we need to continue to find out arrays How to implement the sort () method? Its source code is as follows:
public static <T> void sort(T[] a, Comparator<? super T> c) {
if (c == null) {
sort(a);
} else {
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, c);
else
TimSort.sort(a, 0, a.length, c, null, 0, 0);
}
}Arrays. The main execution logic of sort () method is as follows:
- First, if/else branching will be judged in the sort() method. There are two cases according to whether the Comparator object is empty.
- When the Comparator object is empty, the internal sort() method will be called;
- When legacymergesort When userrequested is true, legacyMergeSort() will be used for sorting; otherwise, timsort. Will be used Sort sort.
3. Introduction to merging and sorting
LegacyMergeSort method is actually a merge sort provided in JDK 7 for compatibility with previous versions, while TimSort is an optimized merge sort.
The so-called merge sort here is an effective and stable sorting algorithm based on merge operation. The algorithm adopts the divide and conquer idea. Its idea is to merge the sorted subsequences to obtain a completely ordered sequence. In other words, the algorithm will first sort each subsequence, and finally merge the two ordered tables into an ordered table, which is called two-way merging.
The core principle of merge sort is to divide an array into two sub arrays, sort each sub array, and finally merge. When each array is sorted, it will compare and exchange between two adjacent elements, and the relative position of the same element will not change. It is a stable algorithm.
4. Analysis of legacymergesort () method source code
Since the legacyMergeSort() method is invoked in the Arrays#sort() method, we also need to look at the source code of the method.
private static <T> void legacyMergeSort(T[] a, Comparator<? super T> c) {
//Define a new array for use after sorting
T[] aux = a.clone();
if (c==null)
mergeSort(aux, a, 0, a.length, 0);
else
mergeSort(aux, a, 0, a.length, 0, c);
}
private static void mergeSort(Object[] src,
Object[] dest,
int low, int high, int off,
Comparator c) {
int length = high - low;
//If the array length is less than 7, insert sort is used,
//That is, each element is compared with the element in front of it one by one. If it is smaller than the previous element, the positions of the two are exchanged.
// Insertion sort on smallest arrays
if (length < INSERTIONSORT_THRESHOLD) {
for (int i=low; i<high; i++)
for (int j=i; j>low && c.compare(dest[j-1], dest[j])>0; j--)
swap(dest, j, j-1);
return;
}
// Here, the idea of divide and conquer is used to split and recursively call insertion sorting.
// Here, the array to be sorted is divided into two, and the score group is continuously cut by using the idea of recursion,
// When the length of the segmented array is less than 7, insert sorting is still used for sorting, and then merge to complete the sorting function.
// Recursively sort halves of dest into src
int destLow = low;
int destHigh = high;
low += off;
high += off;
int mid = (low + high) >>> 1;
mergeSort(dest, src, low, mid, -off, c);
mergeSort(dest, src, mid, high, -off, c);
//Merge two adjacent arranged arrays. If the maximum value on the left is less than the minimum value on the right, it means that the array has been arranged and copied directly
// If list is already sorted, just copy from src to dest. This is an
// optimization that results in faster sorts for nearly ordered lists.
if (c.compare(src[mid-1], src[mid]) <= 0) {
System.arraycopy(src, low, dest, destLow, length);
return;
}
//Merge and sort here
// Merge sorted halves (now in src) into dest
for(int i = destLow, p = low, q = mid; i < destHigh; i++) {
if (q >= high || p < mid && c.compare(src[p], src[q]) <= 0)
dest[i] = src[p++];
else
dest[i] = src[q++];
}
} 5. TimSort.sort() method source code
In arrays In the sort () method, when the system detects that it is a new version of JDK, it will call timsort Sort() method. The source code is as follows:
static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
T[] work, int workBase, int workLen) {
assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;
//Get the number of elements of the array to be sorted. If the number is less than 2, there is no need to sort.
int nRemaining = hi - lo;
if (nRemaining < 2)
return; // Arrays of size 0 and 1 are always sorted
//If the passed in array to be sorted is less than the threshold min_ Merge (32 in Java implementation and 64 in Python Implementation),
//Then binarySort is called, which is a mini timsort that does not contain merge operations. It is an optimized binary sort.
// If array is small, do a "mini-TimSort" with no merges
if (nRemaining < MIN_MERGE) {
int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
//Using the binary search method, insert the subsequent numbers into the previously sorted array, and binarySort sorts the array a[lo:hi],
//And a[lo:start] is already ordered.
binarySort(a, lo, hi, lo + initRunLen, c);
return;
}
//When executing the binarySort method, you need to insert the number after lo + initRunLen into the previous ascending sequence.
//If the array to be sorted is greater than the threshold MIN_MERGE, sort directly.
/**
* March over the array once, left to right, finding natural runs,
* extending short natural runs to minRun elements, and merging runs
* to maintain stack invariant.
*/
TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);
int minRun = minRunLength(nRemaining);
do {
// Identify next run
int runLen = countRunAndMakeAscending(a, lo, hi, c);
// If run is short, extend to min(minRun, nRemaining)
if (runLen < minRun) {
int force = nRemaining <= minRun ? nRemaining : minRun;
binarySort(a, lo, lo + force, lo + runLen, c);
runLen = force;
}
// Push run onto pending-run stack, and maybe merge
ts.pushRun(lo, runLen);
ts.mergeCollapse();
// Advance to find next run
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0);
// Merge all remaining runs to complete sort
assert lo == hi;
ts.mergeForceCollapse();
assert ts.stackSize == 1;
}TimSort algorithm is a hybrid sorting algorithm originated from merge sorting and insert sorting. It was originally proposed by Tim Peters in Python language in 2002, mainly to make various data in the real world have better performance.
TimSort does a lot of optimization on merge sort, optimizes the input performance of reverse sort in merge sort, and reduces backtracking for the input of forward sort.
The core idea of TimSort is actually partitioning and merging.
Partition: scan the array once and turn its internal elements into a continuous positive sequence (positive sequence is ascending). If it is an inverse sequence, the elements in the partition are reversed. For example, divide 1, 2, 3, 6, 4, 5, 8, 6 and 4 into [1,2,3,6], [4,5,8], [6,4], and then reverse, [1,2,3,6], [4,5,8], [4,6]
Merge: use a strategy to optimize the merge order.
The above is a brief introduction to the source code of the Arrays#sort() method. You can simply understand it. So far, brother Yi will take you to sort the collection with the sort() method. Next, I will explain other sorting methods in the next article. Please pay attention.