Tip from the front row: Although this algorithm is nominally a standard RMQ, it is not as simple as st table, line segment tree and other algorithms / data structures. It can even achieve a good RMQ algorithm with a smaller constant than the line segment tree but without repair only by hard jumping of Cartesian tree.
CSP-S preliminary
When I saw the last question in the examination room:
-
Cartesian tree, OK, I wrote it
-
LCA, OK, yes
-
Eulerian order, OK, I've written it many times
-
ST watch, okay, it's engraved in DNA
-
Block, emmm... Reluctantly
-
\(\ pm 1\)RMQ... I regret not learning the LCA of \ (< \ theta (n), \ theta (1) > \)
So I made it up quickly after the game.
Let's see what rmqs are available first
-
Naive algorithm \ (< \ mathrm {o} (n) > \)
-
st table \ (< \ mathrm {o} (n \ log n), \ mathrm {o} (1) > \)
-
Four Russian \(<\mathrm{O}(n \log \log n),\mathrm{O}(1)>\)
-
Sqrt tree \ (< \ mathrm {o} (n \ log \ log n), \ mathrm {o} (1) > \) and supports \ (\ mathrm{O}(\sqrt{n}) \) modification
-
Segment tree \ (< \ mathrm {o} (n), \ mathrm {o} (\ log n) > \)
-
Cat tree \ (< \ mathrm {o} (n \ log n), \ mathrm {o} (1) > \)
-
Turn Cartesian tree and multiply LCA \ (< \ mathrm {o} (n \ log n), \ mathrm {o} (\ log n) > \)
-
Turn to Cartesian tree and then split the tree into LCA \ (< \ mathrm {o} (n), \ mathrm {o} (\ log n) > \)
-
Turn to Cartesian tree and jump down from the root node \ (< \ mathrm {o} (n), \ mathrm {o} (?) > \)
-
Standard RMQ \ (< \ mathrm {o} (n), \ mathrm {o} (1) > \)
Look at an example
emmm this \ (< \ theta (n \ log n), \ theta (1) > \) can pass. Why choose this?
Because the optimal solution of this problem is not as good as this one, not all Four Russian
Well, let's have a more exciting one.
Why did you see the Swedish forklift? Is it in the river
The meaning of the question is to give you an extraordinary linear congruence random number generator
I won't talk about linear congruence and Mason winder (mt19937 of c++11).
Anyway, it uses the random seed input to you to generate many random numbers. If you study the linear congruence, you will know that this thing is really random (but it still can't meet the algorithm with too high requirements for random numbers such as Monte Carlo). It seems that you can't mess with mathematical knowledge.
Then look at the data range
......
............
..................
2e7..................
First of all, it can be said that the st table has been climbed. Not all four Russians (equivalent to opening three st tables, the constant is slightly larger, and the complexity \ (< \ mathrm {o} (n \ log \ log n) >, \ theta (1) \)) can also be climbed. Let alone the query of segment tree with \ (\ log \).
So we came to the main play.
First think about what algorithm is \ (< \ theta (n), \ theta (1) > \).
TarjanLCA? It doesn't matter.
\(\pm 1\)RMQ? This is indeed RMQ, but it is conditional that the difference between two adjacent numbers is 1.
This RMQ can calculate the LCA online, because the two adjacent elements in the Euler sequence must be the relationship between the parent node and the child node, and the depth difference is 1
Therefore, consider turning the RMQ tree of the interval into LCA
In case of indecision, the problem is offline / on the tree
Then it's Descartes tree's turn
P5854 [template] Cartesian tree
This picture stolen from oi wiki can best let you understand the nature of Cartesian tree.
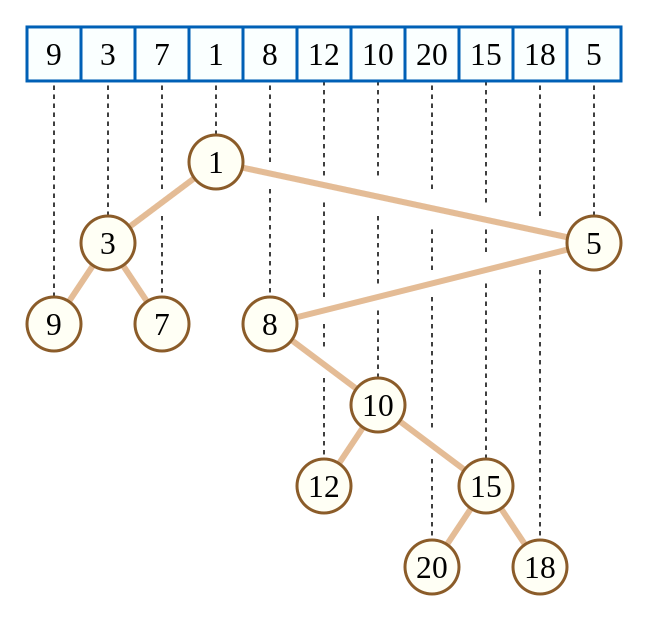
It can be found that in this figure, the minimum value of the query interval is transformed into the LCA of two nodes, and the process of constructing Cartesian tree using monotone stack is \ (\ mathrm{O}(n) \), which is really great.
Now consider LCA.
P3379 [template] nearest common ancestor (LCA)
Offline TarjanLCA can do linear preprocessing, \ (\ Theta(1) \) answer each query, which obviously can solve the above example.
Let's be more demanding and consider the practice of online query.
Now it's time to choose how to do LCA.
-
Multiplication on the tree, 80% of oiers are the first to learn the LCA method of non naive algorithm \ (< \ mathrm {o} (n \ log n), \ mathrm {o} (\ log n) > \)
-
Tarjan, an off-line algorithm using parallel search set
-
Tree section, small constant, clear logic, very easy to write \ (< \ theta (n), \ mathrm {o} (\ log n) > \)
-
Convert to Euler order and then do RMQ. Well, we successfully detour back to the original problem. The complexity depends on the RMQ algorithm selected
In order not to make the problem recursive, we need to find a combined algorithm for finding RMQ for Euler sequences.
According to the definition, the depth of two nodes in the node between the first occurrence position of the sequence is the smallest. That is, the comparison keyword is depth, but the sequence is node.
So consider the nature of depth on Euler order
Euler sequence is constructed by adding it to the end of the sequence when searching and tracing back to a node in the process of DFS.
Therefore, it can be found that if the previous node of the sequence searches its child node or traces back to its parent node to get the next node of the sequence, the depth between the two must be 1.
Each node will be recorded many times, but according to the progressive and extreme thinking, our complexity is still linear, so don't panic, hahaha
At this time, the previous Four Russian comes again. The bottleneck of the complexity of this algorithm lies in the post-processing of the parts in the block, plus the constraints with a difference of 1. Usually, this algorithm is called:
\(\pm 1\)RMQ
Here comes the trouble.
Block first.
Make the block length \ (b = \lceil \frac{\log n}{2} \rceil \)
Therefore, the st table is used to query the whole block. The initialization complexity \ (\ Theta(n) \) complexity is very excellent. There is no panic. As the saying goes, no matter how many layers of O(n) or linearity are stacked
Therefore, there are \ (\ frac{\log n}{2} \) in each block. Considering the characteristic that the difference is 1, a left endpoint is directly fixed. For all the right endpoints in the block, the violence table can be created by looking up the table during query. The constant is so large that the explosion is too convenient for violence preprocessing.
So the problem was solved.
The code can even refer to this year's preliminary competition directly.
summary
The whole process of RMQ is:
The random RMQ is transformed into LCA through Cartesian tree
The LCA is transformed into RMQ with \ (\ pm 1 \) constraints through Euler sequence
The RMQ of Euler order is solved by blocking and Four Russian
To obtain LCA is to obtain the interval maximum of the original sequence
It's not over yet
You can find that the space occupied by this standard RMQ is very. If you put it in the previous example, it will be MLE, so how to cut off the problem of saving grandpa from you?
Still consider Cartesian trees.
This tree is a binary tree, so consider jumping down from the root node to the covered interval, which is just within the query interval. In addition, the data is random and the depth is no more than \ (\ log n \), so you can just mess around directly.
code
namespace RMQ {
constexpr int N = 100005;
constexpr int MT = N << 1;
constexpr int L = 20,B = 9,C = MT / B;
struct Node {
int val;
int dep,dfn,end;
Node *son[2];
}T[N];
Node *min(Node *x, Node *y) {
return x -> dep < y -> dep ? x : y;
}
int n,dfs_clock,b,c;
int pos[(1 << (B - 1)) + 5], dif[C + 5];
Node *r,*A[MT],*Min[L][C];
void build() {
static Node *S[N];
int top = 0;
repl(i,0,n) {
Node *p = &T[i];
while(top && S[top] -> val < p -> val)
p -> son[0] = S[top--];
if(top) S[top] -> son[1] = p;
S[++top] = p;
}
r = S[1];
}
void dfs(Node *u) {
A[u -> dfn = dfs_clock++] = u;
rep(i,0,1) if(u -> son[i]) {
u -> son[i] -> dep = u -> dep + 1;
dfs(u -> son[i]);
A[dfs_clock++] = u;
}
u -> end = dfs_clock - 1;
}
void init_st() {
b = (int)(ceil(log2(dfs_clock) / 2));
c = dfs_clock / b;
repl(i,0,c) {
Min[0][i] = A[b * i];
repl(j,1,b) Min[0][i] = min(Min[0][i],A[i * b + j]);
}
for (register int i = 1,l = 2;l <= c;++i,l <<= 1)
for (register int j = 0; j + l <= c;++j)
Min[i][j] = min(Min[i - 1][j], Min[i - 1][j + (l >> 1)]);
}
void init_block() {
rep(i,0,c)
for(register int j = 1;j < b && i * b + j < dfs_clock;++j)
if(A[i * b + j] -> dep < A[i * b + j - 1] -> dep)
dif[i] |= 1 << (j - 1);
repl(i,0,(1 << (b - 1))) {
int mx = 0,v = 0;
ff(j,1,b - 1) {
v += (i >> (j - 1) & 1) ? -1 : 1;
if(v < mx) {
mx = v;
pos[i] = j;
}
}
}
}
void init(int len) {
n = len;
build();
dfs(r);
init_st();
init_block();
}
#define l2(x) (31 - __builtin_clz(x))
Node *query_ST(int L,int R) {
int k = l2(R - L + 1);
return std::min(Min[k][L], Min[k][R - (1 << k) + 1]);
}
Node *query_block(int L,int R) {
int p = L / b;
int s = (dif[p] >> (L - p * b)) & ((1 << (R - L)) - 1);
return A[L + pos[s]];
}
Node *query(int L,int R) {
L = T[L].dfn,R = T[R].dfn;
if(L > R) std::swap(L,R);
int pl = L / b,pr = R / b;
if(pl == pr) return query_block(L,R);
Node *s = std::min(query_block(L, pl * b + b - 1),query_block(pr * b, R));
if(pl + 1 <= pr - 1) s = std::min(s,query_ST(pl + 1,pr - 1));
return s;
}
}