[Huawei machine test of Niuke network] HJ28 prime partner

subject

describe

Title Description
If the sum of two positive integers is prime, the two positive integers are called "prime partners", such as 2 and 5, 6 and 13, which can be applied to communication encryption. Now the society of cryptography asks you to design a program to select several pairs from the existing N (N is an even number) positive integers to form a "prime partner". There are various selection schemes. For example, there are four positive integers: 2, 5, 6 and 13. If you divide 5 and 6 into a group, you can only get one group of "prime partners", while grouping 2 and 5, 6 and 13 will get two groups of "prime partners", The scheme that can form the most "prime partners" is called the "best scheme". Of course, the cryptography society hopes you to find the "best scheme".

Input:

There is a positive even number N (N ≤ 100), which represents the number of natural numbers to be selected. Specific figures are given later, ranging from [230000].

Output:

Output an integer K, indicating the logarithm of the "prime partner" composed of the "best solution" you obtained.

Enter Description:

Enter description
one   Enter a positive even number n
two   Enter n integers
Note: there may be multiple groups of data

Output Description:

The "best plan" obtained constitutes the logarithm of the "prime partner".

Example 1

Input:

4
2 5 6 13
2
3 6

Output:

2
0

Problem solving ideas

(1) Even numbers plus even numbers have a common factor of 2, so even numbers and even numbers must not be prime numbers

(2) First, divide the input numbers into parity

def group_lst(lst): ##Partial parity
    a, b = [], []
    for i in lst:
        if int(i) % 2 == 0:
            a.append(int(i))
        else:
            b.append(int(i))
    return a, b

(2) Judge whether it is a prime number: HJ6 prime factor

def prime_judge(n):
    m = int(n ** 0.5) + 2
    for i in range(3, m, 2):
        if n % i == 0:
            return False
    return True

(3) Construct a matrix l record, record the result of odd and even pairwise addition, mark the result with prime number as 1, and the rest as 0

def matrix_ab(a, b):
    l = [[0 for _ in b] for _ in a]
    for ii, i in enumerate(a):
        for jj, j in enumerate(b):
            if prime_judge(i + j):
                l[ii][jj] = 1
    return l

(4)a = [5, 13]，b = [2, 6]

513
210
611

(5) Write recursive function find and use Hungarian algorithm to find the optimal combination

def find(x):
    for index in range(len(b)):
        if matrix[x][index] == 1 and used_b[index] == 0:
            used_b[index] = 1
            if conection_b[index] == -1 or find(conection_b[index]) != 0:
                conection_b[index] = x
                return 1
    return 0

(6) Sample analysis of execution steps of find function

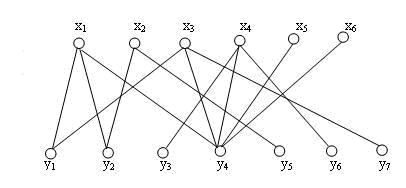
  According to the corresponding relationship between x and y in the figure above, the following matrix can be constructed

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010
x50001000
x60001000

(7) The outermost loops x1 to x6, i.e. the first line to the sixth line, are traversed from y1 to y7 respectively

(8) Where used_b = [0, 0, 0, 0, 0, 0, 0] is y1 used in a row

(9)conection_b = [-1,-1,-1,-1,-1,-1,-1], where the value range of each element is 0-5, representing the row x corresponding to y

(10) Starting from the first line, y1, conection is selected_ B changes [0, - 1, - 1, - 1, - 1, - 1, - 1, - 1]

i: 0
find: 0
_index: 0
_used_b: [1, 0, 0, 0, 0, 0, 0]
_conection_b: [-1, -1, -1, -1, -1, -1, -1]
index: 0
conection_b: [0, -1, -1, -1, -1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000

(11) In the second row, y2, conection is selected_ B changes [0, 1, - 1, - 1, - 1, - 1, - 1]

i: 1
find: 1
_index: 1
_used_b: [0, 1, 0, 0, 0, 0, 0]
_conection_b: [0, -1, -1, -1, -1, -1, -1]
index: 1
conection_b: [0, 1, -1, -1, -1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000
x20100100

(11) In the third row, y1 is selected. Since y1 is also selected in the first row, recursion is entered

i: 2
find: 2
_index: 0
_used_b: [1, 0, 0, 0, 0, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
find: 0
_index: 1
_used_b: [1, 1, 0, 0, 0, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
find: 1
_index: 4
_used_b: [1, 1, 0, 0, 1, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
index: 4
conection_b: [0, 1, -1, -1, 1, -1, -1]
index: 1
conection_b: [0, 0, -1, -1, 1, -1, -1]
index: 0
conection_b: [2, 0, -1, -1, 1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000
x20100100
x31001001

(12) Get that the index of the conflicting row is 0, so start finding (0), and find that y2 is also used, so continue to recursively find(1)

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001

(13) Finally x2 finds y5, so the recursion ends_ b: [2, 0, -1, -1, 1, -1, -1]

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001

(14) In the fourth row, y3 is selected. Since there is no conflict, there is no conflict_ b: [2, 0, 3, -1, 1, -1, -1]

i: 3
find: 3
_index: 2
_used_b: [0, 0, 1, 0, 0, 0, 0]
_conection_b: [2, 0, -1, -1, 1, -1, -1]
index: 2
conection_b: [2, 0, 3, -1, 1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010

(14) In the fifth row, y4 is selected. Since there is no conflict, there is no conflict_ b: [2, 0, 3, 4, 1, -1, -1]

i: 4
find: 4
_index: 3
_used_b: [0, 0, 0, 1, 0, 0, 0]
_conection_b: [2, 0, 3, -1, 1, -1, -1]
index: 3
conection_b: [2, 0, 3, 4, 1, -1, -1]
count
y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010
x50001000

(14) In the sixth row, y4 is selected. Because it conflicts with the fifth row, it enters recursive find(4)

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010
x50001000
x60001000
i: 5
find: 5
_index: 3
_used_b: [0, 0, 0, 1, 0, 0, 0]
_conection_b: [2, 0, 3, 4, 1, -1, -1]
find: 4
used_b: [0, 0, 0, 1, 0, 0, 0]
conection_b: [2, 0, 3, 4, 1, -1, -1]
5

(15) Because there are no other optional line items except y4 in the fifth row, so   find(4) = 0，conection_b has not been changed, so: conection_b: [2, 0, 3, 4, 1, -1, -1]

y1y2y3y4y5y6y7
x11101000
x20100100
x31001001
x40011010
x50001000
x60001000
>>>def find(x):
...    print("find:", x)
...    for index in range(7):
...        if matrix[x][index] == 1 and used_b[index] == 0:
...            used_b[index] = 1
...            print("_index:", index)
...            print("_used_b:", str(used_b))
...            print("_conection_b:", str(conection_b))
...            if conection_b[index] == -1 or find(conection_b[index]) != 0:
...                print("index:", index)
...                conection_b[index] = x
...                print("conection_b:", str(conection_b))
...                return 1
...    return 0
>>>matrix = [
...    [1,1,0,1,0,0,0],
...    [0,1,0,0,1,0,0],
...    [1,0,0,1,0,0,1],
...    [0,0,1,1,0,1,0],
...    [0,0,0,1,0,0,0],
...    [0,0,0,1,0,0,0]
...    ]
>>>conection_b = [-1 for _ in range(7)]
>>>count = 0
>>>for i in range(6):
...    used_b = [0 for _ in range(7)]
...    print("i:",i)
...    if find(i):
...        print("count")
...        count += 1
>>>print("used_b:", str(used_b))
>>>print("conection_b:", str(conection_b))
>>>print(count)
i: 0
find: 0
_index: 0
_used_b: [1, 0, 0, 0, 0, 0, 0]
_conection_b: [-1, -1, -1, -1, -1, -1, -1]
index: 0
conection_b: [0, -1, -1, -1, -1, -1, -1]
count
i: 1
find: 1
_index: 1
_used_b: [0, 1, 0, 0, 0, 0, 0]
_conection_b: [0, -1, -1, -1, -1, -1, -1]
index: 1
conection_b: [0, 1, -1, -1, -1, -1, -1]
count
i: 2
find: 2
_index: 0
_used_b: [1, 0, 0, 0, 0, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
find: 0
_index: 1
_used_b: [1, 1, 0, 0, 0, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
find: 1
_index: 4
_used_b: [1, 1, 0, 0, 1, 0, 0]
_conection_b: [0, 1, -1, -1, -1, -1, -1]
index: 4
conection_b: [0, 1, -1, -1, 1, -1, -1]
index: 1
conection_b: [0, 0, -1, -1, 1, -1, -1]
index: 0
conection_b: [2, 0, -1, -1, 1, -1, -1]
count
i: 3
find: 3
_index: 2
_used_b: [0, 0, 1, 0, 0, 0, 0]
_conection_b: [2, 0, -1, -1, 1, -1, -1]
index: 2
conection_b: [2, 0, 3, -1, 1, -1, -1]
count
i: 4
find: 4
_index: 3
_used_b: [0, 0, 0, 1, 0, 0, 0]
_conection_b: [2, 0, 3, -1, 1, -1, -1]
index: 3
conection_b: [2, 0, 3, 4, 1, -1, -1]
count
i: 5
find: 5
_index: 3
_used_b: [0, 0, 0, 1, 0, 0, 0]
_conection_b: [2, 0, 3, 4, 1, -1, -1]
find: 4
used_b: [0, 0, 0, 1, 0, 0, 0]
conection_b: [2, 0, 3, 4, 1, -1, -1]
5

summary

The core idea of the Hungarian algorithm is: give priority to the last row. If there is a conflict, look for the replaceable item of the conflicting row. If there is no replaceable item, discard the last row. If there is a replaceable item, use it for substitution. If there is a conflict after substitution, enter recursion. If it is found that the conflict cannot be resolved, discard the last row and the conflict can be resolved, Use this scheme.

code

def prime_judge(n):
    m = int(n ** 0.5) + 2
    for i in range(3, m, 2):
        if n % i == 0:
            return False
    return True
   
def group_lst(lst): ##Partial parity
    a, b = [], []
    for i in lst:
        if int(i) % 2 == 0:
            a.append(int(i))
        else:
            b.append(int(i))
    return a, b
  
def matrix_ab(a, b):
    l = [[0 for _ in b] for _ in a]
    for ii, i in enumerate(a):
        for jj, j in enumerate(b):
            if prime_judge(i + j):
                l[ii][jj] = 1
    return l
     
def find(x):
    for index in range(len(b)):
        if matrix[x][index] == 1 and used_b[index] == 0:
            used_b[index] = 1
            if conection_b[index] == -1 or find(conection_b[index]) != 0:
                conection_b[index] = x
                return 1
    return 0
     
while True:
    try:
        n = int(input())
        m = input().split(' ')
        a, b = group_lst(m)
        matrix = matrix_ab(a, b)
        conection_b = [-1 for _ in range(len(b))]
        count = 0
        for i in range(len(a)):
            used_b = [0 for _ in range(len(b))]
            if find(i):
                count += 1
        print(count)
    except:
        break

Reference

https://www.nowcoder.com/ta/huawei/

https://blog.csdn.net/weixin_37474682/article/details/119899324

Keywords: Python Algorithm leetcode Interview cryptology

Added by wdseelig on Mon, 06 Sep 2021 02:37:37 +0300

Popular Keywords

©2024 Programming VIP