hznuoj topic
[C series synthesis 1] game master I
Description
ydw of ACM team is a game enthusiast. He likes to play all kinds of stand-alone games and is happy to get all kinds of endings. However, due to the limited time (he also has to issue TAT), he can only choose a few endings he likes to pass. Because ydw is a game expert, he can handle all the plot by himself without checking the strategy, However, due to self-reliance, the time to complete each ending is different, and his preference for each ending is also different, that is, he gets different pleasure from each ending. He hopes to pass some endings in his limited time to maximize his pleasure.
Input
There are multiple sets of test data,
The first behavior N (0 < N < = 100) and t (0 < T < = 2000) means ydw there are N games to play, and the total time to play the game is t.
In the next 3*N lines, the first number n (1 < = n < = 10) in each line indicates that there are several endings of the game. In the next line, n numbers represent the pleasure that can be obtained by passing a certain ending ydw, and then n numbers in the next line represent the time required for ydw to pass a certain ending.
Test data ends with 0. (the data ensure that the pleasure degree and time are greater than 0 and less than or equal to 1000)
Output
The greatest pleasure that ydw can get.
Samples
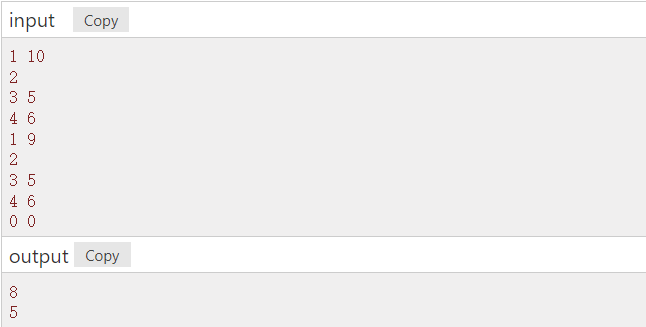
Problem solving methods learn from [dynamic programming] 01 knapsack problem (easy to understand, super basic explanation)
https://blog.csdn.net/qq_38410730/article/details/81667885Topic analysis
General idea
Break big problems into small ones
Solution
Simplify the question: there are m endings. After each ending, you can get h points of pleasure and consume t points of time. There is a total of t time. Ask how much pleasure you can get at most.
happy[i] is defined as the degree of pleasure that can be obtained for each outcome
time[i] is the time to be consumed for each ending
Definition H(i,j): the current remaining time j, the maximum pleasure that the first i outcomes can bring
When the time required for the i-th ending is greater than the remaining available time
H(i,j) = H(i-1,j) // I can't play the i-th ending
When the time required for the ith ending is less than or equal to the remaining available time
H(i,j) = H(i-1,j) // Don't play the i-th ending
Or H(i,j) = H(i - 1,j - t[i]) + h[i] // Play the i-th ending (the two schemes use the one with more pleasure)
It can be analyzed with the help of charts
(the example data is h (2, 3, 4) t (1, 4, 3)) t is 7
For example, i=1, j=1, t(1)=1, h(1)=2, there is j=t(1), so H(1,1)=max {H(1-1,1), H(1-1,2-t(1))+h(1)} = 2;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2 | 0 | 2 | 2 | 2 | 3 | 5 | 5 | 5 |
| 3 | 0 | 2 | 2 | 4 | 6 | 6 | 6 | 7 |
After a general understanding of the principle, start solving the problem.
Problem solving structure
1. Define a structure to store the pleasure required for each outcome of each game, as follows:
struct game{
int happy[100];
int time[100];
int type;
}g[110];2. Define another structure to store the information of each outcome, as follows:
struct res{ //Used to receive data for all types of outcomes
int happy;
int time;
}r[11000];3. Define chart
int charm[1010][2010]={{0}};//Define dynamic planning table 4. Define a max function
int Max(int x,int y){ //Define a function that returns a larger value
return x>y?x:y;
} 5. Enter the data required by the topic
int N,T;
int n;
int H=0; //Record how much pleasure you can get in total
while(scanf("%d %d",&N,&T),(N||T)){ //Enter N games, total T time
for(int i=0;i<N;i++){ //Enter n endings for each game
scanf("%d",&g[i].type);
for(int j=0;j<g[i].type;j++) //Enter the pleasure of n outcomes
scanf("%d",&g[i].happy[j]);
for(int j=0;j<g[i].type;j++) //Enter the time required for n outcomes
scanf("%d",&g[i].time[j]);
}
}6. Copy the input value into the res structure to facilitate the planning of all outcomes of each game
int m=1;
r[0].happy=0;
r[0].time=0;
for(int i=0;i<N;i++){
//Copy the data of each outcome to the res structure
for(int j=0;j<g[i].type;j++){
r[m].happy=g[i].happy[j];
r[m].time=g[i].time[j];
m++;
}
}7. Start dynamic allocation
//m is the total number of all outcomes
/*Dynamic planning time allocation from r[1].happy~r[m].happy is the degree of pleasure that can be obtained for each outcome
r[1].time ~r[m]. time Is the time required for each ending */
//Dynamic planning table size should be (m+1)*(T+1)
for (int i=1;i<=m;i++) {
for (int j=1;j<=T;j++) {
if (j<r[i].time)
charm[i][j] = charm[i-1][j];
else
charm[i][j] = Max(charm[i-1][j], charm[i-1][j-r[i].time] + r[i].happy);
}
}
H=charm[m][T];8. Final printing results
printf("%d\n",H);All codes:
#include<stdio.h>
int charm[1010][2010]={{0}};//Define dynamic planning table
int Max(int x,int y){ //Define a function that returns a larger value
return x>y?x:y;
}
struct game{
int happy[100];
int time[100];
int type;
}g[110];
struct res{ //Used to receive data for all types of outcomes
int happy;
int time;
}r[11000];
int main()
{
int N,T;
int n;
int H=0; //Record how much pleasure you can get in total
while(scanf("%d %d",&N,&T),(N||T)){ //Enter N games, total T time
for(int i=0;i<N;i++){ //Enter n endings for each game
scanf("%d",&g[i].type);
for(int j=0;j<g[i].type;j++) //Enter the pleasure of n outcomes
scanf("%d",&g[i].happy[j]);
for(int j=0;j<g[i].type;j++) //Enter the time required for n outcomes
scanf("%d",&g[i].time[j]);
}
int m=1;
r[0].happy=0;
r[0].time=0;
for(int i=0;i<N;i++){
//Copy the data of each outcome to the res structure
for(int j=0;j<g[i].type;j++){
r[m].happy=g[i].happy[j];
r[m].time=g[i].time[j];
m++;
}
}
m--;
/*Dynamic planning time allocation from r[0].happy~r[m].happy is the degree of pleasure that can be obtained for each outcome
r[0].time ~r[m]. time Is the time required for each ending */
//Dynamic planning table size should be (m+1)*(T+1)
for (int i=1;i<=m;i++) {
for (int j=1;j<=T;j++) {
if (j<r[i].time)
charm[i][j] = charm[i-1][j];
else
charm[i][j] = Max(charm[i-1][j], charm[i-1][j-r[i].time] + r[i].happy);
}
}
H=charm[m][T];
printf("%d\n",H);
}
return 0;
}