1, Libraries needed

import turtle
import math

The turtle library is used to draw graphics, and the math library is mainly used to determine the equation of graphics

2, Graphic analysis

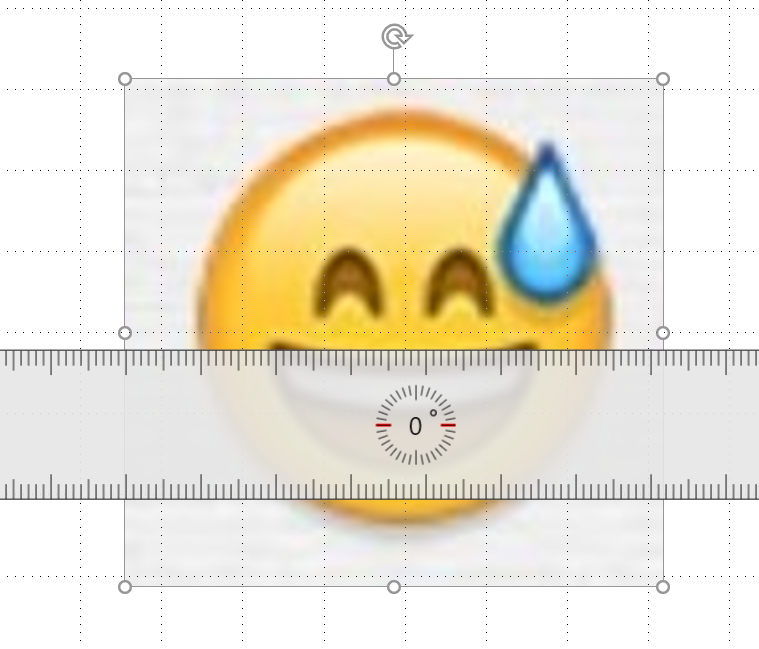
The whole figure consists of outline, eyes, mouth and sweat drops. It can be seen that the outline is a circle; The upper part of the eye is a semi ellipse and the lower part is a semicircle; The upper part of the mouth is an arc, and the lower part is a semicircle; The sweat drop can be regarded as a 240 degree circle and two tangent lines at the end.
Here, I set the radius of the whole contour to 100 pixels and the center of the circle to (0, 0). Use the ruler tool in ppt (in the Drawing toolbar) to measure the proportion of each part, calculate the length, determine the coordinates and start drawing. I won't show my measurement results here (it's written in a mess), but it's reflected in the code. You can measure it yourself.

3, Draw code analysis
First, the overall size of the graph is about 200 × 200 or so, so set the canvas size to 400 × four hundred

turtle.setup(400, 400)

3.1 outline drawing
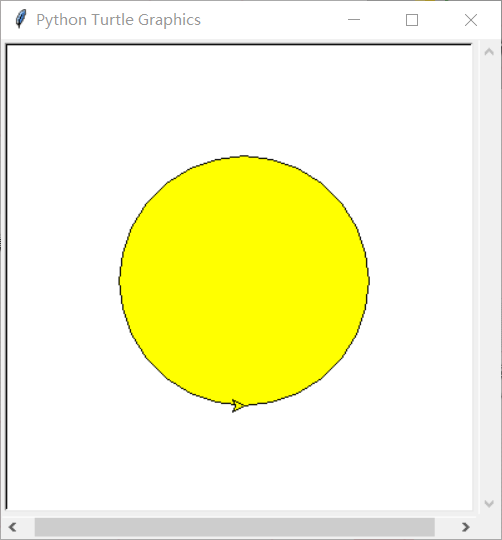
The outline is a circle. There's nothing to say. The circle() function in turtle can be used to draw a circle. It is worth noting that the circle function starts from the bottom of the circle, so let's set the center of the circle to (0,0):

# Set the center point to (0,0)
turtle.penup()
turtle.sety(-100)
turtle.pendown()

Then you can start to draw a circle: the main thing here is that the filling pattern should be in_ The fill() function starts with end_ End of fill() function

# Draw a yellow circle
turtle.begin_fill()
turtle.fillcolor('yellow')
turtle.circle(100)
turtle.end_fill()

The result of the circle drawn is shown in the figure below:

3.2 drawing of eyes
As mentioned earlier, the upper part of the eye is an ellipse, so if you want to draw the eye, you have to solve the problem of drawing an ellipse.
From the mathematics of grade two in primary school, we know that the parametric equation of ellipse is:

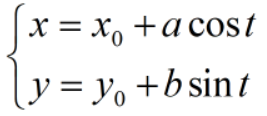
Therefore, to draw an ellipse, we need to know the coordinates of the center of the circle (x,y) and the length of the long and short semi axes a and B. in Python, I choose to draw a flat n-sided shape. As long as n is large enough, an ellipse can be formed, so we also need to know the number of sides n. with these five parameters, we first define a function to draw a half ellipse. The number of sides is temporarily set to 500 and can be increased if necessary (here, set the coordinates of the starting point to (x,y), and it is easy to get that the coordinates of the center of the circle are (x-a, y)):

def half_ellipse(a, b, x, y, n=500):
    """
    Draw half an elliptic function
    :param a: Length of long half shaft
    :param b: Length of short half shaft
    :param n: Number of edges -- n The larger, the closer to the ellipse
    :param x:Abscissa of the starting drawing point
    :param y:Ordinate of the starting drawing point
    """

Then, adjust the brush to the position where you start drawing the semi ellipse:

 turtle.penup()
 turtle.setpos(x, y)  # Location of initial point
 turtle.pendown()

Start drawing according to the parametric equation of the ellipse:

for i in range(n):  # Draw a flat n-sided shape. When n -- > is infinite, the drawn figure is an ellipse
    radian = 2 * math.pi / n  # Divide 2pi radian s into n parts, each of which is radial
    theta = (i + 1) * radian  # Increase radian each time
    next_point = (a * math.cos(theta) + x - a, b * math.sin(theta) + y)
    turtle.setpos(next_point)

Stop halfway through:

if i == n / 2:
    break

The total code of drawing semi elliptic function is as follows:

def half_ellipse(a, b, x, y, n=500):
    """
    Draw half an elliptic function
    :param a: Length of long half shaft
    :param b: Length of short half shaft
    :param n: Number of edges -- n The larger, the closer to the ellipse
    :param x:Abscissa of the starting drawing point
    :param y:Ordinate of the starting drawing point
    """
    turtle.penup()
    turtle.setpos(x, y)  # Location of initial point
    turtle.pendown()
    for i in range(n):  # Draw a flat n-sided shape. When n -- > is infinite, the drawn figure is an ellipse
        radian = 2 * math.pi / n  # Divide 2pi radian s into n parts, each of which is radial
        theta = (i + 1) * radian  # Increase radian each time
        next_point = (a * math.cos(theta) + x - a, b * math.sin(theta) + y)
        turtle.setpos(next_point)
        if i == n / 2:
            break

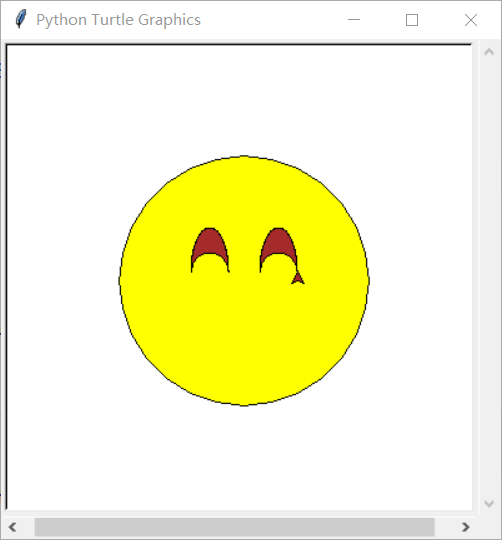
After solving the problem of drawing ellipses, you can start drawing eyes. There is an ellipse above and a circle below. After adjusting the parameters, you can draw them easily:

# Start drawing eyes
# left eye
turtle.begin_fill()
turtle.fillcolor('brown')
half_ellipse(15, 35, -12.5, 7.5)
turtle.seth(-90)
turtle.circle(15, -180)
turtle.end_fill()

Draw the right eye for the same reason. See the source code. The results drawn are as follows:

3.3 drawing of mouth
In fact, the mouth is the most difficult to draw, because the lower part of the mouth is easy, which is a semicircle, but the upper part is difficult to obtain parameters. In ppt, I use a circle to fit, and finally come to the conclusion that the upper part is a circular arc with a radius of 210 pixels and a center angle of 36 degrees.
So just draw these two arcs and fill them with Brown:

# Start drawing your mouth
turtle.begin_fill()
turtle.fillcolor('brown')
turtle.penup()
turtle.setpos(-65, -5)
turtle.pendown()
turtle.seth(-90)
turtle.circle(65, 180)
turtle.seth(18)
turtle.circle(210, -36)
turtle.end_fill()

The result drawn is shown in the figure below. Does it have internal flavor?

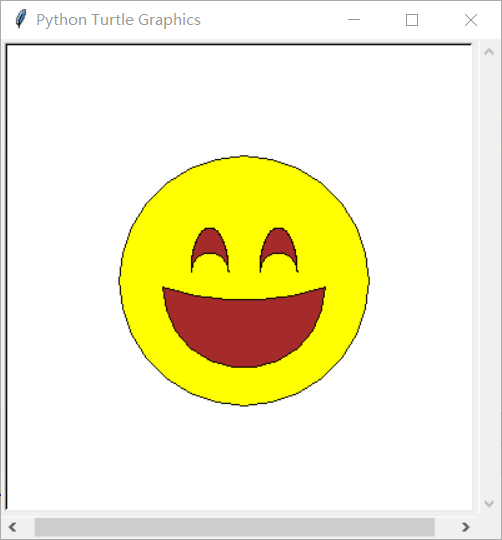
3.4 drawing of sweat drops
The sweat drop is very simple. It is a 240 degree arc plus two tangent lines, which can be drawn easily. The code is as follows:

# Start painting sweat
turtle.begin_fill()
turtle.fillcolor('blue')
turtle.penup()
turtle.setpos(70, 55)
turtle.pendown()
turtle.seth(-120)
turtle.circle(22.5, 240)
turtle.forward(22.5 * math.sqrt(3))
turtle.seth(-120)
turtle.forward(22.5 * math.sqrt(3))
turtle.end_fill()

In this way, a sweating soybean is basically finished. Finally, hide the brush and hover the canvas. It is worth noting that in pycharm, we need to add turtle The line of code done () can make the canvas hover. If you directly use Python's IDLE, you can automatically hover without this line of code

turtle.hideturtle()
turtle.done()

The final effect is as like as two peas below.

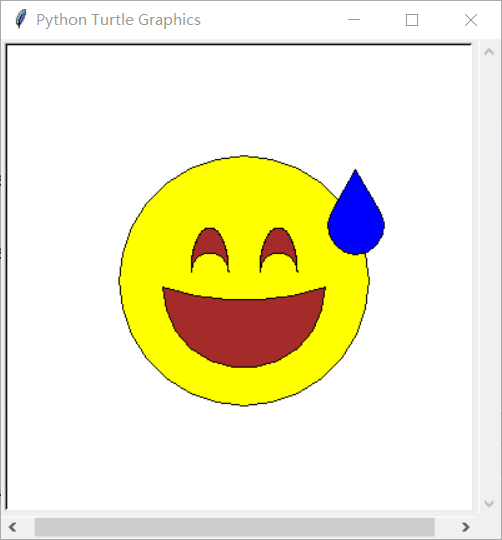
4, Feeling
I'm really in a bad state recently. I'm dizzy with a series of big homework and all kinds of programming. How can there be a course divided into two early eight courses!!! Four credits of probability theory, two early eight, laugh to death, can't get up at all. And the probability theory teacher, I'm really speechless. I call the names twice in a class. If I don't want to give it a normal score, I think, isn't a class for the purpose of learning knowledge? Just look at the exam results. What's the name? So I felt it and wrote this code. There was speechless between the lines. I was really speechless. But after make complaints about this article, I feel much more relaxed. It seems that Tucao is really useful.

5, Source code
Finally, the code for drawing sweating soybeans is integrated into a function. Many places are not well done. If you have comments or suggestions, please come and discuss with me.

import turtle
import math


def half_ellipse(a, b, x, y, n=500):
    """
    Draw half an elliptic function
    :param a: Length of long half shaft
    :param b: Length of short half shaft
    :param n: Number of edges -- n The larger, the closer to the ellipse
    :param x:Abscissa of the starting drawing point
    :param y:Ordinate of the starting drawing point
    """
    turtle.penup()
    turtle.setpos(x, y)  # Location of initial point
    turtle.pendown()
    for i in range(n):  # Draw a flat n-sided shape. When n -- > is infinite, the drawn figure is an ellipse
        radian = 2 * math.pi / n  # Divide 2pi radian s into n parts, each of which is radial
        theta = (i + 1) * radian  # Increase radian each time
        next_point = (a * math.cos(theta) + x - a, b * math.sin(theta) + y)
        turtle.setpos(next_point)
        if i == n / 2:
            break


def draw_liuhanhuangdou():
    turtle.setup(400, 400)
    # Set the center point to (0,0)
    turtle.penup()
    turtle.sety(-100)
    turtle.pendown()

    # Draw a yellow circle
    turtle.begin_fill()
    turtle.fillcolor('yellow')
    turtle.circle(100)
    turtle.end_fill()

    # Start drawing eyes
    # left eye
    turtle.begin_fill()
    turtle.fillcolor('brown')
    half_ellipse(15, 35, -12.5, 7.5)
    turtle.seth(-90)
    turtle.circle(15, -180)
    turtle.end_fill()
    # right eye
    turtle.begin_fill()
    turtle.fillcolor('brown')
    half_ellipse(15, 35, 42.5, 7.5)
    turtle.seth(-90)
    turtle.circle(15, -180)
    turtle.end_fill()

    # Start drawing your mouth
    turtle.begin_fill()
    turtle.fillcolor('brown')
    turtle.penup()
    turtle.setpos(-65, -5)
    turtle.pendown()
    turtle.seth(-90)
    turtle.circle(65, 180)
    turtle.seth(18)
    turtle.circle(210, -36)
    turtle.end_fill()

    # Start painting sweat
    turtle.begin_fill()
    turtle.fillcolor('blue')
    turtle.penup()
    turtle.setpos(70, 55)
    turtle.pendown()
    turtle.seth(-120)
    turtle.circle(22.5, 240)
    turtle.forward(22.5 * math.sqrt(3))
    turtle.seth(-120)
    turtle.forward(22.5 * math.sqrt(3))
    turtle.end_fill()

    # Hide the brush and hover the curtain
    turtle.hideturtle()
    turtle.done()


def main():
    draw_liuhanhuangdou()


if __name__ == '__main__':
    main()