392. Judgment subsequence
1. Title
Given the strings S and t, judge whether s is a subsequence of t.
A subsequence of a string is a new string formed by deleting some (or not deleting) characters from the original string without changing the relative position of the remaining characters. (for example, "ace" is a subsequence of "abcde" and "aec" is not).
Advanced:
If there are a large number of input s, called S1, S2,..., Sk, where k > = 1 billion, you need to check whether they are subsequences of T in turn. In this case, how would you change the code?
Example 1:
Input: s = "abc", t = "ahbgdc" Output: true Example 2: Input: s = "axc", t = "ahbgdc" Output: false
Tips:
- 0 <= s.length <= 100
- 0 <= t.length <= 10^4
- Both strings consist of lowercase characters only.
2. Ideas
This topic is an introductory topic of "editing distance series". For subsequences, we find that we only need to "delete" the original string without considering "add" and "replace"
-
Confirm the meaning of dp[i] array and subscript. dp[i] [j] represents the length of the same subsequence of string t with subscript i - 1 as the end and subscript j - 1 as the end. Note that here is to judge whether s is the subsequence of T, that is, the length of T is greater than or equal to s
-
When confirming the state transition equation, the following two cases should be considered
- if (s.charAt(i - 1) == s,charAt(j)) -- a character found in t also appears in S
- if (s.charAt(i - 1) != s. Charat (J)) -- t to delete an element and continue matching, the element does not need to be displayed, and the deletion only needs to inherit the previous bit directly
-
Initialize dp array. From the recursive formula, we can see that dp[i] [j] depends on dp[i - 1] [j - 1] and dp[i] [j - 1], so dp[0] [0] and dp[i] [0] must be initialized. What is the initialization value? Remember to remember the subscript meaning of dp array when initializing dp array
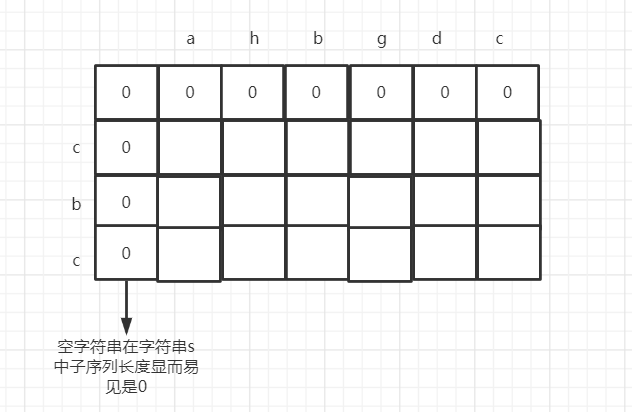
-
Confirm the traversal order. From the state transition equation, dp[i] [j] depends on dp[i - 1] [j - 1] and dp[i] [j - 1], so the traversal order should also be from top to bottom and from left to right
-
Print dp array
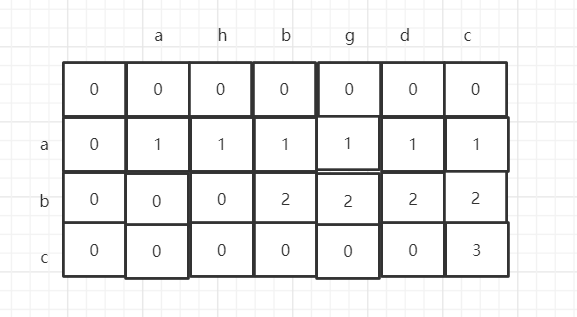
3. Code
class Solution {
public boolean isSubsequence(String s, String t) {
int[][] dp = new int[s.length() + 1][t.length() + 1];
for (int i = 1; i <= s.length(); i++) {
for (int j = 1; j <= t.length(); j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = dp[i][j - 1];
}
}
}
return dp[s.length()][t.length()] == s.length();
}
}
115. Different subsequences
1. Title
Given a string s and a string t, calculate the number of occurrences of T in the subsequence of S.
A subsequence of a string refers to a new string formed by deleting some (or no) characters without disturbing the relative position of the remaining characters. (for example, "ACE" is a subsequence of "ABCDE" and "AEC" is not)
The question data ensures that the answer conforms to the range of 32-bit signed integers.
Example 1:
Input: s = "rabbbit", t = "rabbit" Output: 3 Explanation: As shown in the figure below, There are three kinds of s Get in "rabbit" A new scheme. rabbbit rabbbit rabbbit
Example 2:
Input: s = "babgbag", t = "bag" Output: 5 Explanation: As shown in the figure below, There are 5 kinds of s Get in "bag" A new scheme. babgbag babgbag babgbag babgbag babgbag
Tips:
- 0 <= s.length, t.length <= 1000
- s and t consist of English letters
2. Ideas
This question is still a question of editing distance type. You only need to consider the deletion of string
-
Confirm the meaning of dp array and subscript, indicating the number of subsequences of t ending with j - 1 in the s subsequence ending with i - 1
-
When confirming the state transition equation, the following two cases should be considered
- if (s.charAt(i - 1) == s,charAt(j))
- if (s.charAt(i - 1) != s,charAt(j))
When s.charAt(i - 1) == s,charAt(j), dp[i][j] can be composed of two parts
- Part uses s.charAt[i - 1] to match the string t, and the number is dp[i - 1] [j - 1]
- The other part is the string t that does not match s.charAt[i - 1], and the number is dp[i - 1] [j]
Why consider not using s.charAt[i - 1]?
For example, s is "bag", t is "bag", which can be composed of ba and two g
-
It can be seen from the state transition equation that the initialization of the array depends on dp[i - 1] [j - 1] and dp[i - 1] [j]. As shown in the following figure, remember to remember the meaning of dp array
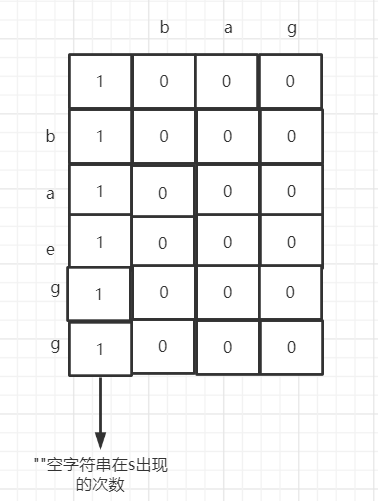
-
Traversal order, from top to bottom, from left to right
-
Print dp array
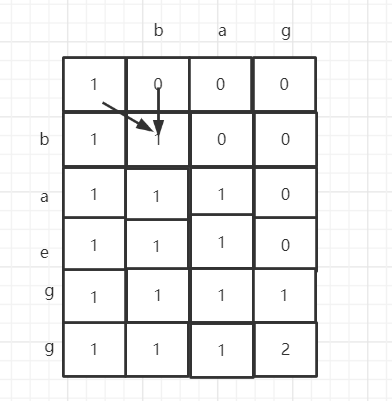
3. Code
class Solution {
public int numDistinct(String s, String t) {
//dp[i][j] represents the number of occurrences of s in the sequence of i-1 and t in the sequence of j-1
int[][] dp = new int[s.length() + 1][t.length() + 1];
//initialization
//Represents the number of empty strings t in s sequence
for (int i = 0; i <= s.length(); i++) {
dp[i][0] = 1;
}
//Indicates the number of t subsequences in an empty string
//for (int j = 1; j <= t.length(); j++) {
// dp[0][j] = 0;
//}
//Number of occurrences t of s subsequence
for (int i = 1; i <= s.length(); i++) {
for (int j = 1; j <= t.length(); j++) {
//If subsequences are equal
//The elements in s sequence are deleted, and the elements in t cannot be deleted, so it is dp[i - 1][j]
if (s.charAt(i - 1) == t.charAt(j - 1)) {
//If equal, there are two cases: 1 Using this letter, then dp[i - 1][j - 1] 2 If the last bit is not used, it is dp[i - 1][j], and the two can be added together
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
//If it is not equal, it means that the element does not need to be retained directly. You can delete the element and hope to remove the sequence of this element, that is, dp[i][j] = dp[i - 1][j]
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[s.length()][t.length()];
}
}
583. Deletion of two strings
1. Title
Given two words word1 and word2, returns the minimum number of steps required to make word1 and word2 the same.
One character in any string can be deleted in each step.
Example 1:
input: word1 = "sea", word2 = "eat" output: 2 explain: The first step will be "sea" Become "ea" ,The second step will be "eat "Become "ea" Example 2: Input: word1 = "leetcode", word2 = "etco" Output: 4
Tips:
- 1 <= word1.length, word2.length <= 500
- word1 and word2 contain only lowercase English letters
2. Ideas
The difference between this question and the previous two questions is that both strings can be operated
-
Determine the meaning of dp array (dp table) and subscript, dp[i][j]: the minimum number of times to delete elements in order to achieve equality between string word1 ending in i-1 and string word2 ending in j-1 bit.
-
Determine recurrence formula
- When word1[i - 1] is the same as word2[j - 1]
- When word1[i - 1] is different from word2[j - 1]
When word1[i - 1] is the same as word2[j - 1], dp[i] [j] = dp[i - 1] [j - 1];
When word1[i - 1] is different from word2[j - 1], there are three situations:
Case 1: delete word1[i - 1], and the minimum number of operations is dp[i - 1] [j] + 1
Case 2: delete word2[j - 1], and the minimum number of operations is dp[i] [j - 1] + 1
Case 3: delete word1[i - 1] and word2[j - 1] at the same time. The minimum number of operations is dp[i - 1] [j - 1] + 2. Finally, take the minimum value
-
Initialize dp array and remember the meaning of dp array

- It can be seen from the recursive formula that dp[i] [j] depends on dp[i - 1] [j - 1] and dp[i - 1] [j] and dp[i] [j - 1], so the traversal order is from top to bottom and from left to right

- Print dp array

3. Code
class Solution {
public int minDistance(String word1, String word2) {
int[][] dp = new int[word1.length() + 1][word2.length() + 1];
for (int i = 1; i <= word1.length(); i++) {
dp[i][0] = i;
}
for (int j = 1; j <= word2.length(); j++) {
dp[0][j] = j;
}
for (int i = 1; i <= word1.length(); i++) {
for (int j = 1; j <= word2.length(); j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
//The current element does not need to be deleted, but directly looks for the i - 1 and j - 1 sequences
dp[i][j] = dp[i - 1][j - 1];
} else {
//Delete word1 charAt(i - 1) + 1
//Delete word2 charAt(j - 1) + 1
//Two word1 charAt(i - 1),word2. Charat (J - 1) all delete + 2
dp[i][j] = Math.min(dp[i - 1][j - 1] + 2, Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1)) ;
}
}
}
return dp[word1.length()][word2.length()];
}
}
72. Edit distance
1. Title
Here are two words word1 and word2. Please return the minimum operand used to convert word1 to word2.
You can perform the following three operations on a word:
- Insert a character
- Delete a character
- Replace one character
Example 1:
Input: word1 = "horse", word2 = "ros" Output: 3 Explanation: horse -> rorse (take 'h' Replace with 'r') rorse -> rose (delete 'r') rose -> ros (delete 'e')
Example 2:
Input: word1 = "intention", word2 = "execution" Output: 5 Explanation: intention -> inention (delete 't') inention -> enention (take 'i' Replace with 'e') enention -> exention (take 'n' Replace with 'x') exention -> exection (take 'n' Replace with 'c') exection -> execution (insert 'u')
Tips:
- 0 <= word1.length, word2.length <= 500
- word1 and word2 are composed of lowercase English letters
2. Ideas
This problem needs to pay attention to initialization and the meaning of dp array
Let's focus on the state transition equation
if (word1[i - 1] == word2[j - 1]), then dp[i][j] should be dp[i - 1] [j - 1] without any editing, that is, dp[i][j] = dp[i - 1] [j - 1]
In the whole process of dynamic gauge, the key is to correctly understand the definition of dp[i][j]!
If (word1 [I - 1]! = word2 [J - 1]), you need to edit it now. How to edit it?
- Operation 1: word1 deletes an element, then it is the nearest editing distance between word1 ending with i - 2 and word2 ending with j-1 plus an operation.
dp[i][j] = dp[i - 1][j] + 1;
- Operation 2: delete an element in word2, then it is the nearest editing distance between word1 ending with i - 1 and word2 ending with j-2, plus an operation.
Namely DP [i] [J] = DP [i] [J - 1] + 1; Adding an element in word2 is equivalent to deleting an element in word1. For example, word1 = "ad", word2 = "a", deleting element'd 'in word1 and adding an element'd' in word2 become word1="a", word2="ad", and the final operand is the same!
Operation 3: replace the element. Word1 replaces word1[i - 1] to make it the same as word2[j - 1]. At this time, there is no need to add elements. Then the nearest editing distance between word1 ending with i-2 and word2 ending with j-2 plus a replacement element.
Namely dp[i][j] = dp[i - 1][j - 1] + 1;
3. Code
class Solution {
//There are three operations involved in subsequence: insert, delete and replace
public int minDistance(String word1, String word2) {
int[][] dp = new int[word1.length() + 1][word2.length() + 1];
for (int i = 1; i <= word1.length(); i++) {
dp[i][0] = i;
}
for (int j = 1; j <= word2.length(); j++) {
dp[0][j] = j;
}
//The title requires that word1 be converted to word2
for (int i = 1; i <= word1.length(); i++) {
for (int j = 1; j <= word2.length(); j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
//How to insert a character? I just think of addition In fact, the subtraction of another character is the addition of this character
dp[i][j] = Math.min(dp[i][j - 1], Math.min(dp[i - 1][j], dp[i - 1][j - 1])) + 1;
}
}
}
return dp[word1.length()][word2.length()];
}
}
