1. Tree structure
1.1 concept (understanding)
The tree is no longer a one-to-one linear structure such as sequential list, linked list, stack and queue. The tree is a one to many data structure, which consists of n (n > = 0) disjoint finite node groups and hierarchical sets
The features are as follows:
- There is a special node, called the root node, which has no precursor node
- Except for the root node, the other nodes are divided into m (M > 0) disjoint sets T1, T2,..., Tm, where each set < = m) is a subtree similar to the tree. The root node of each subtree has only one precursor, and can have 0 or more successors
- The tree is recursively defined [the concept of tree is used in the definition of tree]
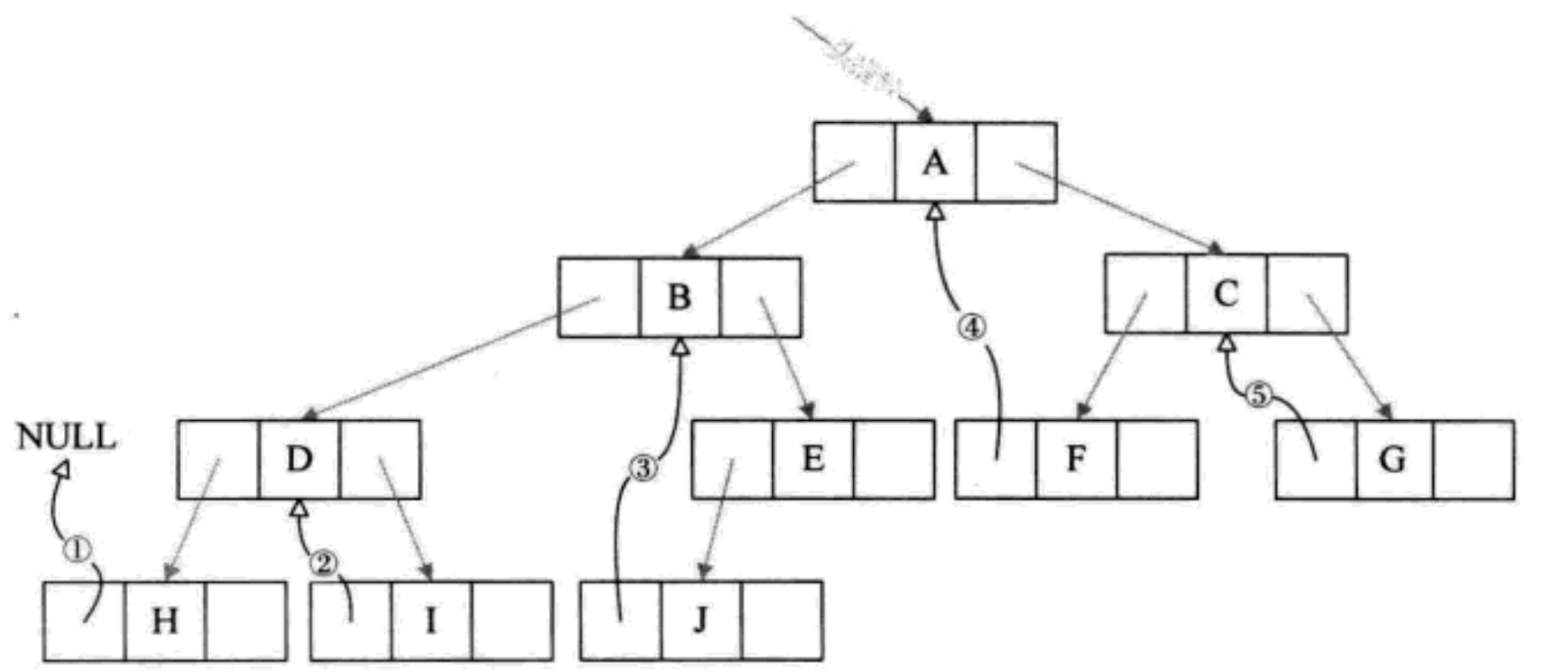
Correct tree:
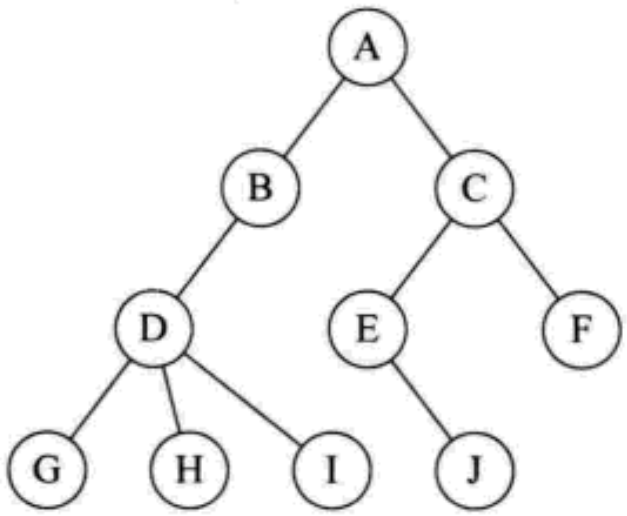
1.2 concept (important)
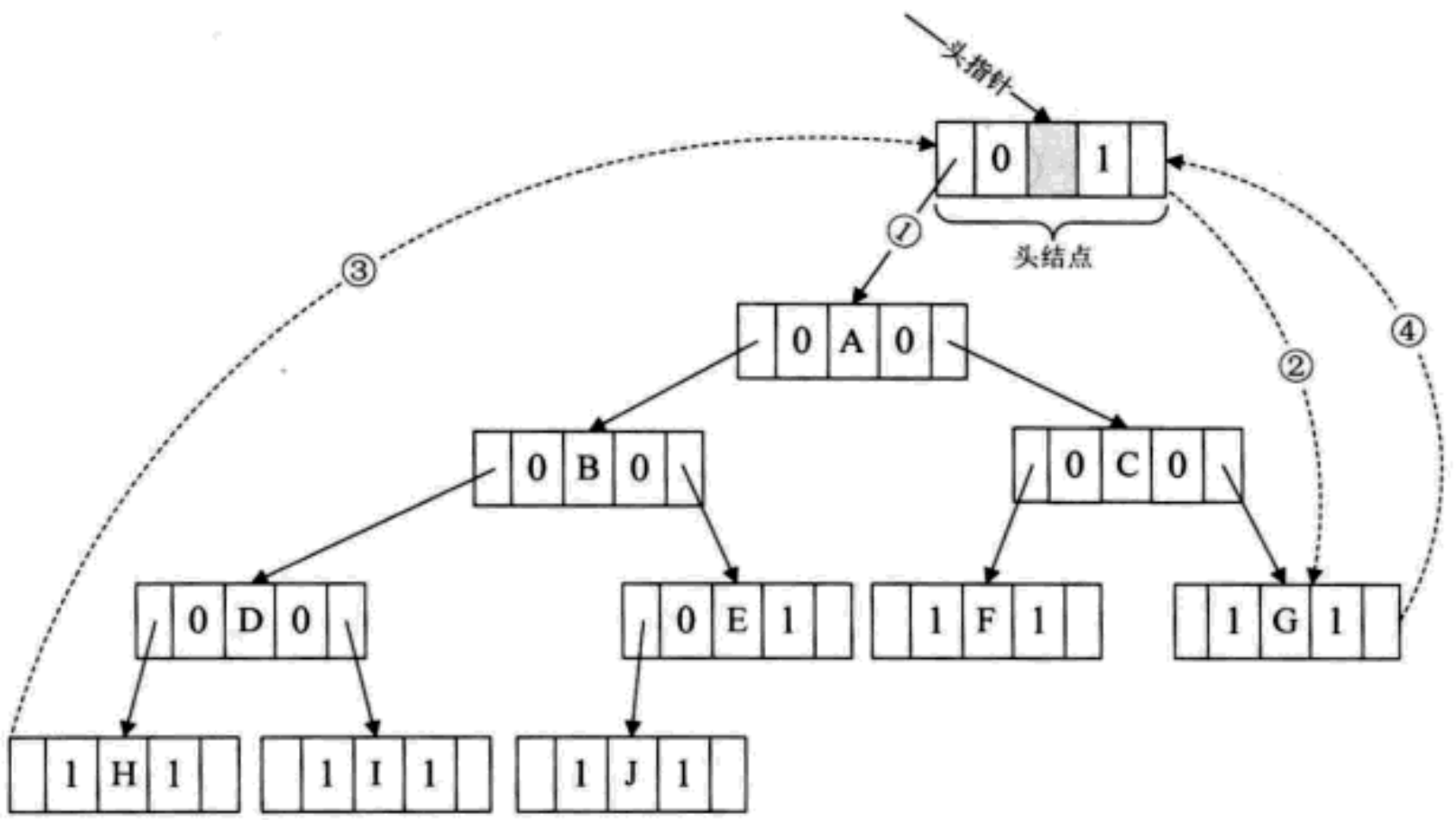
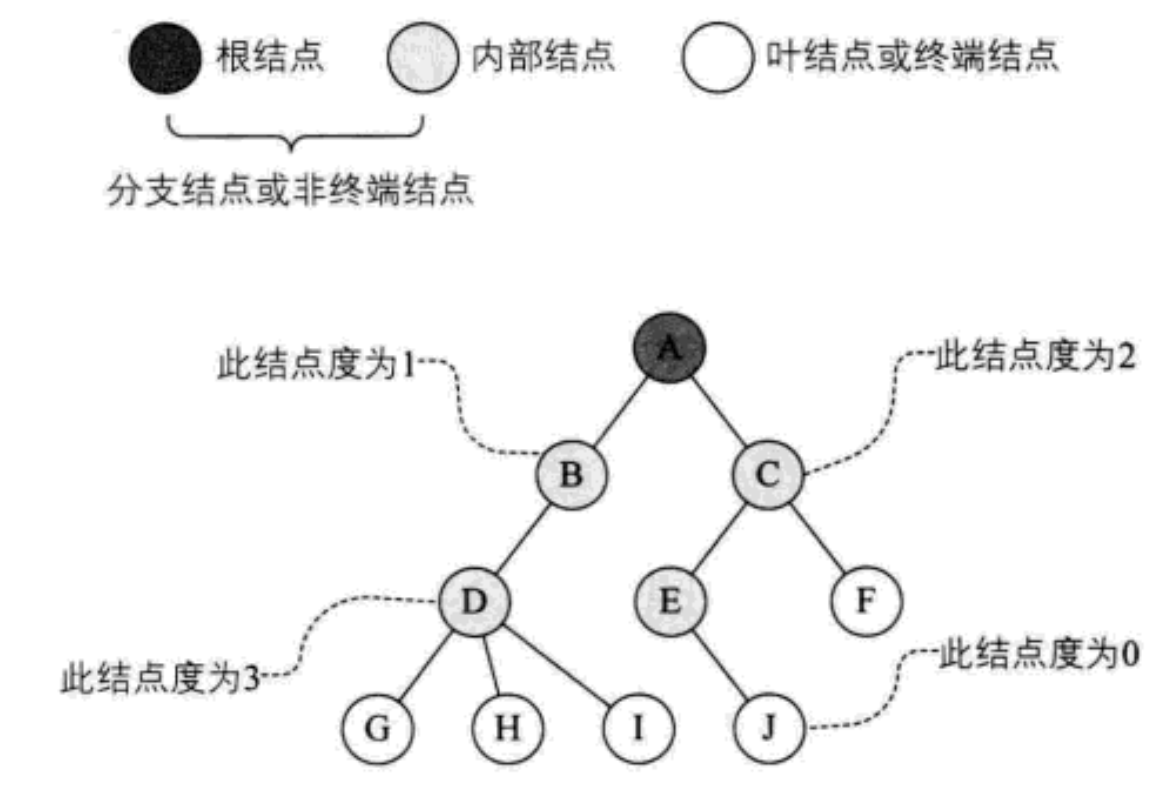
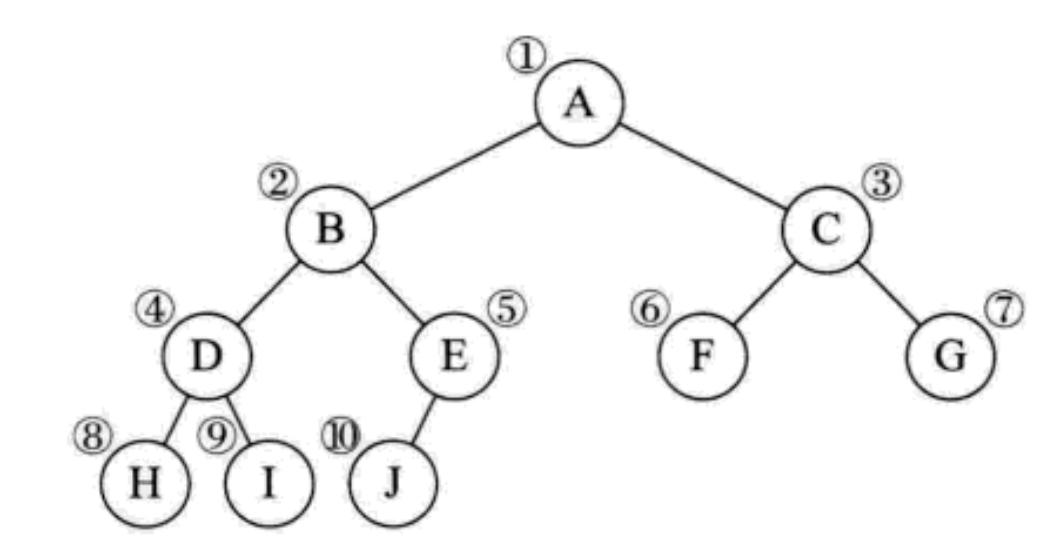
The correct binary tree in the figure above is used to explain the concept
-
Degree of node: the number of subtrees contained in A node is called the degree of the node [the degree of A is 2]
-
Non terminal node or branch node: node with degree not 0 [A, B, C, D, E]
-
Tree degree: the degree of the largest node in a tree is called the degree of the tree; As shown in the figure above: the degree of the tree is 3
-
Leaf node or terminal node: a node with a degree of 0 is called a leaf node; As shown in the figure above, nodes G, H, I and J are leaf nodes
-
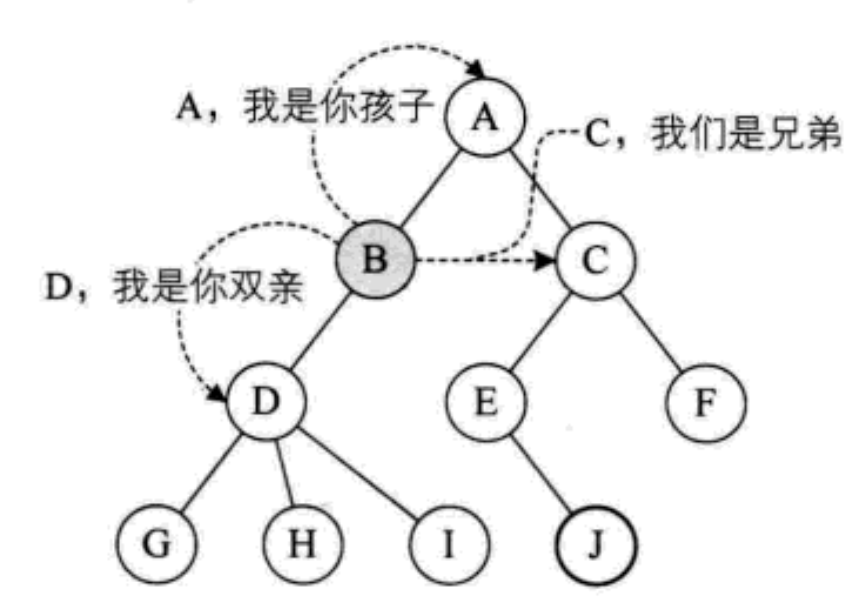
Parent node or parent node: if A node contains child nodes, this node is called the parent node of its child nodes; As shown in the figure above, A is the parent node of B
-
Child node or child node: the root node of the subtree contained in a node is called the child node of the node; As shown in the figure above: B is the child node of A
-
Sibling node: nodes with the same parent node are called sibling nodes [B and C, E and F, G, H and I]
-
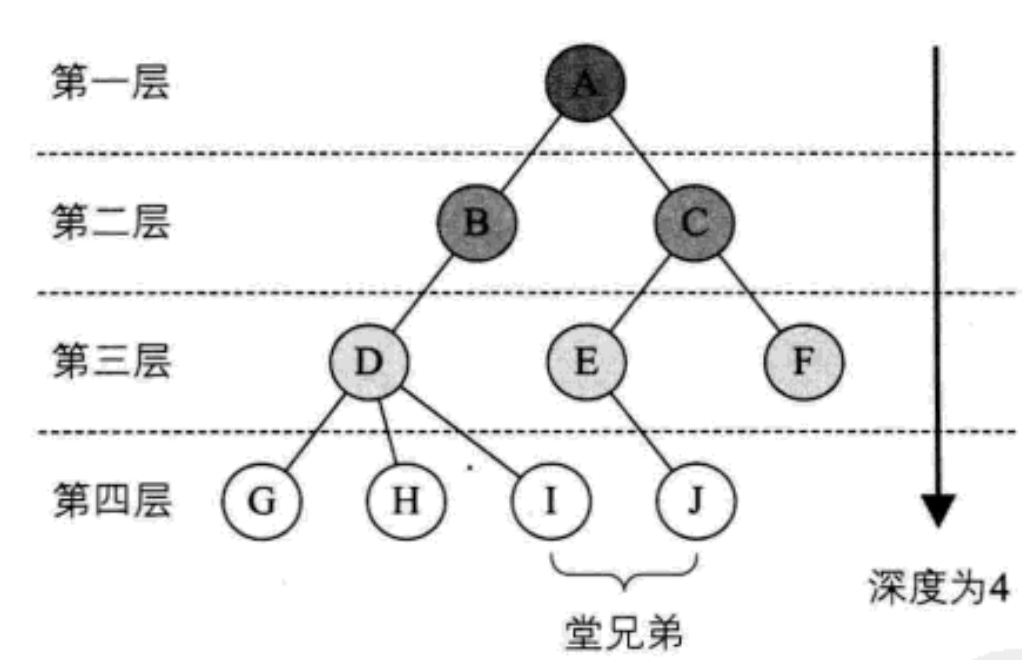
Cousin node: nodes with parents on the same layer are called cousin nodes [D and E, D and F]
-
Ancestor of node: all branches from the root to the node experience all nodes [A]
-
Root node: A node in A tree without parent nodes; As shown in the figure above: A
-
Forest: a collection of M (M > = 0) disjoint trees is called forest
-
Node hierarchy: defined from the root, the root is the first layer, and the child nodes of the root are the second layer, and so on
-
Height or depth of tree: the maximum level of nodes in the tree; As shown in the figure above: the height of the tree is 4
| linear structure | Tree structure |
|---|---|
| First element: no precursor | Root node: no parents |
| Last element: no successor | Leaf node: no successor, multiple nodes are allowed |
| Intermediate element: a precursor and a successor | Intermediate node: one parent, multiple children |
1.3 representation of tree
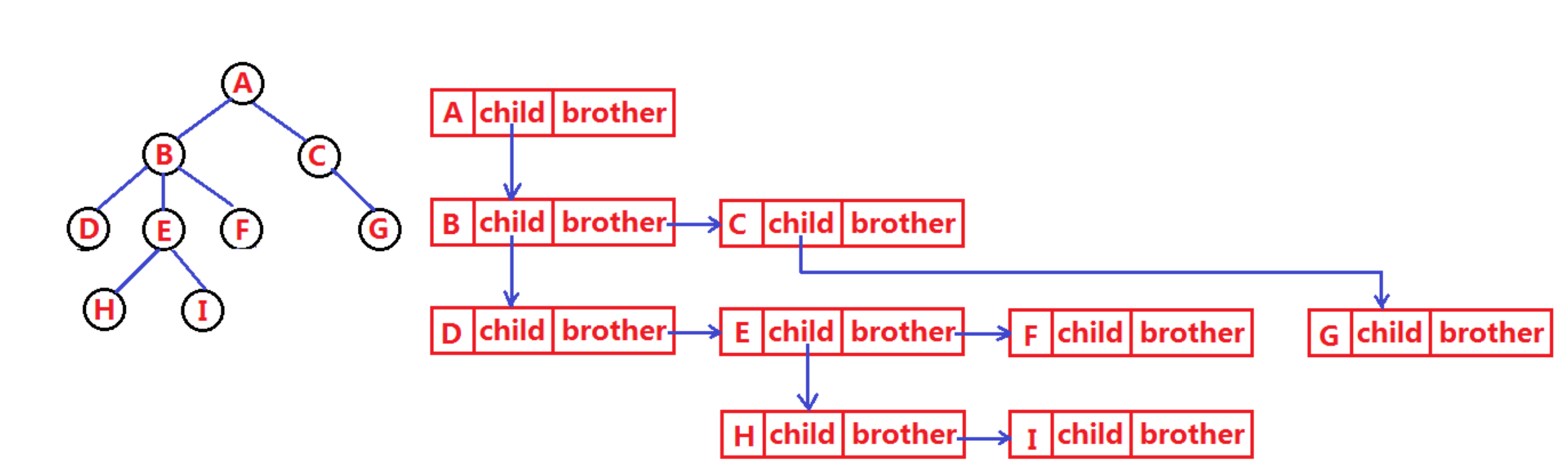
The tree structure is more complex than the linear table, and it is more troublesome to store and express. In fact, there are many kinds of tree representations, such as parent representation, child representation, child brother representation and so on. Let's simply understand the most commonly used expression of children's brothers here [this expression is often tested by online OJ]
class Node {
int value;// Data stored in the tree
Node child;// First child quote
Node brother;// Next brother reference
}
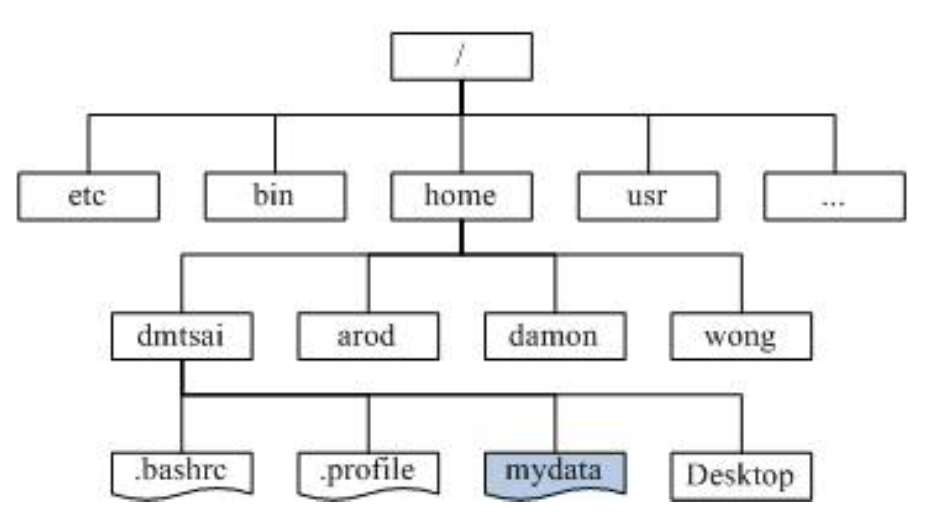
1.4 application of tree
File system management (directories and files)
2. Binary tree (BinaryTree focus)
2.1 concept
Let's start with the classic number guessing game and introduce the binary tree from simple to deep
How many times can you guess the number correctly within 100? The answer is: 7
The following is to build a binary tree according to the size of each guess


We find that using this size relationship to find a number in the specified range is not very efficient. Therefore, for this case with opposite relationship: 0 and 1, true and false, up and down, positive and negative, right and wrong, it is suitable to use tree modeling. This special tree structure is called binary tree
A binary tree is a finite set of nodes. The set is either empty or composed of a root node and two binary trees called left subtree and right subtree.
characteristic:
- Each node can have at most 2 subtrees, that is, there are no nodes with a degree greater than 2
- A binary tree can be divided into left and right subtrees, and the order cannot be reversed. Therefore, a binary tree is also an ordered tree
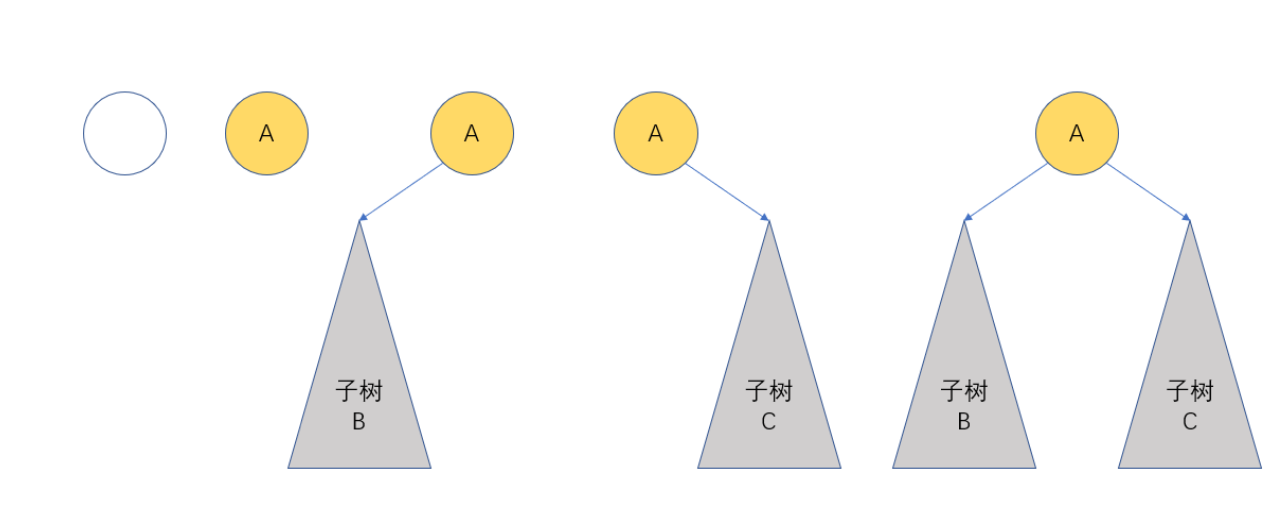
2.2 five basic forms of binary tree
- Empty binary tree
- There is only one root node
- The root node has only the left subtree
- The root node has only the right subtree
- The root node has both left and right subtrees
2.3 two special binary trees
2.3.1 oblique tree
As the name suggests, a skew tree must be skew, and there is a stress on where to skew. All nodes have only a left subtree, which is called a left skew tree; All nodes have only right subtree, which is called right skew tree
Left oblique tree:

Right oblique tree:
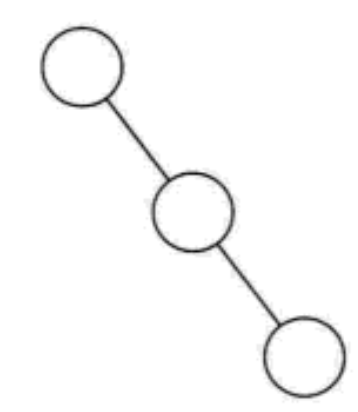
Skew tree has obvious characteristics: each layer has only one node, and the number of nodes is the same as the depth of the tree
Some students are surprised: can this also be called a tree? Isn't this a familiar linear table?
Explanation: Yes, linear table structure can be understood as an extremely special form of tree
2.3.2 full binary tree
In a binary tree, if all branch nodes have left and right subtrees, and all leaf nodes are on the same layer, such a binary tree is called full binary tree
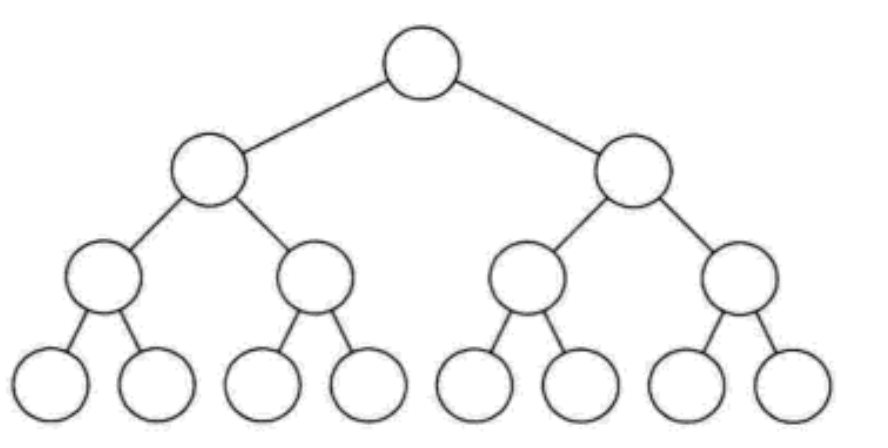
It looks beautiful and symmetrical
Full binary tree features:
- Leaf nodes can only appear in the lowest layer, and it is impossible to achieve balance if they appear in other layers
- The degree of non leaf node must be 2. No thief is "lack of arms and legs"
- In the same depth binary tree, the full binary tree has the most nodes and the leaf nodes
2.3.3 complete binary tree
A binary tree with n nodes is numbered according to sequence. The node numbered i (< 1 = i < = n) is exactly the same as the node numbered i in the full binary tree with the same depth
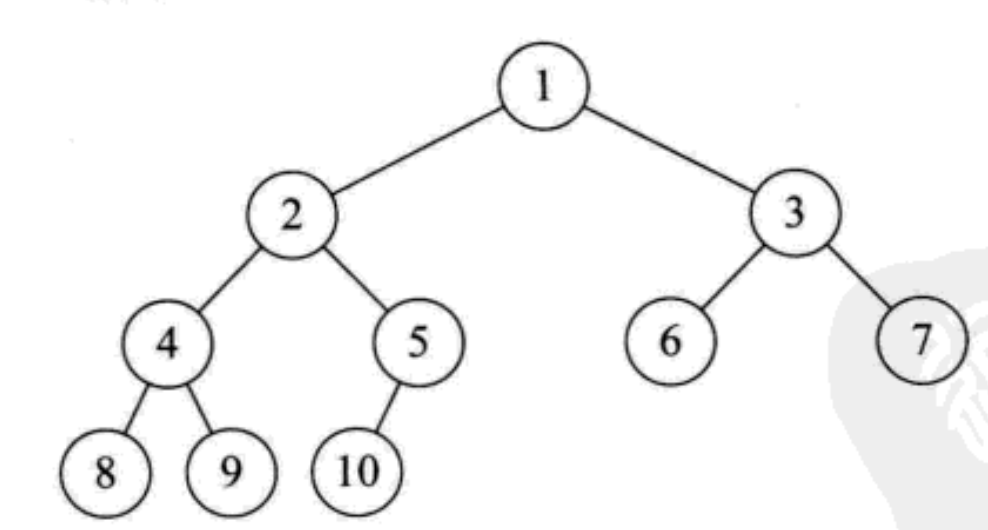
This is a kind of special binary tree which is difficult to understand
First, the difference between "full" and "complete" is understood and distinguished literally: a full binary tree must be a complete binary tree, but a complete binary tree is not necessarily a full binary tree
What is sequence numbering?
In the above figure, the sequence number of 1, 2, 3,..., n is from top to bottom and from left to right
Complete binary tree features:
- Leaf nodes can only appear in the bottom two layers
- The lowest leaf nodes must be concentrated in the left continuous position
- If there are leaf nodes on the penultimate layer, they must be in the continuous position on the right
- If the degree of a node is 1, the node has only left children, that is, there is no case of only right subtree
- For a binary tree with the same number of nodes, the depth of a complete binary tree is the smallest
From the above columns, we are also given a way to judge whether a binary tree is a complete binary tree: look at the schematic diagram of the binary tree and silently number each node layer by layer according to the structure of the full binary tree. If there is a gap in the number, it means that it is not a complete binary tree, otherwise it is a complete binary tree
2.4 properties of binary tree
2.4.1 number of nodes in layer i
If the number of layers of the specified root node is 1, there are at most 2 ^ (i-1) (I > 0) nodes on layer I of a non empty binary tree
2.4.2 maximum number of all points in the tree
If the number of layers of the root node is specified as 1, the maximum number of nodes of the binary tree with depth K is 2 ^ k-1 (k > 0)
2.4.3 quantitative relationship between leaf nodes and non leaf nodes
For any binary tree, if the number of leaf nodes is n0 and the number of non leaf nodes with degree 2 is n2, then n0=n2+1 [the number of leaf nodes in the lowest layer = the number of all non leaf nodes above + 1]
2.4.4 calculating tree depth according to nodes
The depth K of a binary tree with n nodes is log2^(n+1) rounded up
2.4.5 numbering relationship between parent and child nodes
For a complete binary tree with n nodes, if all nodes are numbered from 0 from top to bottom and from left to right, the nodes with sequence number i are:
- If I > 0, parental serial number: (i-1)/2;
- If i=0, i is the root node number and there is no parent node
- If 2i+1 < n, left child serial number: 2i+1, otherwise there is no left child
- If 2i+2 < n, right child serial number: 2i+2, otherwise there is no right child
This rule is very important, involving heap and row. This rule is needed for binary search trees
2.4.6 small training
If there are 1000 nodes in a complete binary tree, there are 500 leaf nodes, 500 non leaf nodes, 1 node has only left children and 0 has only right children
Calculation steps of 500 leaf nodes
- Total number of leaf nodes = number of leaf nodes on layer 10 + number of leaf nodes on layer 9
Some students will think: Why are there leaf nodes on the 9th floor?
Explanation: we found that there are 1000 nodes in this tree and 2 ^ 10-1 nodes in a full binary tree, so it means that layer 10 is not full and layer 9 must have leaf nodes
With this understanding, we can make further calculations
- Layer 10 is the number of leaf nodes: the number of summary points of the tree - the number of all nodes on layer 9 and above
Because it is a complete binary tree, it can be guaranteed that the ninth layer must be a full binary tree
Formula: 1000 - (2 ^ 9-1) – > 1000-511 = 489
Now we are still short of the number of leaf nodes on the 9th floor
- Number of leaf nodes in layer 9: number of nodes in layer 9 - number of parent nodes in layer 10
Formula: 2 ^ (9-1) - number of parent nodes in layer 10
The final problem is to find the number of layer 10 parent nodes
- Calculation of the number of parent nodes in layer 10
If the number of nodes n is even, the number of parent nodes is n/2
If the number of nodes n is odd, the number of parent nodes n/2+1
In the first step, we get the number of parent nodes of layer 10. The number of parent nodes of layer 10 is: 489 / 2 + 1 – > 245 - Now you can calculate the number of leaf nodes on layer 9 in step 3:
2^(9-1)-245–>256-245=11 - Now you can calculate the leaf nodes of all the whole trees in step 1;
Number of nodes on the 10th layer + number of nodes on the 9th leaf: 489 + 11 = 500 - With the number of leaf nodes, it is easy to know non leaf nodes
Number of summary points - number of leaf nodes: 1000-500 - Since the number of nodes in the 10th layer of a complete binary tree is 489, which is an odd number, there must be 1 node with only left children and 0 nodes with only right subtrees
Start a complete binary tree with 100 nodes from the root layer, and number the nodes in each layer from left to right. If the root node number is 1, the parent node number of the node numbered 98 is: (98-1) / 2 = 48
In all subtrees of a non empty binary tree, if the node values on the left subtree are less than the root node values, and the node values on the right subtree are not less than the root node values, the binary tree is called a sorted binary tree. The traversal result of the sorted binary tree is an ordered sequence: medium order traversal
Put the root node of a binary tree into the queue, and then recursively perform the following operations to join all child nodes of the out of queue node into the queue. The above operations can realize sequence traversal
How many layers can a complete binary tree with n nodes have at most: rounding on log(n+1)
2.5 storage of binary tree
2.5.1 sequential storage
The sequential storage of binary tree uses a one-dimensional array to store the nodes in the binary tree, and the storage location should reflect the logical relationship between nodes, such as children's parents, left and right brother nodes
2.5.1.1 complete binary tree storage
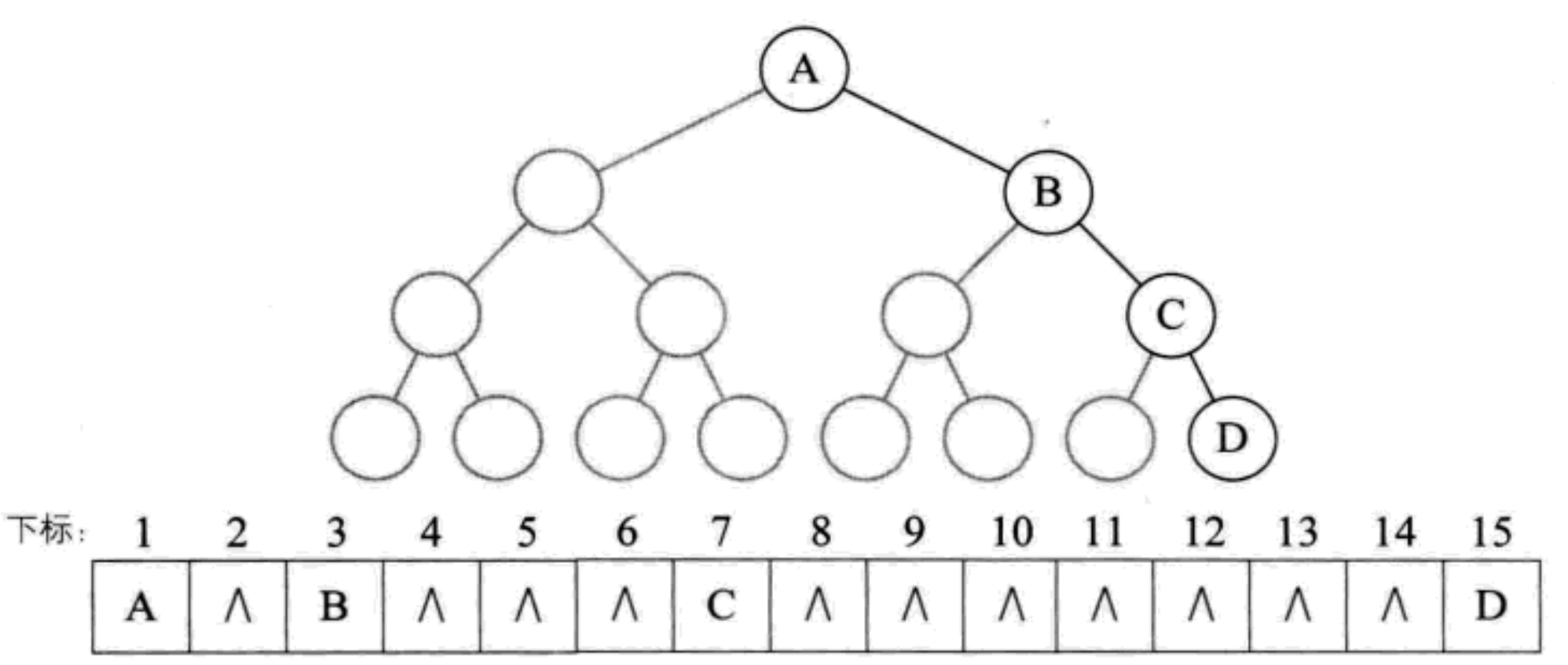
Store the binary tree in the array, and the corresponding subscripts correspond to their equal positions

This shows the advantages of a complete binary tree. Because it is strictly defined, the sequential structure can also show the structure of a binary tree
2.5.1.2 general tree storage
For a general binary tree, the sequence number cannot reflect the logical relationship, but it can be numbered according to the complete binary tree, except that the nonexistent node facilities are '^'. Light colored nodes represent nonexistence

Consider the extreme case: another oblique tree [left oblique tree]
A right skew tree with depth K has only K nodes, but needs to allocate 2^k-1 storage units, which is obviously a waste of storage space. Therefore, sequential storage is only applicable to complete binary trees
2.5.2 chain storage
Since the adaptability of sequential storage is not strong, we should consider the chain storage structure. Each node of binary tree has at most two children, so it is ideal to design one data field and two pointer fields. This is binary linked list
Child representation

class Node {
int val;// Data domain
Node left;// The reference of the left child often represents the whole left subtree with the left child as the root
Node right;// The reference of the right child often represents the whole right subtree with the right child as the root
}

The child parent representation is mainly used in the balanced tree. This paper uses the child representation to construct the binary tree. Most online OJ topics also use this method to construct the binary tree
3. Binary tree analysis from simple to deep
3.1 traversing binary tree
3.1.1 traversal principle of binary tree
Introduction: suppose 20 100 yuan and 2000 1 yuan lotteries are thrown into the air at the same time. Let's compete to see who is the most in the middle
I believe students will say: pick up 100 yuan first. The reason is very simple, because picking up 100 yuan is equal to picking up 100 1 yuan. The efficiency is not a little good 🤏.
So we come to the conclusion that order is very important to achieve the highest efficiency in a limited time. For the traversal of binary tree, order is also very important
Traversing binary tree: starting from the root node, access all nodes in the binary tree in a certain order, so that each node is accessed once and only once
There are two key words here: sequential and access. Different from linear structure, it is at most simple traversal methods such as from beginning to end, circulation and two-way. There is no unique precursor and successor relationship between tree nodes. After visiting a node, the next visited node faces different choices. Just like which city you will face on the road of your life, Which university, specific major, etc. the order of traversal is completely different with different selection methods
3.1.2 binary tree traversal method
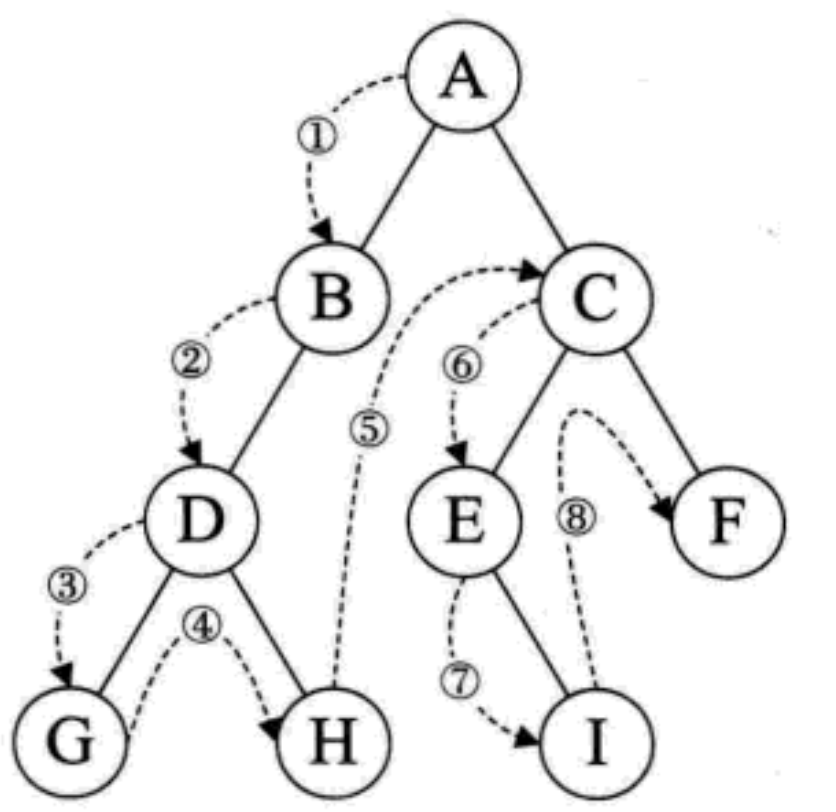
3.1.2.1 preorder traversal
- If the binary tree is empty, the empty operation is returned
- Otherwise, the root node is accessed first, and then the left subtree is traversed first, and then the right subtree is traversed first
- The result of the final visit is ABDGHCEIF
As shown in the figure below, the root accesses the binary tree in the left and right order
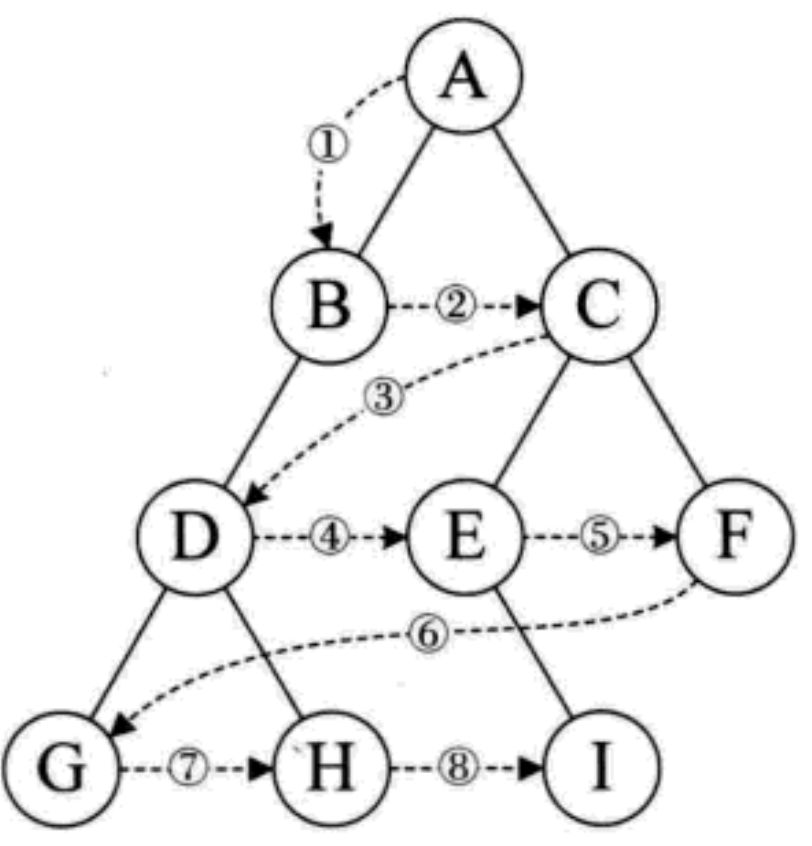
3.1.2.2 middle order traversal
- If the tree is empty, an empty operation is returned
- Otherwise, start from the root node (note that the root node is not accessed first)
- Traversing the left subtree of the root node in middle order
- Then access the root node
- Finally, traverse the right subtree in middle order
- The final access result is GDHBAEICF
As shown in the figure below, the binary tree is accessed in the order of left root and right

3.1.2.3 post order traversal
- If the tree is empty, an empty operation is returned
- No, first traverse and access the left and right subtrees from the left to the right line leaf node and then the node, and finally access the root node
- The final access result is GHDBIEFCA
As shown in the figure below, the left and right roots access the binary tree in order

3.1.2.4 sequence traversal
- If the tree is empty, an empty operation is returned
- Otherwise, access starts from the first layer of the tree, the root node
- Traverse layer by layer from top to bottom
- In the same layer, the nodes are accessed one by one from left to right
- The final access result is ABCDEFGHI
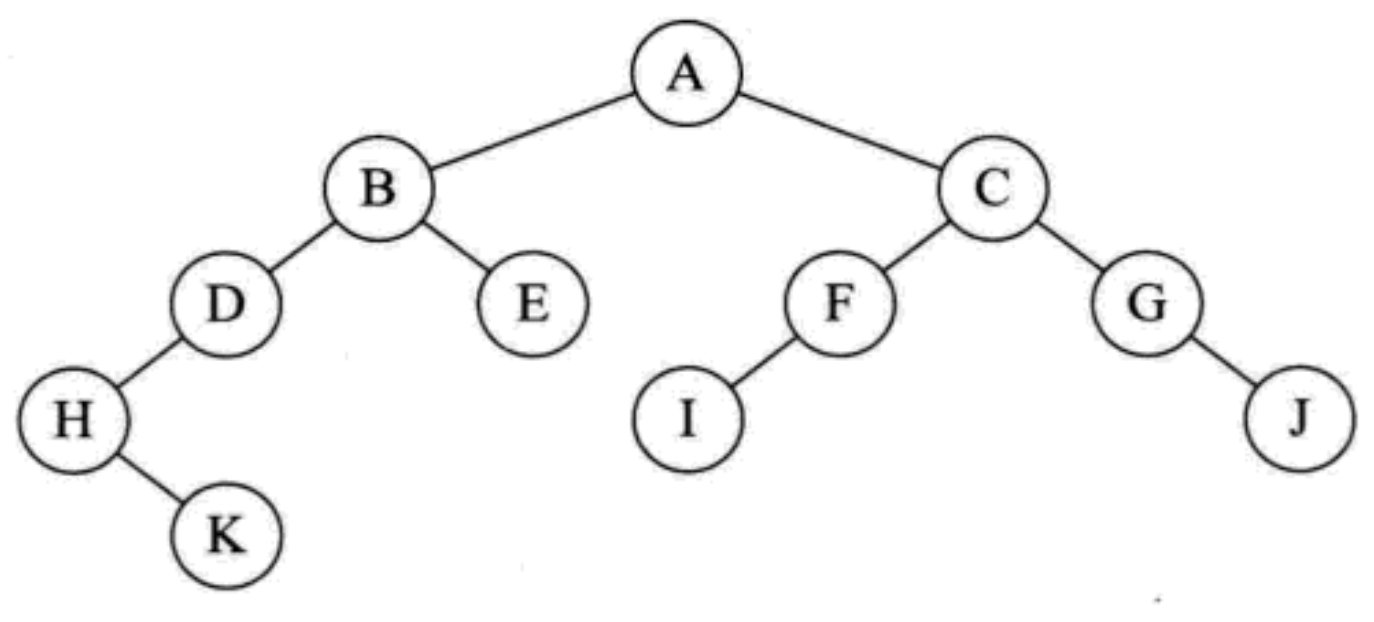
3.1.3 binary tree traversal algorithm
Suppose we have the following binary tree T, which is stored in a linked list structure
3.1.3.1 preorder traversal algorithm root
OJ topic link
Recursive preorder traversal
private static void preOrderTraversal(BinaryTreeNode root) {
if (root == null) {
return;
} else {
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}
}
private static List<String> preOrderTraversal(BinaryTreeNode root) {
List<String> result = new ArrayList<>();
if (root == null) {
return result;
} else {
result.add(root.val);
result.addAll(preOrderTraversal(root.left));
result.addAll(preOrderTraversal(root.right));
return result;
}
}
A B D H K E C F I G J
Demonstrate recursive preorder traversal steps
- Call preordertraversal (BinaryTreeNode root), the root node is not empty, so execute System.out.print(root.val + ""); Print letter A
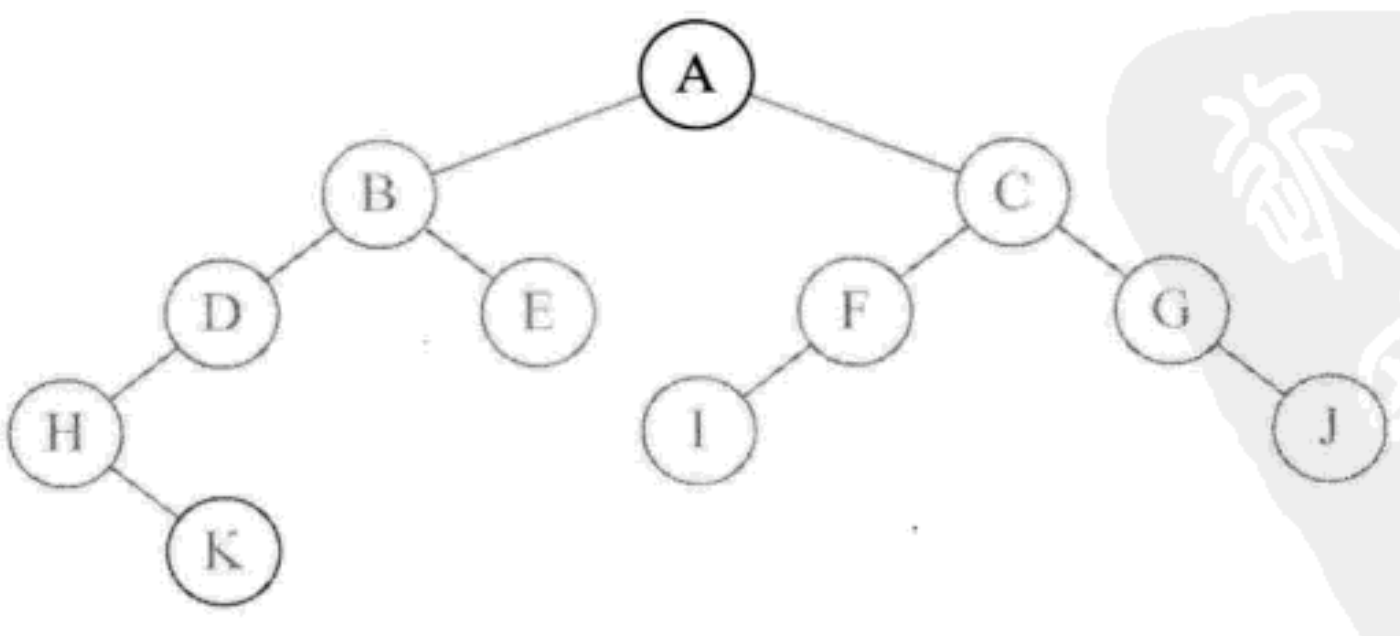
- Call preOrderTraversal(root.left), access the left child of node A, which is not null, and execute System.out.print(root.val + ""); Print letter B

- Call preOrderTraversal(root.left) recursively again, access the left child of node B, and execute System.out.print(root.val + ""); Print letter D

- Call preOrderTraversal(root.left) recursively again, access the left child of node D, and execute System.out.print(root.val + ""); Print letter H
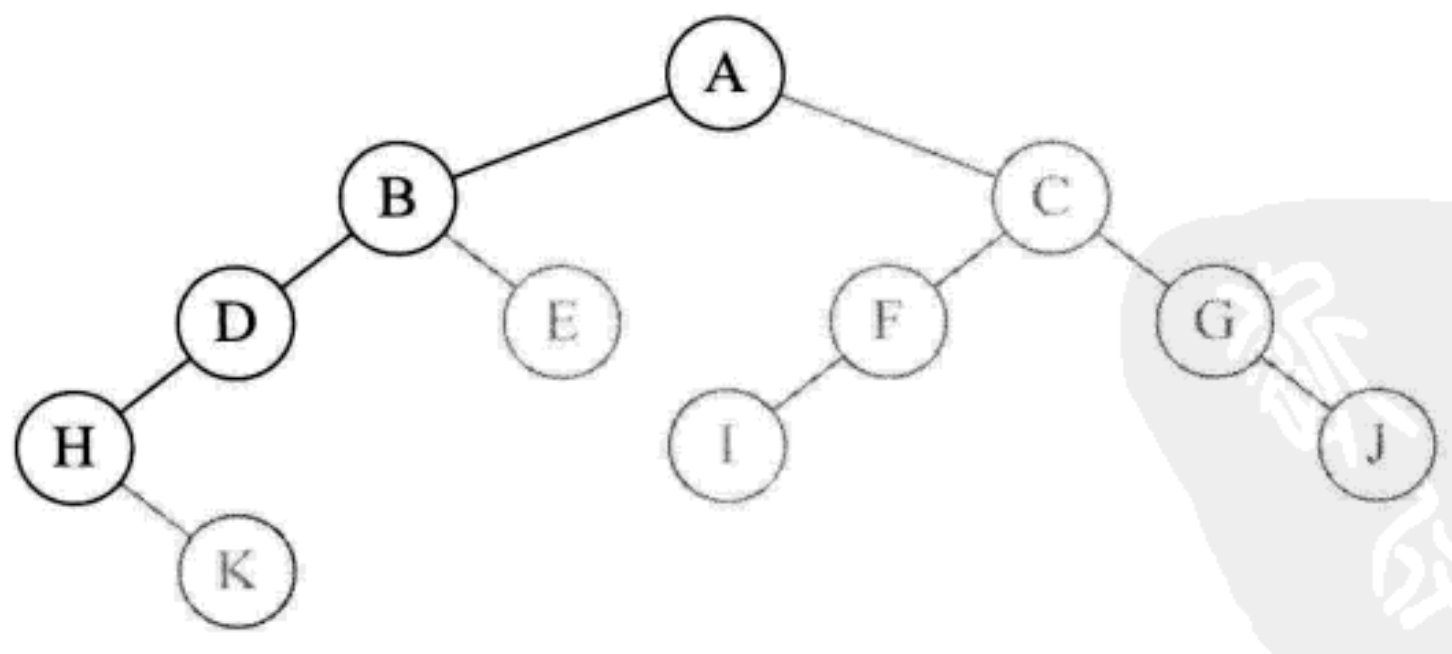
- Call preOrderTraversal(root.left) recursively again to access the left child of node H. at this time, because node H has no left child, root == null returns this function. At this time, call preOrderTraversal(root.right) recursively; Access the right child of node H and execute System.out.print(root.val + ""); Print letter K

- Call preOrderTraversal(root.left) recursively again to access the left child of node K and return
Call preOrderTraversal(root.right), access the right child of node K, which is also null, and return. Then the function is completed
The recursive function returned to the upper level (that is, the function when printing the H node) is also executed. [the left and right roots have been traversed, so the execution is completed]
Return the function when printing the D node. Call preordertraversal (root. Right) to access the right child of the D node. It does not exist
Return to node B, call preOrderTraversal(root.right), access the right child of node B, and print the letter E
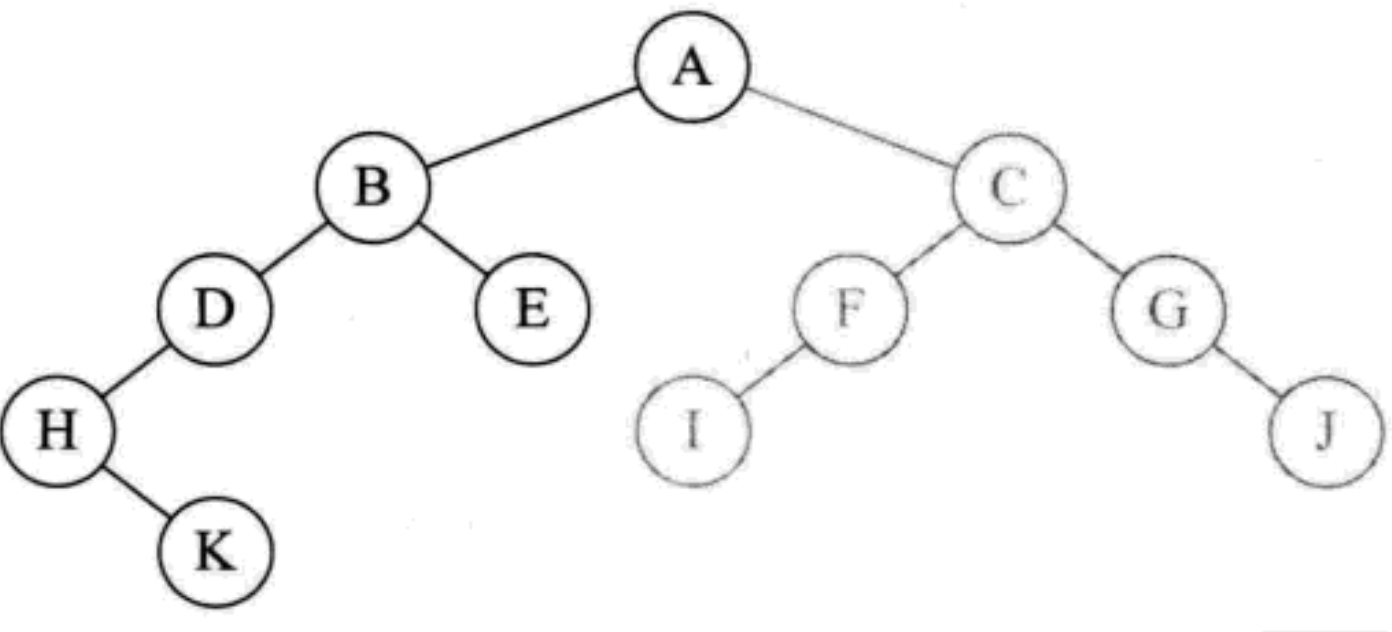
- Since node E has no left and right children, return the recursive function when printing node B, and the recursive execution is completed. Return to the original preOrderTraversal(root), call preOrderTraversal(root.right), access the right child of node A, and print the letter C
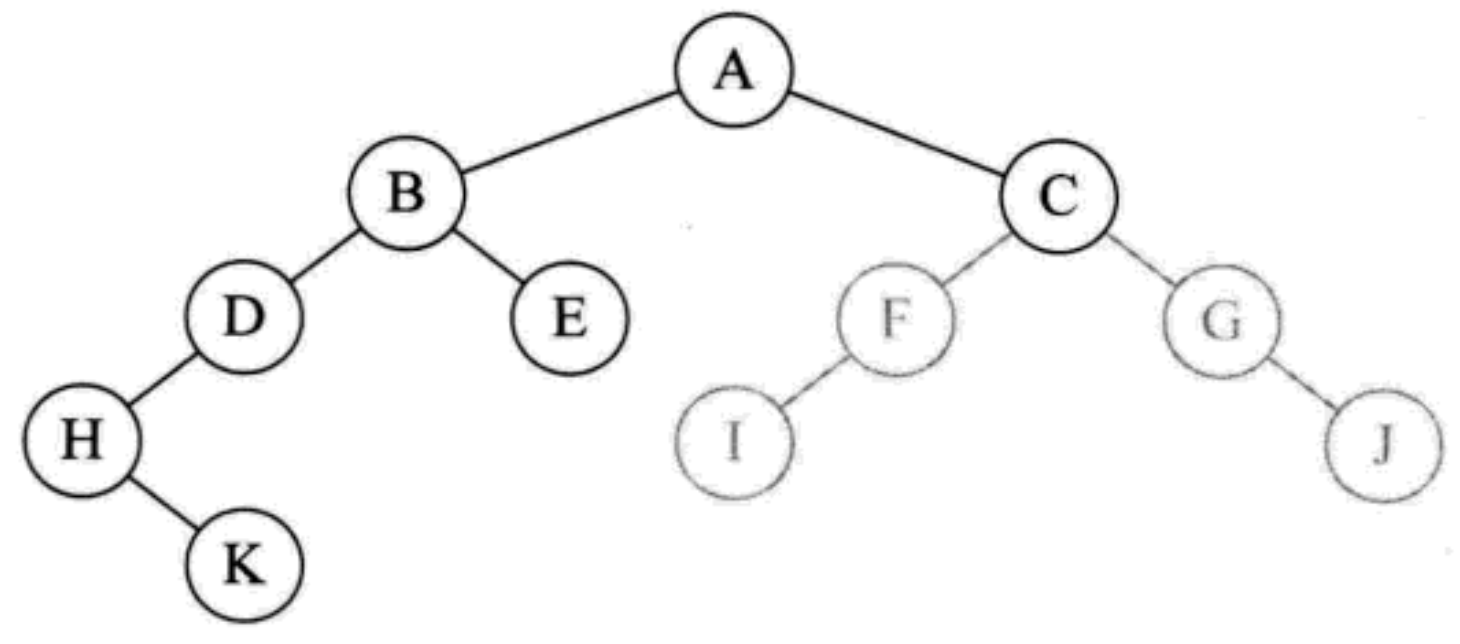
- After that, similar to the previous recursive call, continue to print F, I, G and j at one time
Knowing how recursive code works, let's take a look at non recursive preorder traversal
/*
non-recursive
1.Create a stack first
2.Put the root node on the stack
3.Loop stack top element
4.Get out of the stack and access the element value field
5.Put the right subtree of the current element into the stack, and then the left subtree into the stack [because the left subtree is printed first and then the right subtree is printed, for the stack, the right subtree should be entered first and then the left subtree]
*/
private static void preOrderTraversalNo(BinaryTreeNode root) {
if (root == null) {
return;
} else {
Stack<BinaryTreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.empty()) {
BinaryTreeNode top = stack.pop();
System.out.print(top.val + " ");
if (top.right != null) {
stack.push(top.right);
}
if (top.left != null) {
stack.push(top.left);
}
}
}
}
A B D H K E C F I G J
Demonstrate the pre iteration traversal steps

The non recursive idea makes ingenious use of the first in and last out characteristics of the stack for pre order traversal
3.1.3.2 middle order traversal algorithm left root right
OJ topic link
Recursive middle order traversal
private static void inOrderTraversal(BinaryTreeNode root) {
if (root == null) {
return;
} else {
preOrder(root.left);
System.out.print(root.val + " ");
preOrder(root.right);
}
}
H K D B E A I F C G J
Demonstrate sequence traversal steps in recursion
- Call inordertraversal (BinaryTreeNode root), the root node A of root is not null, so call inOrderTraversal(root.left) to access node B; If B is not empty, continue to call inOrderTraversal(root.left) to access node D; If D is not empty, continue to call inOrderTraversal(root.left) to access node h; If h is not empty, continue to call inOrderTraversal(root.left) to access the left child of node h; If it is empty, return. Print the current node H
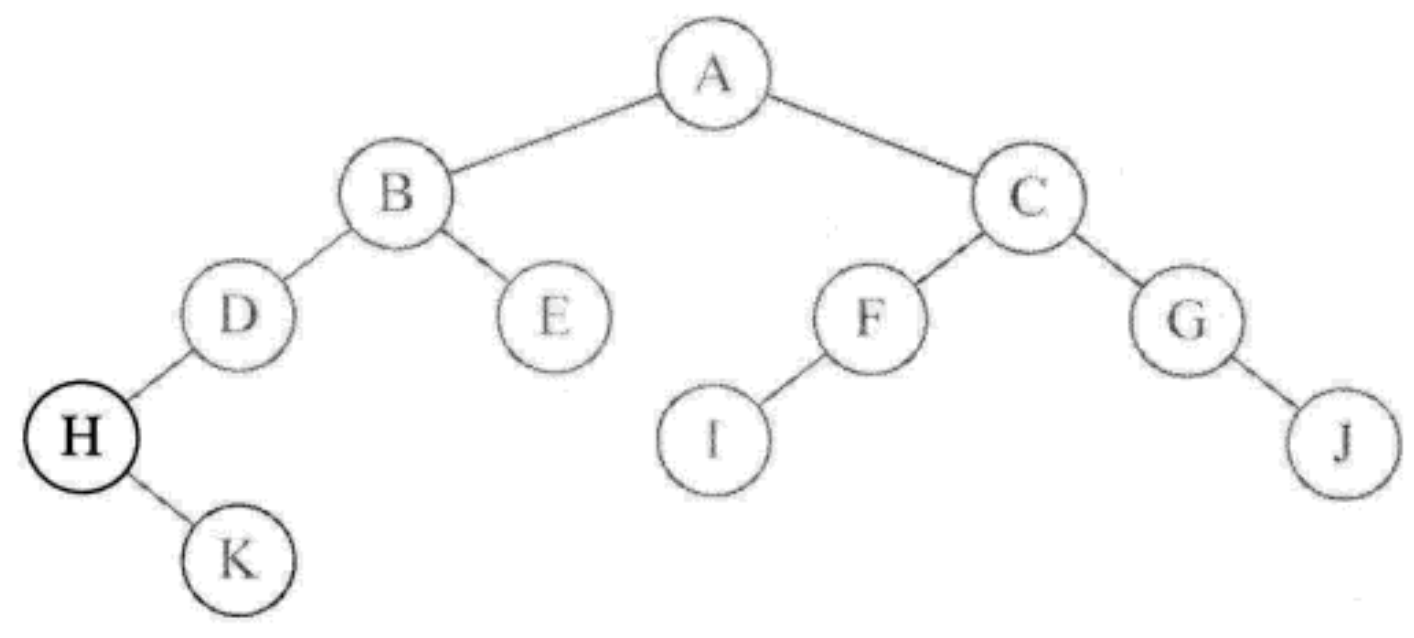
- Then call inOrderTraversal(root.right) to access the H node's right node K. because K does not have left child, so print K.
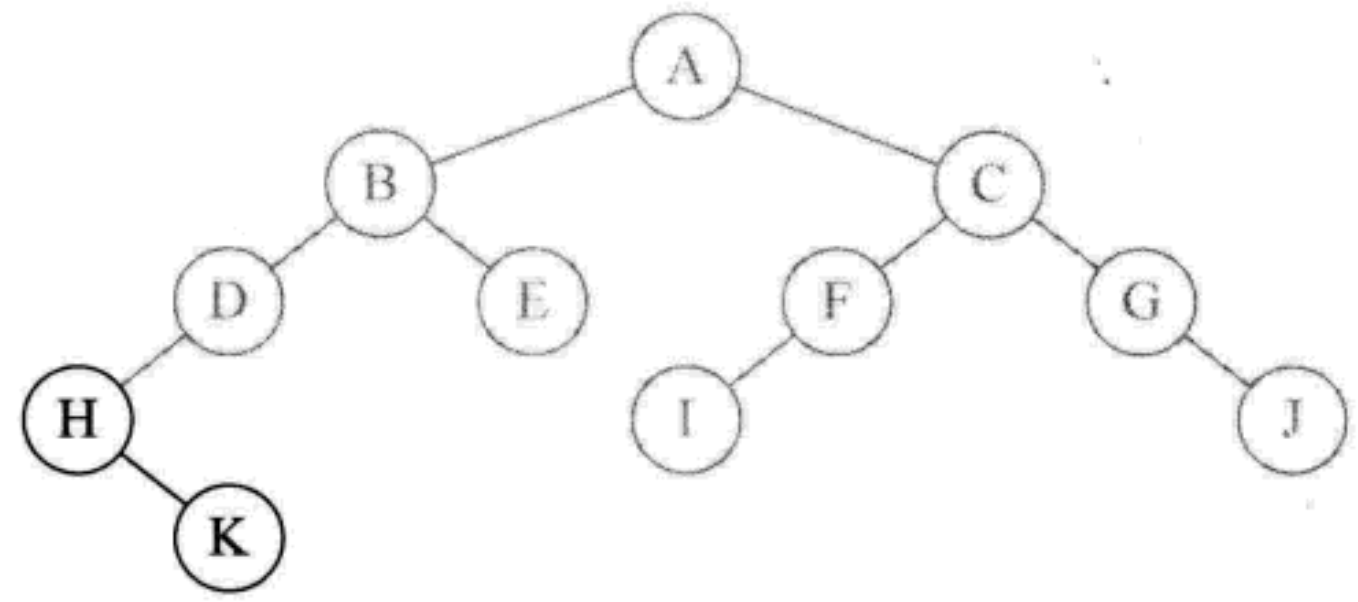
- Because K has no right node, the function of returning. Printing H node is completed, and the letter D is returned
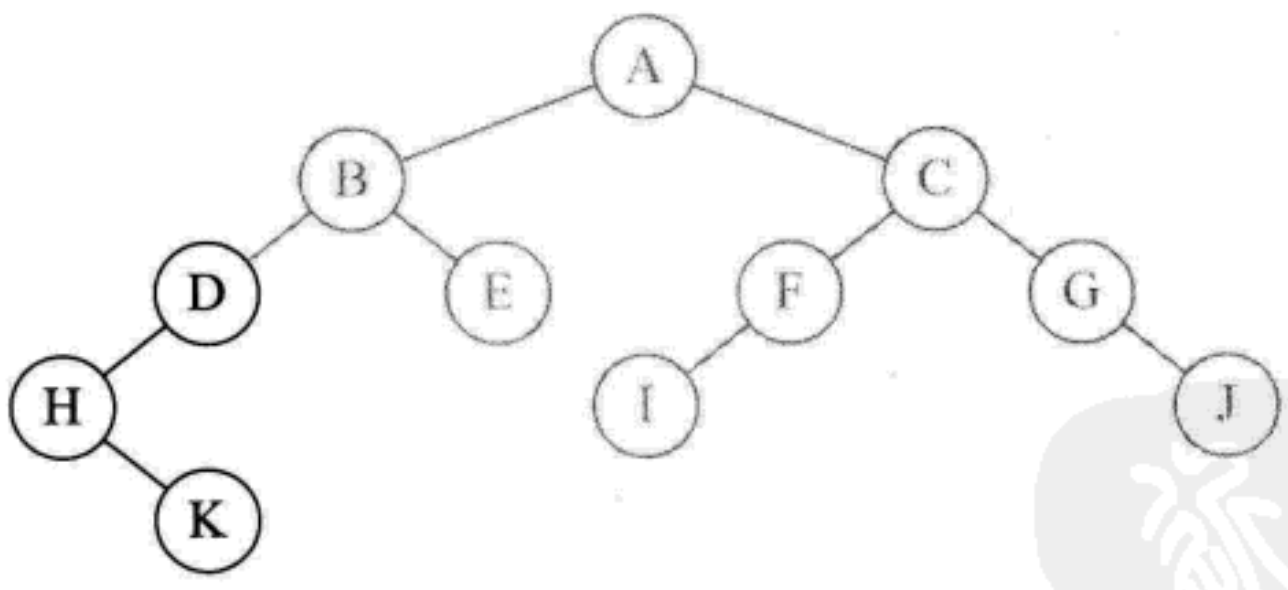
- Node D has no right child, so it returns. Print B

- Call inOrderTraversal(root.right) to access the right node e of node B. because e has no left child, print E
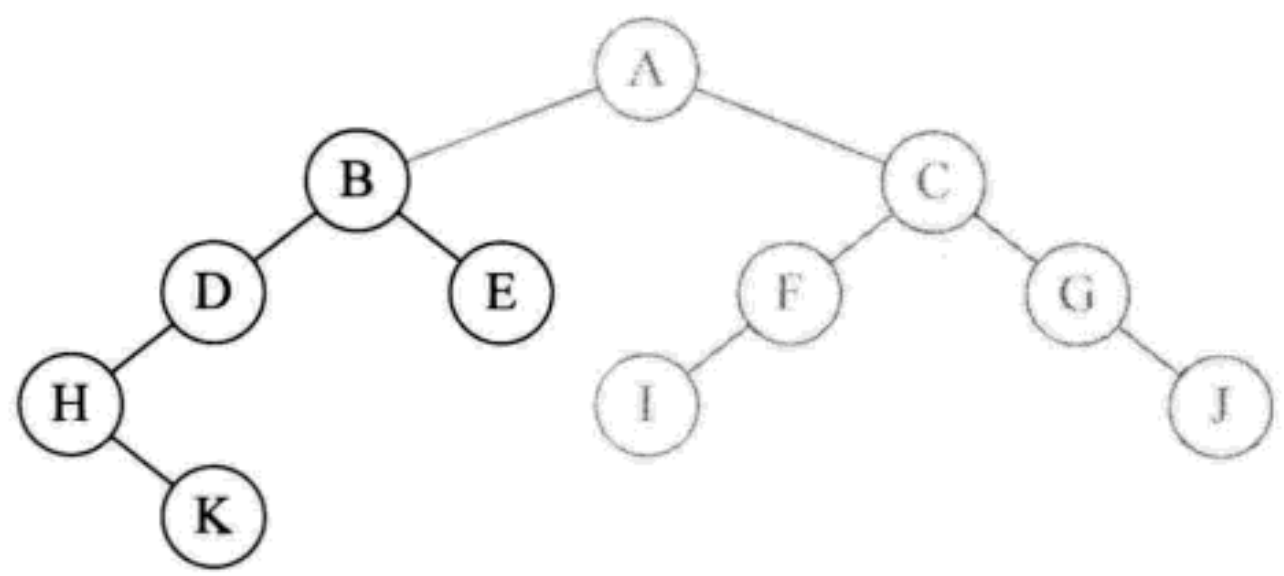
- Node E has no right child and returns to Shanghai. After the function of printing B is executed, it returns to the place where we first executed inOrderTraversal(root) and prints the letter A
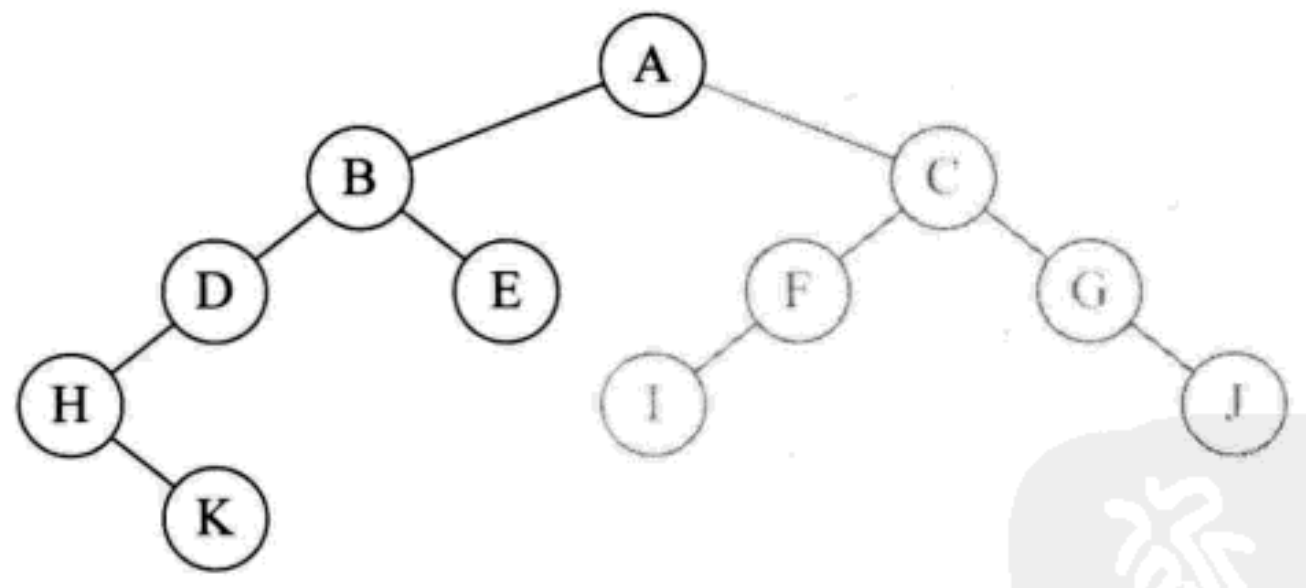
- Call inOrderTraversal(root.right), access the right child C of node A, and then recursively access the left child F of C and the left child I of F. because I has no right child, print I. then print F, C, G and j respectively
Order traversal in iteration
/*
1.Create a stack first
2.Root node stack
3.Loop stack top element
4.The left subtree is collectively stacked before entering the right subtree
5.You should pay attention to the judgment of the outermost while loop. Because cur= cur.right will lead to cur == nulll, you are adding one! Judgment of stack.empty()
*/
private static void inOrderTraversalNo(BinaryTreeNode root) {
if (root == null) {
return;
} else {
Stack<BinaryTreeNode> stack = new Stack<>();
BinaryTreeNode cur = root;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
System.out.print(cur.val + " ");
cur = cur.right;
}
}
}
H K D B E A I F C G J
Demonstrate the sequence traversal steps in an iteration
3.1.3.2 left and right roots of post order traversal algorithm]
OJ topic link
Recursive postorder traversal
/*
OJ: adopt
*/
class Solution {
List<Integer> list = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if(root == null){
return list;
}else{
postorderTraversal(root.left);
postorderTraversal(root.right);
list.add(root.val);
return list;
}
}
}
private static void postOrderTraversal(BinaryTreeNode root) {
if (root == null) {
return;
} else {
postOrderTraversal(root.left);
postOrderTraversal(root.right);
System.out.print(root.val + " ");
}
}
Demonstrate recursive postorder traversal steps
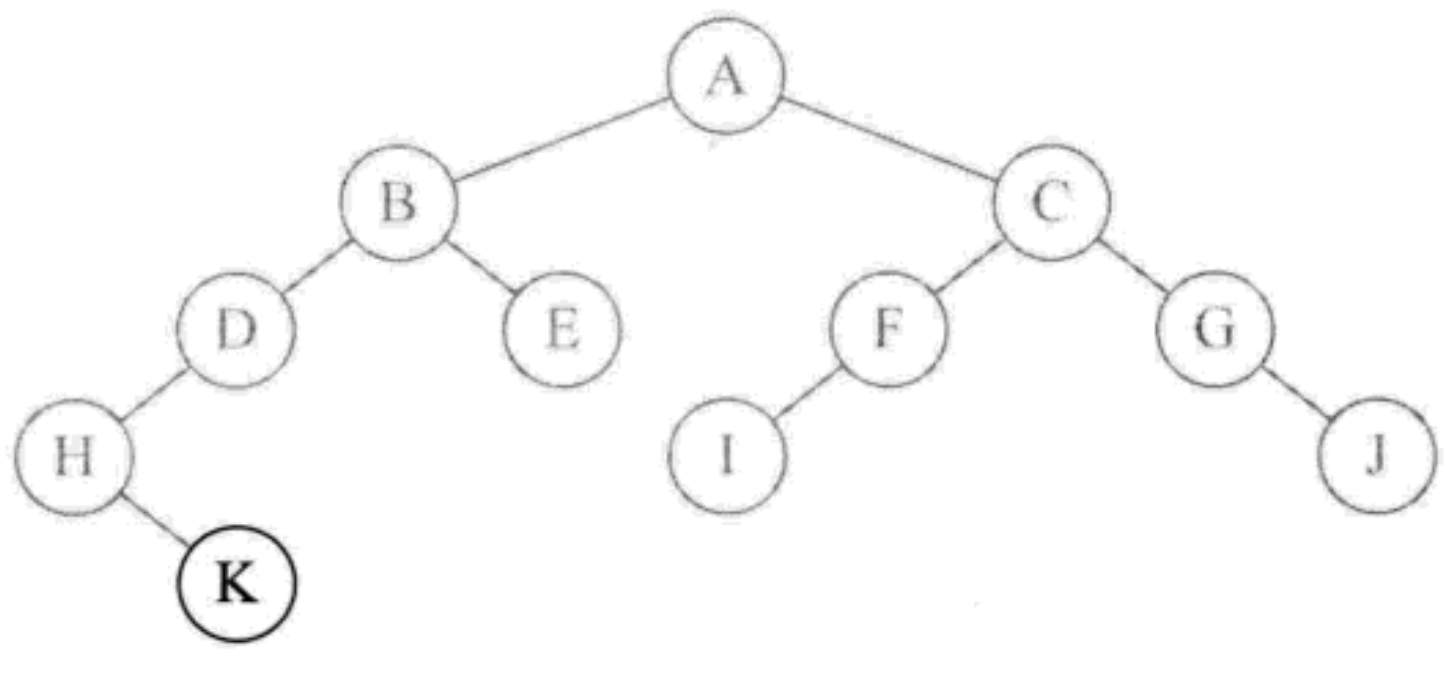
- After the sequence traversal, first recurse the left subtree, from the root node a - > b - > D - > H, node h has no left children, and then check the right child K of H. because node K has no left and right children, K is printed
- After printing, K returns to the program System.out.print(root.val + ""); which executes printing H;, Print h node
- The subsequent analysis steps and all depend on whether the returned node has left and right subtrees and whether the traversal is completed: after traversal, the root node will be output, otherwise the traversal will continue
Sequential traversal after iteration
/*
Similar to middle order traversal
1.The outer cycle still needs to be added! stack.empty() to drive the loop
2.Set the printed node to null, and judge whether the node has been printed
3.judge
overtime
*/
private static void postOrderTraversalNo(BinaryTreeNode root) {
if (root == null) {
return;
} else {
Stack<BinaryTreeNode> stack = new Stack<>();
BinaryTreeNode cur = root;
BinaryTreeNode prev = null;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.peek();
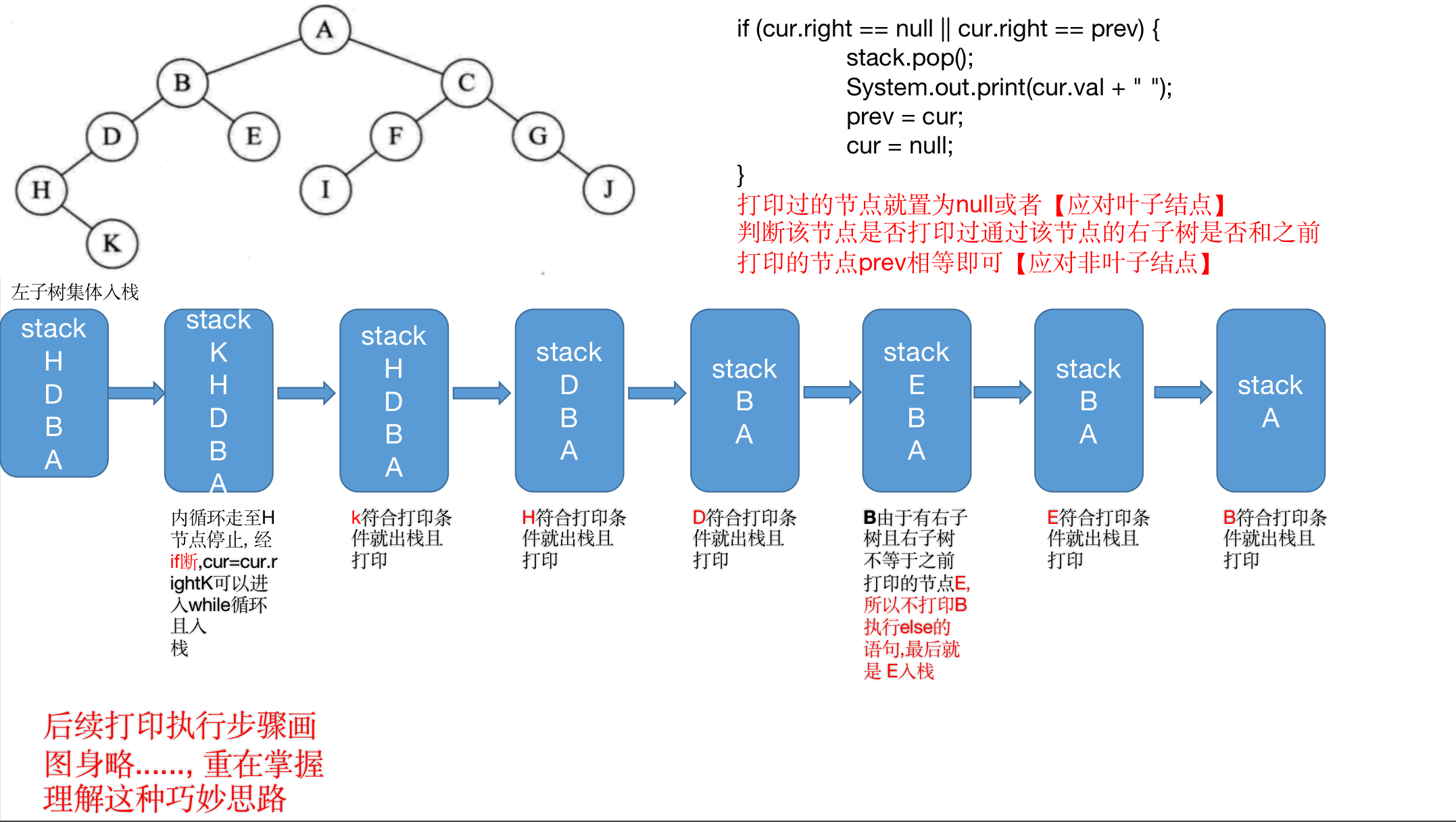
if (cur.right == null || cur.right == prev) {
stack.pop();
System.out.print(cur.val + " ");
prev = cur;
cur = null;
} else {
cur = cur.right;
}
}
}
}
K H D E B I F J G C A
Demonstrate sequential traversal steps after iteration
3.1.3.2 sequence traversal algorithm: top to bottom, left to right
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
// 1. Return empty box
List<List<Integer>> list = new ArrayList<>();
if(root == null){
return list;
}else{
// 2. Queue village coarse
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
List<Integer> tmp = new ArrayList<>();
while(size-- > 0){
TreeNode top = queue.poll();
tmp.add(top.val);
if(top.left != null){
queue.offer(top.left);
}
if(top.right != null){
queue.offer(top.right);
}
}
list.add(tmp);
}
return list;
}
}
}
[[A], [B, C], [D, E, F, G], [H, I, J], [K]]
Demonstrate the code execution steps in the OJ exercise
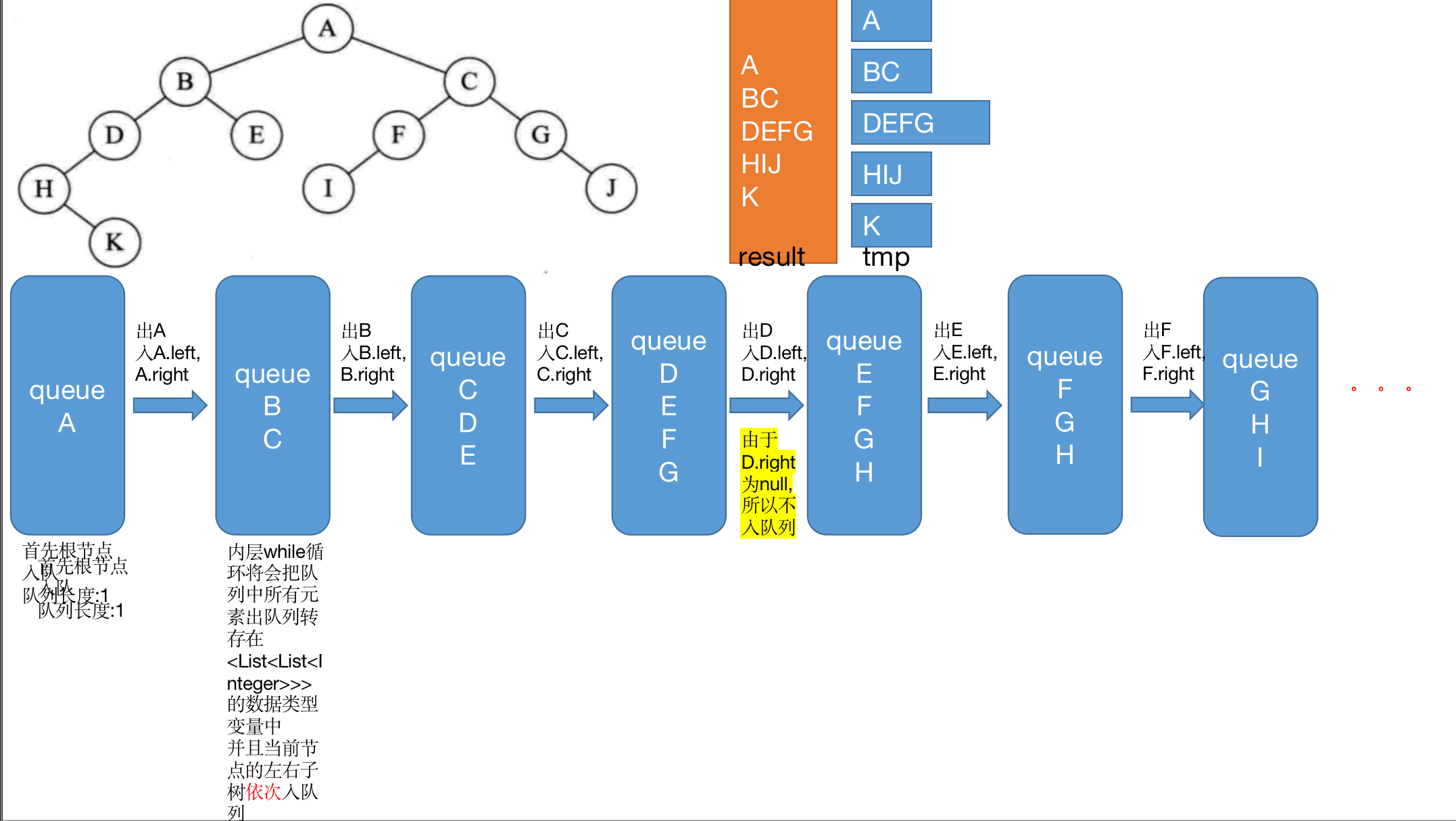
Normal sequence output
/*
1.Create a queue first
2.Put the root node in the queue
3.Cycle through all queue elements
4.Add current element to internal list
4.Then put the left subtree of the current element into the queue and then into the right subtree
5.The large ret adds the list after each new element is added
*/
private static void levelOrder(BinaryTreeNode root) {
if (root == null) {
return;
} else {
Queue<BinaryTreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
BinaryTreeNode top = queue.poll();
System.out.print(top.val + " ");
if (top.left != null) {
queue.offer(top.left);
}
if (top.right != null) {
queue.offer(top.right);
}
}
}
}
A B C D E F G H I J K
3.2 establishment of binary tree
3.2.1 construction of binary tree in pre order and middle order
class Solution {
private int findInorderIndex(int[] inorder, int inbegin, int inend, int key){
for(int i=inbegin; i<=inend; ++i){
if(inorder[i] == key){
return i;
}
}
return -1;
}
private TreeNode buildTreeChild(int[] preorder, int[] inorder, int inbegin, int inend){
if(inbegin > inend){
return null;
}else{
TreeNode root = new TreeNode(preorder[preIndex++]);
int rootIndex = findInorderIndex(inorder, inbegin, inend, root.val);
root.left = buildTreeChild(preorder, inorder, inbegin, rootIndex-1);
root.right = buildTreeChild(preorder, inorder, rootIndex+1, inend);
return root;
}
}
private int preIndex = 0;
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder == null || inorder == null){
return null;
}else{
return buildTreeChild(preorder, inorder, 0, inorder.length-1);
}
}
}
At that time, the principle of recursion was also used to establish the binary tree, but the code of the printed node was replaced by the operation of generating the node and assigning a value to the node
The first node of the preorder traversal must be the root node, so we divide the left and right subtrees of the root node in the preorder traversal, and then recursively find the root node and divide the left and right subtrees. The termination condition of recursion is that the left of the interval must be greater than the right of the interval
Code idea:
- Judge whether one of the pre sequence or middle sequence is null [ special case handling ]
- Using buildTreeChild function to return root node
- First construct the root node, and then recursively construct the left subtree and right subtree
- The last root returned after all recursion is the root node of the tree
Demonstration diagram
- The first search is the root node of preorder[preIndex] (the preIndex value is 0)
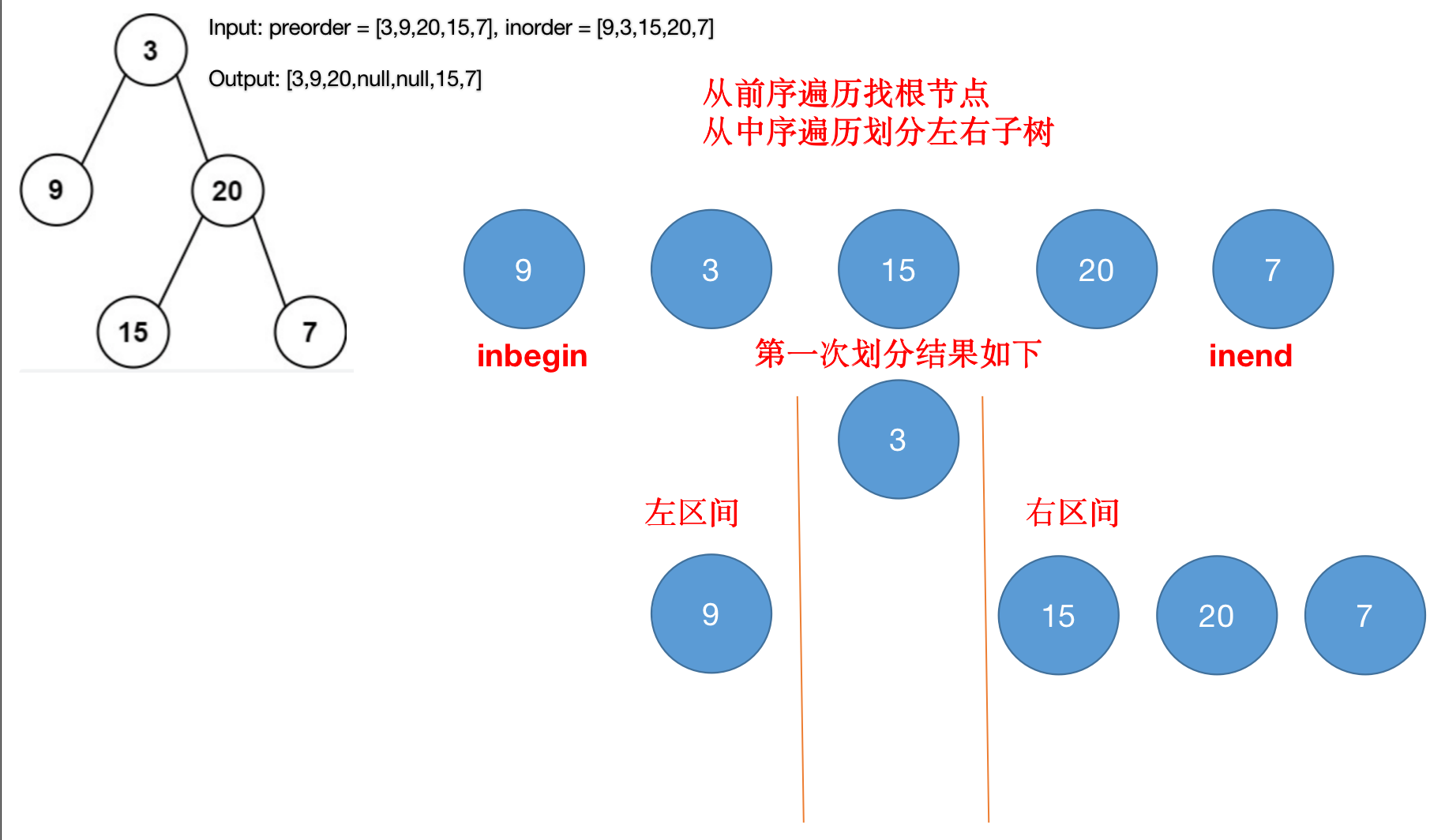
- During the second partition, the new inend is rootIndex-1, so the resulting if (in begin > inend) return; The program returns to execute root.right = buildTreeChild(preorder, inorder, rootIndex+1, inend);
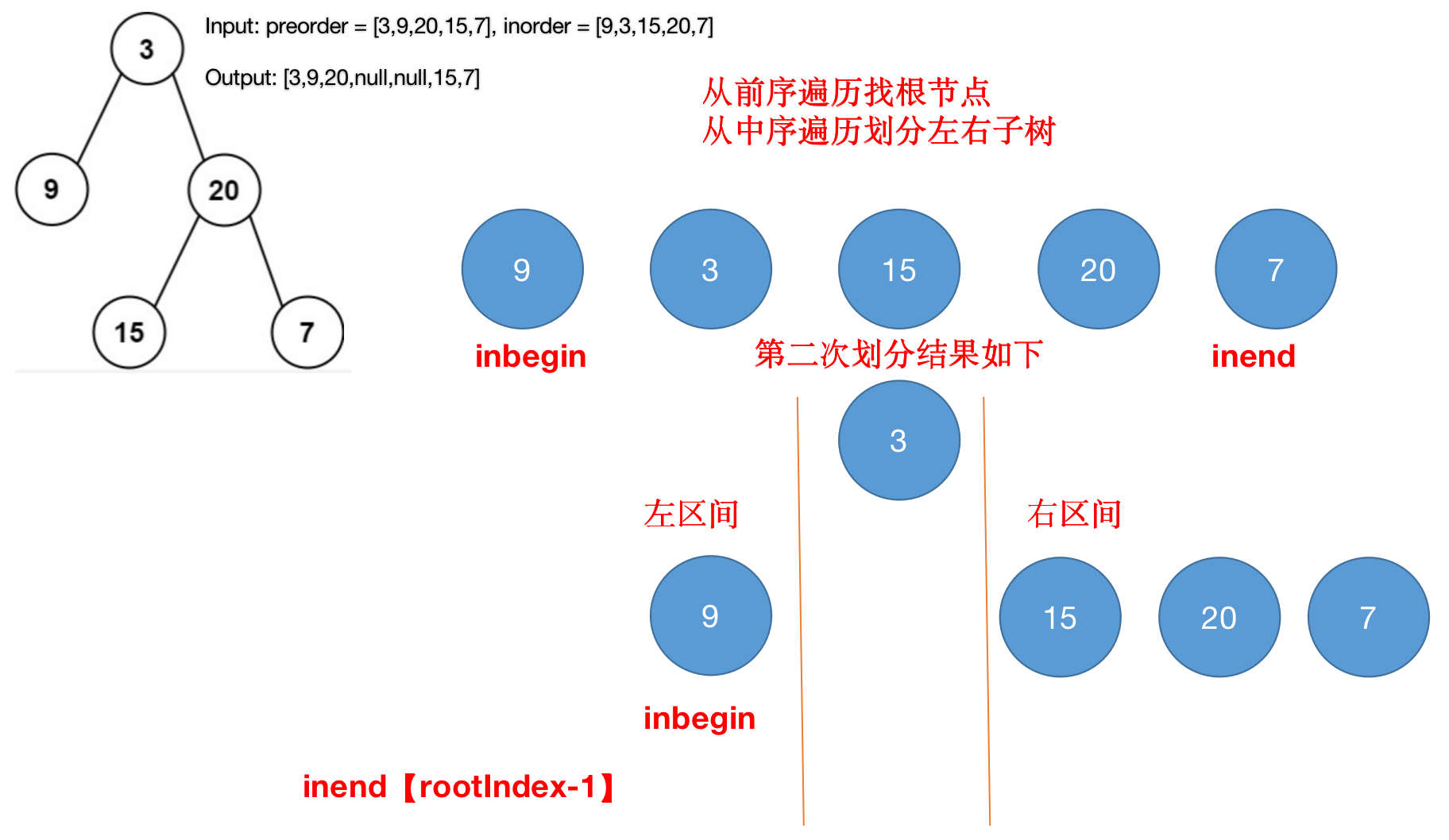
- Third division
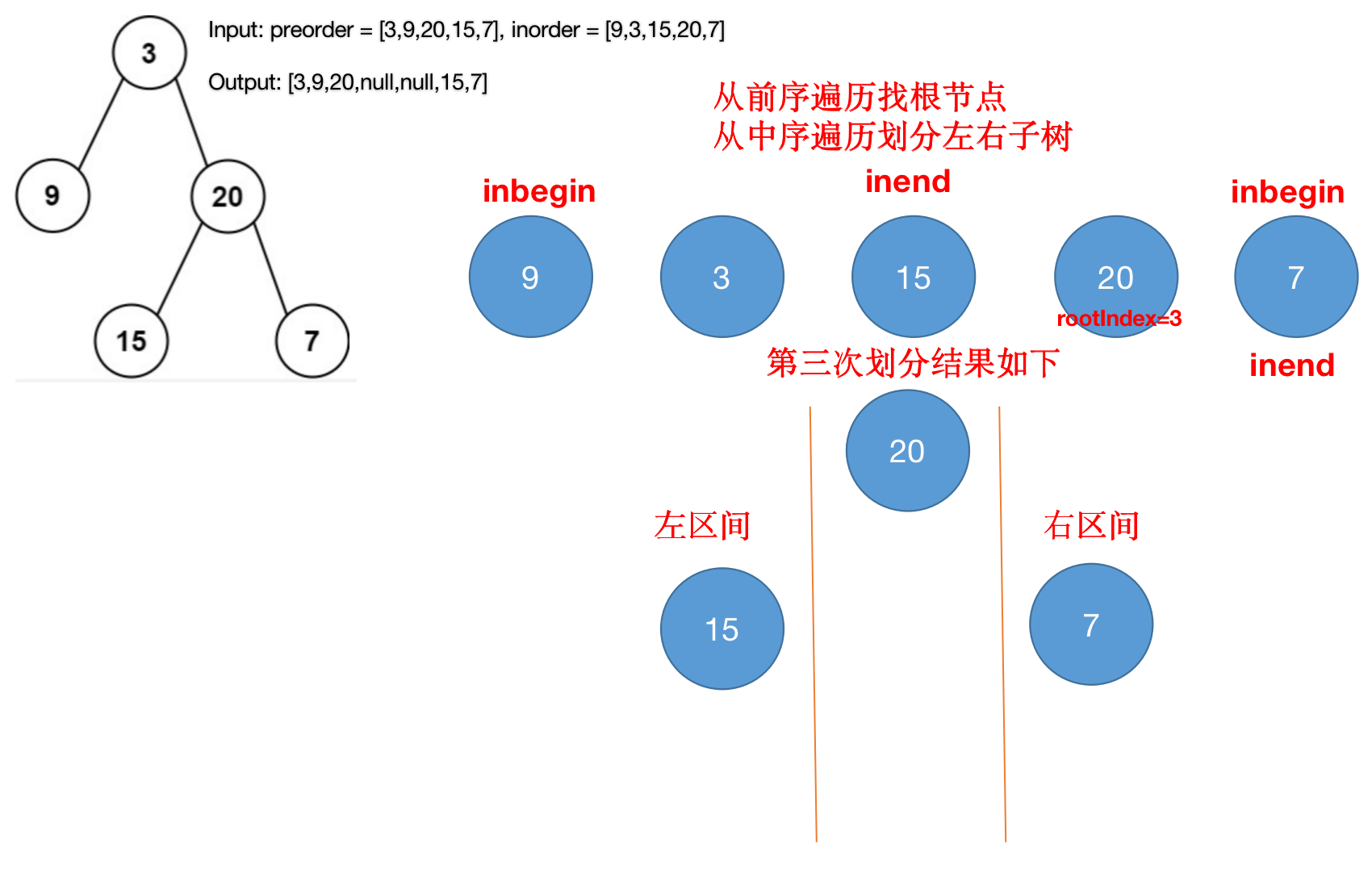
- comprehensive

3.2.2 constructing binary tree in middle order and later order
class Solution {
private int postIndex = 0;
private int findInorderIndex(int[] inorder, int inbegin, int inend, int key){
for(int i=inbegin; i<=inend; ++i){
if(inorder[i] == key){
return i;
}
}
return -1;
}
private TreeNode buildTreeChild(int[] inorder, int[] postorder, int inbegin, int inend){
if(inbegin > inend){
return null;
}else{
TreeNode root = new TreeNode(postorder[postIndex--]);
int rootIndex = findInorderIndex(inorder, inbegin, inend, root.val);
root.right = buildTreeChild(inorder, postorder, rootIndex+1, inend);
root.left = buildTreeChild(inorder, postorder, inbegin, rootIndex-1);
return root;
}
}
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder == null || postorder == null){
return null;
}else{
postIndex = postorder.length-1;
return buildTreeChild(inorder, postorder, 0, postIndex);
}
}
}
Post order traversal has the same idea as pre order change, but attention should be paid to the order [the last post order traversal is the root, and the first pre order traversal is the root]
Demonstration diagram
From the back to the front, the root node is the right node, so first build the right subtree and then the left subtree. The idea of traversal recursion is the same as the above, which will not be described here

The properties of a binary tree are summarized
- Known preorder traversal and inorder traversal, we can determine the only binary tree
- Given the middle order traversal and post order traversal, the unique binary tree can be determined
Thinking: given the preorder traversal and postorder traversal, can we build a unique binary tree
No, the reason is very simple. For example, the preorder traversal of a binary tree is ABC, and the postorder traversal is CBA. We can determine that the root node is a, but we can't determine the left and right subtrees of A. this tree has the following four possibilities

3.2.3 create string from binary tree
Solution 1
- The left subtree is processed first, and then the right subtree is processed
- Add brackets one by one according to the requirements of the topic
class Solution {
private void tree2strChild(TreeNode root, StringBuffer stringBuffer){
if(root == null){
return;
}else{
stringBuffer.append(root.val);
// 1. Processing left subtree
if(root.left == null){
if(root.right == null){
return;
}else{
stringBuffer.append("()");
}
}else{
stringBuffer.append("(");
tree2strChild(root.left, stringBuffer);
stringBuffer.append(")");
}
// 2. Processing right subtree
if(root.right == null){
return;
}else{
stringBuffer.append("(");
tree2strChild(root.right, stringBuffer);
stringBuffer.append(")");
}
}
}
public String tree2str(TreeNode root) {
if(root == null){
return "";
}else{
StringBuffer stringBuffer = new StringBuffer();
tree2strChild(root, stringBuffer);
return stringBuffer.toString();
}
}
}
Solution 2
Less code, easy to understand, but low efficiency
- Add parentheses in the form of recursive preorder traversal
- After adding, delete the first and last parentheses
class Solution {
private StringBuffer stringBuffer = null;
private void tree2strChild(TreeNode root){
if(root == null){
return;
}else{
stringBuffer.append("("+root.val);
tree2strChild(root.left);
if(root.left == null && root.right != null){
stringBuffer.append("()");
}
tree2strChild(root.right);
stringBuffer.append(")");
}
}
public String tree2str(TreeNode root) {
if(root == null){
return "";
}else{
stringBuffer = new StringBuffer();
tree2strChild(root);
stringBuffer.deleteCharAt(0);
stringBuffer.deleteCharAt(stringBuffer.length()-1);
return stringBuffer.toString();
}
}
}
3.2.4 pre order traversal of strings to build a binary tree
import java.util.Scanner;
import java.util.Stack;
class TreeNode{
char val;
TreeNode left;
TreeNode right;
TreeNode(char val){
this.val = val;
}
}
public class Main{
// 1. The middle order traversal is carried out in an iterative manner
private static void inOrderTraversal(TreeNode root){
if(root == null){
return;
}else{
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while(cur != null || !stack.empty()){
// 2. Left subtree collective stack
while(cur != null){
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
System.out.print(cur.val + " ");
cur = cur.right;
}
}
}
private static int index = 0;// Record the printed string subscript. Because it is recursive, you should use global variables instead of local variables
private static TreeNode createTree(String str){
if(str == null){
return null;
}else{
TreeNode root = null;
// 1. Cross the empty node
if(str.charAt(index) == '#'){
++index;
}else{
// 2. Recursively construct a binary tree in the form of left and right preorder roots
root = new TreeNode(str.charAt(index++));
root.left = createTree(str);
root.right = createTree(str);
}
return root;
}
}
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
while(scanner.hasNext()){
String str = scanner.next();
TreeNode root = createTree(str);
inOrderTraversal(root);
System.out.println();
}
}
}
3.2.5 merge binary tree
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
// 1. If a node is null, another node will be returned
if(root1 == null){
return root2;
}else if(root2 == null){
return root1;
}else{
// 2. If both nodes are not null, start merging the binary tree
TreeNode root = new TreeNode(root1.val+root2.val);
root.left = mergeTrees(root1.left, root2.left);
root.right = mergeTrees(root1.right, root2.right);
return root;
}
}
}
3.2.6 incremental binary tree
class Solution {
private TreeNode cur = null;
private void inOrderTraversal(TreeNode root){
if(root == null){
return;
}else{
//1. Left
inOrderTraversal(root.left);
// 2. Root
cur.right = root;
root.left =
// 3. Right
inOrderTraversal(root.right);
}
}
public TreeNode increasingBST(TreeNode root) {
if(root == null){
return null;
}else{
// 1. The puppet node is used to save the location of the cur node for return
TreeNode newRoot = new TreeNode(-1);
// 2. Mobile node
cur = newRoot;
inOrderTraversal(root);
return newRoot.right;
}
}
}
3.3 analysis of classic topics
3.3.1 number of nodes
/*
Find the number of nodes
Traversal idea: recursion increases by 1 every time it traverses [Online OJ may overturn: first call gerSize1 method with a small tree, and then call getSize1 with a large tree]
Subquestion idea: return 1+func()... With its own return value
*/
private static int size = 0;
private static void getSize1(BinaryTreeNode root) {
if (root == null) {
return;
} else {
++size;
getSize1(root.left);
getSize1(root.right);
}
}
private static int getSize2(BinaryTreeNode root) {
if (root == null) {
return 0;
} else {
return 1 + getSize2(root.left) + getSize2(root.right);
}
}
3.3.2 number of leaf nodes
/*
Find the number of leaf nodes
Traversal idea: recursive traversal
Subquestion idea: return 1+func()
*/
private static int leaftSize = 0;
private static void getLeafSize1(BinaryTreeNode root) {
if (root == null) {
return;
} else {
if (root.left == null && root.right == null) {
++leaftSize;
} else {
getLeafSize1(root.left);
getLeafSize1(root.right);
}
}
}
private static int getLeafSize2(BinaryTreeNode root) {
if (root == null) {
return 0;
} else {
if (root.left == null && root.right == null) {
return 1;
} else {
return getLeafSize2(root.left) + getLeafSize2(root.right);
}
}
}
3.3.3 number of nodes in layer k
private static int getKLevelSize(BinaryTreeNode root, int k) {
if (root == null || k < 1) {
return 0;
} else {
if (k == 1) {
return 1;
} else {
return getKLevelSize(root.left, k - 1) + getKLevelSize(root.right, k - 1);
}
}
}
3.3.4 find the node where val is located
private static BinaryTreeNode find(BinaryTreeNode root, String val) {
if (root == null) {
return null;
} else {
if (root.val.equals(val)) {
return root;
} else {
BinaryTreeNode ret = find(root.left, val);
if (ret != null && ret.val.equals(val)) {
return ret;
}
ret = find(root.right, val);
if (ret != null && ret.val.equals(val)) {
return ret;
}
return null;
}
}
}
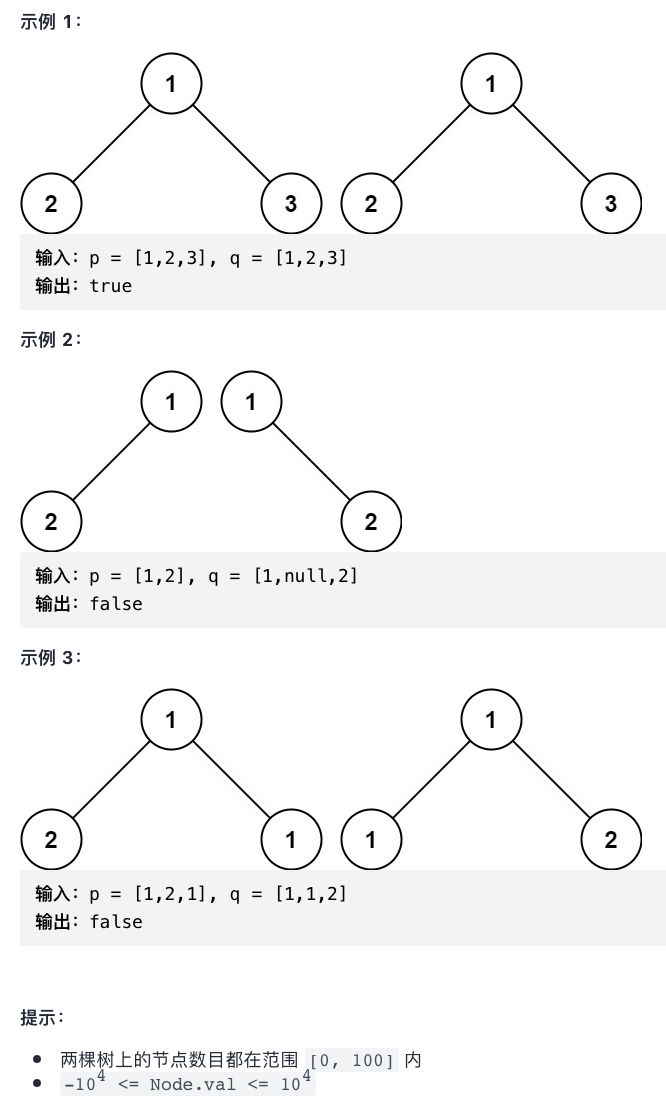
3.3.5 same tree
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
// 1. Both are null: it means that the previous node and node values are equal, so they are equal; Or two empty nodes are equal
if(p == null && q == null){
return true;
// 2. One node is traversed, but the other node is not null, so it is false
}else if(p == null || q == null){
return false;
}else{
// 3. false if the node values are not equal
if(p.val != q.val){
return false;
}else{
// 4. Perform the next comparison recursively
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}
}
3.3.6 another sub tree
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
// 1. Both are null: it means that the previous node and node values are equal, so they are equal; Or two empty nodes are equal
if(p == null && q == null){
return true;
// 2. One node is traversed, but the other node is not null, so it is false
}else if(p == null || q == null){
return false;
}else{
// 3. false if the node values are not equal
if(p.val != q.val){
return false;
}else{
// 4. Perform the next comparison recursively
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}
}
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
// 1. Two nullnull s are subtrees; Traverse the subtree of the leaf node [although it does not exist], indicating that the previous traversals are equal
if(root == null && subRoot == null){
return true;
}else if(root == null && subRoot != null || root != null && subRoot == null){
return false;
}else{
// 1. If two nodes are not empty and equal, they are subtrees
if(isSameTree(root, subRoot)){
return true;
// 2. Recursively judge whether it is a subtree
}else if(isSubtree(root.left, subRoot)){
return true;
}else if(isSubtree(root.right, subRoot)){
return true;
}else{
return false;
}
}
}
}
3.3.7 maximum depth of binary tree
class Solution {
public int maxDepth(TreeNode root) {
if(root == null){
return 0;
}else{
// 1. Calculate the height of the left subtree
int left = maxDepth(root.left)+1;
// 2. Calculate the height of the right subtree
int right = maxDepth(root.right)+1;
if(left>right){
return left;
}else{
return right;
}
}
}
}
3.3.8 balanced binary tree
class Solution {
private int maxDepth(TreeNode root){
if(root == null){
return 0;
}else{
int left = 1+maxDepth(root.left);
int right = 1+maxDepth(root.right);
return left>right?left:right;
}
}
public boolean isBalanced(TreeNode root) {
if(root == null){
return true;
}else{
int left = maxDepth(root.left);
int right = maxDepth(root.right);
if(Math.abs(left-right)>1){
return false;
}else{
return isBalanced(root.left) && isBalanced(root.right);
}
}
}
}
// 1. Optimized code: calculate the height difference between the left and right subtrees while calculating the height, without recursion twice
class Solution {
private int maxDepth(TreeNode root){
if(root == null){
return 0;
}else{
int left = maxDepth(root.left);
int right = maxDepth(root.right);
if(left >= 0 && right >= 0 && Math.abs(left-right)<=1){
return Math.max(left, right)+1;
}else{
return -1;
}
}
}
public boolean isBalanced(TreeNode root) {
return maxDepth(root) > -1;
}
}
3.3.9 symmetric binary tree
class Solution {
private boolean isSameTree(TreeNode leftTree, TreeNode rightTree) {
if (leftTree == null && rightTree == null) {
return true;
} else if (leftTree != null && rightTree == null || leftTree == null && rightTree != null) {
return false;
} else {
if (leftTree.val != rightTree.val) {
return false;
} else {
/*
1. The previous judgment steps are similar to comparing whether the binary tree is the same
2. After that, the left of the left tree and the right of the right tree should be compared; Is the right of the left tree the same as the left of the right tree
*/
return isSameTree(leftTree.left, rightTree.right) && isSameTree(leftTree.right, rightTree.left);
}
}
}
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true;
} else {
return isSameTree(root.left, root.right);
}
}
}
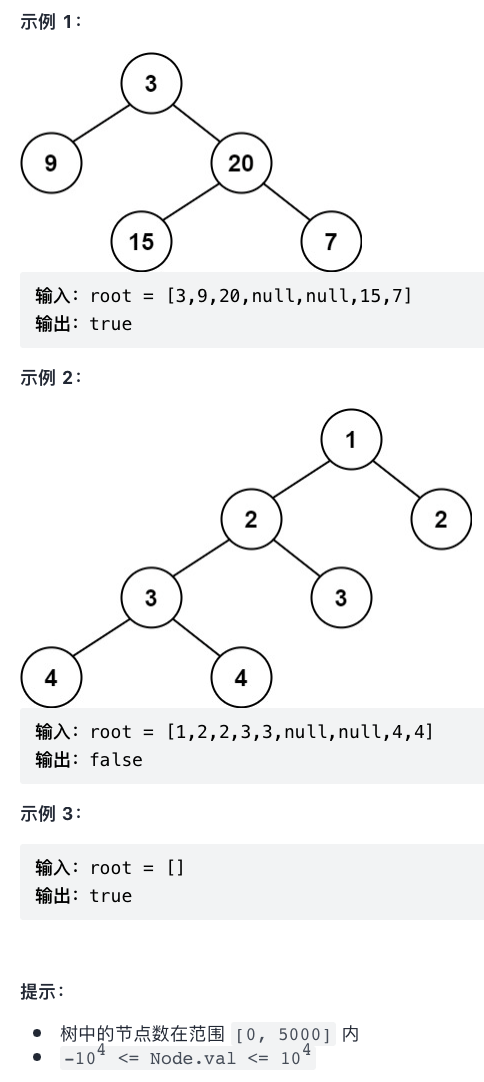
3.3.10 completeness test of binary tree
Use the queue feature to judge whether all the nodes are in the queue (including null nodes) and then out of the queue
/*
1. When a null node is encountered, it indicates that all complete binary trees have been traversed and exits
2. Pop up the element slowly at the end of the queue. If it is not null, it indicates that it is not a complete binary tree
*/
class Solution {
public boolean isCompleteTree(TreeNode root) {
if(root == null){
return true;
}else{
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
// 1. Stop entering the queue until a null node is encountered
while(!queue.isEmpty()){
TreeNode top = queue.poll();
if(top != null){
queue.offer(top.left);// When the program reaches the leaf node, it will also bring the null node into the queue. If a non null node is encountered during the subsequent peekpeek detection, it means that there are other leaf nodes after the null node is encountered. At this time, it must not be a complete binary tree
queue.offer(top.right);
}else{
break;
}
}//When the program is executed here, it indicates that all nodes have been stored in the queue
// 2. The node goes out of the queue and peek detects whether the element is null
while(!queue.isEmpty()){
TreeNode top = queue.peek();
if(top != null){
return false;
}else{
queue.poll();//Out of queue
}
}
return true;
}
}
}
Optimization: simple and efficient judgment by comparing the number of nodes and subscripts
class Solution {
private int n=0, p=0;
private boolean dfs(TreeNode root, int k){
if(root == null){
return true;// 1. Node traversal is completed
}else if(k > 100){
return false;// 2. Topic tip: there will be 1 to 100 nodes in the tree
}else{
++n;// 3. Every time you traverse, the number of nodes will increase by one, and the subscript of the current node will be recorded
p = Math.max(p, k);// 4. Because there are left and right subtrees, the maximum subscript should be selected each time
return dfs(root.left, 2*k) && dfs(root.right, 2*k+1);
}
}
public boolean isCompleteTree(TreeNode root) {
if(root == null){
return true;
}else{
if(!dfs(root, 1)){
return false;// 1. false is returned when the number of nodes exceeds 100
}else{
return n == p;// 2. If it does not exceed 100 nodes, judge whether the number of nodes is equal to the maximum subscript number
}
}
}
}
3.3.11 nearest father-in-law ancestor of binary tree
/*
left == null, right == null: return null
left != null, right != null: return root
left == null, right != null: return right
left != null, right == null: return left
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q){
return root;
}else{
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null && right == null){
return null;
}else if(left != null && right == null){
return left;
}else if(left == null && right != null){
return right;
}else{
return root;
}
}
}
}
3.3.12 maximum width of binary tree
class Solution {
public int widthOfBinaryTree(TreeNode root) {
if(root == null){
return 0;
}else{
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int max_width = 0;
while(!queue.isEmpty()){
int cur_width = queue.getLast().val-queue.getFirst().val+1;// 1. Use the value field of the node to record the current queue width
// 2. The left and right subtrees of the head node are queued to prepare for the next width calculation
int count = queue.size();// 3. If the queue size changes from time to time, we should keep the queue size before entering the queue
for(int i=0; i<count; ++i){
TreeNode top = queue.poll();// 4. Leave the queue elements and keep them to pave the way for the subsequent left and right subtrees to enter the queue
if(top.left != null){
queue.offer(top.left);
top.left.val = top.val << 1;// 5. It is based on the nature of binary tree 5 -- left child: 2*i root: i right child: 2*i+1
}
if(top.right != null){
queue.offer(top.right);
top.right.val = (top.val << 1) + 1;
}
}
if(max_width < cur_width){
max_width = cur_width;
}
}
return max_width;
}
}
}
Other languages should consider the following tips: shaping overflow
3.4. Special binary tree problem
3.4.1 search Binary Tree
static class BinaryTreeNode {
// Stored as key value pairs
int key;
int value;
BinaryTreeNode left;
BinaryTreeNode right;
public BinaryTreeNode(int key, int value) {
this.key = key;
this.value = value;
}
}
// Root: represents the root node of the tree. An empty tree is represented by null
private BinaryTreeNode root = null;
//Find: find Value according to Key
private Integer search(int key) {
BinaryTreeNode cur = root;
while (cur != null) {
if (key < cur.key) {
cur = cur.left;
} else if (key > cur.key) {
cur = cur.right;
} else {
return key;
}
}
return null;
}
// insert
private void insert(int key, int value) {
if (root == null) {
root = new BinaryTreeNode(key, value);
} else {
BinaryTreeNode cur = root;
BinaryTreeNode parend = null;
while (cur != null) {
parend = cur;
if (key < cur.key) {
cur = cur.left;
} else if (key > cur.key) {
cur = cur.right;
} else {
return;// There is no equality in binary search tree. If it is equal, it is not necessary to assign a value
}
}
// When the program is executed here, it indicates that the parent node is already the parent node of cur. You can modify the parent node
if (key < parend.key) {
parend.left = new BinaryTreeNode(key, value);
} else {
parend.right = new BinaryTreeNode(key, value);
}
}
}
// Delete: delete by key
private void remove(int key) {
// 1. First find the location corresponding to the key
BinaryTreeNode cur = root;
BinaryTreeNode parent = null;
while (cur != null) {
parent = cur;
if (key < cur.key) {
cur = cur.left;
} else if (key > cur.key) {
cur = cur.right;
} else {
/*
2.Core deletion
Consider that the current cur.left is empty
Is the root node root
Yes: link right subtree
No: then judge whether the currently deleted child node cur is the relationship between the left and right subtrees of its parent node
Consider that cur.right is null
Follow the same idea as the root node of cur.left
Consider that cur.right and cur.left are not empty
Shape shifting shadow removal
*/
if (cur.left == null) {
if (cur == root) {
root = cur.right;
} else if (cur == parent.left) {
parent.left = cur.right;
} else if (cur == parent.right) {
parent.right = cur.right;
}
} else if (cur.right == null) {
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) {
parent.left = cur.left;
} else if (cur == parent.right) {
parent.right = cur.left;
}
} else {
// Specific shape shifting and shadow changing steps
// 1. Find the minimum value in the right subtree and record its parent node
BinaryTreeNode targetParent = cur;
BinaryTreeNode target = cur.right;
while (target.left != null) {// The minimum characteristic is that the left subtree is empty
targetParent = target;
target = target.left;
}
// 2. The program is executed here: targetParent is the parent node of target; Target is the smallest value in the right subtree
// 3. Assign the value of the scapegoat target node to the deletion node
cur.key = target.key;
cur.value = target.value;
// 4. Disconnect the relationship between the end minimum node and establish a new relationship
if (target == targetParent.left) {
targetParent.left = target.right;// The minimum left node is null
} else if (target == targetParent.right) {
targetParent.right = target.right;
}
}
}
}
}
3.4.2 Huffman tree and its application
3.4.1. Huffman tree
What is? Huffman tree
The purpose of Huffman tree is to compress strings. We often use zip, tar, ara... And other compression based on the principle of Huffman tree

Take a common scoring standard for primary and secondary schools
if (a < 60) {
b = "fail,";
} else if (a < 70) {
b = "pass";
} else if (a < 80) {
b = "secondary";
} else if (a < 90) {
b = "good";
} else {
b = "excellent";
}
A good test paper should make most of the students' scores in the medium or good range, and there should be few excellent and failed. The above program needs to make all the scores judge whether they pass, and then get the results step by step. When there is a large amount of data, the efficiency of the algorithm is very low
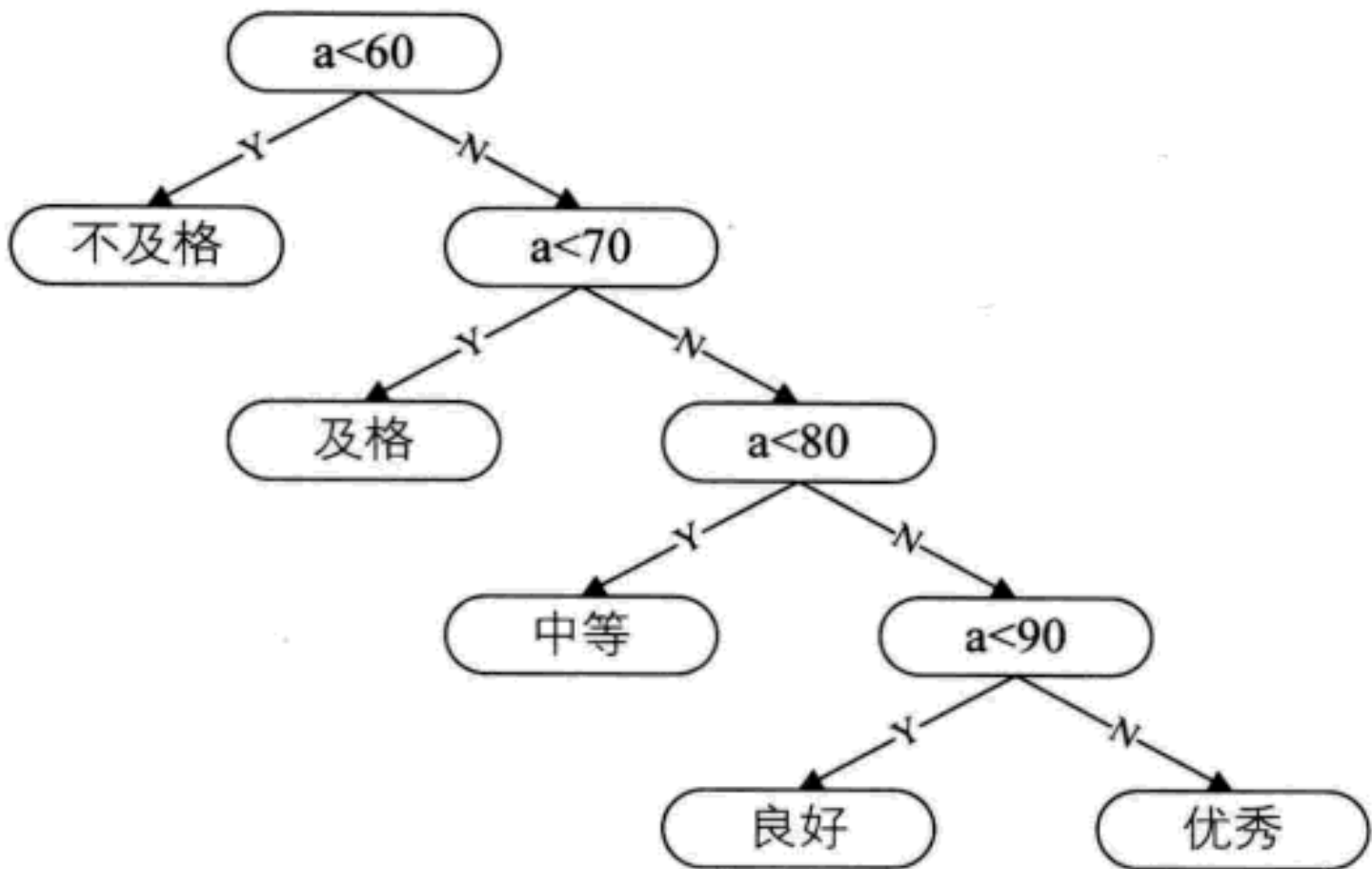
The distribution law of middle school students' scores in real life is shown in the table below

It is obviously unreasonable that the results of more than 70 points, accounting for about 80% of the total, can only be obtained after more than three times of judgment
After careful observation, it is found that the proportion of medium grade (70 ~ 79) is the highest, followed by good grades, and the proportion of failure is the least. The above binary tree is redistributed as follows (it is a bit like searching binary tree, but it is not. Look carefully at the following articles):

3.4.2. Definition and principle of Huffman tree
Simplify two binary trees into binary trees with weighted leaf nodes [A: failed, B: passed, C: medium, D: good, E: excellent]
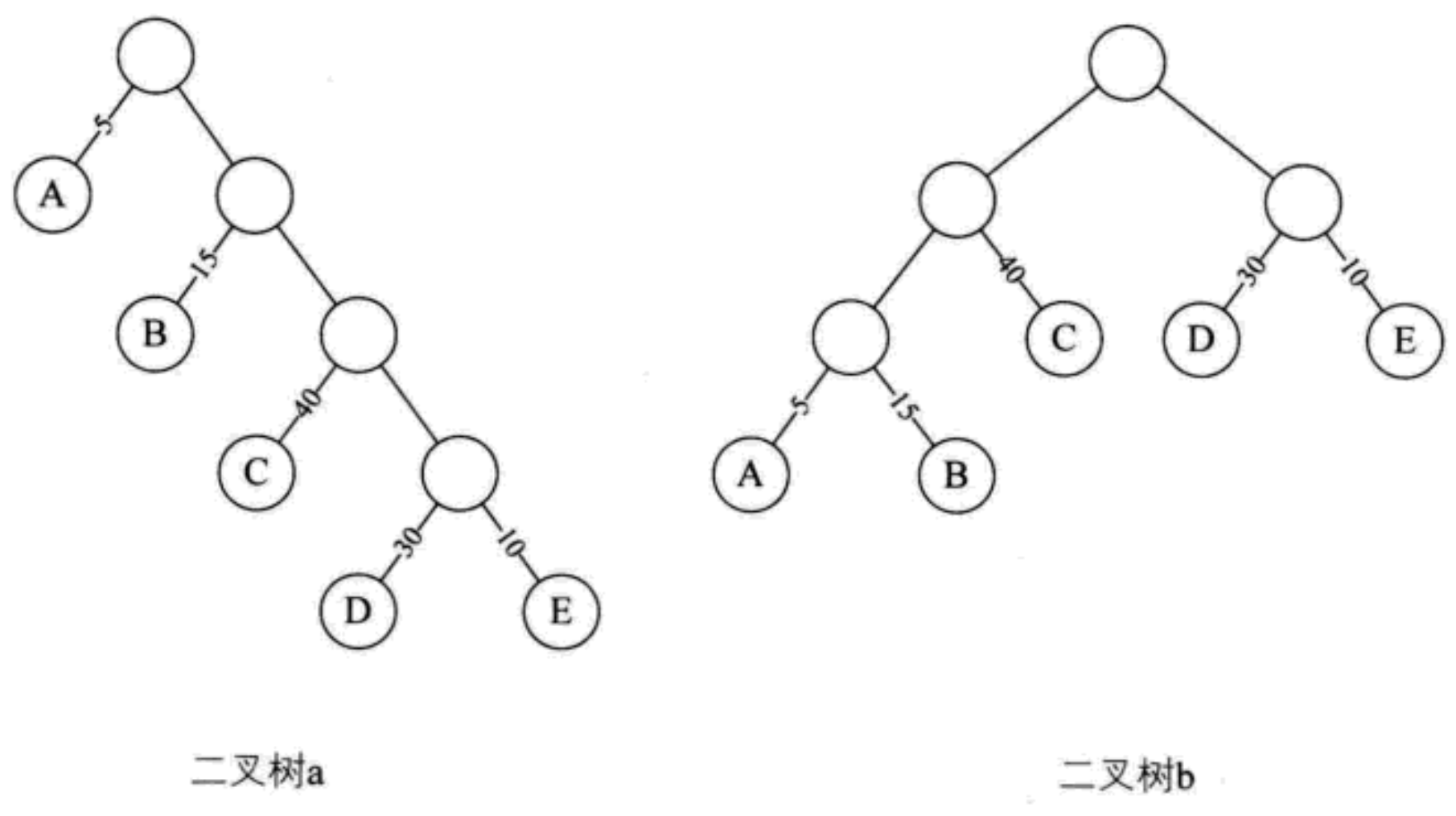
The branch structure from one node to another in the tree is the path between two chickens. The branch tree on the path is called the path length
The path length from root node to node D in binary tree a is 4, and the length from root node to node D in binary tree b is 2
Total length of binary tree a: 1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 = 20
Total length of binary tree b: 1 + 1 + 2 + 2 + 2 + 2 + 3 + 3 = 16
If the weighted node is considered: the product of the path length from the node to the tree root and the weight on the node. The weighted path length of the tree is the sum of the weighted path lengths of all leaf nodes in the tree, which is expressed by WPL. The tree with the smallest WPL is called Huffman tree
Binary tree a WPL: 5 * 1 + 15 * 2 + 40 * 2 + 30 * 4 + 10 * 4 = = 315
Binary tree b WPL: 5 * 3 + 15 * 3 + 40 * 2 + 30 * 2 + 10 * 2 = 220
This result means that if there is 1_ According to the percentile data of 0000 students, the five-level score is calculated. The binary tree a needs 31500 comparisons and the binary tree b needs 2200 comparisons. It is almost 1 / 3 less, and the performance is not improved a little
How to construct Huffman tree?
- First, the leaf nodes with weights are arranged into an ordered sequence from small to large [A5, E10, B15, D30, C40]
- Take the first two minimum full value nodes as the two word nodes of a new node N1. A is the left subtree of N1 and E is the right subtree of N1. Pay attention to the size relationship between the left and right subtrees
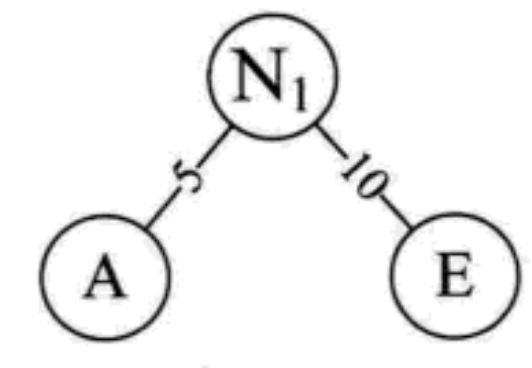
- Replace A and E with N1, insert them into the ordered sequence and keep the arrangement from small to large [N1 15, B15, D30, C40]
- Repeat step 2. Take N1 and B as two word nodes of a new node N2
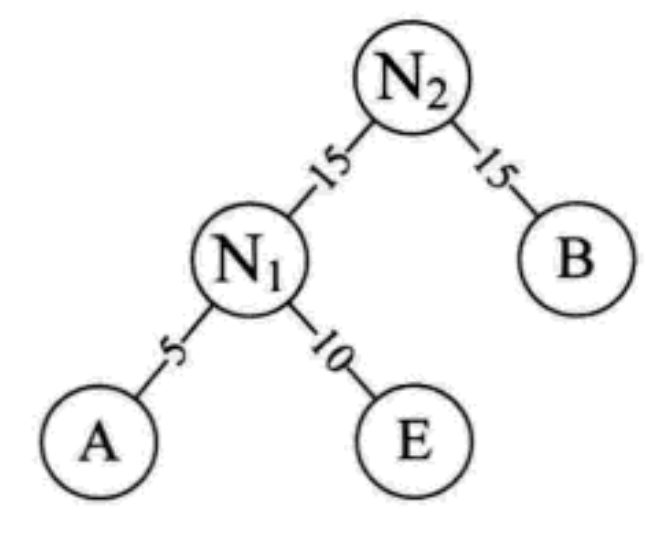
Repeat the sequence in step 3 to replace the minimum value of the sequence, and then repeat step 2 to generate a new node
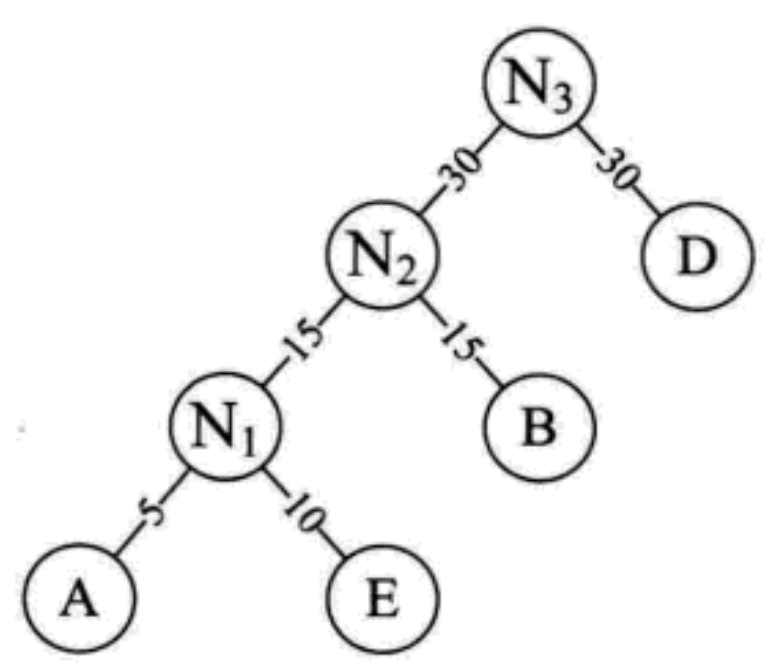
Final effect:
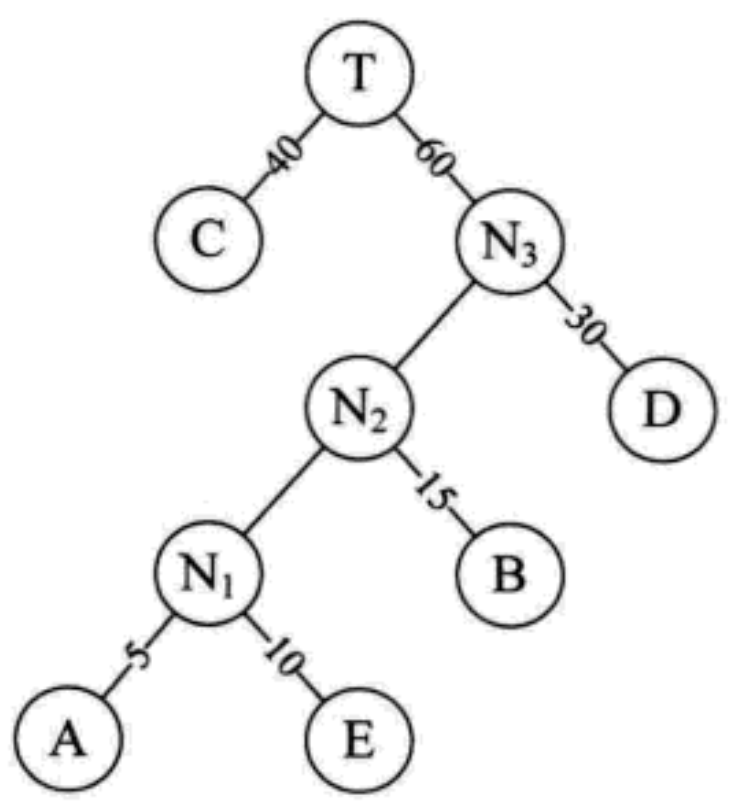
WPL=40 * 1 + 30 * 2 + 15 * 3 + 10 * 4 + 5 * 4 = 205, which is 15 less than the search binary tree, so this is the optimal Huffman tree
3.4.3 Huffman code
Huffman tree is more important to solve the optimization problem of data transmission in long-distance communication (mainly Telegraph)
For example, it is a natural idea to use binary data (0 and 1) to express a text with the content of "BADCADFEED" to be transmitted to others through the network. This text has six letters ABCDEF
The corresponding binary data representation is:

In this way, the real transmission is the encoded "0010000111000000111010011". The other party can accept it and decode it according to three bits per minute. If the content of the article is very long, such a binary string is also terrible
At this point, the Huffman tree should be used
Suppose that the frequency of six letters: A: 27, B: 8, C: 15, D: 15, e: 30 and F: 5 add up to exactly 100%
The left figure shows the process weight of constructing Huffman tree; The figure on the right shows the Huffman tree after changing the weight left subtree to 0 and the right subtree score to 1

At this point, we re encode the six letters

Original code: 001000011101010010010011 [30 characters]
New code: 1001010010101001000111100 [25 characters]
Five characters are missing, which is about 17% [5 / 30 = 0.167]
The more characters, the more obvious the compression effect
The question is: how to parse the Huffman code after receiving it?
In the code, if the length is not 0, that is 1, it is easy to be confused, so it is necessary to design codes with different lengths: the code of any character is not the prefix of the code of another character. This ratio is called prefix coding [01, 1001, 101, 00, 11, 1000 are of different lengths, so it is not easy to be confused]
This is not enough for us to decode conveniently. Therefore, both the receiver and the sender must agree on the same Huffman coding rules during decoding
When receiving 1001010010101001000111100, according to the agreed Huffman coding rules, 1001 gets the first letter B, and the next A01 means the second letter A
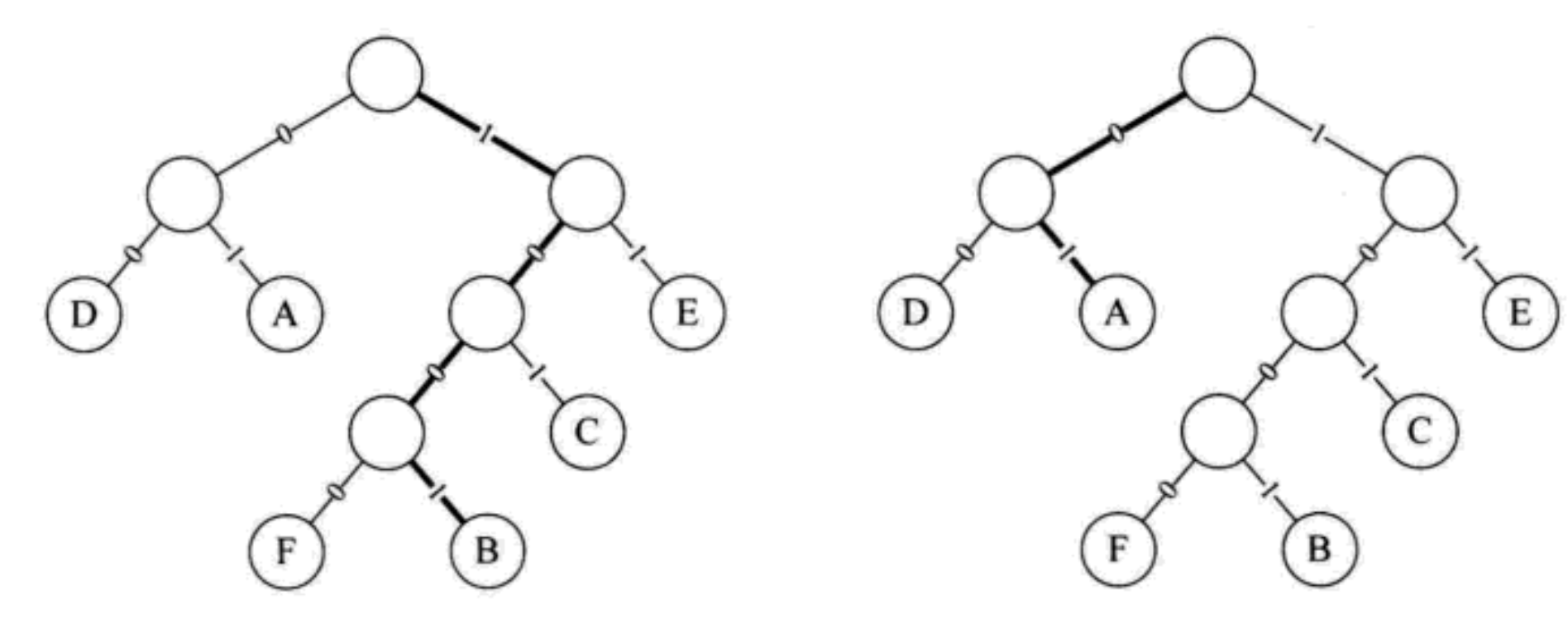
Generally, let the character set to be encoded be {d1,d2,..., dn}, and the number or frequency set of each character in the message be {w1,w2,..., WN}. Take d1,d2,..., dn as the leaf node and w1,w2,..., wn as the weight of the corresponding leaf node to construct a Huffman tree.
It is stipulated that the left branch of Huffman tree represents 0 and the right branch represents 1, then the sequence of 0 and 1 composed of the path branches from the root node to the leaf node is the code of the corresponding characters of the node, which is Huffman code.
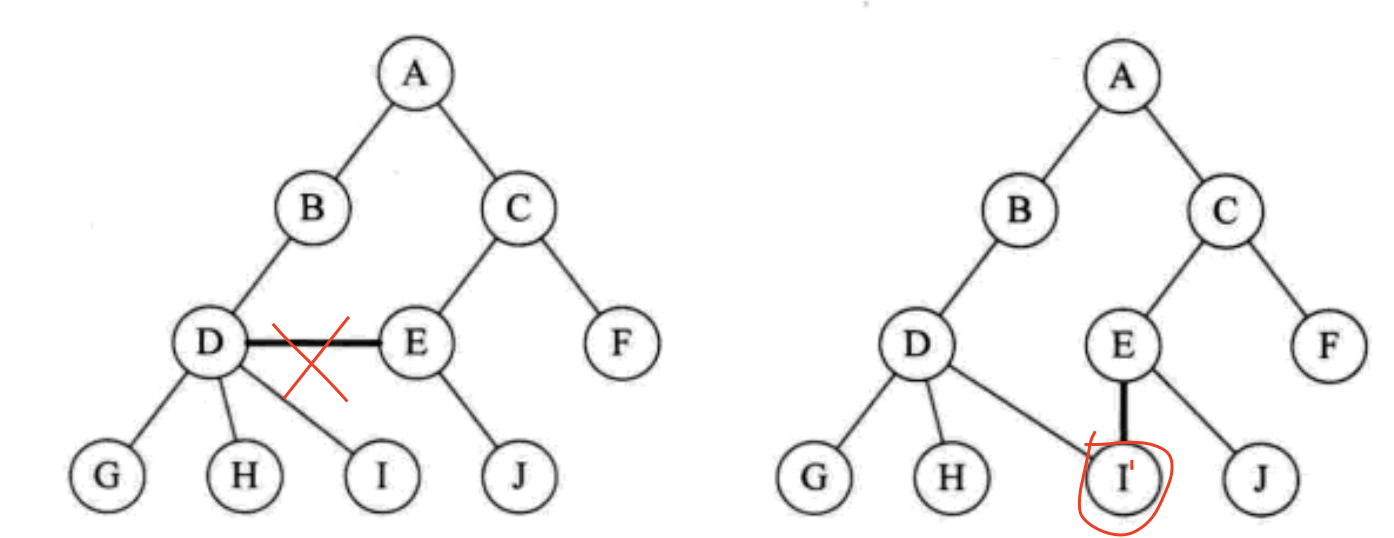
3.4.3 clue binary tree

^: indicates null pointers. The binary tree in the figure has many null pointers. It is found that these spaces are not utilized. In fact, this is not a good phenomenon and should be used reasonably
First, let's see how many null pointers there are?
For a binary tree with n nodes, there are 2n pointers, and the binary tree with n nodes has a total of n-1 branch lines, that is, there are 2n-(n-1)=n+1 null pointer fields. Corresponding to the problem, there is a waste of 11 null pointers
On the other hand, we traverse the binary tree in the middle order to get HDIBJEAFCG. For such a character sequence, we know that the precursor of J is B and the successor is E, that is to say, we can know the precursor and successor of any node by traversing the binary tree in the middle order
Problem: the law found above is based on the traversal. On the binary list, we only know the address of each left and right child, but do not know who the successor is and who the successor is. If we want to know, we must traverse again
Solution
We create the predecessor and successor when traversing
We call this precursor and subsequent pointers clues, the binary linked list with clues is called clue linked list, and the corresponding binary tree is called threaded binary tree
We traverse the binary tree in middle order, and change the rchild of all null pointers to point to its subsequent nodes. Therefore, we can know that the successor of H is D(1) through the pointer ⃣ I is followed by B(2) ⃣ J is followed by E(3) ⃣ ️)(E.next = A(4 ⃣ ️), F.next = C(5 ⃣ ️), G.next = null(6 ⃣ At this time, a total of 6 null pointers are used
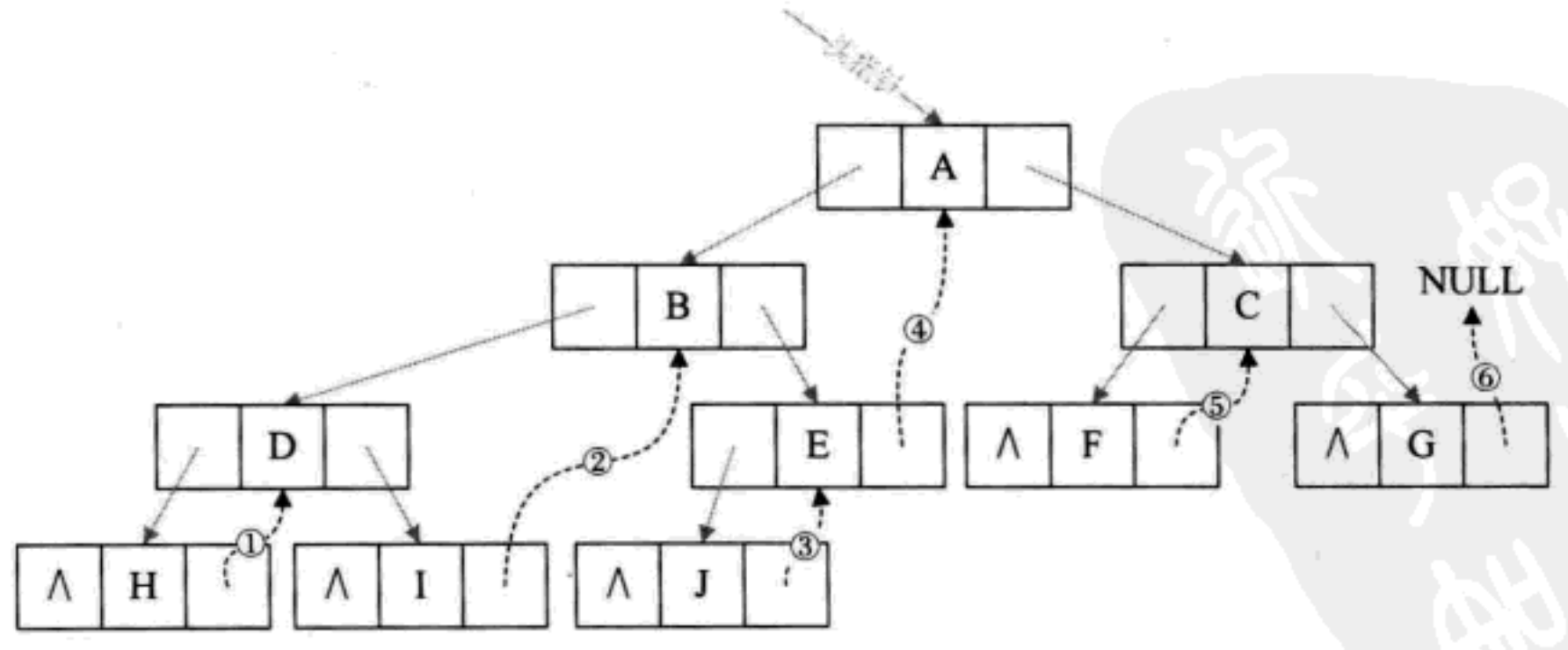
Look at the figure again. Change the lchild in all empty finger needle fields in this binary tree to point to the precursor of the current node. Therefore, the precursor of H is NULL(1) ⃣ The precursor of I is D(2) ⃣ ️)[J.prev = B(3 ⃣ ️), F.prev = A(4 ⃣ ️), G.prev = C(5 ⃣ ]. A total of 5 null pointers are used. After the right subtree above is used, a total of 11 null pointers are used
The solid and hollow arrows are the precursor prev, and the dotted solid arrows are the successor next
It is easier to see that the clue binary tree is equivalent to turning a binary tree into a two-way linked list, which is convenient for us to insert and delete nodes and find a node. Therefore, we traverse the binary tree in a certain order to turn it into a clue binary tree

Binary search tree and bidirectional linked list
OJ topic exercise

Java: Building Code
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
private TreeNode prev = null;// 1. Used to record the precursor node
private void ConvertChild(TreeNode root){
if(root == null){
return;
}else{
// 2. Nature of radical binary search tree: medium order traversal is an ordered result
ConvertChild(root.left);
/*
3.Establish forward and backward pointing
The left subtree of a node is the precursor and the right subtree is the successor
For the leftmost leaf node 4, which has no left and right subtrees, special consideration should be given: the right subtree of the reserved precursor node points to the node of the current function call [4.right = 6], but in this case, it is also necessary to judge whether it is null, otherwise the null pointer will be abnormal
4.left = null
null.right = 4;Null pointer exception
null = 4;
After adding if judgment:
4.left = null;
null = 4;
Program return returns to the 6-node function
6.left = 4;
4.right = 6;
4 = 6;
*/
root.left = prev;// At the end of the first recursion, the node returned to root is 4
if(prev != null){
prev.right = root;
}
prev = root;
ConvertChild(root.right);
}
}
public TreeNode Convert(TreeNode pRootOfTree) {
if(pRootOfTree == null){
return null;
}else{
ConvertChild(pRootOfTree);
while(pRootOfTree.left != null){
pRootOfTree = pRootOfTree.left;
}
return pRootOfTree;
}
}
}
When defining the node class, the Java language only needs: data field val, left subtree and right subtree. When implementing the two-way linked list, an additional prev node is required to store the precursor [left subtree] of the current node

C: Clue binary tree structure
lchild: left subtree, rchild: right subtree
For C language, how do we know whether the lchild of a node points to its left child or to its precursor? Does rchild point to the right child or the successor?
For example, the lchild of node E points to its left subtree J, while the rchild points to its successor A. obviously, we need a distinguishing flag to determine whether the lchild points to the left child or the precursor, and whether the rchild points to the right child or the successor. Therefore, we add two flag fields ltag and rtag to each node, Note that ltag and rtag only store Boolean variables of 0 and 1, which occupy less memory space than pointer variables such as lchild and rchild
| lchild | ltag | data | rtag | rchild |
|---|
- ltag == 0 points to the left child of the node, and 1 points to the successor of the node
- rtag == 0 points to the right child of the node, and 1 points to the successor of the node

typedef int DataType;// data type
typedef enum {
Link,//Link == 0 means that you only want to do it, and there are subtree pointers
Thread, //Thread == 1 indicates that only the precursor or successor clues are wanted
} PointerTag;
typedef struct BiThrNode {// Binary tree storage node structure
DataType data;// Data domain
struct BiThrNode *lchild, *rchild;// Left and right subtree
PointerTag LTag;// Left sign
PointerTag RTag;// Right sign
}BiThrNode, *BiThrTree;
So how do we implement it after we understand the structure of C language and the principle of clue binary tree?
Referring to the implementation of the previous Java code, we find that the law is nothing more than how to process the data from the left root to the right. It is nothing more than how to process the data from the middle root
BiThrNode *prev;// Global variable, always pointing to the node just accessed
void InThreading(BiThrNode *pb) {
if (pb) {
/*
* Middle order traversal cued binary tree recursive function
*/
// 1. Left
InThreading(pb->lchild);
/*
* 2.Establish contact with the middle part
* Because the first element after the middle order traversal is the head node of the linked list, the node whose left node is empty should be selected as the chain header node
*
* Precursor analysis:
* if(!pb->lchild): Indicates that if the left subtree domain of a node is empty, because its predecessor node has just accessed it
* Assigned to prev, so you can assign prev to Pb - > lchild, and modify Pb - > LTAG = thread. The cueing of the precursor node is completed
* Follow up analysis:
* At this time, the successor of the pb node has not been accessed yet. It can only be judged by the right subtree rchild of its predecessor node prev:
* if(!prev-rchild)If it is empty, pb is the successor of prev, so prev thread, prev - > rchild = pb completes the cueing of the successor node
* After completing the judgment of the precursor and subsequent, the pb is given to prev for the next traversal
*/
if (!pb->lchild) {// If there is no left child
pb->LTag = Thread;// Precursor clue
pb->lchild = prev;// The left child's pointer points to the front drive
}
if (!prev->rchild) {// If there is no right child
prev->LTag = Thread;// Subsequent clues
prev->lchild = pb;// The right child pointer points to the successor
}
prev = pb;
// 3. Right
InThreading(pb->rchild);
}
}