Code Link:

1 PCA brief introduction

Principal Component Analysis (PCA) principal component analysis (PCA) algorithm has a strong application in image recognition and dimension reduction of high-dimensional data. The PCA algorithm can transform the original data linearly by calculating and choosing eigenvectors with larger eigenvalues, which can not only remove useless noise, but also reduce the amount of computation. .

2 Algorithmic Processes

2.1 All samples were centralized.

The average value of the corresponding features of all samples is subtracted from the different features of each sample in the data set, and the average value of the data on the different features processed is 0. The advantage of this method is that it can reduce the difference between features, make different features have the same scale, and make different features have the same influence on parameters.

 

 

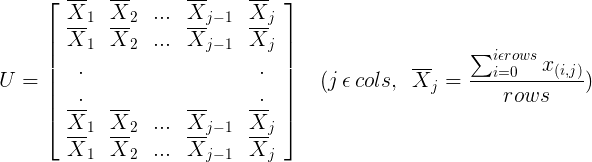
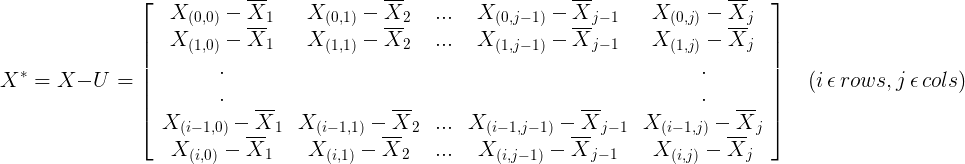
2.2 Calculate the covariance matrix of samples (each column represents a feature and each row represents a sample)

2.2.1 Calculate the mean of each column of the sample matrix

 

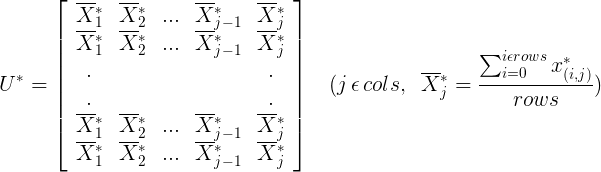
2.2.2 Sample Matrix Subtracts the Mean of Corresponding Sequences from Each Sample

 

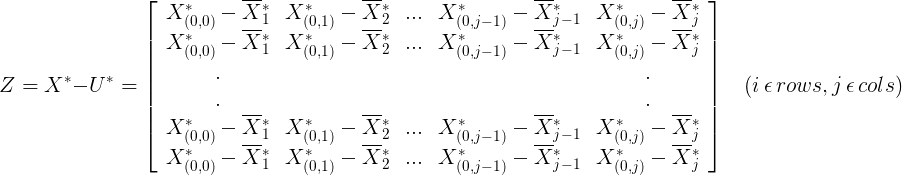
2.2.3 obtain the covariance matrix (m is the total number of samples) by the following formula

 

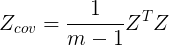
2.3 Eigenvalue decomposition of covariance matrix is performed to obtain eigenvalues and eigenvectors.

2.4 The projection matrix W is constructed by extracting the eigenvectors corresponding to the largest k eigenvalues.

2.5 For each sample in the sample set, the projection matrix W is multiplied to obtain dimensionality reduction data.

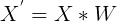
3 Python code example

#encoding:GBK
"""
Created on 2019/09/23 16:19:11
@author: Sirius_xuan
"""
'''
//Image Dimension Reduction and Reconstruction Based on PCA
'''

import numpy as np
import cv2 as cv

#Data Centralization
def Z_centered(dataMat):
	rows,cols=dataMat.shape
	meanVal = np.mean(dataMat, axis=0)  # Find the mean by column, that is to say, the mean of each feature.
	meanVal = np.tile(meanVal,(rows,1))
	newdata = dataMat-meanVal
	return newdata, meanVal

#covariance matrix
def Cov(dataMat):
	meanVal = np.mean(data,0) #Compress rows, return 1*cols matrix, average columns
	meanVal = np.tile(meanVal, (rows,1)) #Returns the mean matrix of rows rows
	Z = dataMat - meanVal
	Zcov = (1/(rows-1))*Z.T * Z
	return Zcov
	
#Minimize the loss caused by dimensionality reduction and determine k
def Percentage2n(eigVals, percentage):
	sortArray = np.sort(eigVals)  # Ascending order
	sortArray = sortArray[-1::-1]  # Reversal, i.e. descending order
	arraySum = sum(sortArray)
	tmpSum = 0
	num = 0
	for i in sortArray:
		tmpSum += i
		num += 1
		if tmpSum >= arraySum * percentage:
			return num
	
#Get the largest k eigenvalues and eigenvectors
def EigDV(covMat, p):
	D, V = np.linalg.eig(covMat) # Get eigenvalues and eigenvectors
	k = Percentage2n(D, p) # Determine k value
	print("Retain 99%Information, the number of features after dimensionality reduction:"+str(k)+"\n")
	eigenvalue = np.argsort(D)
	K_eigenValue = eigenvalue[-1:-(k+1):-1]
	K_eigenVector = V[:,K_eigenValue]
	return K_eigenValue, K_eigenVector
	
#Data after dimensionality reduction
def getlowDataMat(DataMat, K_eigenVector):
	return DataMat * K_eigenVector

#Refactoring data
def Reconstruction(lowDataMat, K_eigenVector, meanVal):
	reconDataMat = lowDataMat * K_eigenVector.T + meanVal
	return reconDataMat

#PCA algorithm
def PCA(data, p):
	dataMat = np.float32(np.mat(data))
	#Data Centralization
	dataMat, meanVal = Z_centered(dataMat)
	#Computation of covariance matrix
		#covMat = Cov(dataMat)
	covMat = np.cov(dataMat, rowvar=0)
	#Get the largest k eigenvalues and eigenvectors
	D, V = EigDV(covMat, p)
	#Data after dimensionality reduction
	lowDataMat = getlowDataMat(dataMat, V)
	#Refactoring data
	reconDataMat = Reconstruction(lowDataMat, V, meanVal)
	return reconDataMat

def main():
	imagePath = 'D:/desktop/banana.jpg'
	image = cv.imread(imagePath)
	image=cv.cvtColor(image,cv.COLOR_BGR2GRAY)
	rows,cols=image.shape
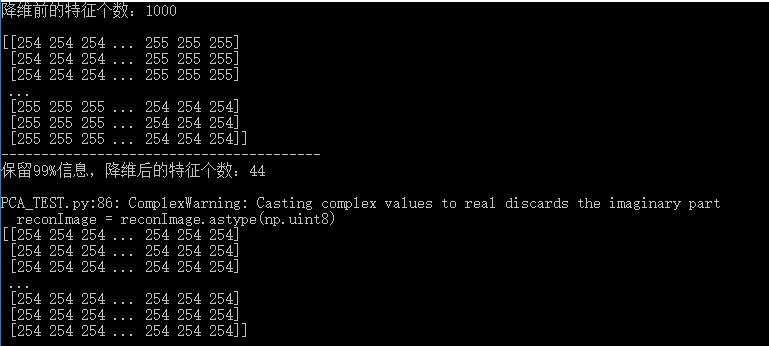
	print("The number of features before dimensionality reduction:"+str(cols)+"\n")
	print(image)
	print('----------------------------------------')
	reconImage = PCA(image, 0.99)
	reconImage = reconImage.astype(np.uint8)
	print(reconImage)
	cv.imshow('test',reconImage)
	cv.waitKey(0)
	cv.destroyAllWindows()


if __name__=='__main__':
	main()

	
	
	


	
	

 

4 Results

Before reconstruction

After reconstruction

5 Summary

It is not difficult to find that with 99% of the information retained, the dimension is reduced from 1000 to 44, which greatly reduces the computational complexity of image classification. The features before and after reconstruction are still obvious. Readers can also adjust percentage parameters themselves to experience the effect of PCA.

 

PS: Like readers, you are welcome to comment at any time, if you feel benefited, give the blogger a compliment!!