Image of JZ18 binary tree

(simple)

subject

describe
Operate the given binary tree and transform it into a mirror of the source binary tree.
For example: source binary tree
    8
  /     \
6     10
/ \     /   \
5 7   9  11
Mirror binary tree
     8
  /      \
10     6
/ \      /  \
11 9  7 5

Example
Input:
{8,6,10,5,7,9,11}
Return value:
{8,10,6,11,9,7,5}

thinking

Method 1:

According to the description of the topic, the operation of converting the tree into a mirror binary tree is to exchange the positions of two brother nodes at each layer of the tree structure (in fact, this topic does not strictly limit the scope to a complete binary tree, nor explain how to deal with such situations. Therefore, we can do it according to a complete binary tree). Therefore, the operation is carried out layer by layer. Therefore, We can complete the operation of a pair of sibling nodes in each layer (of course, there may be one node without sibling nodes, that is, the corresponding other node is null) in the loop. Therefore, we can use the breadth first traversal of the binary tree to complete it, that is, with the help of a queue, we can realize the temporary storage of the nodes in each layer while cycling, In each cycle, one node is out of the queue, and the left and right child nodes are operated to exchange until there are no more nodes in the queue.

(supplement: breadth first traversal is also often used in graph data structures. If you need it, please refer to the previous article:
Java implementation [creation and traversal of adjacency matrix and adjacency table (DFS, BFS)] + diagram + complete code
)

Method 2:

This problem can also be realized by recursive traversal of the tree (pre, middle and post order traversal), and the mirror operation is carried out at the same time.

(supplement: if you need the knowledge of this part, please refer to the previous article: Data structure [complete code] (C language implements [binary tree] creation, recursive traversal (pre order, middle order, post order), and non recursive pre order traversal))

realization

class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;
    public TreeNode(int val) {
        this.val = val;
    }
}

public class Solution {
	//Method 1
    public TreeNode Mirror (TreeNode pRoot) {
        if (pRoot == null) {
            return null;
        }

        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.add(pRoot);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
            TreeNode tempNode = node.left;
            node.left = node.right;
            node.right = tempNode;
        }
        return pRoot;
    }


	//Method 2
	
	public TreeNode Mirror_inOrder(TreeNode root) {
	  if (root == null)
	        return null;
	    Mirror_inOrder(root.left);
	    //Child node switching
	    TreeNode temp = root.left;
	    root.left = root.right;
	    root.right = temp;
	    //The above has been exchanged. Here is root Right to become root left
	    Mirror_inOrder(root.left);
	    return root;
	}
	
	public TreeNode Mirror_postOrder(TreeNode root) {
	    if (root == null)
	        return null;
	    TreeNode left = Mirror_postOrder(root.left);
	    TreeNode right = Mirror_postOrder(root.right);
	    root.left = right;
	    root.right = left;
	    return root;
	}
}

The test method is not customized here, and the test mechanism on the test platform is directly used.

JZ20 stack containing min function

(simple)

subject

describe
To define the data structure of the stack, please implement a min function in this type that can get the smallest element in the stack, and the time complexity of calling min function, push function and pop function is O(1)
push(value): push value into the stack
pop(): pop up stack top element
top(): get stack top element
min(): get the smallest element in the stack

Example:
Input: [PSH-1 "," PSH2 "," MIN "," TOP "," POP "," PSH1 "," TOP "," MIN "]
Output: - 1,2,1, - 1
Resolution:
"PSH-1" means to push - 1 into the stack, and the element in the stack is - 1
"PSH2" means to push 2 into the stack, and the elements in the stack are 2, - 1
"MIN" means to get the smallest element in the stack = = > Return - 1
"TOP" means to get the stack TOP element = = > return 2
"POP" means POP the top element of the stack, POP 2, and the element in the stack is - 1
"PSH-1" means to push 1 into the stack, and the elements in the stack are 1, - 1
"TOP" means to get the stack TOP element = = > Return 1
"MIN" means to get the smallest element in the stack = = > Return - 1

Example
Input:
["PSH-1","PSH2","MIN","TOP","POP","PSH1","TOP","MIN"]
Return value:
-1,2,1,-1

thinking

My first idea about this problem is to use a stack to store data and do basic operations of entering and exiting the stack. At the same time, I set two variables to store the current minimum value and the top value. However, when I wrote about the logic in the red box area, I suddenly realized that if the node exiting the stack is the minimum value node, how to deal with the subsequent minimum node value will be cumbersome, In addition, a new data structure needs to be set for storage. For example, a linked list is added, which is used to store the current minimum node value each time. Each time it is out of the stack, if the current out of the stack node is the minimum node, the last node in the linked list is deleted at the same time, and the last node of the newly modified linked list is assigned to the variable of the current minimum value.

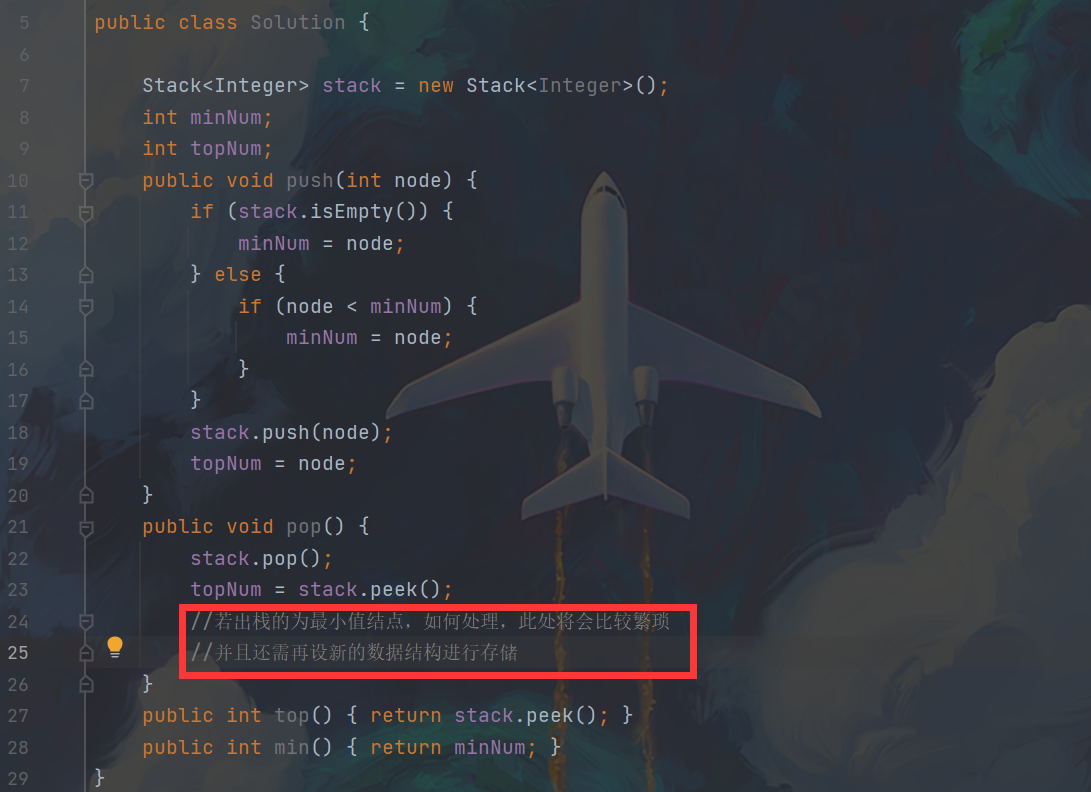
But I always feel so troublesome, and it seems that it is not the purpose of this problem - to investigate the stack, because my idea has introduced the data structure of linked list (of course, it is OK to store it in array), and it may also lead to the situation that the time complexity exceeds the requirements of the problem. Therefore, I am very uncertain whether the idea of solving this problem is the same as I think, I read the solution. Sure enough, the official gave a very clever method to abstract the two arrays into two stacks to solve the problem - first, a main stack normal is needed for the normal operation of the stack, and then an auxiliary stack minval is needed to obtain the minimum value. Whenever a new data is put into the stack, the data is put into the main stack, If this data is smaller than the top data value in the auxiliary stack, it will also be put into the auxiliary stack. Otherwise, the auxiliary stack will press the value of its top stack again, that is, the minimum value in the current stack. For the out of stack operation, when the main stack produces one data, the auxiliary stack should also produce one data, which ensures the consistency of the minimum values of the two stacks. In addition, It is also necessary to consider the judgment and inspection of some critical problems. Specifically, add logic to the code. The schematic operation of the idea is as follows.

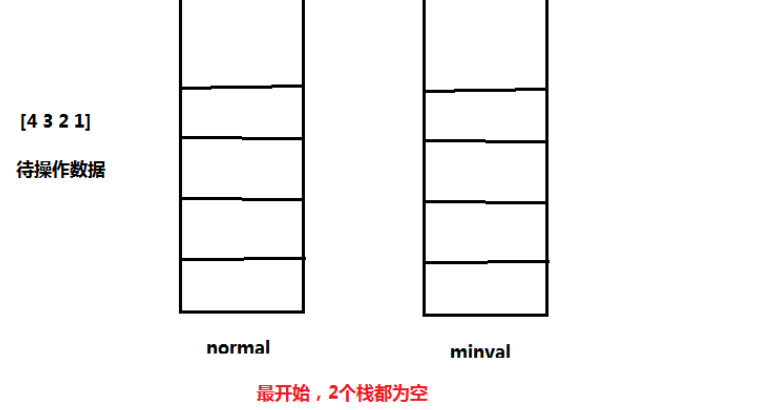
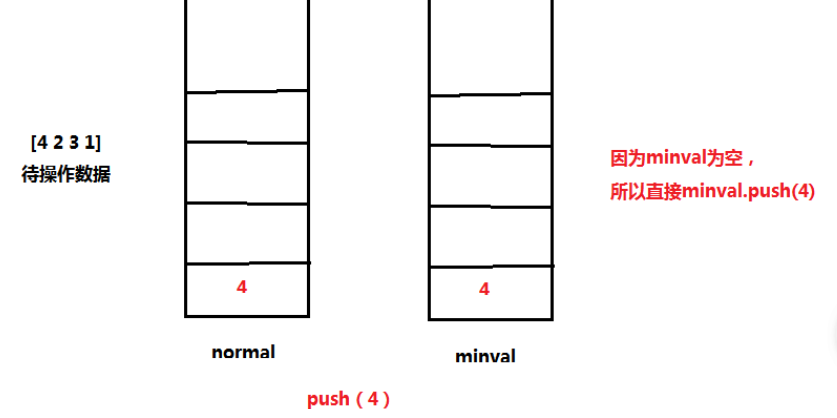
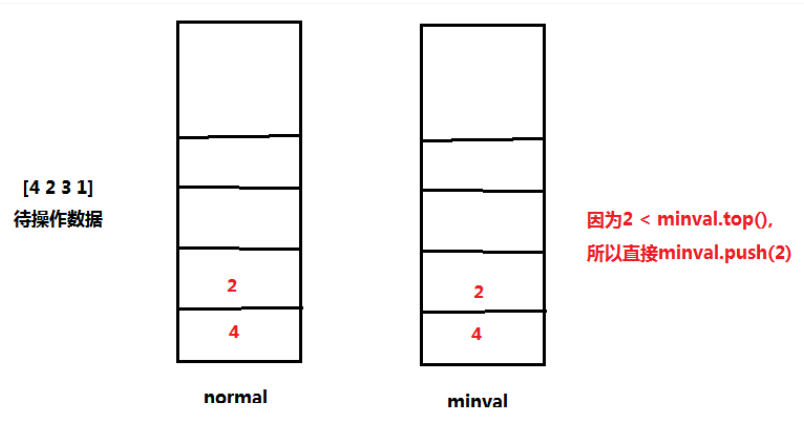
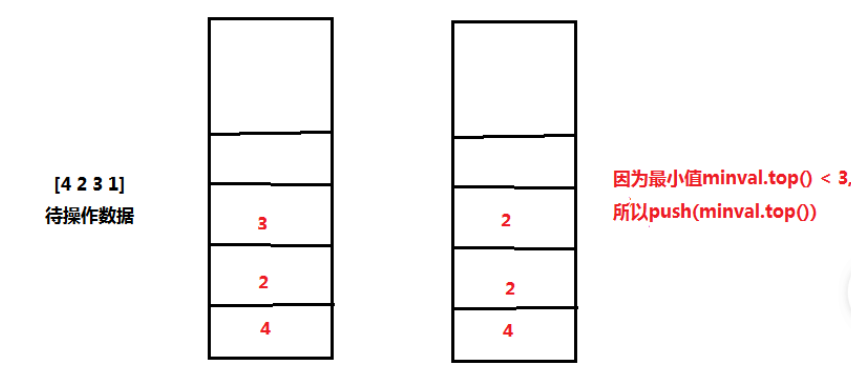
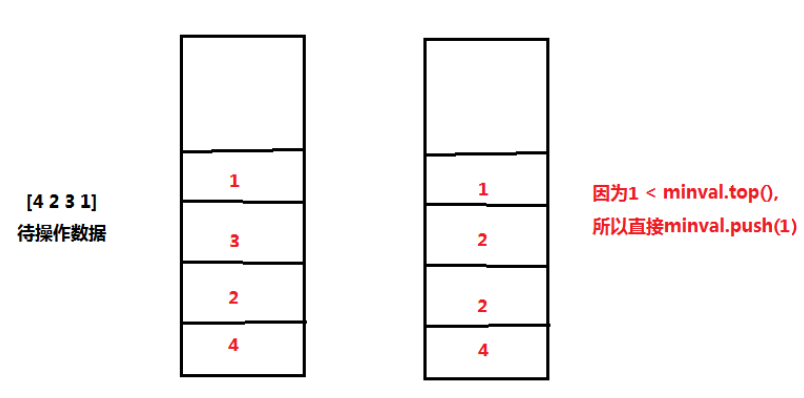
realization

public class Solution {

    int[] stack = new int[100];
    int top = -1;
    int[] stackMin = new int[100];
    int topMin = -1;

    public void push(int node) {
        if (top > stack.length - 1) {
            //Stack full
            throw new ArrayIndexOutOfBoundsException("The stack is full. No new data can be put into the stack");
        }
        stack[++top] = node;
        if (topMin == -1) {
            stackMin[++topMin] = node;
        } else {
            if (stackMin[topMin] < node) {
                int temp = stackMin[topMin];
                stackMin[++topMin] = temp;
            } else {
                stackMin[++topMin] = node;
            }
        }
    }
    public void pop() {
        stack[top--] = 0;
        stackMin[topMin--] = 0;
    }
    public int top() {
        return stack[top];
    }
    public int min() {
        return stackMin[topMin];
    }
}