Image processing_ Gray transformation_ histogram

Histogram Equalization

If the gray distribution of the image is uneven, its gray distribution is concentrated in a narrow range, so that the details of the image are not clear enough and the contrast is low. Histogram equalization and histogram specification are usually used to open the gray range of the image or make the gray evenly distributed, so as to increase the contrast and make the image details clear, so as to achieve the purpose of enhancement. Histogram equalization, nonlinear stretching of the image, redistribution of the gray value of the image, so that the gray value of the image is roughly equal in a certain range. In this way, the contrast of the peak part in the middle of the original histogram is enhanced, while the contrast of the valley bottom part on both sides is reduced, and the histogram of the output image is a relatively flat histogram.

Equalization algorithm

Histogram equalization is actually a gray transformation process. The current gray distribution is transformed into an image with wider range and more uniform gray distribution through a transformation function. That is, the histogram of the original image is modified to be roughly evenly distributed in the whole gray interval, so the dynamic range of the image is expanded and the contrast of the image is enhanced. Generally, the transformation function selected for equalization is the cumulative probability of gray level. The steps of histogram equalization algorithm are as follows:

1. Calculate the gray histogram P (S_k) = n of the original image_ Kn, where n is the total number of pixels, n_k is gray level s_ Number of pixels of K
2. Calculate the cumulative histogram of the original image CDF(S_k)=\sum_{i=0}^kn_in=\sum_{i=0}^kPs(Si)

D_j=L ⋅ CDF(S_i), where D_j is the pixel of the target image, CDF(S_i) is the cumulative distribution of the gray level of the source image I, and L is the maximum gray level in the image (the gray level image is 255). This method is directly applied to obtain the gray histogram of the image

1. Normalize the gray histogram and calculate the cumulative probability of gray; Create a lookup table for grayscale changes

The look-up table is applied to transform the original image into a gray-scale balanced image

In the process of equalization, two conditions must be guaranteed

1. No matter how the pixels are mapped, we must ensure that the original size relationship remains unchanged. The brighter areas are still brighter, and the darker areas are still darker, but the contrast increases, and the light and shade must not be reversed;

1. If it is an eight bit image, the value range of the pixel mapping function should be between 0 and 255 and cannot exceed the limit.

Combining the above two conditions, the cumulative distribution function is a good choice, because the cumulative distribution function is a monotonic increasing function (control size relationship) and the value range is 0 to 1 (control out of bounds problem), so the cumulative distribution function is used in histogram equalization.

Cumulative distribution function

Cumulative distribution function has some good properties, so how to use cumulative distribution function to make histogram equalization? Comparing the probability distribution function with the cumulative distribution function, the two-dimensional image of the former is uneven, and the latter is monotonically increasing. In the process of histogram equalization, the mapping method is

S_k = \sum_{j=0}^k\frac{n_j}{n} . k=0,1...,L-1

N is the sum of graph pixels, n_k is the number of pixels of the current gray level, and L is the total number of gray levels in the image

The operation steps are:

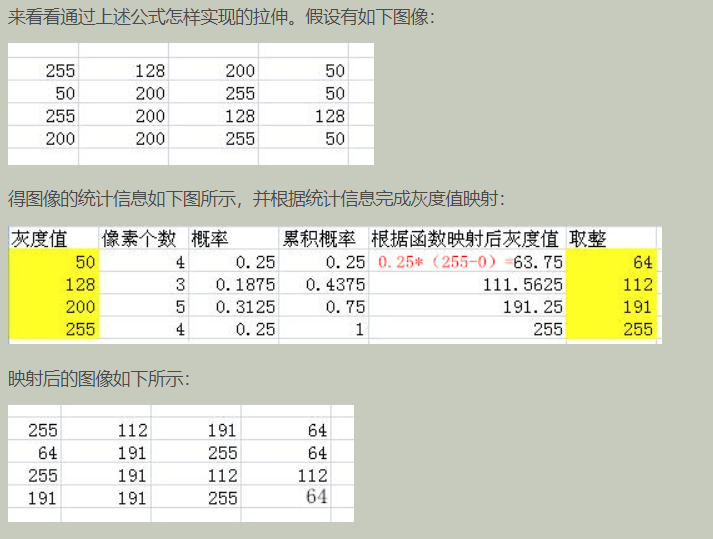
Histogram specification

Histogram specification is to transform the original image so that the histogram of the transformed image is the same as that specified by us.

The specific steps are as follows:

1. Firstly, histogram equalization is performed on the original image to obtain each pixel s and cumulative distribution T(s);
2. Calculate the cumulative integral distribution G(Z) according to the required specified histogram;
3. Obviously, if there is a value of 0 in the cumulative histogram, the pixel value will not be allocated, because 0 multiplied by 255 is still zero.
4. For each T (s) (assuming that its pixel value is ss), find the G (z) value with the smallest difference in G (z) (assuming that the corresponding pixel value is zz), and then transform ss into ZZ after specification.

The histogram specification process is shown in the figure below:

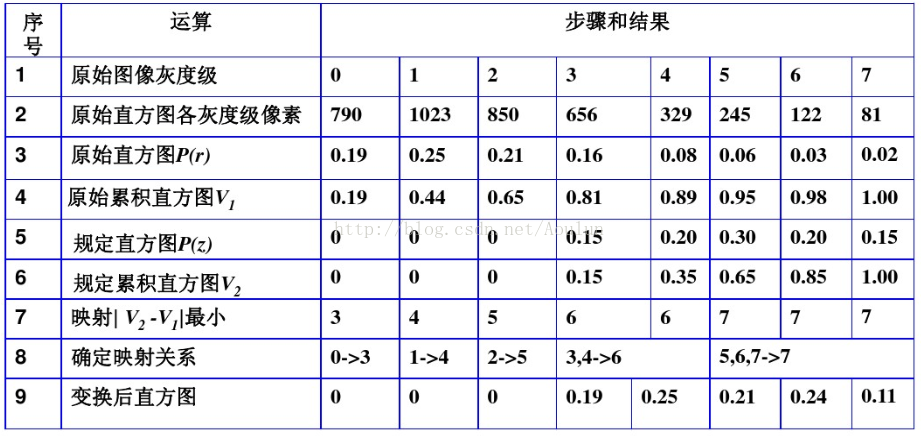
1. Calculate the cumulative histogram of the original image
2. Calculate the cumulative histogram of the specified histogram
3. Calculate the absolute value of the difference between the two cumulative histograms
4. The gray level mapping is established according to the cumulative histogram difference

Local histogram processing & histogram statistics

Opencv code

Gray histogram equalization

// HistogramGrayEqualizeHist.cpp: defines the entry point for the console application.
//

#include "stdafx.h"

#include <iostream>
#include <opencv2/core/core.hpp>   //cvGetSize  cvCreateImage
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/opencv.hpp>  //cvResize cvInitMatHeader cvGetMinMaxHistValue cvCvtColor
#include <opencv2/imgproc/imgproc.hpp>

#ifdef _DEBUG
#pragma comment(lib, "opencv_core244d")
#pragma comment(lib, "opencv_highgui244d")
#pragma comment(lib, "opencv_imgproc244d")  //cvResize
#else
#pragma comment(lib, "opencv_core244d")
#pragma comment(lib, "opencv_highgui244d")
#pragma comment(lib, "opencv_imgproc244d")  //cvResize
#endif
#define cvQueryHistValue_1D(hist,idx0) ((float)cvGetReal1D( (hist)->bins, (idx0)))

using namespace std;  
#pragma comment(linker, "/subsystem:\"windows\" /entry:\"mainCRTStartup\"")  
void FillWhite(IplImage *pImage)  
{  
    cvRectangle(pImage, cvPoint(0, 0), cvPoint(pImage->width, pImage->height), CV_RGB(255, 255, 255), CV_FILLED);  
}  
// Creates a histogram of a grayscale image  
CvHistogram* CreateGrayImageHist(IplImage **ppImage)  
{  
    int nHistSize = 256;  
    float fRange[] = {0, 255};  //Range of gray levels  
    float *pfRanges[] = {fRange};  
    CvHistogram *pcvHistogram = cvCreateHist(1, &nHistSize, CV_HIST_ARRAY, pfRanges);  
    cvCalcHist(ppImage, pcvHistogram);  
    return pcvHistogram;  
}  
// Create histogram image from histogram  
IplImage* CreateHisogramImage(int nImageWidth, int nScale, int nImageHeight, CvHistogram *pcvHistogram)  
{  
    IplImage *pHistImage = cvCreateImage(cvSize(nImageWidth * nScale, nImageHeight), IPL_DEPTH_8U, 1);  
    FillWhite(pHistImage);  
  
    //Maximum square in statistical histogram  
    float fMaxHistValue = 0;  
    cvGetMinMaxHistValue(pcvHistogram, NULL, &fMaxHistValue, NULL, NULL);  
  
    //Draw the values of each straight square into the figure respectively  
    int i;  
    for(i = 0; i < nImageWidth; i++)  
    {  
        float fHistValue = cvQueryHistValue_1D(pcvHistogram, i); //The size of a straight square with pixel i  
        int nRealHeight = cvRound((fHistValue / fMaxHistValue) * nImageHeight);  //Height to draw  
        cvRectangle(pHistImage,  
            cvPoint(i * nScale, nImageHeight - 1),  
            cvPoint((i + 1) * nScale - 1, nImageHeight - nRealHeight),  
            cvScalar(i, 0, 0, 0),   
            CV_FILLED  
            );   
    }  
    return pHistImage;  
}  
int main( int argc, char** argv )  
{   
    const char *pstrWindowsSrcTitle = "Original drawing";  
    const char *pstrWindowsGrayTitle = "Grayscale image";  
    const char *pstrWindowsHistTitle = "histogram";  
    const char *pstrWindowsGrayEqualizeTitle = "Grayscale image-After equalization";  
    const char *pstrWindowsHistEqualizeTitle = "histogram-After equalization";  
    
    // Load original drawing from file  
    // IplImage *pSrcImage = cvLoadImage("./images/yangmi.jpg", CV_LOAD_IMAGE_UNCHANGED);  
    IplImage *pSrcImage = cvLoadImage("./images/beauty.png", CV_LOAD_IMAGE_UNCHANGED);  
    IplImage *pGrayImage = cvCreateImage(cvGetSize(pSrcImage), IPL_DEPTH_8U, 1);  
    IplImage *pGrayEqualizeImage = cvCreateImage(cvGetSize(pSrcImage), IPL_DEPTH_8U, 1);  
    
    // Grayscale image  
    cvCvtColor(pSrcImage, pGrayImage, CV_BGR2GRAY);  
    // Histogram image data  
    int nHistImageWidth = 255;  
    int nHistImageHeight = 150;   
    int nScale = 2;  
  
    // Gray histogram and histogram image  
    CvHistogram *pcvHistogram = CreateGrayImageHist(&pGrayImage);  
    IplImage *pHistImage = CreateHisogramImage(nHistImageWidth, nScale, nHistImageHeight, pcvHistogram);  
  
    // Equalization 
    //Function function: histogram equalization, which can normalize image brightness and enhance contrast
    //The first parameter represents the input image, which must be a grayscale image (8-bit, single channel image)
    //The second parameter represents the output image
    //This function uses the following rules to equalize the histogram of the input image:
        //1: Calculate the histogram H of the input image.
        //2: The histogram is normalized, so the sum of straight squares is 255.
        //3: Calculate the histogram integral, H '(I) = sum (H (J)) (0 < = J < = I).
        //4: H 'is used as the query table: dst(x, y) = H'(src(x, y)) for image transformation.
    cvEqualizeHist(pGrayImage, pGrayEqualizeImage);  
  
    // Gray histogram and histogram image after equalization  
    CvHistogram *pcvHistogramEqualize = CreateGrayImageHist(&pGrayEqualizeImage);       
    IplImage *pHistEqualizeImage = CreateHisogramImage(nHistImageWidth, nScale, nHistImageHeight, pcvHistogramEqualize);  
  
    // display  
    cvNamedWindow(pstrWindowsSrcTitle); 
    cvNamedWindow(pstrWindowsGrayTitle); 
    cvNamedWindow(pstrWindowsGrayEqualizeTitle); 
    cvNamedWindow(pstrWindowsHistTitle); 
    cvNamedWindow(pstrWindowsHistEqualizeTitle); 
    cvShowImage(pstrWindowsSrcTitle,pSrcImage);
    cvShowImage(pstrWindowsGrayTitle,pGrayImage);
    cvShowImage(pstrWindowsGrayEqualizeTitle,pGrayEqualizeImage);
    cvShowImage(pstrWindowsHistTitle,pHistImage);
    cvShowImage(pstrWindowsHistEqualizeTitle,pHistEqualizeImage);
    cvWaitKey(0);  
    //Recycle resource code  
    cvDestroyWindow(pstrWindowsSrcTitle);
    cvDestroyWindow(pstrWindowsGrayTitle);
    cvDestroyWindow(pstrWindowsGrayEqualizeTitle);
    cvDestroyWindow(pstrWindowsHistTitle);
    cvDestroyWindow(pstrWindowsHistEqualizeTitle);
    cvReleaseImage(&pSrcImage);
    cvReleaseImage(&pGrayImage);
    cvReleaseImage(&pGrayEqualizeImage);
    cvReleaseImage(&pHistImage);
    cvReleaseImage(&pHistEqualizeImage);
    return 0;  
}

Histogram specification

void hist_specify(const Mat &src, const Mat &dst,Mat &result)
{
    Histogram1D hist1D;
    MatND src_hist = hist1D.getHistogram(src);
    MatND dst_hist = hist1D.getHistogram(dst);

    float src_cdf[256] = { 0 };
    float dst_cdf[256] = { 0 };

    // The size of the source image is different from that of the target image, so the histogram obtained should be normalized
    src_hist /= (src.rows * src.cols);
    dst_hist /= (dst.rows * dst.cols);

    // Calculate the cumulative probability of the original histogram and the specified histogram
    for (int i = 0; i < 256; i++)
    {
        if (i == 0)
        {
            src_cdf[i] = src_hist.at<float>(i);
            dst_cdf[i] = dst_hist.at<float>(i);
        }
        else
        {
            src_cdf[i] = src_cdf[i - 1] + src_hist.at<float>(i);
            dst_cdf[i] = dst_cdf[i - 1] + dst_hist.at<float>(i);
        }
    }

    // Difference of cumulative probability
    float diff_cdf[256][256];
    for (int i = 0; i < 256; i++)
        for (int j = 0; j < 256; j++)
            diff_cdf[i][j] = fabs(src_cdf[i] - dst_cdf[j]);

    // Build gray level mapping table
    Mat lut(1, 256, CV_8U);
    for (int i = 0; i < 256; i++)
    {
        // Find mapped grayscale with source grayscale I
        //The specified gray scale with the smallest cumulative probability difference between and I
        float min = diff_cdf[i][0];
        int index = 0;
        for (int j = 1; j < 256; j++)
        {
            if (min > diff_cdf[i][j])
            {
                min = diff_cdf[i][j];
                index = j;
            }
        }
        lut.at<uchar>(i) = static_cast<uchar>(index);
    }

    // Apply look-up table to specify histogram
    LUT(src, lut, result);
}