In this article, you will learn how self encoders work and why they are used for medical image denoising.
Correct understanding of image information is very important in medicine and other fields. Denoising can focus on cleaning up old scanned images or contribute to feature selection in cancer biology. The presence of noise may confuse the identification and analysis of diseases, resulting in unnecessary death. Therefore, medical image denoising is an essential preprocessing technology.
The so-called self encoder technology has proved to be very useful for image denoising.
The self encoder is composed of two interconnected artificial neural networks: encoder model and decoder model. The goal of the automatic encoder is to find a method to encode the input image into a compressed format (also known as potential space), so that the decoded image version is as close to the input image as possible.
How does Autoencoders work
The network provides the original images x, as well as their noisy versions x~. The network attempts to reconstruct its output X 'as close to the original image x as possible. By doing so, it learned how to denoise the image.
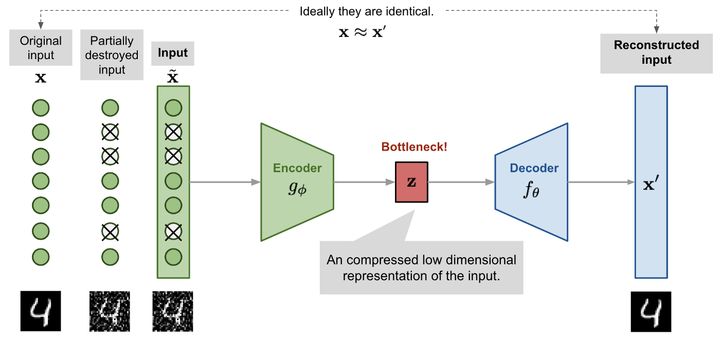
As shown in the figure, the encoder model converts the input into a small and dense representation. The decoder model can be regarded as a generation model, which can generate specific features.
Encoder and decoder networks are usually trained as a whole. The loss function determines the difference between the output x 'created by the network and the original input x.
By doing so, the encoder learns to retain as much relevant information as possible in a limited potential space and skillfully discard irrelevant parts, such as noise. The decoder learns to take compressed potential information and reconstruct it into a completely error free input.
How to realize automatic encoder
Let's implement an automatic encoder to denoise handwritten digits. The input is a 28x28 grayscale image to construct a 784 element vector.
The encoder network is a dense layer composed of 64 neurons. Therefore, the potential space will have dimension 64. A ReLu activation function is attached to each neuron in this layer. Whether the neuron should be activated is determined according to whether the input of each neuron is related to the prediction of the self encoder. The activation function also helps to regularize the output of each neuron into a range between 1 and 0.
The decoder network is a single dense layer composed of 784 neurons, corresponding to 28x28 grayed output image. sigmoid activation function is used to compare encoder input and decoder output.
Binary cross entropy is used as the loss function, and Adadelta is used as the optimizer to minimize the loss function.
import keras from keras.layers import Input, Dense from keras.models import Model from keras.datasets import mnist import numpy as np # input layer input_img = Input(shape=(784,)) # autoencoder encoding_dim = 32 encoded = Dense(encoding_dim, activation='relu')(input_img) encoded_input = Input(shape=(encoding_dim,)) decoded = Dense(784, activation='sigmoid')(encoded) autoencoder = Model(input_img, decoded) decoder_layer = autoencoder.layers[-1] decoder = Model(encoded_input, decoder_layer(encoded_input)) autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
MNIST data set is a famous handwritten numeral database, which is widely used in training and testing in the field of machine learning. We use it here to generate synthetic noise digitally by applying a Gaussian noise matrix between 0 and 1 and a clipped image.
import matplotlib.pyplot as plt
import random
%matplotlib inline
# get MNIST images, clean and with noise
def get_mnist(noise_factor=0.5):
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape)
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
return x_train, x_test, x_train_noisy, x_test_noisy, y_train, y_test
x_train, x_test, x_train_noisy, x_test_noisy, y_train, y_test = get_mnist()
# plot n random digits
# use labels to specify which digits to plot
def plot_mnist(x, y, n=10, randomly=False, labels=[]):
plt.figure(figsize=(20, 2))
if len(labels)>0:
x = x[np.isin(y, labels)]
for i in range(1,n,1):
ax = plt.subplot(1, n, i)
if randomly:
j = random.randint(0,x.shape[0])
else:
j = i
plt.imshow(x[j].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
plot_mnist(x_test_noisy, y_test, randomly=True)
You can still recognize numbers, but some are almost unrecognizable. Therefore, we want to use our automatic encoder to learn to restore the original number. By fitting more than 100 epoch self encoders, we use the noise number as the input and the original denoising number as the target.
Therefore, the self encoder will minimize the difference between noise and clean image. By doing so, it will learn how to remove noise from any invisible handwritten numeral, producing similar noise.
# flatten the 28x28 images into vectors of size 784.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
x_train_noisy = x_train_noisy.reshape((len(x_train_noisy), np.prod(x_train_noisy.shape[1:])))
x_test_noisy = x_test_noisy.reshape((len(x_test_noisy), np.prod(x_test_noisy.shape[1:])))
#training
history = autoencoder.fit(x_train_noisy, x_train,
epochs=100,
batch_size=128,
shuffle=True,
validation_data=(x_test_noisy, x_test))
# plot training performance
def plot_training_loss(history):
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'r', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plot_training_loss(history)
How to denoise with self encoder
Now we can use a trained automatic encoder to remove invisible noise input images and compare them with the cleared images.
# plot de-noised images
def plot_mnist_predict(x_test, x_test_noisy, autoencoder, y_test, labels=[]):
if len(labels)>0:
x_test = x_test[np.isin(y_test, labels)]
x_test_noisy = x_test_noisy[np.isin(y_test, labels)]
decoded_imgs = autoencoder.predict(x_test)
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test_noisy[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
return decoded_imgs, x_test
decoded_imgs_test, x_test_new = plot_mnist_predict(x_test, x_test_noisy, autoencoder, y_test)
In general, the noise is well eliminated. The white spots on the manually input image have disappeared from the cleaned image. These numbers can be visually recognized. For example, the noisy number '4' is not readable at all. Now we can read its clean version.
Denoising has an adverse impact on information quality. The reconstructed number is a little fuzzy. The decoder adds some features that are not in the original image, such as the following 8th and 9th digits, which are almost unrecognizable.

In this article, I describe an image denoising technique and provide a practical guide on how to build an automatic encoder using Python. Radiologists usually use automatic encoders to denoise MRI, US, x-ray or skin lesion images. These automatic encoders are trained on large data sets, such as the chest x-ray database of Indiana University, which contains 7470 chest x-ray images. The denoising automatic encoder can be enhanced by convolution layer to produce more effective results.