1. Definition of heap
A heap is a special kind of complete binary tree in which the father node must be greater than or equal to its child node (this is called a heap) or the father node must be less than or equal to its child node (this is called a heap).
_The so-called complete binary tree is a kind of binary tree whose nodes are arranged as full binary tree but the number of nodes is not always the same. Except for the last layer, the number of other layers is the same as full binary tree, and the last layer of nodes is arranged from left to right.
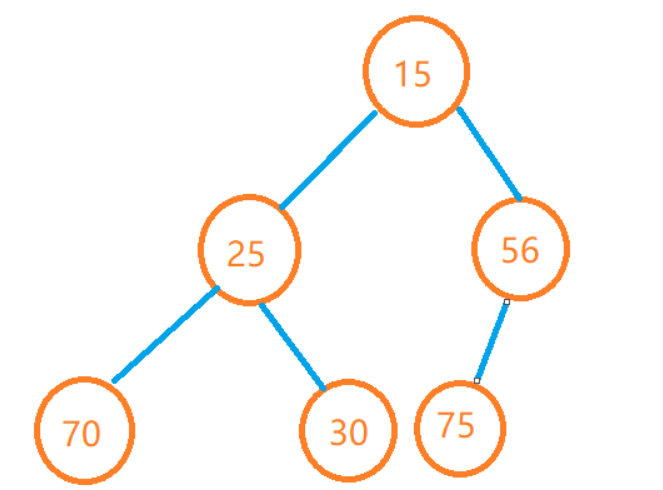
From the structure of the heap, you can see that the elements on the top of the heap must be the largest (large heap) or smallest (small heap) elements in the heap.
2. Realization of heap
1. Storage structure of the heap
_The special structure of a complete binary tree allows us to store it i n a dynamic sequence table, and we observed that an array and a complete binary tree can create a one-to-one mapping i n this way. For a node whose array size is n and whose subscript of parent node and child node can be represented as follows:
p
a
r
e
n
t
=
i
−
1
2
,
i
f
(
0
≤
p
a
r
e
n
t
)
l
e
f
t
c
h
i
l
d
=
2
∗
i
+
1
,
i
f
(
l
e
f
t
c
h
i
l
d
≤
n
−
1
)
r
i
g
h
t
c
h
i
l
d
=
2
∗
i
+
2
,
i
f
(
r
i
g
h
t
c
h
i
l
d
≤
n
−
1
)
parent = \frac{i-1}{2},if(0\leq parent)\\ leftchild = 2*i+1,if(leftchild\leq n-1)\\ rightchild = 2*i+2,if(rightchild\leq n-1)
parent=2i−1,if(0≤parent)leftchild=2∗i+1,if(leftchild≤n−1)rightchild=2∗i+2,if(rightchild≤n−1)
typedef struct Heap {
int* a;
int size;
int capacity;
}Heap;
2. Initialization, Destroy, Print, Empty, Return to Top Element of Heap
_These are things that have been talked about many times in the sequence table, so let's not repeat them.
void HeapInit(Heap* hp)
{
assert(hp);
hp->a = NULL;
hp->size = hp->capacity = 0;
}
void Heapdestroy(Heap* hp)
{
assert(hp);
free(hp->a);
hp->capacity = hp->size = 0;
hp->a = NULL;
}
void HeapPrint(Heap* hp)
{
assert(hp);
for (int i = 0; i < hp->size; i++)
{
printf("%d ", hp->a[i]);
}
printf("\n");
}
bool HeapEmpty(Heap* hp)
{
return hp->size == 0;
}
int HeapSize(Heap* hp)
{
return hp->size;
}
int HeapTop(Heap* hp)
{
assert(hp);
assert(!HeapEmpty(hp));
return hp->a[0];
}
_To introduce two core algorithms for heap creation: the up-adjustment algorithm and the down-adjustment algorithm, we first introduce the insertion and deletion of heaps.
3. Insertion of heap
_Assuming that we already have a heap, if we want to insert elements in the heap, the first position must be at the end of the array, but insertion does not necessarily satisfy the heap structure anymore. In this case, we need to analyze it carefully.

_Found that each insertion will only affect the node on the path from the current node to the root node, and will not affect other nodes. Take the heap as an example, the value of other nodes satisfies the nature of the heap. The parent node must be larger than the child node, then you adjust the root node, the root node will only be larger, and the heap relationship of other nodes will not change.
_Depending on this nature, we can design an up-scaling algorithm that compares the current node with its parent node (if it exists). For example, in a small heap, if the current node is smaller than the parent node, we exchange the values of the current node and the parent node, and then look at the new current node and the parent node. Exit until the current node is larger than the parent node or the current node is already the root node.
void swap(HPDataType* x, HPDataType* y)
{
assert(x && y);
HPDataType tmp = *x;
*x = *y;
*y = tmp;
}
//Adjust up from child
//Worst case adjustment layer several times, O(logn)
void AdjustUp(HPDataType* a, int n, int child)
{
assert(a);
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 4 : 2 * hp->capacity;
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
printf("ralloc fail\n");
exit(-1);
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size] = x;
hp->size++;
AdjustUp(hp->a, hp->size, hp->size - 1);
}
_There's something interesting about adjusting the algorithm up here if we change the while loop condition to:
while (parent >= 0)//Obviously, this is designed to jump out of parent = (0-1)/2<0 when child=0
_This is wrong, but not entirely wrong, because after the last child=0, parent=(0-1)/2=0, or 0, is not less than 0 as expected because of the rounding mechanism.
_So how do you get out in this way? Because parent == child ==0, a[parent] == a[child], will go out of else.
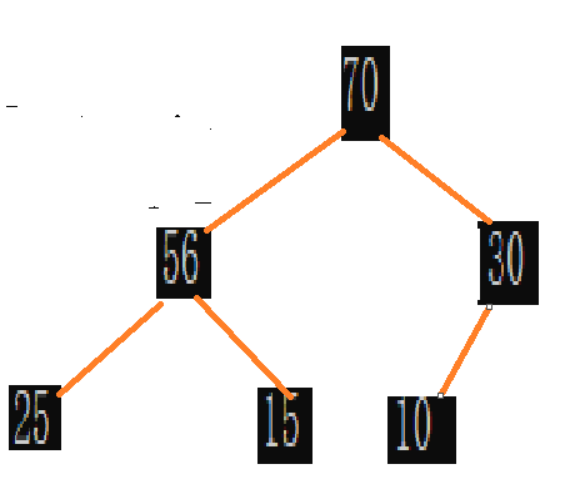
_This is like the following picture. You said it was clever, it doesn't seem to be, but you said it was wrong, but people have the same effect as the correct code.

_heap insertions are adjusted at most a few times, so the time complexity is O(logn)
4. Remove heap top elements
_Removing the top element is a clever method. First we exchange the top element with the last element in the current heap, then the heap size-1 to remove the last element. Then the characteristics of the heap are destroyed and need to be adjusted.
_A downward adjustment algorithm is needed here. Take the heap for example, swap the top element with its smaller child, and then move down until there is no child or he is older than the younger of his children and jumps out of the loop.
//Worst case O(logn) to adjust layer number of times
void AdjustDown(int* a, int n, int parent)
{
assert(a);
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child+1] > a[child])
{
child++;
}
if (a[child] > a[parent])
{
swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapPop(Heap* hp)
{
assert(hp);
assert(!HeapEmpty(hp));
swap(&hp->a[0], &hp->a[hp->size - 1]);
hp->size--;
AdjustDown(hp->a, hp->size, 0);
}
The same is true for removing top heap elements, adjusting down at most, cycling layers several times, and time complexity being O(logn).
5. Two algorithms for creating heaps
_We already have an up-scaling algorithm and a down-scaling algorithm:
void AdjustUp(HPDataType* a, int n, int child); //Adjust up the array a of the storage heap that needs to be adjusted, the size n of the array, and the subscript child at the beginning void AdjustDown(int* a, int n, int parent);//n is the array size //Adjust down where adjustment begins parent
_If you really want to create a heap, the easiest way is to insert array elements constantly into the heap, but this idea has O(N) spatial complexity. We want to control an array without creating additional arrays, that is, to control the structure of the array into a heap with O(1) spatial complexity.
Idea 1: Using the up-scaling algorithm
_The general idea is to always control the nature of the heap that elements in the current array satisfy, that is, to continuously adjust the algorithm upwards from the second element to the first element, which uses the idea of false insertion. The algorithm upwards from the second element is actually to insert the second element, the third element... the nth element into the heap. But they're already in the array.
//Build a into a heap array A whose size is n
//Method 1
//Using the idea of insertion is equivalent to inserting one at a time at the leaf node and then adjusting it up
for (int i = 1; i < n; i++)
{
AdjustUp(a, n, i);
}
void createHeap(Heap* hp, int* a, int n)
{
assert(hp);
assert(a);
for (hp->size = 0; hp->size < n; hp->size++)
{
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 4 : 2 * hp->capacity;
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
printf("ralloc fail\n");
exit(-1);
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size] = a[hp->size];
}
for (int i = 1; i < n; i++)
{
AdjustUp(hp->a, n, i);
}
}
Idea 2: Using the down-scaling algorithm
_Note that if we adjust the algorithm downward for the first non-leaf node so that a complete binary tree with this non-leaf node as the root node satisfies the nature of the heap, then we can adjust the algorithm downward from the first non-leaf node to the root node, which is equivalent to continuously increasing the top elements of the heap. It then adjusts down so that the subheap satisfies the nature of the heap.
Notice that the first non-leaf node is the parent of the last element of the array, that is:
n
−
1
−
1
2
\frac{n-1-1}{2}
2n−1−1
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
void createHeap(Heap* hp, int* a, int n)
{
assert(hp);
assert(a);
for (hp->size = 0; hp->size < n; hp->size++)
{
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 4 : 2 * hp->capacity;
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
printf("ralloc fail\n");
exit(-1);
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size] = a[hp->size];
}
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(hp->a, n, i);
}
}
6. Time complexity analysis of heap creation
_Adjust up to create a heap
for (int i = 1; i < n; i++)
{
AdjustUp(a, n, i);
}
_You might think that this is not an outer loop n times, and the time complexity of adjusting the time up inside the loop is O(logn), so is the time complexity O (n logn). In this case, you ignore the fact that not every element is adjusted up from the bottom of the heap.
_For example, we have made a false insert, the second element is in the second layer of the heap, it only needs to be adjusted once at most, the third element is still in the second layer, it only needs to be adjusted once at most, the fourth element is in the third layer, it needs to be adjusted twice at most, the fifth element is in the third layer, it needs to be adjusted twice at most, and the sixth element is also in the third layer. You need to adjust it at most two times, the seventh element at the sixth level and at most two times, the eighth element at the fourth level and at most three times.
_For easy estimation, we consider that the heap is a complete binary tree with n nodes and h-layers.

- Layer 2 ^1 elements move up 1 layer
- Layer 3 2^2 elements move up 2 layers
- Layer 4 2^3 elements move up 3 layers
...
- Layer h 2^(h-1) elements move up layer H-1
T ( n ) = 1 ∗ 2 1 + 2 ∗ 2 2 + 3 ∗ 2 3 + . . . + ( h − 1 ) ∗ 2 h − 1 T(n)=1*2^{1}+2*2^{2}+3*2^{3}+...+(h-1)*2^{h-1}\\ T(n)=1∗21+2∗22+3∗23+...+(h−1)∗2h−1
Perform a dislocation subtraction with:
2
T
(
n
)
=
1
∗
2
2
+
2
∗
2
3
+
.
.
.
+
(
h
−
2
)
∗
2
h
−
1
+
(
h
−
1
)
∗
2
h
−
T
(
n
)
=
2
1
+
2
2
+
.
.
.
+
2
h
−
1
−
(
h
−
1
)
∗
2
h
=
2
h
−
2
−
(
h
−
1
)
2
h
T
(
n
)
=
(
h
−
2
)
2
h
−
2
=
(
l
o
g
2
(
n
+
1
)
−
2
)
(
n
+
1
)
−
2
T
(
n
)
−
>
O
(
n
l
o
g
n
)
2T(n)=1*2^2+2*2^3+...+(h-2)*2^{h-1}+(h-1)*2^{h}\\ -T(n)=2^1+2^2+...+2^{h-1}-(h-1)*2^{h}\\=2^h-2-(h-1)2^h\\ T(n)=(h-2)2^h-2=(log_{2}(n+1)-2)(n+1)-2\\ T(n)->O(nlogn)
2T(n)=1∗22+2∗23+...+(h−2)∗2h−1+(h−1)∗2h−T(n)=21+22+...+2h−1−(h−1)∗2h=2h−2−(h−1)2hT(n)=(h−2)2h−2=(log2(n+1)−2)(n+1)−2T(n)−>O(nlogn)
_Does it feel like I've been tossing around half a day of complexity here? That's O(nlogn). Don't worry, the game is just beginning.
_For downward adjustment,
- Layer 1, 2^0 elements, move down layer h-1
- Layer 2, 2^1 elements, move down layer h-2
- ...
- Layer h-1, 2^(h-2) elements, move down layer 1
T ( n ) = ( h − 1 ) ∗ 2 0 + ( h − 2 ) ∗ 2 1 + ( h − 3 ) ∗ 2 2 + . . . + 1 ∗ 2 h − 2 T(n)=(h-1)*2^{0}+(h-2)*2^{1}+(h-3)*2^{2}+...+1*2^{h-2} T(n)=(h−1)∗20+(h−2)∗21+(h−3)∗22+...+1∗2h−2
Perform a dislocation subtraction:
2
T
(
n
)
=
(
h
−
1
)
2
1
+
(
h
−
2
)
2
2
+
.
.
.
+
2
∗
2
h
−
2
+
1
∗
2
h
−
1
T
(
n
)
=
2
1
+
2
2
+
.
.
.
+
2
h
−
2
+
2
h
−
1
−
h
+
2
0
T
(
n
)
=
2
h
−
1
−
h
from
n
=
2
h
−
1
Yes
T
(
n
)
=
n
−
l
o
g
2
(
n
+
1
)
T
(
n
)
−
>
O
(
n
)
2T (n) = (h-1) = (h-1) 2^1+ (h-2) 2^2+...+2*2^{h-2}+h-2}+1*2^{{{h-1} \\\\\\T(n) =2^1+2^{{h-1} ^^{h-1}-h-1}-h+2^^^2^^2 ^^{{h-1} -h-1}-h+2^0 \\\\^2^^^(n) =n-log_ {2} (n+1)\T(n)->O(n)
2T(n)=(h_1)21+(h_2)22+...+2_2h_2+1_2h_1T(n)=21+22+...+2h_2+2h_1_h+20T(n)=2h_1_h from n=2h_1 has T(n)=n_log2(n+1)T(n) O(n)
_Therefore, it is best to create a heap by adjusting it downwards with O(n) time complexity.
3. TOPK Issues
TOP-K problem: The first K largest or smallest elements in the data combination are usually large. For example: Top 10 professional, Top 500, Rich List, Top 100 active players in the game, etc.
_Abstract is to find the largest first k of N numbers.
Idea 1: Sort (O (NlogN)) and take out the first k, time complexity O (NLogN)
Idea 2: Create a heap of N elements, then pop k times, build time complexity O(N), POPk time complexity O(klogN), total time complexity O(N+klogN)
However, there is a problem. Normally, N is very large, and these numbers cannot be stored in memory. They exist in files, and sorting cannot exclude the largest first k. Because the largest first k may not be in the number that you can store in memory, Ideas 1 and 2 cannot be used, because these data cannot be read into memory completely.
Idea 3:
- Use the first k to build a small k-number heap.
- Compare the subsequent N-K data to the top of the heap element in turn. If it is larger than the top of the heap, replace the top of the heap and adjust it down.
- The number of K in the heap is the first 100 larger numbers. (The elements outside your heap must be smaller than those on the top, so the first k is chosen.)
Time complexity O(k+(N-k)logk)~O(N), and efficiency is good.
void PrintTopK(int* a, int n, int k)
{
Heap hp;
HeapInit(&hp);
createHeap(&hp, a, k);
for (int i = k; i < n; i++)
{
if (a[i] > HeapTop(&hp))
{
//Call interface only
HeapPop(&hp);
HeapPush(&hp, a[i]);
//Direct Access Structures
//hp.a[0] = a[i];
//AdjustDown(hp.a, hp.size, 0);
}
}
HeapPrint(&hp);
Heapdestroy(&hp);
}
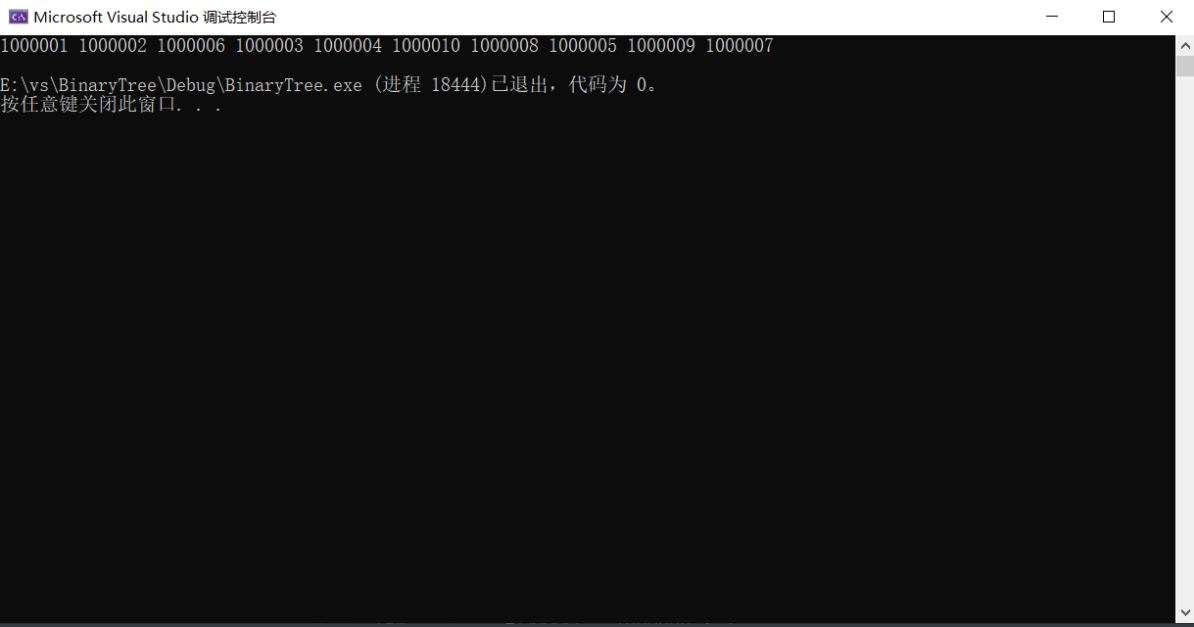
void TestTopk()
{
int n = 1000000;
int* a = (int*)malloc(sizeof(int) * n);
srand(time(0));
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
//Set 10 larger than 1000000
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2335] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 9;
a[3144] = 1000000 + 10;
PrintTopK(a, n, 10);
}
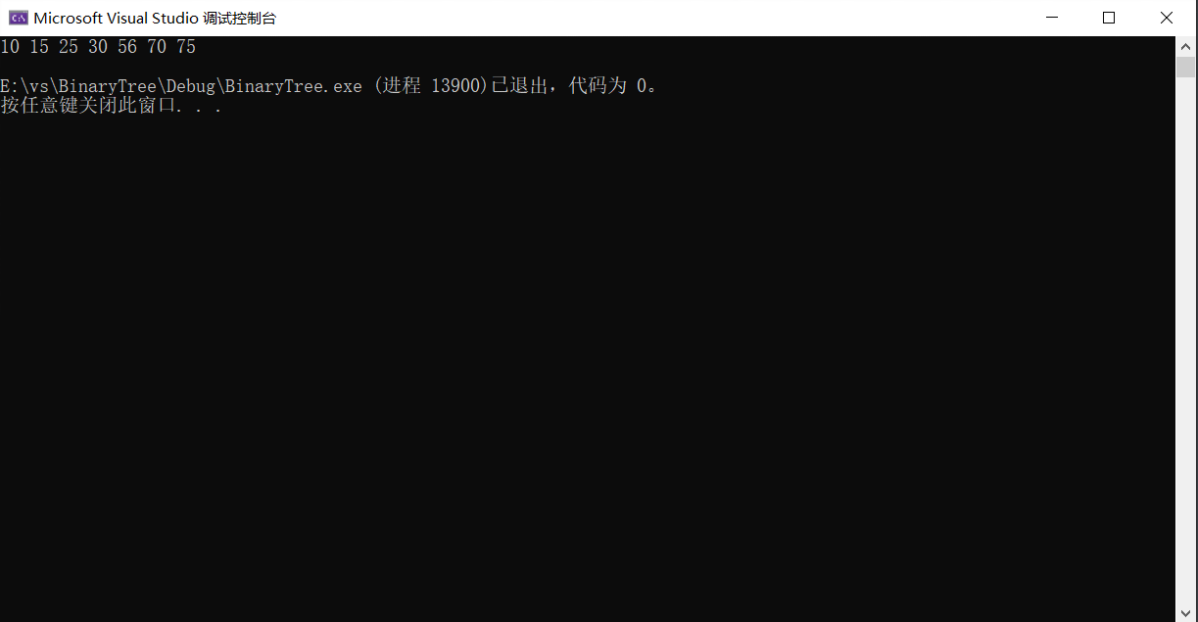
4. Heap Sorting
_If you don't have a requirement for spatial complexity, it's really easy. Build a heap, put the array in the heap, and popn times, but the spatial complexity is O(N).
_But if I limit the space complexity to O(1), then we'll have to manipulate the array ourselves, use the algorithm we mentioned in Creating Heaps, and adjust the algorithm down because it's less time complex.
_Take ascending order for example, if we want to create a heap or a heap, we can't build a heap here, because the first element is really the smallest, but then other elements need to rebuild the heap, otherwise the parent-child relationship between heaps has been destroyed (think subscript), the time complexity of rebuilding a heap under is:
O
(
n
)
+
O
(
n
−
1
)
+
.
.
.
O
(
1
)
=
O
(
n
2
)
O(n)+O(n-1)+...O(1) = O(n^{2})
O(n)+O(n−1)+...O(1)=O(n2)
_Then why don't I find the smallest one time in a loop, so using heaps doesn't really reflect the advantage of using heaps.
_So ** Heap sorting establishes a large heap in ascending order and a small heap in descending order. ** The ideas are as follows:
- Build a heap, where the first element is the largest, swapping the last element with the first.
- The last element is already the largest element, which does not need to be arranged anymore, just as long as it is not treated as an element in the heap (that is, the number of elements in the heap is treated as n-1), then the top of the heap is adjusted down, a large heap is built again, and then replaced.
void HeapSort(int* a, int n)
{
assert(a);
if (n == 1)
return;
//Build reactor O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//O(NlogN)
for (int i = n - 1; i > 0; i--)
{
swap(&a[0], &a[i]);
AdjustDown(a, i, 0);
}
}
void test3()
{
int a[] = { 70, 56, 30, 25, 15, 10, 75 };
HeapSort(a, sizeof(a) / sizeof(a[0]));
for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
test3();
return 0;
}