Let's take a look at the definition given by Du Niang:
And look up the set. In some set application problems with N elements, we usually make each element form a single element set at the beginning, and then merge the sets of elements belonging to the same group in a certain order. In the meantime, we should repeatedly find out which set an element is in. In recent years, such problems have repeatedly appeared in the international and domestic competitions of informatics. Its characteristic is that it does not seem complex, but the amount of data is huge. If it is described with normal data structure, it is often too large in space for the computer to bear; Even if we barely pass in space, the running time complexity is also very high. It is impossible to calculate the results required by the test questions within the running time specified in the competition (1 ~ 3 seconds), which can only be described by parallel search.
To sum up:
If we have a large set of elements, we need to call the following two operations frequently:
- Merge two element intervals
- Determine whether two elements are in a set
If we don't have a search set, the time complexity of performing these two operations will be very high in the face of a large amount of data
If we use the structure of parallel query set, although the time complexity of a single operation may be O(n), if we call these two functions frequently, the average time complexity can reach O(1)
We don't prove this conclusion. (after all, the big guys have proved it for more than 20 years. How can I prove it in such a short time (whisper))
Cough, in a word, just remember the above conclusion
This structure can solve some problems that need to count the number of sets
Implementation of parallel search set
Give a definition first:
The pointer points to its own node. We call it the representative node of the set. It exists as the most vertex (parent node) identifying the set
If we have an integer array, we need to implement it into a union search set
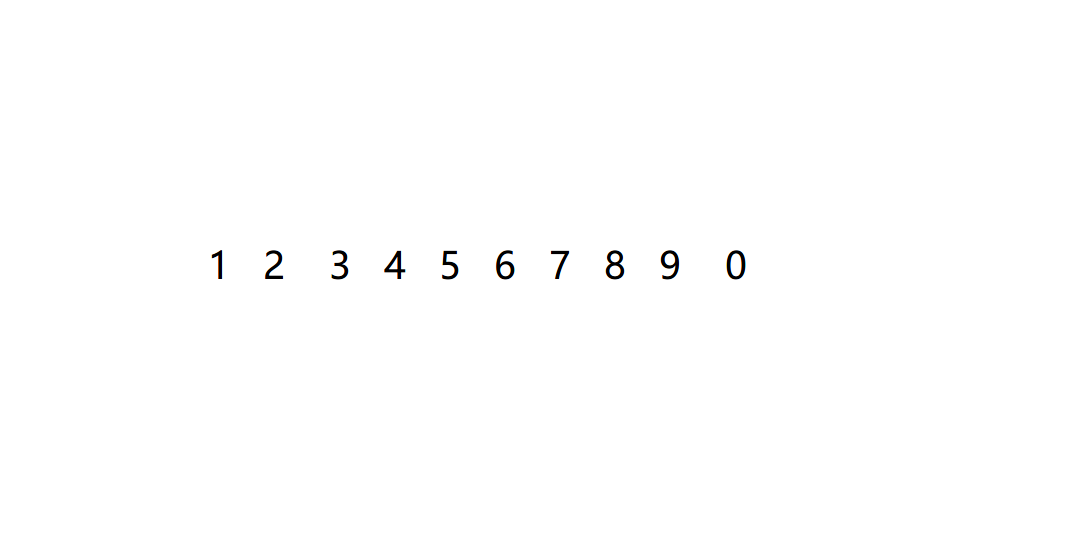
When we initialize, we first treat each element as a separate set
That is to point out a pointer to yourself
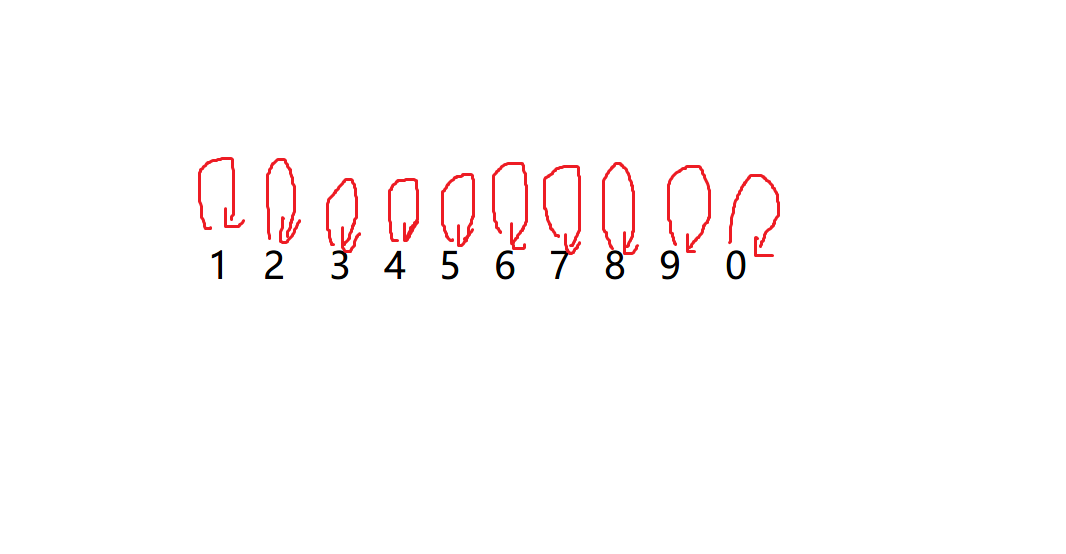
This completes our initialization, that is, the representative node of each element is itself
Therefore, it is very simple for us to judge whether the elements come from the same set. We can directly judge whether their representative nodes are the same
The operations of merging are as follows:
In this case, if we want to merge the set of 1 and 2 elements, we can hang the parent node of one element set on another parent node
We might as well hang 2 on 1
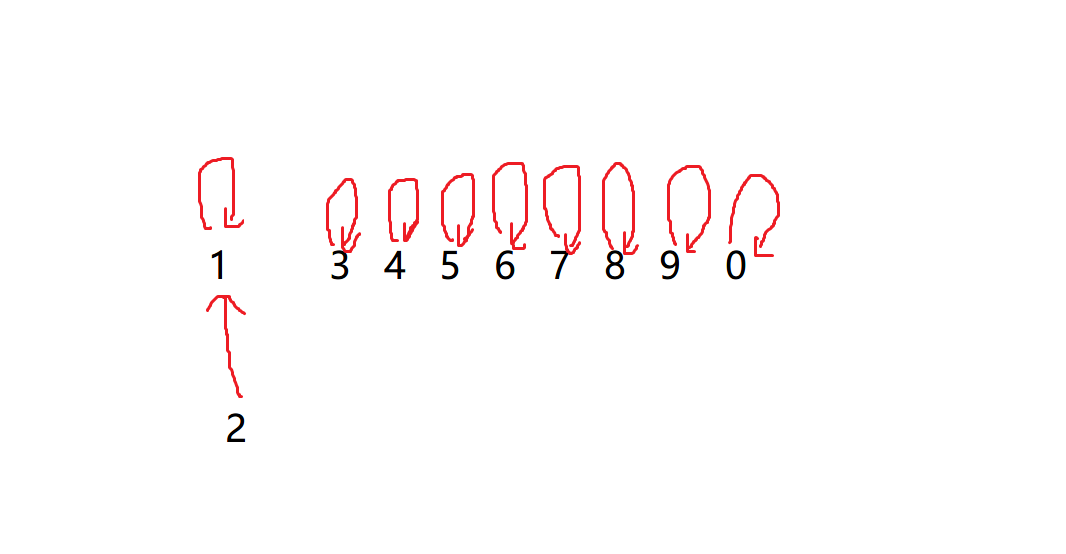
In this way, we have completed an element merging
If we want to merge 2 and 3 this time, what should we do?
Similarly, just hang the parent node of one set to the parent node of another element
However, in this case, it should be noted that in order to speed up efficiency, we usually hang the parent node of a small set on the parent node of a large set
Like this
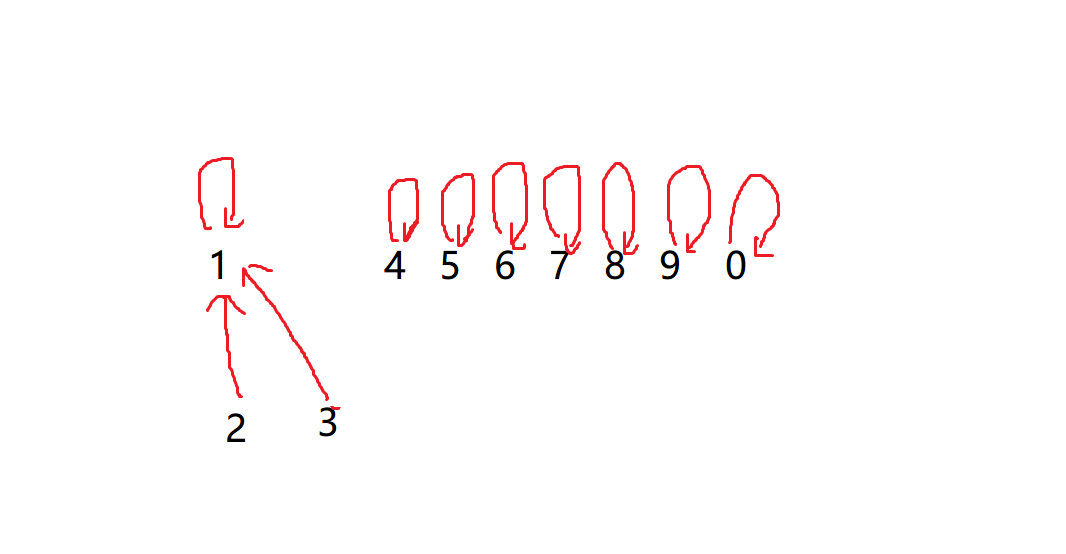
But in this process, we still need some operations
For example, how to find the representative node of the set where an element is located? How to quickly find representative nodes? It is described in detail in the following code implementation
We need the following structure to implement:
An array that records the subscript position of the key node of an element, the size of the set where the current element is located, and the number of the current set
vector<int>parent;//Record the key node at this position, such as parent[i]=a, and the element representing the I subscript is at a vector<int>size;//Record the size of the set of key nodes. It is only valid for key nodes, and set non key nodes to 0 vector<int>help;//Auxiliary array, which will be introduced later int sets;//Record the number of current query sets
During initialization, we need to know and check the number of elements in the initial set. According to the setting that each element has a set in the initial set, we can quickly write the following initialization code:
int n = nums.size();//How many elements are there in our array, and how many sets are opened initially
parent.resize(n);
size.resize(n);
help.resize(n);
sets = n;
for (int i = 0; i < n; i++)
{
parent[i] = i;//Key nodes for themselves
size[i] = 1;//The collection size is 1
}
Because in the above operation, you need to frequently find the location of key nodes, so you also need to implement a function to find the location of key nodes
The principle is simple:
If the subscript of the parent[i] record of an element is not the subscript of the element itself, it means that the node is not the representative node. We find the subscript through the position of the parent array record and iterate until the key node is found
//This function finally returns the representative node subscript of the element in the current subscript
int findfather(int i)
{
while (i != parent[i])
{
i = parent[i];
}
return i;
}
But in some extreme cases, if such frequent calls occur, the time complexity of each call is O(n)
For example, the elements are all on a chain, forming a structure similar to a linked list. We can find it from the lowest element
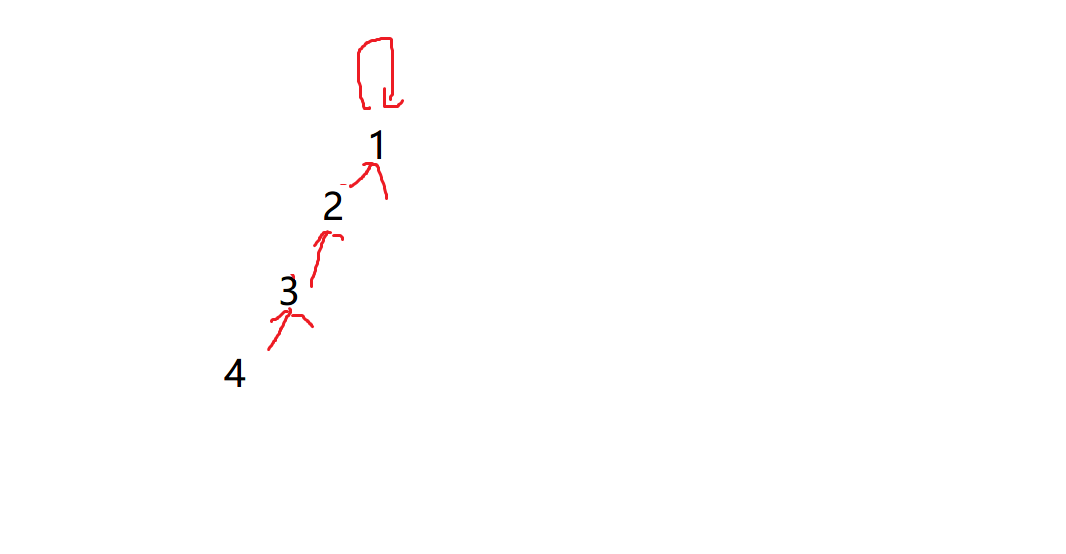
If we don't do any optimization, the average time complexity is O(n)
We can optimize the compression path:
The specific implementation is as follows:
Every time we traverse the array, we put the following elements in the help

Then compress the path. We pop up each element in help in turn, and then set the representative node of each element as the current return value
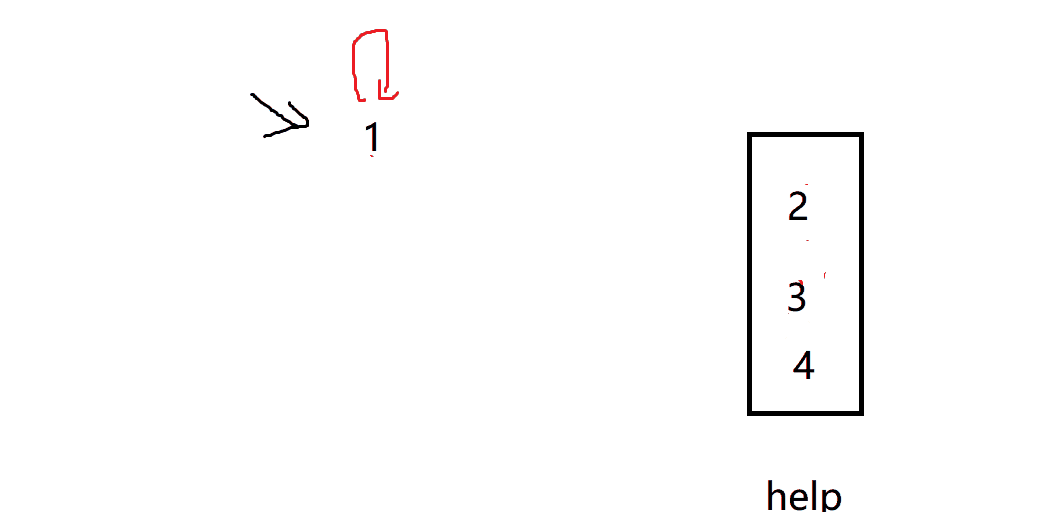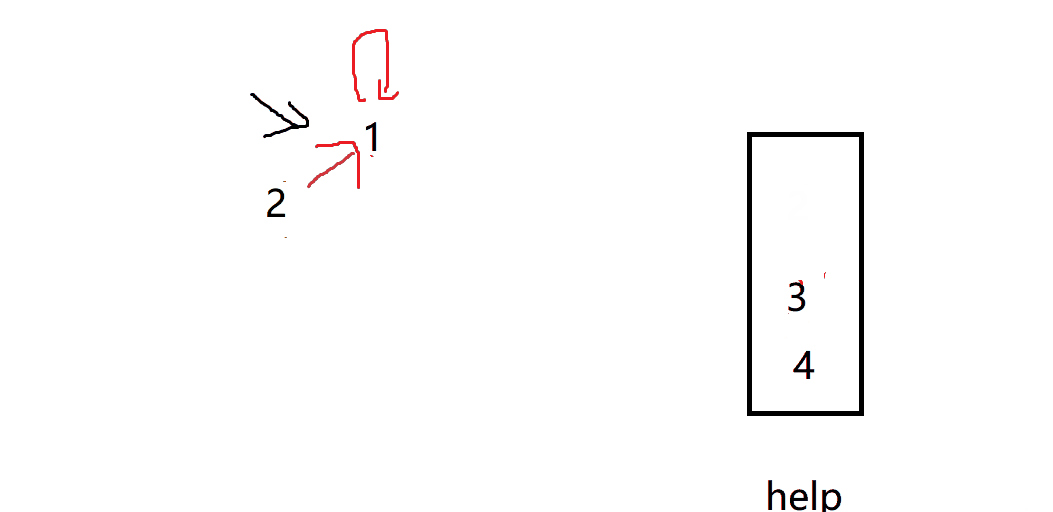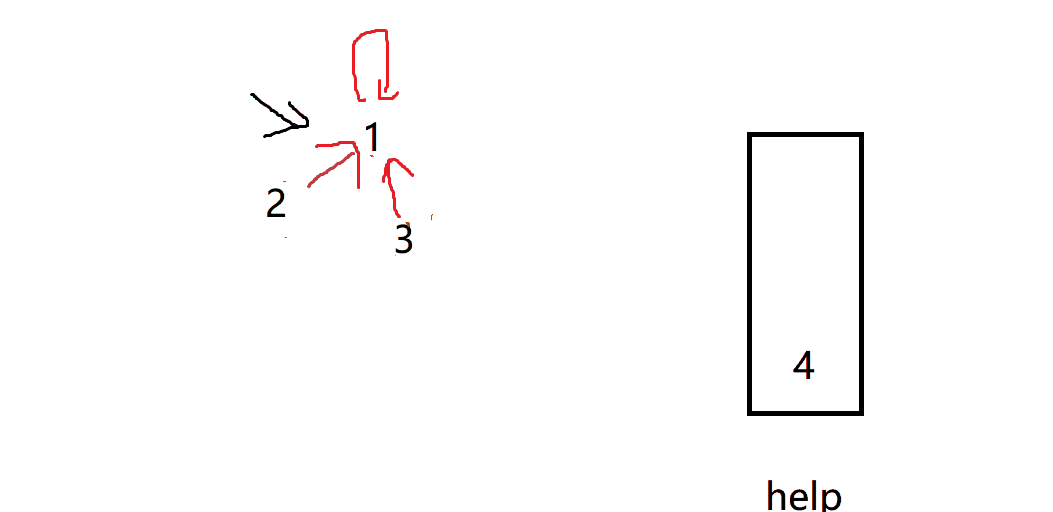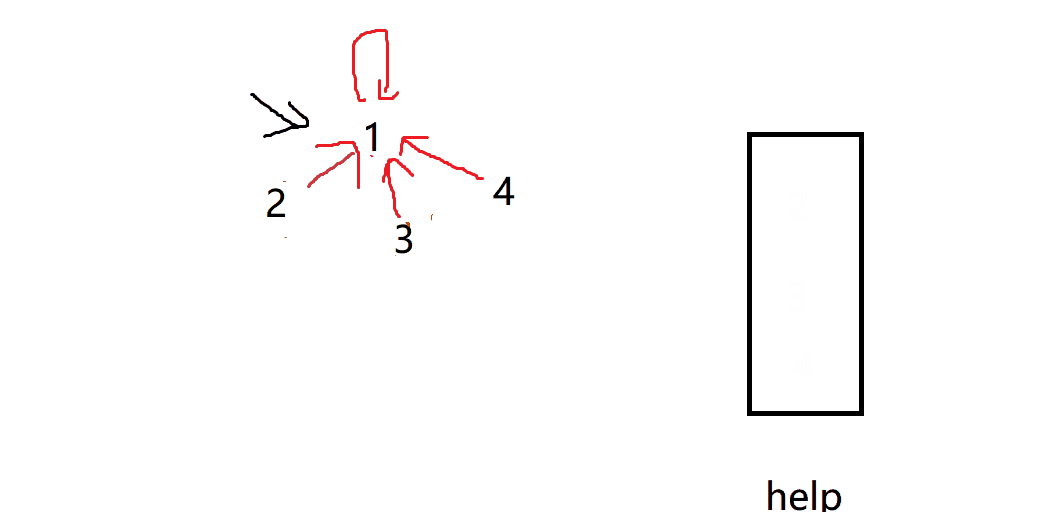
In this way, each element points to a unique representative node
Summary:
The help array mentioned earlier is used here as a stack
Although the time complexity of a single search may be O(n), after our path compression, if we repeatedly search the elements in this set in the future, the time complexity will be O(1)
Because our premise is a large number of repeated operations, the average time complexity is O(1)
Complete search representative node code:
int findfather(int i)
{
int hi = 0;
while (i != parent[i])
{
help[hi++] = i;
i = parent[i];
}
for (hi--; hi >= 0; hi--)//Remember first--
{
parent[help[hi]] = i;//Path compression operation
help[hi] = 0;
}
return i;
}
Next, let's implement the two methods mentioned at the beginning of the article
Note: when we use these two methods, the parameters are passed to the subscript in the original array
It's easy to find out whether they are the same elements. You can directly judge whether they are equal
bool isSameFather(int i, int j)
{
return findfather(i) == findfather(j);
}
The operations during merging are as follows:
First, find out the representative nodes of the set where the elements are located
int A = findfather(i); int B = findfather(j);
At this time, judge that if A=B, it means that the two elements come from the same set, there is no need to merge. Just exit the function directly
Because we hang a small set on a large set, we need to judge which of a and B is a large set
int big = size[A] >= size[B] ? A : B; int small = big == A ? B : A;
Then perform the merge operation: change the position of the representative node, change the size value, change the number of sets, etc
parent[small] = big; size[big] += size[small]; size[small] = 0; sets--;//Merging one represents that there is one less set in the query set
In most cases, we may also need to return and check the number of elements in the set
int getSets()
{
return sets;
}
The complete code is as follows
class Union2
{
public:
Union2(vector<int>& nums)
{
int n = nums.size();
parent.resize(n);
size.resize(n);
help.resize(n);
sets = n;
for (int i = 0; i < n; i++)
{
parent[i] = i;
size[i] = 1;
}
}
bool isSameFather(int i, int j)
{
return findfather(i) == findfather(j);
}
int getSets()
{
return sets;
}
void together(int i, int j)//It's a subscript
{
int A = findfather(i);
int B = findfather(j);
if (A != B)
{
int big = size[A] >= size[B] ? A : B;
int small = big == A ? B : A;
parent[small] = big;
size[big] += size[small];
size[small] = 0;
sets--;
}
}
private:
vector<int>parent;//Record the key nodes at this location
vector<int>size;//Record the location of key nodes
vector<int>help;//Make stack
int sets;//Number of record sets
int findfather(int i)
{
int hi = 0;
while (i != parent[i])
{
help[hi++] = i;
i = parent[i];
}
for (hi--; hi >= 0; hi--)//Remember first--
{
parent[help[hi]] = i;
help[hi] = 0;
}
return i;
}
};
In addition, add the implementation of hash table, and save the hash as a pointer node. Everything else is the same
class Node
{
public:
Node(int x)
:val(x)
{}
private:
int val;
};
class Union
{
private:
unordered_map<int, Node*>node;//Value and node corresponding to value
unordered_map<Node*, Node*>parent;//Node and its representative node
unordered_map<Node*, int>size;//Represents a node and its corresponding set size
Node* findfather(Node* n)
{
stack<Node*>path;
Node* cur = n;
while (parent[cur] != cur)
{
cur = parent[cur];
path.push(cur);
}
if (!path.empty())
{
Node* now = path.top();
parent[now] = cur;
path.pop();
}
return cur;
}
public:
Union(vector<int>& nums)
{
for (auto i:nums)
{
Node* n = new Node(i);
node[i] = n;
parent[n] = n;
size[n] = 1;
}
}
bool isSameUnion(int a, int b)
{
return findfather(node[a]) == findfather(node[b]);
}
int setsize()
{
return size.size();
}
void together(int a, int b)
{
Node* A = findfather(node[a]);
Node* B = findfather(node[b]);
if (A != B)
{
Node* big = size[A] >= size[B] ? A : B;
Node* small = A == big ? B : A;
parent[small] = big;
size[big] += size[small];
size.erase(small);
}
}
};
Parallel search set application
Force deduction 547, number of provinces
Title Description:
There are n cities, some of which are connected to each other, others are not connected. If city a is directly connected to city b and city b is directly connected to City c, city a is indirectly connected to city c.
A province is a group of directly or indirectly connected cities, excluding other cities that are not connected.
Give you an n x n matrix isConnected, where isConnected[i][j] = 1 indicates that the ith city and the jth city are directly connected, and isConnected[i][j] = 0 indicates that they are not directly connected.
Returns the number of provinces in the matrix.
For example: Enter: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2 (because 1 and 2 cities are connected, one of 1 and 2 is not the capital)
Solution ideas:
This problem is a typical problem of the number of sets returned by merging and searching sets
If there are three cities of 0, 1 and 2, let 0, 1 and 2 respectively represent the horizontal and vertical coordinates in the array. If there are roads between them, set their intersection in the array as 1, and vice versa as 0
We can get the following properties of the array: the elements on the diagonal are always 1, because they must be related to themselves
This array must be a symmetric matrix. If there is a connection between (1,2), then there must be a connection between (2,1)
Therefore, when traversing, we only need to traverse the elements above the diagonal of the array
Because there are several cities in the initial row, when we initialize and query the set, we only need to transfer the size. Initially, each city is the capital, that is, each node is a representative node
If there is a connection, merge the two cities
The code is as follows:
class Union//Union search set
{
public:
Union(int n)//As many cities as there are, it is initially assumed that each city is the capital
{
parent.resize(n);
size.resize(n);
help.resize(n);
set=n;
for(int i=0;i<n;i++)
{
parent[i]=i;//The initial parent node points to itself
size[i]=1;//Each collection has only one element
}
}
bool isSameFather(int i,int j)//Observe whether it belongs to the same element
{
return findFather(i)==findFather(j);
}
void together(int i,int j)//Merge a collection of two elements
{
int A=findFather(i);
int B=findFather(j);//Find their representative nodes first
if(A!=B)//Unequal operation
{
//In order to improve efficiency, hang the small collection under the large collection
int big=A>=B?A:B;
int small=big==A?B:A;
parent[small]=big;//Change the representative node
size[big]+=size[small];
size[small]=0;
set--;
}
}
int getSet()
{
return set;
}
private:
vector<int>parent;//Where is the father of a subscript position
vector<int>size;//Represents the number of sets representing nodes
vector<int>help;//Used as a stack when compressing paths
int set;//Number of record sets
int findFather(int i)//Pass in the subscript and return the subscript representing the node
{
int hi=0;
while(parent[i]!=i)//Judge whether the father of the element is himself, stop or iterate
{
help[hi++]=i;
i=parent[i];
}
//Path compression
for(hi--;hi>=0;hi--)
{
parent[help[hi]]=i;
help[hi]=0;
}
return i;
}
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int n=isConnected.size();
Union u(n);
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)//You only need to traverse the elements in the upper right corner
{
if(isConnected[i][j]==1)
{
u.together(i,j);
}
}
}
return u.getSet();
}
};
Force deduction 200, number of islands
Give you a two-dimensional grid composed of '1' (land) and '0' (water). Please calculate the number of islands in the grid.
Islands are always surrounded by water, and each island can only be formed by adjacent land connections in the horizontal and / or vertical direction.
In addition, you can assume that all four sides of the mesh are surrounded by water.
For example:
Input: grid =[
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
Output: 3
Thinking solution
This problem actually has a recursive infection method, but it is not the focus of this chapter, so I only post the code and don't explain it in detail
class Solution {
public:
void infect(vector<vector<char>>& grid,int r,int c)
{
//In order to prevent dead recursion during infection, the numbers are changed to 2
if(r<0||c<0||r>=grid.size()||c>=grid[0].size()||grid[r][c]!='1')
{
return;
}
grid[r][c]='2';
infect(grid,r-1,c);
infect(grid,r+1,c);
infect(grid,r,c-1);
infect(grid,r,c+1);
}
int numIslands(vector<vector<char>>& grid) {
//Recursive infection method
int ans=0;
int r=grid.size();
int c=grid[0].size();
for(int i=0;i<r;i++)
{
for(int j=0;j<c;j++)
{
if(grid[i][j]=='1')
{
ans++;
infect(grid,i,j);
}
}
}
return ans;
}
};
Let's focus on the implementation method of this problem
First of all, let's have an array of row s and columns when we initialize the colrow
We can convert two-dimensional coordinates into one-dimensional array. The conversion formula is as follows:
int index(int i,int j)
{
return i*col+j;
}
At the beginning, we first traverse the whole map. As long as there is an island, we initialize its corresponding coordinates. At the beginning, each 1 is regarded as an independent island
In order to prevent missing numbers, when we traverse, observe whether there are islands in the upper left position of the course position, and merge if there are
int index(vector<vector<char>>& grid,int i,int j)
{
return i*grid[0].size()+j;
}
class Union2
{
public:
Union2(vector<vector<char>>& grid)
{
//Pay special attention to this problem and look up the structure of the set
//Convert the parallel search set into a one-dimensional array, store elements in the corresponding position of the subscript of the two-dimensional array, and do not process others. Only when traversing each 1 can the corresponding position of the parallel search set be processed
int n=grid.size()*grid[0].size();
parent.resize(n);
size.resize(n);
help.resize(n);
sets=0;
for(int i=0;i<grid.size();i++)
{
for(int j=0;j<grid[0].size();j++)
{
if(grid[i][j]=='1')
{
int k=index(grid,i,j);
parent[k]=k;
size[k]++;
sets++;//The number of sets increases dynamically
}
}
}
}
bool isSameFather(int i, int j)
{
return findfather(i) == findfather(j);
}
int getSets()
{
return sets;
}
void together(int i, int j)//It's a subscript
{
int A = findfather(i);
int B = findfather(j);
if (A != B)
{
int big = size[A] >= size[B] ? A : B;
int small = big == A ? B : A;
parent[small] = big;
size[big] += size[small];
size[small] = 0;
sets--;
}
}
private:
vector<int>parent;//Record the key nodes at this location
vector<int>size;//Record the location of key nodes
vector<int>help;//Make stack
int sets;//Number of record sets
int findfather(int i)
{
int hi = 0;
while (i != parent[i])
{
help[hi++] = i;
i = parent[i];
}
for (hi--; hi >= 0; hi--)//Remember first--
{
parent[help[hi]] = i;
help[hi] = 0;
}
return i;
}
};
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
Union2 u(grid);
for(int j=1;j<grid[0].size();j++)
{
if(grid[0][j-1]=='1'&&grid[0][j]=='1')
{
u.together(index(grid,0,j-1),index(grid,0,j));
}
}
for(int i=1;i<grid.size();i++)
{
if(grid[i-1][0]=='1'&&grid[i][0]=='1')
{
u.together(index(grid,i-1,0),index(grid,i,0));
}
}
//The first two for loops deal with boundaries
for(int i=1;i<grid.size();i++)
{
for(int j=1;j<grid[0].size();j++)
{
if(grid[i][j]=='1')
{
if(grid[i-1][j]=='1')
{
u.together(index(grid,i-1,j),index(grid,i,j));
}
if(grid[i][j-1]=='1')
{
u.together(index(grid,i,j),index(grid,i,j-1));
}
}
}
}
return u.getSets();
}
};