Implementation and application of treap

Implementation and application of tread

concept

Tree is a combination of tree+heap. As its name suggests, it has the properties of both heap and binary search tree

Each node in the tree has two attributes A A A and B B B. Among them A A The A attribute conforms to the nature of the heap: the of any node A A A is less than (or greater than) his son's A A A；

And properties B B B conforms to the nature of binary search tree: the of any node B B B is greater than that of all nodes in its left subtree B B B value, which is less than that of all nodes in its right subtree B B B value.

As shown in the following figure: letters represent A attribute and numbers represent B attribute.

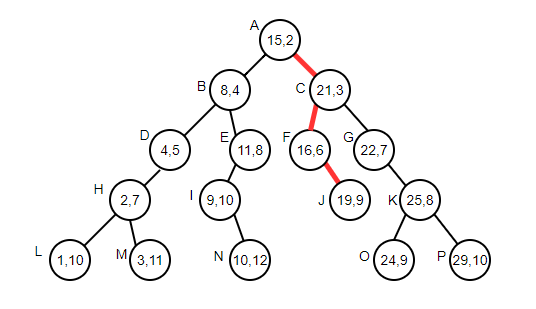
Let's review the construction process of binary search tree. If the input data gives the value of each node in turn, and the value of the node happens to be strictly increasing or decreasing, we will get a chain. If we randomly disrupt the input order, that is, insert nodes in random order when building a binary search tree, it is difficult to degenerate into a chain, and the greater probability is a balanced binary tree.

Now we randomly assign A priority to each node, and select nodes to insert into the tree according to the order of priority from high to low. This is the same as randomly disrupting the input order just now. In this way, the binary tree we build is basically balanced. The tree is the tree, the priority is attribute A, and the value of the node is attribute B; Attribute A conforms to the nature of heap and attribute B conforms to the nature of binary lookup tree.

In tree, priority is randomly assigned. It ensures that it will not be excessively unbalanced through randomness, but it can not ensure that it is strictly balanced. Therefore, the tree is a weakly balanced tree.
Look at an example: ordinary balanced tree

Topic description general balanced tree

You need to write a data structure (refer to the title) to maintain some numbers, which needs to provide the following operations:
1. Insert an integer x
2. Delete an integer x (if there are multiple identical numbers, delete only one)
3. Query the ranking of integer x (if there are multiple identical numbers, the smallest ranking will be output). The same numbers will be ranked in turn, not in parallel
4. Query the number ranked as x, and the concept of ranking is the same as 3
5. Find the precursor of X (precursor is defined as the maximum number less than x) to ensure that X has a precursor
6. Find the successor of X (successor is defined as the smallest number greater than x) to ensure that X has successor

Input format

The first line n represents the number of operations (n < = 500000)

Each of the following n lines has two numbers opt and X. opt represents the sequence number of the operation (1 < = opt < = 6, - 10 ^ 7 < = x < = 10 ^ 7)

Large scale input data, establish read in optimization

Output format

For operations 3, 4, 5 and 6, a number is output for each line, indicating the corresponding answer

Data scale

$ 1 \leq n \leq 500000$

Use treap to solve this problem.

node

Nodes are represented by structures, including left and right sons, node values, node priorities, etc
The priority of nodes adopts random number.

struct node{
    int ch[2], val, pri, sz;
}arr[MAXN];

Rotation operation

Rotation operation has a skill. If it is done recursively from top to bottom, it is relatively convenient to take the point above the rotation edge as a parameter.

void rote(int &r, int flg){
    int t = arr[r].ch[1-flg];
    arr[r].ch[1-flg] = arr[t].ch[flg];
    arr[t].ch[flg] = r;
    pushup(r);
    pushup(t);
    r = t;
}

Insert node

The insertion function is similar to the ordinary binary search tree, but it needs to be rotated when the priority of the son is greater than that of the father.

void insert(int &r,  int x){
    if(r == 0){
        arr[++pcnt].val = x, arr[pcnt].pri = rand(), ++arr[pcnt].sz;
        r = pcnt;
        pushup(r);
        return;
    }
    if(x <= arr[r].val) {
        insert(arr[r].ch[0], x);
         if(arr[r].ch[0] && arr[r].pri > arr[arr[r].ch[0]].pri) rote(r, 1); //right tot
    }
    else  {
        insert(arr[r].ch[1], x);
         if(arr[r].ch[1] && arr[r].pri > arr[arr[r].ch[1]].pri) rote(r, 0); // left rot
    }
    pushup(r);
}

Delete operation

The deletion operation is exactly the same as the ordinary binary lookup tree, and there is no need to rotate.
First, recursively find the node to be deleted. After finding it, judge: if the node to be deleted has less than two sons, delete it directly and the son will replace its position; Otherwise, find the largest node in the left subtree (the node must have no right son), and cut the node to replace the node to be deleted.
Here is a place to pay special attention. If there are multiple nodes with the same value in the tree, pay attention to whether the deletion operation Deletes one at a time or all at once.
A better method is to merge multiple nodes with the same value into one node and add an attribute to represent the number of occurrences of the node.

//Here, duplicate nodes are stored in the tree. When deleting, they are replaced one by one from the lower network, and finally one node is guaranteed to be deleted
int del(int &r, int x){
    int tmp;
    if(arr[r].val == x || arr[r].val > x && arr[r].ch[0] == 0 || arr[r].val < x && arr[r].ch[1] == 0){
        if(arr[r].ch[0] == 0 || arr[r].ch[1] == 0) {
            tmp = arr[r].val;
            r = arr[r].ch[0] + arr[r].ch[1];
            return tmp;
        }
        else{
            tmp = arr[r].val; 
            arr[r].val = del(arr[r].ch[0], x);
        }
    }
    else if(x < arr[r].val) tmp = del(arr[r].ch[0], x);
    else tmp = del(arr[r].ch[1], x);
    pushup(r);
    return tmp;
}

Find the x-th element

int xth(int r, int x){
    if(arr[arr[r].ch[0]].sz >= x) return xth(arr[r].ch[0], x);
    else if(arr[arr[r].ch[0]].sz + 1 >= x) return arr[r].val;
    else return xth(arr[r].ch[1], x - arr[arr[r].ch[0]].sz - 1);
}

Ask about x's ranking

int getrank(int r, int x){
    if(r == 0) return 1;
    if(x > arr[r].val) 
    return arr[arr[r].ch[0]].sz + 1 + getrank(arr[r].ch[1], x);
    else return getrank(arr[r].ch[0], x);
}

Find precursors

int getpre(int r, int x){
    if(r == 0) return -MOD;
    if(arr[r].val >= x) return getpre(arr[r].ch[0], x);
    else return max(arr[r].val, getpre(arr[r].ch[1], x));
}

Find successor

int getnxt(int r, int x){
    if(r == 0) return MOD;
    if(arr[r].val <= x)return getnxt(arr[r].ch[1], x);
    else return min(arr[r].val, getnxt(arr[r].ch[0], x));
}

The complete code is as follows:

#include <bits/stdc++.h>
using namespace std;
#define MAXN 1000005
#define MOD 1000000000
struct node{
    int ch[2], val, pri, sz;
}arr[MAXN];
int n, m, opt, x, pcnt, rt;
int cntres;
void pushup(int r){
    if(r) arr[r].sz = arr[arr[r].ch[0]].sz + arr[arr[r].ch[1]].sz + 1;
}
void rote(int &r, int flg){
    int t = arr[r].ch[1-flg];
    arr[r].ch[1-flg] = arr[t].ch[flg];
    arr[t].ch[flg] = r;
    pushup(r);
    pushup(t);
    r = t;
}
void insert(int &r,  int x){
    if(r == 0){
        arr[++pcnt].val = x, arr[pcnt].pri = rand(), ++arr[pcnt].sz;
        r = pcnt;
        pushup(r);
        return;
    }
    if(x <= arr[r].val) {
        insert(arr[r].ch[0], x);
         if(arr[r].ch[0] && arr[r].pri > arr[arr[r].ch[0]].pri) rote(r, 1); //right tot
    }
    else  {
        insert(arr[r].ch[1], x);
         if(arr[r].ch[1] && arr[r].pri > arr[arr[r].ch[1]].pri) rote(r, 0); // left rot
    }
    pushup(r);
}
int del(int &r, int x){
    int tmp;
    if(arr[r].val == x || arr[r].val > x && arr[r].ch[0] == 0 || arr[r].val < x && arr[r].ch[1] == 0){
        if(arr[r].ch[0] == 0 || arr[r].ch[1] == 0) {
            tmp = arr[r].val;
            r = arr[r].ch[0] + arr[r].ch[1];
            return tmp;
        }
        else{
            tmp = arr[r].val;
            arr[r].val = del(arr[r].ch[0], x);
        }
    }
    else if(x < arr[r].val) tmp = del(arr[r].ch[0], x);
    else tmp = del(arr[r].ch[1], x);
    pushup(r);
    return tmp;
}
bool find(int r, int x){
    if(r == 0) return 0;
    if(arr[r].val == x) return 1;
    else if(x < arr[r].val) return find(arr[r].ch[0], x);
    else return find(arr[r].ch[1], x);
}
int xth(int r, int x){
    if(arr[arr[r].ch[0]].sz >= x) return xth(arr[r].ch[0], x);
    else if(arr[arr[r].ch[0]].sz + 1 >= x) return arr[r].val;
    else return xth(arr[r].ch[1], x - arr[arr[r].ch[0]].sz - 1);
}
int getrank(int r, int x){
    if(r == 0) return 1;
    if(x > arr[r].val) return arr[arr[r].ch[0]].sz + 1 + getrank(arr[r].ch[1], x);
    else return getrank(arr[r].ch[0], x);
}
int getpre(int r, int x){
    if(r == 0) return -MOD;
    if(arr[r].val >= x) return getpre(arr[r].ch[0], x);
    else return max(arr[r].val, getpre(arr[r].ch[1], x));
}
int getnxt(int r, int x){
    if(r == 0) return MOD;
    if(arr[r].val <= x)return getnxt(arr[r].ch[1], x);
    else return min(arr[r].val, getnxt(arr[r].ch[0], x));
}
int main(){
    srand(time(0));
    int rescnt = 0, res = 0;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%d %d", &opt, &x);
        if(opt == 1){insert(rt, x); cntres++;}
        else if(opt == 2) { del(rt, x), --cntres;}
        else if(opt == 3) printf("%d\n",getrank(rt, x));  
        else if(opt == 4) printf("%d\n", xth(rt, x));
        else if(opt == 5) printf("%d\n", getpre(rt, x));
        else printf("%d\n", getnxt(rt, x)); 
    }
    return 0;
}

Non rotating heap

Non rotating heap is made of Fan Haoqiang Invented by the boss, it abandons the rotation operation, but uses the split and merge operation as the basic operation to insert and delete nodes while maintaining the order of the binary search tree and the nature of the heap.

As shown in the figure below, this is a tree. The first number in each node is the weight and the second number is the priority.

The weight satisfies the nature of binary search tree, and the priority satisfies the nature of heap.

split operation

Splitting operation is the most difficult operation to understand in non rotating tree. It essentially divides the tree into two trees through one path. To insert or delete a node, we need to find a location to insert or delete the node, so we get a path from the root to the location (there may be only one point on the path).

Take inserting a node with a weight of 20 as an example: first, start from the root and find the corresponding position of the new node, which should be located at the node J J J's right son. So we got one from A A A to J J The path of J breaks all the edges on this path, and points less than or equal to 20 are divided to the left; Points larger than 20 are divided to the right, so two trees are obtained: as shown in the following figure:

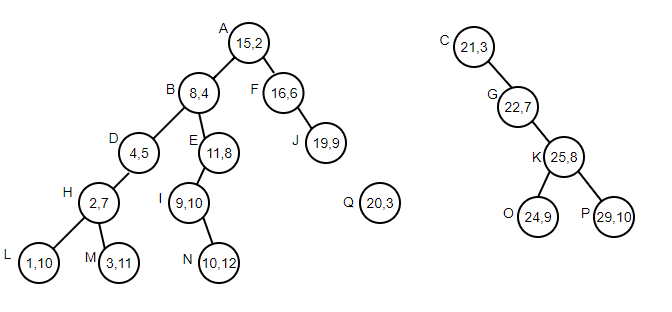
Next, the generated weight is 20 20 20 node Q Q Q. Priority is assumed to be 3 3 3.

Next, we need to use the merge operation merge.

merge operation

The objects of the merge operation are two trees, which must meet the requirements. The maximum weight of the tree on the left is less than the minimum weight of the tree on the right. We merge according to its priority. To describe the aspect, we set the tree on the left as L L 50. The tree on the right is R R R. First, compare the roots of the two trees. The one with the lower priority will be the new root. Suppose L L If the priority of L is small, the problem is converted to L L Right subtree of L and R R The merger of R; Otherwise R R The root of R is used as the root of the new tree, and the problem is transformed into L L L and R . r s o n R.rson R. The merging problem of rson is solved. In this way, the recursion continues until a tree is empty, and the recursion ends.

The merge operation is relatively simple, so it is not shown in the figure above.

Like the code for inserting node Q above, we first merge subtree A and Q, and then continue to merge the merged new tree with subtree C.

The code of deletion operation can also be used s p l i t split split and m e r g e merge merge operation. For example, to delete a weight of x x Node of x.

First, through a split operation, the weight is less than or equal to x x x and weight greater than x x The nodes of x are separated, and then the weight is equal to x x The sum of x is less than x x When x is separated, we get three trees.

If the weight is equal to x x If there is more than one node of x, we can set the weight equal to x x The left and right subtrees of the tree of x are merged, which is equivalent to deleting the root node.

Now there are still three trees. We merge them into one tree from left to right. This completes the deletion task. We need two s p l i t split split and three times m e r g e merge merge operation.

If you want to delete ownership, the value is x x x node, then we only need to do it twice s p l i t split split and once m e r g e merge merge operation

Template problem general balanced tree

Input format

The first line n represents the number of operations (n < = 500000)

Each of the following n lines has two numbers opt and X. opt represents the sequence number of the operation (1 < = opt < = 6, - 10 ^ 7 < = x < = 10 ^ 7)

Large scale input data, establish read in optimization

Output format

For operations 3, 4, 5 and 6, a number is output for each line, indicating the corresponding answer

Data scale

$ 1 \leq n \leq 500000$

Non rotating heap is used to solve this problem

#include <bits/stdc++.h>
using namespace std;
#define MAXN 1000005
#define INF 999999999
int n;
struct node{
    int ch[2], val, pri, sz;
}tree[MAXN];
int rt, root1, root2, tot;
void update(int rt){
    if(rt == 0) return;
    tree[rt].sz = tree[tree[rt].ch[0]].sz + tree[tree[rt].ch[1]].sz + 1;
}
void split(int rt, int &xroot, int &yroot, int v){
    if(rt == 0) xroot = yroot = 0;
    else if(v < tree[rt].val) yroot = rt, split(tree[rt].ch[0], xroot, tree[yroot].ch[0], v);
    else xroot = rt, split(tree[rt].ch[1], tree[xroot].ch[1], yroot, v);
    update(rt);
} 

void merge(int &rt, int xroot, int yroot){
    if(xroot == 0 || yroot == 0) rt = xroot + yroot;
    else if(tree[xroot].pri < tree[yroot].pri){
        rt = xroot;
        merge(tree[rt].ch[1], tree[rt].ch[1], yroot);
    }
    else {
        rt = yroot;
        merge(tree[rt].ch[0], xroot, tree[rt].ch[0]);
    }
    update(rt);
}

void insert(int &rt, int v){
    split(rt, root1, root2, v);
    tree[++tot].val = v, tree[tot].pri = rand(), tree[tot].sz = 1, rt = tot;
    merge(root1, root1, tot);
    merge(rt, root1, root2);
}

void del(int &rt, int v){
    int z;
    split(rt, root1, root2, v);
    split(root1, root1, z, v - 1);
    merge(z, tree[z].ch[0], tree[z].ch[1]);
    merge(rt, root1, z);
    merge(rt, rt, root2);
}

int getxth(int rt, int v){
    if(v <= tree[tree[rt].ch[0]].sz) return getxth(tree[rt].ch[0], v);
    else if(v <= tree[tree[rt].ch[0]].sz + 1) return tree[rt].val;
    else return getxth(tree[rt].ch[1], v - tree[tree[rt].ch[0]].sz - 1);
}

int getrank(int rt, int v){
    if(rt == 0) return 1;
    if(v <= tree[rt].val) return getrank(tree[rt].ch[0], v);
    else return tree[tree[rt].ch[0]].sz + 1 + getrank(tree[rt].ch[1], v);
}

int getpre(int rt, int v){
    if(rt == 0) return -INF;
    if(v <= tree[rt].val) return getpre(tree[rt].ch[0], v);
    else{
        return max(tree[rt].val, getpre(tree[rt].ch[1], v));
    }
}

int getnxt(int rt, int v){
    if(rt == 0) return INF;
    if(v >= tree[rt].val) return getnxt(tree[rt].ch[1], v);
    else return min(tree[rt].val, getnxt(tree[rt].ch[0], v));
}
int main(){
    int opt, x;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%d %d", &opt, &x);
        switch (opt)
        {
        case 1: insert(rt, x); break;
        case 2: del(rt, x); break;
        case 4: printf("%d\n",getxth(rt, x)); break;
        case 3: printf("%d\n",getrank(rt, x)); break;
        case 5: printf("%d\n",getpre(rt, x)); break;
        default: printf("%d\n", getnxt(rt,x)); break;
        }
    } 
}

Keywords: Algorithm data structure

Added by abnfire on Sun, 02 Jan 2022 23:36:15 +0200

Programming VIP

Implementation and application of treap

Implementation and application of tread

concept

Topic description general balanced tree

Input format

Output format

Data scale

node

Rotation operation

Insert node

Delete operation

Find the x-th element

Ask about x's ranking

Find precursors

Find successor

Non rotating heap

split operation

merge operation

Template problem general balanced tree

Input format

Output format

Data scale

Popular Keywords