B-tree is a self balanced multi fork search tree, which is mainly used in disk index.
Here we mainly talk about the implementation, insertion and deletion of B-tree. The definition, principle and application of B-tree are no longer proposed.
Realization of B-number
Before explaining the specific operations, we should first define the B tree and its nodes.
class bnode
{
public:
bnode(int leaf,int m);
~bnode();
int nums;
int leaf;//Is it a leaf node
int *keys;
bnode **children;
};
class btree
{
public:
btree(int m);
void insert(int key);
void del(int key);
bnode *root;
void print();
int m;//Order of b-tree
private:
void _insert(bnode *node,int key);
void split(bnode *node,int n);
void _del(bnode *node,int key);
void merge(bnode *node,int n);
void _print(bnode *node);
};
It is suggested that the order m of B tree should be even, because it is convenient for node splitting in insertion operation. Of course, it is not impossible to select m as an odd number, but when splitting, we should consider the different number of key s in the split node.
Insertion of B-tree
To sum up, there are two steps. One is to find the corresponding node through comparison. The other is to compare the key values on the node, find the appropriate location and insert.
void btree::_insert(bnode *node,int key)
{
int index=node->nums-1;
if(node->leaf==1)//Just plug it in
{
//If you can directly enter this function, you must be dissatisfied with node, so you can insert it safely
while(index>=0&&key<node->keys[index])//Look from right to left because you have to move the original value back
{
node->keys[index+1]=node->keys[index];//Leaf node, no tube node
--index;
}
node->keys[index+1]=key;
++node->nums;
}else//If you are not a leaf node, you need to find it recursively
{
while(index>=0&&key<node->keys[index])//Find from right to left
{
--index;
}
if(node->children[index+1]->nums==m-1)//First judge whether the child to be inserted is full
{
split(node,index+1);
if(key>node->keys[index+1])//After inserting, you need to judge the size of the node
{
++index;
}
}
_insert(node->children[index+1],key);
}
}
void btree::insert(int key)
{
if(root->nums==m-1)//The root node is full
{
bnode *node=new bnode(0,m);//Create a new node as the root node
bnode *r=root;
root=node;
node->children[0]=r;
split(node,0);
if(key>node->keys[0])
{
_insert(root->children[1],key);//Insert right subtree
}else
{
_insert(root->children[0],key);//Insert left
}
}else//The root node is not full
{
_insert(root,key);
}
}
Note here that during the process of finding the corresponding node, if the number of key s of a node is found to be m-1, the node needs to be split at this time.

void btree::split(bnode *node,int n)//n means the number of children at this node will split
{
int t=ceil(m/2);//The minimum number of child nodes and the minimum number of key s of a node should be reduced by -
bnode *child=node->children[n];//Node to split
bnode *x=new bnode(node->children[n]->leaf,m);//The newly split node is at the same level as node
int index=0;
for(index=0;index<t-1;++index)
{
x->keys[index]=child->keys[t+index];
}
if(child->leaf==0)//The child nodes should also be moved
{
for(index=0;index<t;++index)
{
x->children[index]=child->children[m-t+index];
}
}
child->nums=t-1;
x->nums=t-1;
for(index=node->nums;index>=n+1;--index)
{
node->children[index+1]=node->children[index];
}
node->children[n+1]=x;
for(index=node->nums-1;index>=n;--index)
{
node->keys[index+1]=node->keys[index];
}
node->keys[n]=child->keys[m-t-1];
++node->nums;
}
Of course, here is to split and then insert to ensure that after inserting the node, the node can still meet the properties of B-tree. There is another way to judge whether the node meets the splitting condition after insertion. If so, it will split, and the node will not be split in the previous search process.
Deletion of B-tree
To sum up, the deletion of B tree is also a two-step operation. First, recursively find the corresponding subtree. If it is an internal node, judge whether it needs borrowing. Second, judge the situation and delete it.
Here is a separate description of the situation encountered during deletion. After all, deletion is the most difficult part of the whole concept of B-tree.
Here we first give a conclusion that deleting nodes and inserting nodes actually operate on leaf nodes.
Deletion mainly involves two core operations, borrowing and merging. To sum up, there are four situations.
For convenience, let t=ceil(m/2). At this time, t is the minimum number of sub nodes of non root nodes of B tree, and t-1 is the lower limit of the number of key s of non root nodes of B tree.
There are two cases.
Consider the simple case first. If the number of child node key s to be found next is greater than t-1, you can delete them directly without considering the problem of borrowing.
In the second case, the number of child node key s to be found next is equal to t-1. At this time, there are three small cases.
Borrow
There are two small cases.
From the front, it is the left brother of this child node. If the number of key s of this node is greater than t-1, the left brother will borrow. If the left brother is also t-1 or empty, that is, there is no left brother, find the right brother. The picture here only shows the borrowing of the left brother.
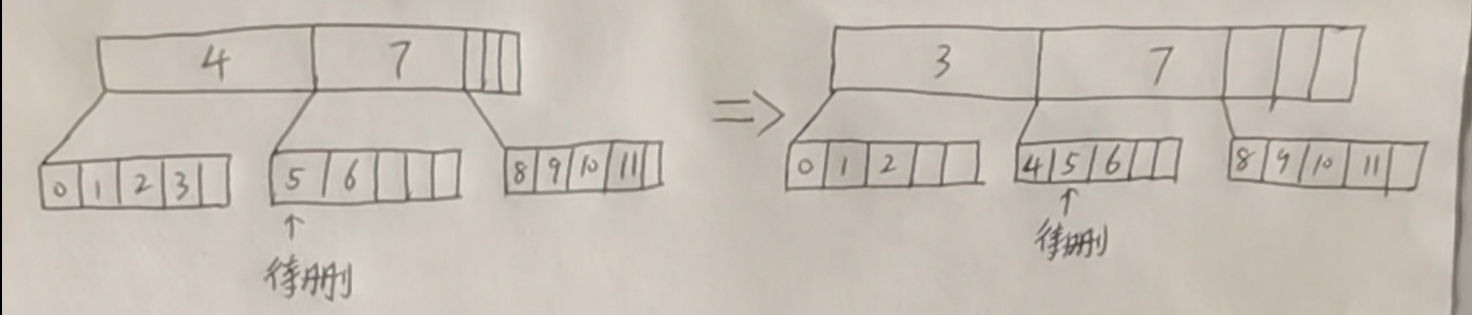
2. Consolidation
At this time, the left and right brother key trees are t-1 or one brother does not exist. Cannot borrow, need to merge.
Only the pictures merged with the left brother are posted here.
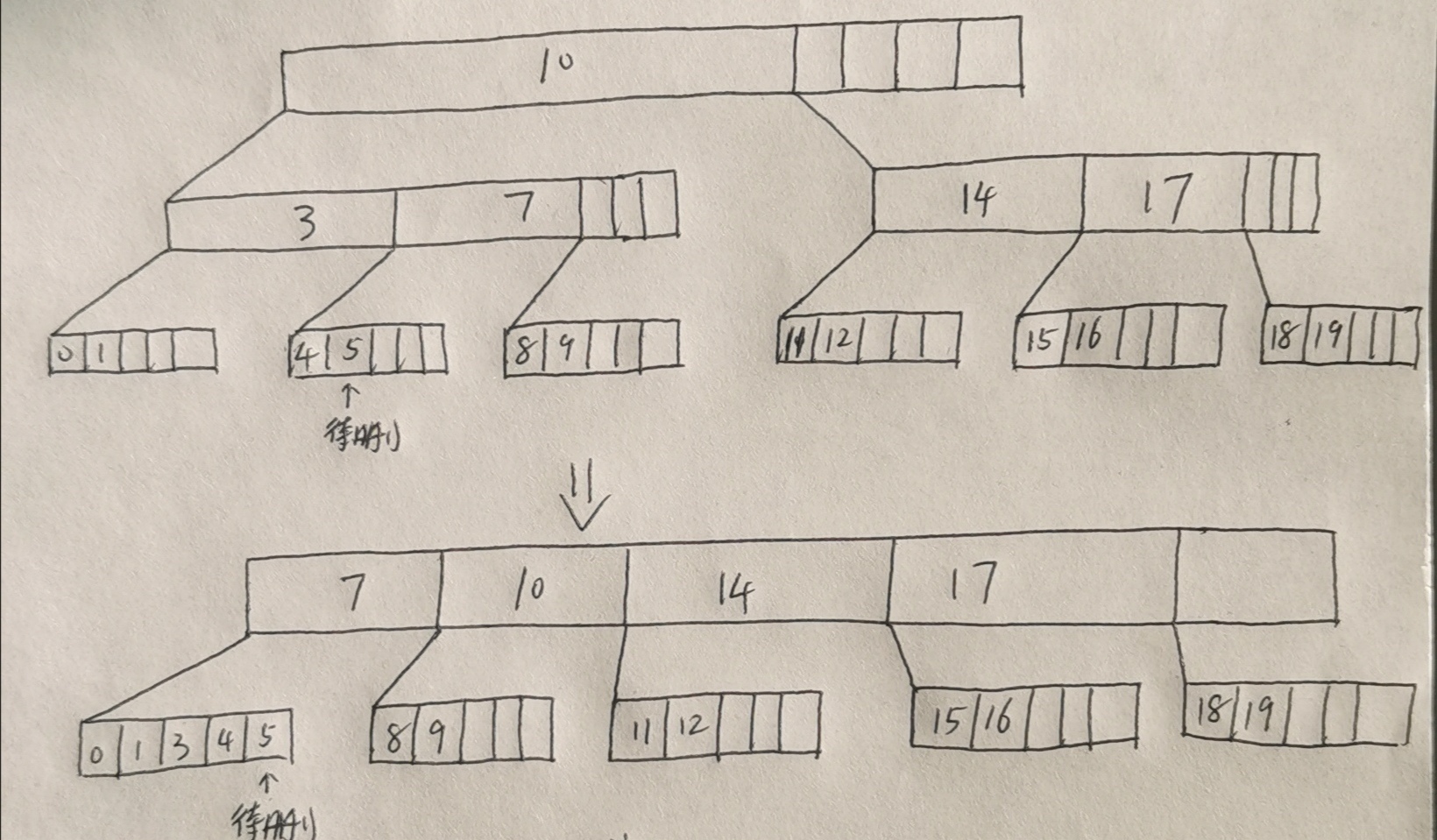
Note that this is the result of two merges. In addition, when deleting a node, judge the situation first and then delete it to ensure that the B-tree still meets the properties after deletion.
void btree::merge(bnode *node,int n)
{
int t=ceil(m/2);
bnode *left=node->children[n];
bnode *right=node->children[n+1];
left->keys[t-1]=node->keys[n];
int i=0;
for(i=0;i<t-1;++i)
{
left->keys[t+i]=right->keys[i];
}
if(left->leaf==0)
{
for(int i=0;i<t;++i)
{
left->children[t+i]=right->children[i];
}
}
left->nums+=t;
delete right;
for(i=n+1;i<node->nums;++i)
{
node->keys[i-1]=node->keys[i];
node->children[i]=node->children[i+1];
}
node->children[i+1]=NULL;
--node->nums;
if(node->nums==0)//Node is the root node
{
delete node;
root=left;
}
}
The code of the whole deletion operation is posted below.
void btree::_del(bnode *node,int key)
{
int t=ceil(m/2);
int i=0,j;
while(i<node->nums&&key>node->keys[i])//Look left to right
{
++i;
}
if(i<node->nums&&key==node->keys[i])//eureka
{
if(node->leaf)//Delete directly. If you can enter here, it means that the node must be enough
{
for(j=i;j<node->nums-1;++j)
{
node->keys[j]=node->keys[j+1];
}
node->keys[j]=0;
--node->nums;
if(node->nums==0)//Node is the root node
{
delete node;
root=NULL;
}
return;
}
//If it is not the root node, you need to take a value from the rich child node to overwrite the value to be deleted
bnode *left=node->children[i];
bnode *right=node->children[i+1];
if(left->nums>t-1)//Left child rich
{
node->keys[i]=left->keys[left->nums-1];
_del(left,left->keys[left->nums-1]);
}else if(left->nums>t-1)//Right child rich
{
node->keys[i]=right->keys[0];
_del(right,right->keys[0]);
}else//Are not rich, then merge
{
merge(node,i);
_del(left,key);
}
}else//There is no such value in the current node. i is the first index greater than key in the node. If it is not greater than key, it is the right boundary
{
bnode *child=node->children[i];//The left child of that node
if(child==NULL)//Think about it. Why not use node - > leaf as the judgment condition here
{
cout<<"cannot find key:"<<key<<endl;
return;
}
if(child->nums==t-1)//You need to borrow a value from the left and right nodes
{
//Note that the meanings of left and right here are different from those above
bnode *left=NULL;//The left neighbor of this child node
bnode *right=NULL;//Right neighbor
if(i>0)//You can't cross the border
{
left=node->children[i-1];
}
if(i<node->nums)
{
right=node->children[i+1];
}
if(left&&left->nums>t-1)
{
for(j=child->nums;j>0;--j)
{
child->keys[j]=child->keys[j-1];
child->children[j+1]=child->children[j];
}
child->children[1]=child->children[0];
child->children[0]=left->children[left->nums];
child->keys[0]=node->keys[i-1];
node->keys[i-1]=left->keys[left->nums-1];
left->keys[left->nums-1]=0;
left->children[left->nums]=NULL;
--left->nums;
}else if(right&&right->nums>t-1)
{
child->keys[child->nums]=node->keys[i];
child->children[child->nums+1]=right->children[0];
++child->nums;
node->keys[i]=right->keys[0];
for(j=0;j<right->nums-1;++j)
{
right->keys[j]=right->keys[j+1];
right->children[j]=right->children[j+1];
}
right->keys[right->nums-1]=0;
right->children[right->nums-1]=right->children[right->nums];
right->children[right->nums]=NULL;
--right->nums;
}else if(left&&left->nums==t-1)//They are not rich and need to be merged
{
merge(node,i-1);
child=left;//Convenient later recursion
}else if(right&&right->nums==t-1)//The left is empty (cross-border), the right is not rich, and the right is merged
{
merge(node,i);
}
}
_del(child,key);
}
}
void btree::del(int key)
{
_del(root,key);
}
Logarithm
Another version of the B-tree code is found here to verify with the logarithm mentioned earlier. Only the code of the logarithm is posted here.
int _compare(bnode *node1,btree_node *node2,bTree *T)
{
int i=0;
int nums1=node1->nums;
int nums2=node2->num;
if(nums1!=nums2)
{
cout << "nums1:" <<nums1<<"nums2:"<<nums2<< endl;
return 1;
}
for(;i<nums1;++i)
{
if(node1->keys[i]!=node2->keys[i])
{
btree_print(T, T->root, 0);
return 1;
}
}
if(node1->leaf)
{
return 0;
}
for(i=0;i<=nums1;++i)
{
if(_compare(node1->children[i],node2->childrens[i],T))
{
return 1;
}
}
return 0;
}
int compare(btree *t,bTree *T)
{
return _compare(t->root,T->root,T);
}
B + tree
Let's briefly mention the B + tree. As a variant of B tree, B + tree mainly solves the problem of low search efficiency of B tree range, because all the values of B + tree exist in the leaf node, the inner node only stores the corresponding index, and the leaf nodes are connected by pointers, which is similar to the structure of linked list. The specific concepts are not posted. Only the code defined by the B + tree is posted here.
class bpnode
{
public:
int nums;
int leaf;//Is it a leaf node
int *keys;
bnode **children;
bnode *leaf_node;//Index to leaf node
};
class list
{
public:
list* prev;
list *next;
bpnode *path;//Corresponding B + tree node
int index;//Which element of the linked list
};
class bptree
{
public:
bnode *root;
int m;//Order of b-tree
list *head;
};
Of course, there are many applications of B + tree. For example, mysql index is realized by B + tree. The code here is not perfect. If you have a chance, continue to implement the B + tree.