1.1 basic concepts
A binary heap is a complete binary tree (different from a full binary tree). The value of a node in the heap is always not greater than the value of its parent node. Usually, this heap is called the maximum heap (the corresponding minimum heap can be defined). An element in the lower layer is not necessarily smaller than an element in the upper layer.
1. Large top reactor (maximum reactor)
The value of any parent node of the maximum heap is greater than or equal to the value of its left and right child nodes.
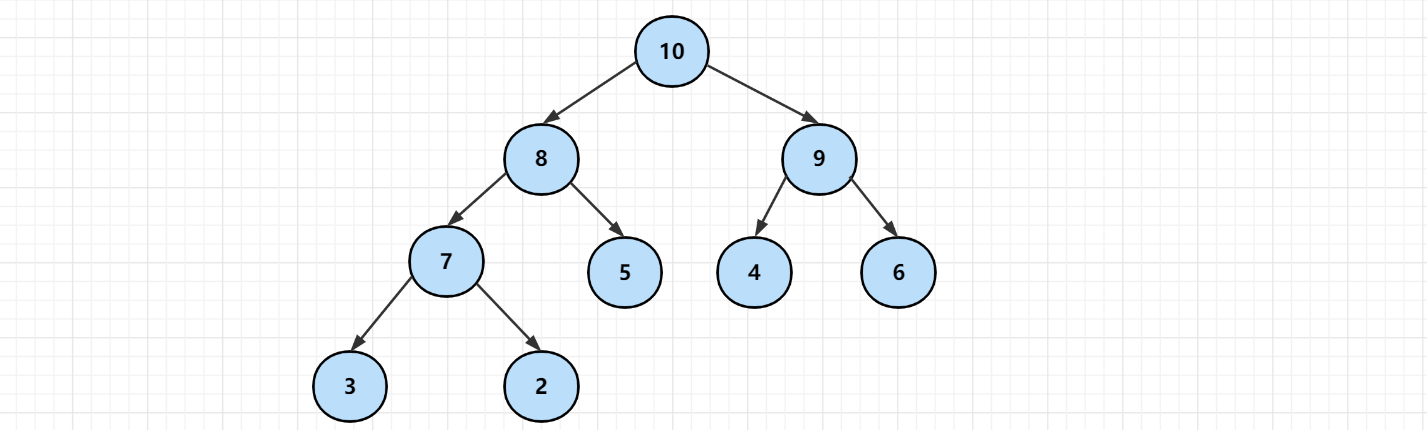
2. Small top pile (minimum pile)
The value of any parent node of the minimum heap is less than or equal to the value of its left and right child nodes.
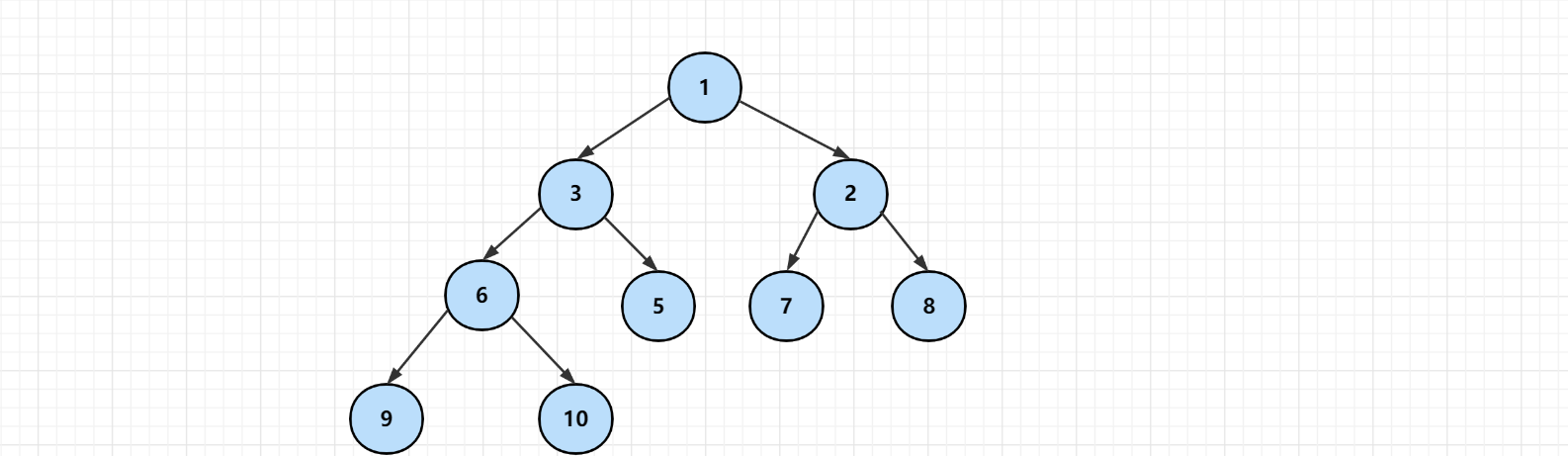
The root node of a binary heap is called the top of the heap
The characteristics of the maximum heap and the minimum heap determine that the top of the maximum heap is the largest element in the whole heap, and the top of the minimum heap is the smallest element in the whole heap.
1.2 storage principle
A complete binary tree is more suitable for storing arrays. Using an array to store a complete binary tree is very memory saving. Because we do not need to store the pointers of the left and right child nodes, we can find the left and right child nodes and parent nodes of a node simply through the subscript of the array.
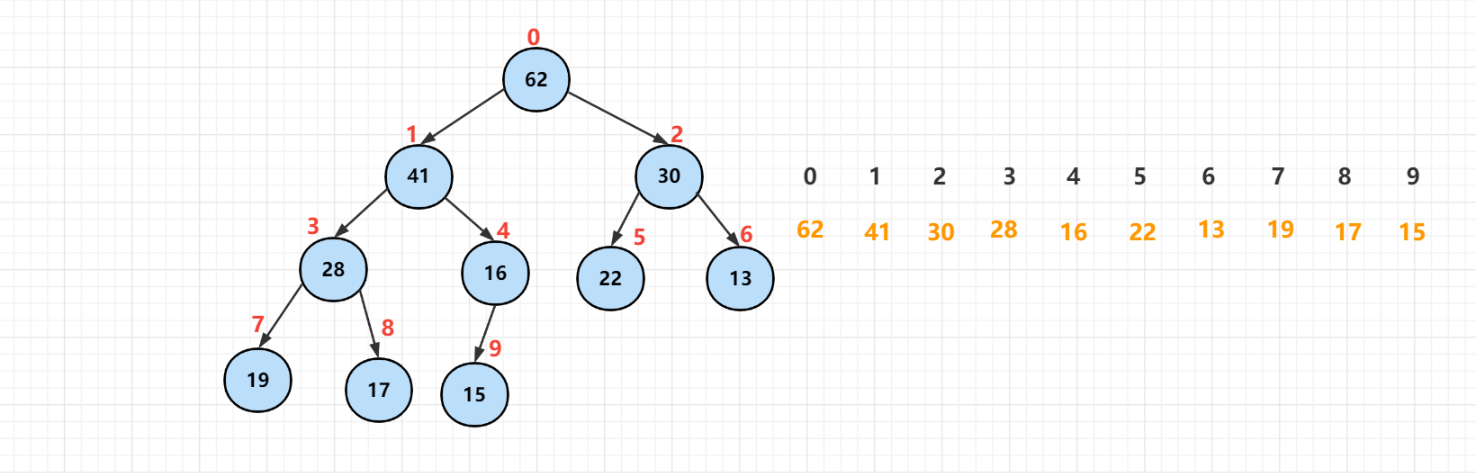
We can see from the figure that the left child node of the node with subscript i in the array is the node with subscript left child(i) = i * 2 + 1, the right child node is the node with subscript right child(i) = i * 2 + 2, and the parent node is the node with subscript parent(i) = (i-1) /2.
1.3 train of thought analysis
1. Add element
The elements in the heap are arranged in the style of array. Adding elements is equivalent to the rightmost element of the sequence traversal, that is, the rightmost element of the lowest layer. From the perspective of array representation, the value of element [52] is added at the position with index [10].
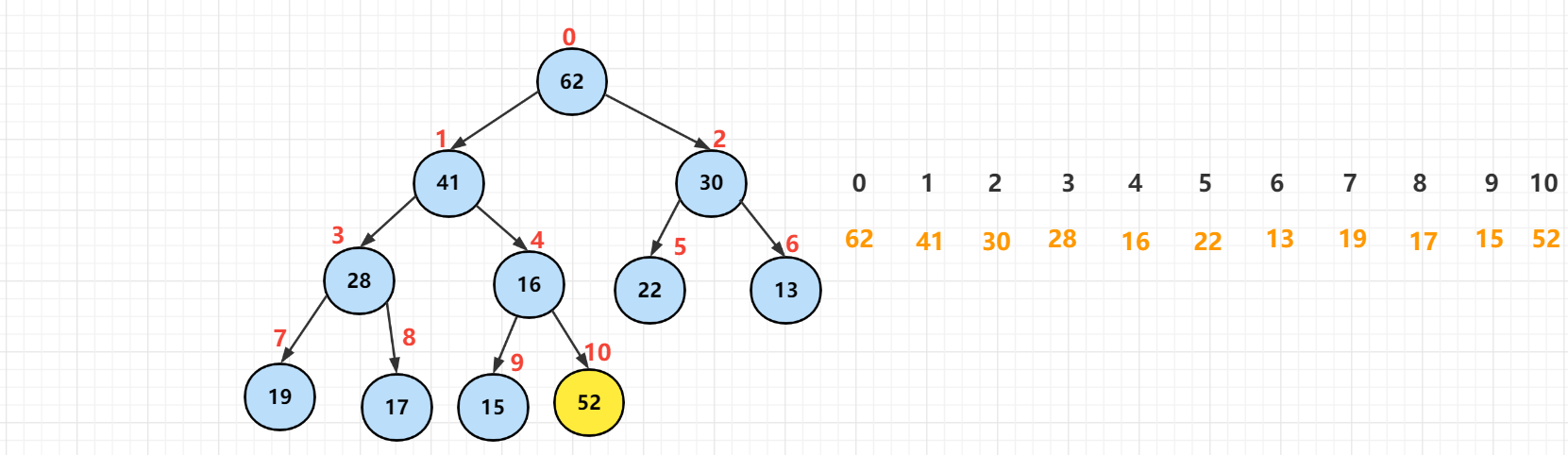
This obviously does not meet the nature of the heap. All the added elements are compared with the parent node. It is found that element [52] is larger than [16], so the positions of the two elements need to be exchanged.
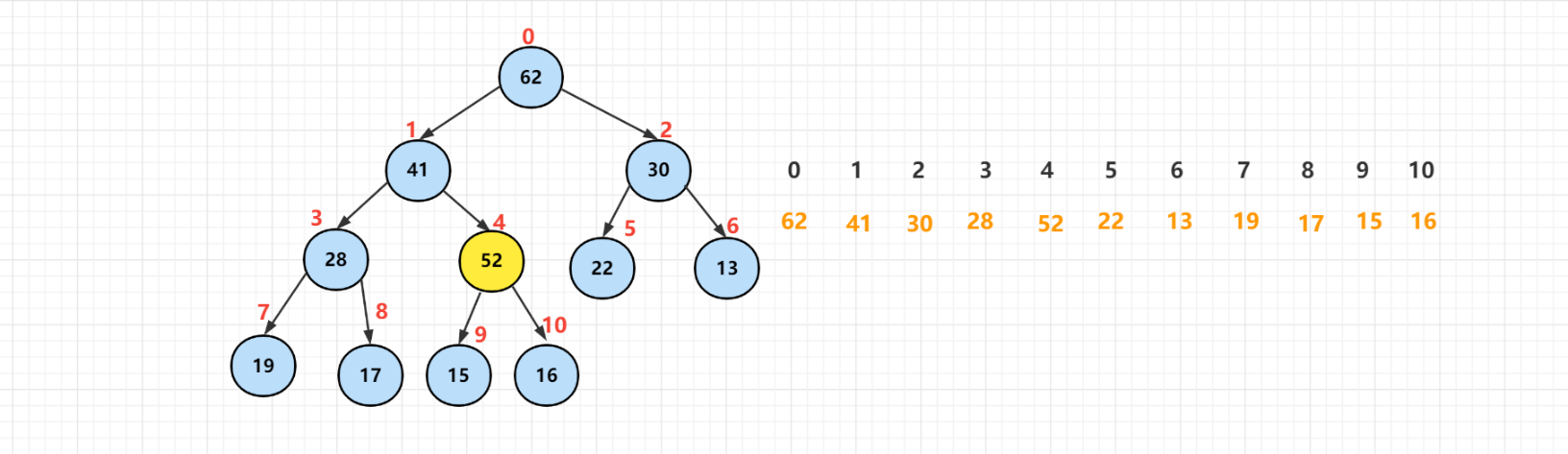
The binary tree with [52] as the root satisfies the nature of heap, but this is obviously not enough. The node [52] is larger than its parent node [41], so there is also element exchange between the two.
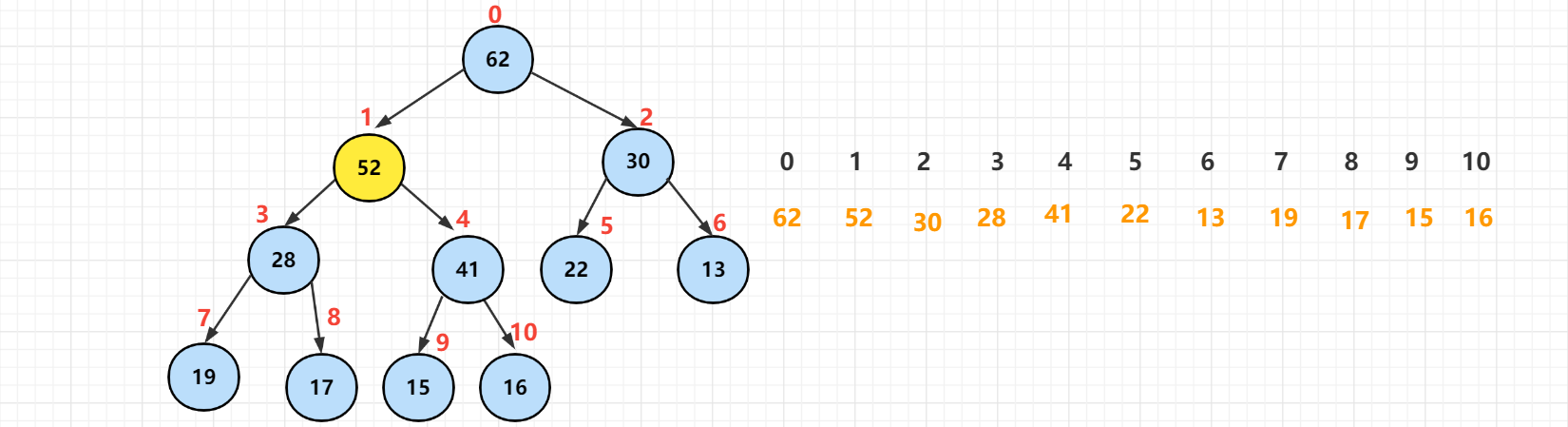
At this time, [52] is smaller than the element node [62], which meets the nature of the heap. Therefore, the nature of the heap is not destroyed at this position.
2. Delete element
Take out the elements from the heap, only the largest element, the top element, and the top element.
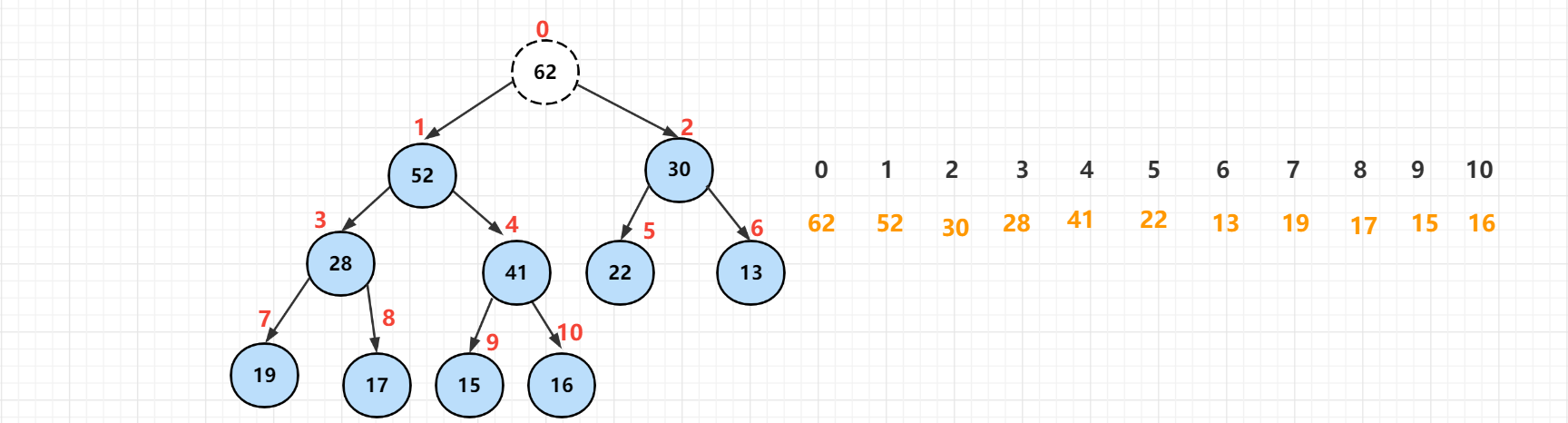
Top the last element [16] in the heap to the top of the heap. After this operation, the element with index 0 is [16], and the last element is also 16. Then delete the last element. One element is successfully reduced from the number of elements, and it is the element at the top of the heap.
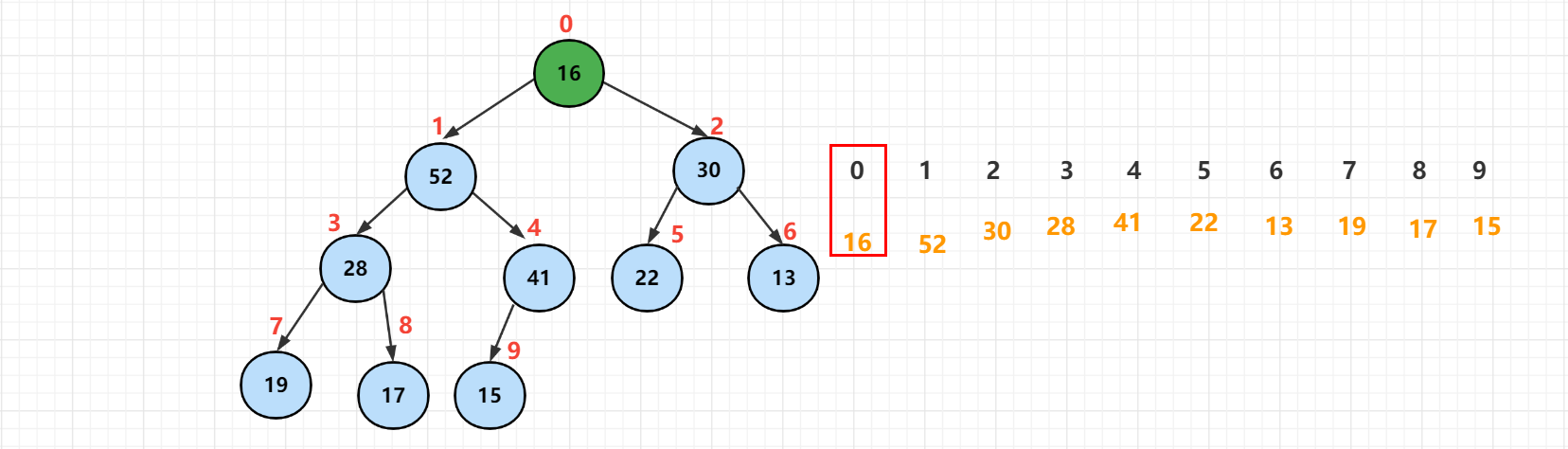
However, now that the elements at the top of the heap have broken the nature of the heap, the sinking operation should be performed to compare the sinking elements with its left and right children. Select the largest element in the child. If it is smaller than the largest element, exchange it.
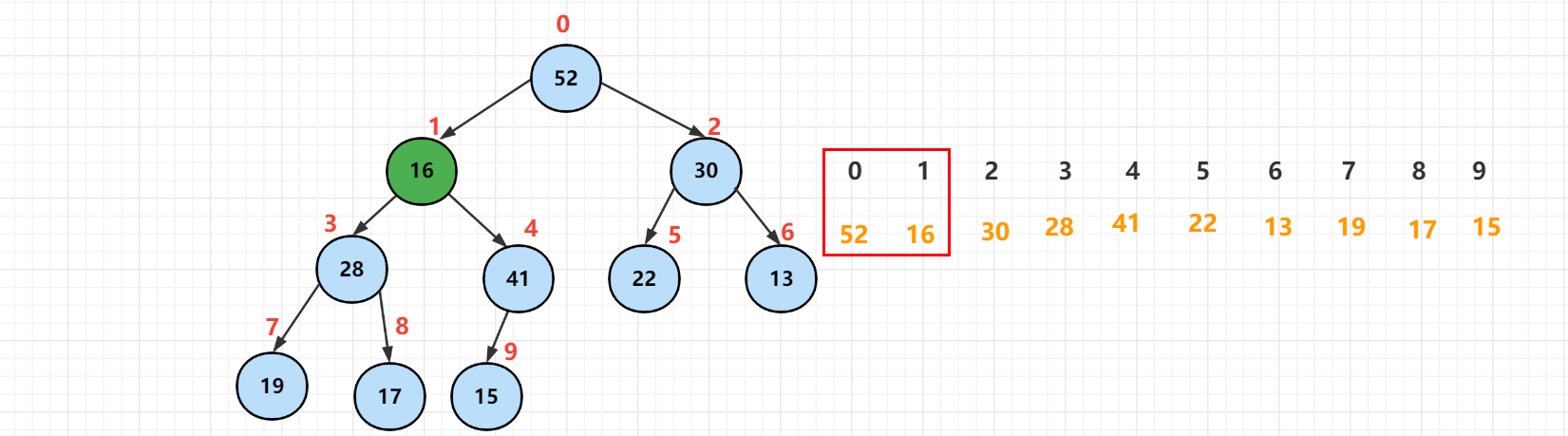
Then continue to compare and exchange.
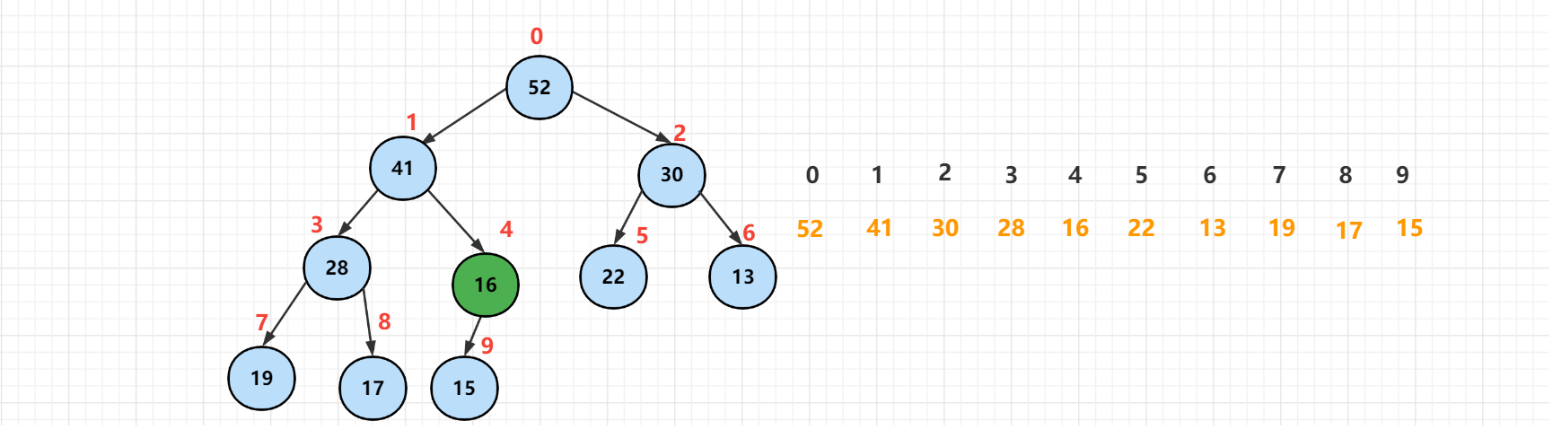
At this time, the sinking node is larger than 15, which meets the basic properties of the heap. At this time, the sinking operation has ended.
1.4 code implementation
1. Sequence table: ArrayList
package cn.heap.demo01;
import java.util.Iterator;
public class ArrayList<E> implements Iterable<E>{
// Elements of the sequence table
private E[] data;
// Number of sequential table elements
private int size;
// Define constants
private static final int ELEMENT_NOT_FOUND = -1;
private static final int DEFAULT_CAPACITY = 6;
// Number of elements
public int size() {
return size;
}
//Clear all elements
public void clear() {
for (int i = 0; i < size; i++) {
data[i] = null;
}
size = 0;
}
// Constructor, passing in the capacity of the array to construct SqList
public ArrayList(int capacity){
data = (E[]) new Object[capacity];
capacity = (capacity < DEFAULT_CAPACITY) ? DEFAULT_CAPACITY : capacity;
}
// Parameterless constructor. The capacity of the default array is capacity=10
public ArrayList(){
this(DEFAULT_CAPACITY);
}
// Gets the capacity of the array
public int getCapacity(){
return data.length;
}
// Gets the number of elements in the array
public int getSize(){
return size;
}
// Returns whether the array is empty
public boolean isEmpty(){
return size == 0;
}
// Add a new element after all elements
public void addLast(E e){
add(size, e);
}
// Add a new element before all elements
public void addFirst(E e){
add(0, e);
}
// Insert a new element at the index e
public void add(int index, E e){
// Capacity expansion operation
if(size == data.length){
resize(2 * data.length);
}
for(int i = size - 1; i >= index ; i --){
data[i + 1] = data[i];
}
data[index] = e;
size ++;
}
// Gets the element at the index position
public E get(int index){
rangeCheck(index);
return data[index];
}
// View the index of the element
public int indexOf(E e){
if (e == null) {
for (int i = 0; i < size; i++) {
if (data[i] == null) return i;
}
} else {
for (int i = 0; i < size; i++) {
if (e.equals(data[i])) return i;
}
}
return ELEMENT_NOT_FOUND;
}
// Modify the element of index position to e
public void set(int index, E e){
rangeCheck(index);
data[index] = e;
}
// Find whether there is an element e in the array
public boolean contains(E e){
return indexOf(e) != ELEMENT_NOT_FOUND;
}
// Find the index of element e in the array. If element e does not exist, return - 1
public int find(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return i;
}
return -1;
}
// Delete the element at index position from the array and return the deleted element
public E remove(int index){
rangeCheck(index);
E ret = data[index];
for(int i = index + 1 ; i < size ; i ++){
data[i - 1] = data[i];
}
// Empty
data[--size] = null;
// Volume reduction operation
if(size == data.length / 4){
resize(data.length / 2);
}
return ret;
}
// Deletes the first element from the array and returns the deleted element
public E removeFirst(){
return remove(0);
}
// Deletes the last element from the array and returns the deleted element
public E removeLast(){
return remove(size - 1);
}
// Remove element e from array
public void removeElement(E e){
int index = find(e);
if(index != -1) {
remove(index);
}
}
// Array index out of bounds processing
private void outOfBounds(int index){
throw new IndexOutOfBoundsException("index:" + index + ", Size:" + size);
}
// Index value check range method
private void rangeCheck(int index){
if(index < 0 || index >=size){
// Call out of bounds processing method
outOfBounds(index);
}
}
// Add method index check scope
private void rangeCheckAdd(int index){
if(index < 0 || index >size){
// Call out of bounds processing method
outOfBounds(index);
}
}
// capacity expansion method
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity];
for(int i = 0 ; i < size ; i ++){
newData[i] = data[i];
}
data = newData;
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Sequence table(ArrayList)length:%d, container:%d\n", size, data.length));
res.append('[');
for(int i = 0 ; i < size ; i ++){
res.append(data[i]);
if(i != size - 1)
res.append(", ");
}
res.append(']');
return res.toString();
}
// Exchange method
public void swap(int i, int j){
E temp = data[i];
data[i] = data[j];
data[j] = temp;
}
// traversal method
@Override
public Iterator<E> iterator() {
return new SIterator();
}
private class SIterator implements Iterator{
// Define a pointer variable
private int cur;
public SIterator(){
this.cur=0;
}
@Override
public boolean hasNext() {
return cur< size;
}
@Override
public E next() {
return data[cur++];
}
}
}
2. Maximum heap: MaxHeap
package cn.heap.demo01;
import java.util.Iterator;
/***
* Maximum heap implementation
* @param <E>
*/
public class MaxHeap<E extends Comparable<E>> implements Iterable<E>{
// Use ArrayList as the storage container for the largest heap
private ArrayList<E> data;
// Heap space
public MaxHeap(){
data = new ArrayList<>();
}
// Gets the index of the parent node
private int parent(int k){
if(k <= 0){
throw new IllegalArgumentException("No parent node!");
}
return (k -1 ) / 2;
}
// Gets the index of the left child node
private int leftChild(int k){
return 2 * k + 1;
}
// Gets the index of the right child node
private int rightChild(int k){
return 2 * k + 2;
}
// Returns the maximum number of valid heap elements
public int size(){
return data.size();
}
// Determine whether the binary heap is empty
public boolean isEmpty(){
return data.isEmpty();
}
// Empty binary stack
public void clear(){
data.clear();
}
// Add an element to the maximum heap e
public void add(E e){
data.addLast(e);
// Index corresponding to floating element
siftUp(data.size() -1);
}
// Float up the element corresponding to the corner mark K
private void siftUp(int k){
// If the parent node is smaller than itself, exchange elements
while (k > 0 && data.get(k).compareTo(data.get(parent(k))) < 0){
data.swap(k, parent(k));
k = parent(k);
}
}
// Maximum heap found
public E findMax(){
if (data.isEmpty()){
throw new IllegalArgumentException("The maximum heap is empty!!!!");
}
return data.get(0);
}
// Minimum heap
public E findMin(){
if(data.isEmpty()){
throw new IllegalArgumentException("The maximum heap is empty!!!");
}
E min = data.get(0);
for (int i=1; i< data.size(); i++){
if(data.get(i).compareTo(min) < 0){
min = data.get(i);
}
}
// Return minimum heap
return min;
}
// Delete maximum
public E extractMax(){
// Get the maximum
E max = findMax();
// Swap the index 0 with the last element
data.swap(0, data.size() - 1);
// Delete the last element
data.remove(data.size() - 1);
// Call function
siftDown(0);
return max;
}
// float downward
private void siftDown(int k) {
while (leftChild(k) < data.size()){
// Get the maximum value of left and right children
int j = leftChild(k);
if(j + 1 < data.size() && data.get(j+1).compareTo(data.get(j)) > 0){
// data[j] is the maximum of leftChild and rightChild
j = rightChild(k);
}
if(data.get(k).compareTo(data.get(j)) < 0){
data.swap(k,j);
k = j;
}else {
break;
}
}
}
// After taking out the largest element, put in a new element
public E replace(E e){
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
@Override
public Iterator<E> iterator() {
return data.iterator();
}
@Override
public String toString(){
return data.toString();
}
}
3. Test class: TestMaxHeap
package cn.heap.demo01;
import java.util.Random;
public class TestMaxHeap {
public static void main(String[] args) {
MaxHeap<Integer> heap = new MaxHeap<>();
Random random = new Random();
// Traverse add
for (int i=0; i<10; i++){
heap.add(random.nextInt(20));
}
System.out.println(heap);
for (int i=0; i<4; i++){
System.out.println(heap.extractMax());
}
}
}
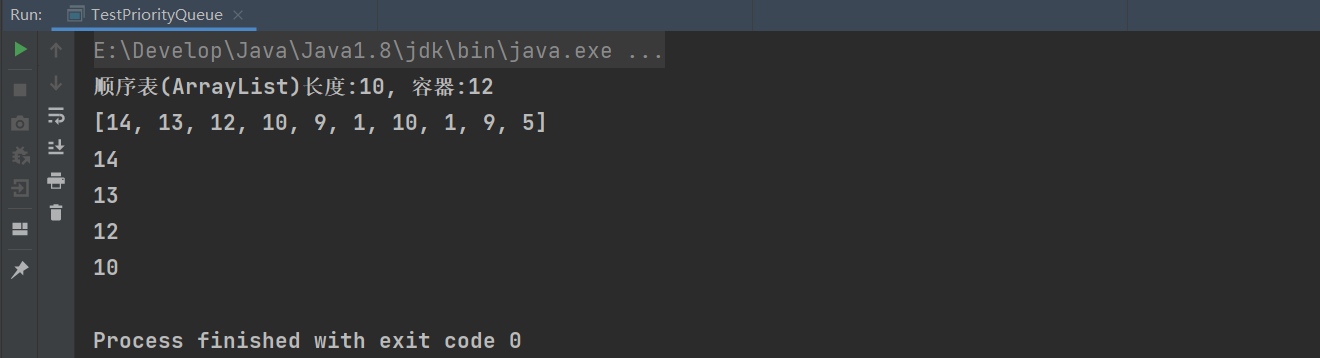
4. Execution results
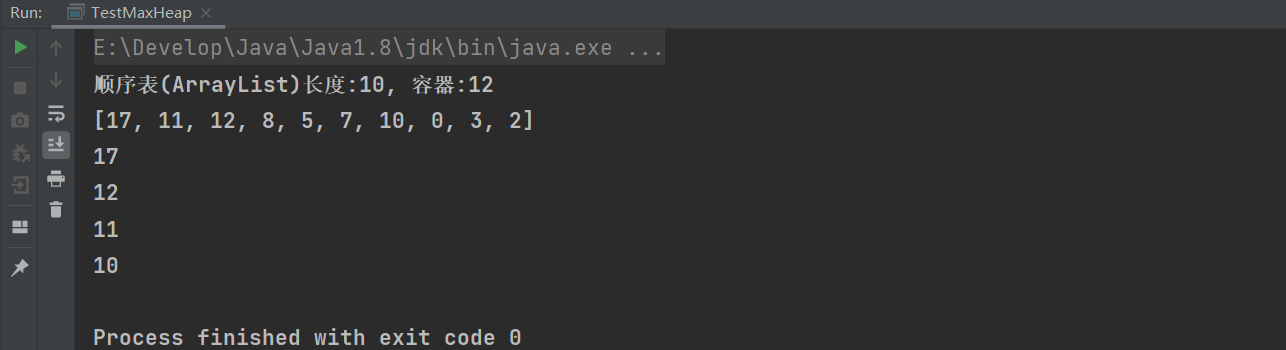
1.5 priority queue
1. Basic introduction
Ordinary queue: first in first out, last in and last out.
Priority queue: the order of leaving the queue has nothing to do with the order of entering the queue. It is related to priority. It is still a queue in essence.
Application: in the task manager: dynamically select the task with the highest priority for execution. In the game: Tower Defense gives priority to attack (distance, threat, order).
2. Case realization
Interface: Queue
package cn.heap.demo02;
public interface Queue<E> extends Iterable<E>{
int size();
boolean isEmpty();
// Queue operation
void enqueue(E element);
// Out of line operation
E dequeue();
// View the elements of the current team leader
E getFront();
// Empty queue
void clear();
}
Priority queue: PriorityQueue
package cn.heap.demo02;
import java.util.Iterator;
public class PriorityQueue<E extends Comparable<E>> implements Queue<E>{
// Heap object
private MaxHeap<E> heap;
// constructor
public PriorityQueue(){
heap = new MaxHeap<>();
}
@Override
public int size() {
return heap.size();
}
@Override
public boolean isEmpty() {
return heap.isEmpty();
}
@Override
public void enqueue(E element) {
// Queue operation
heap.add(element);
}
@Override
public E dequeue() {
return heap.extractMax();
}
@Override
public E getFront() {
return heap.findMax();
}
@Override
public void clear() {
heap.clear();
}
@Override
public Iterator<E> iterator() {
return heap.iterator();
}
@Override
public String toString() {
return heap.toString();
}
}
Test class: TestPriorityQueue
package cn.heap.demo02;
import java.util.Random;
public class TestPriorityQueue {
public static void main(String[] args) {
PriorityQueue<Integer> queue = new PriorityQueue<>();
Random random = new Random();
// Traverse add
for (int i=0; i<10; i++){
queue.enqueue(random.nextInt(20));
}
System.out.println(queue);
for (int i=0; i<4; i++){
System.out.println(queue.dequeue());
}
}
}
results of enforcement