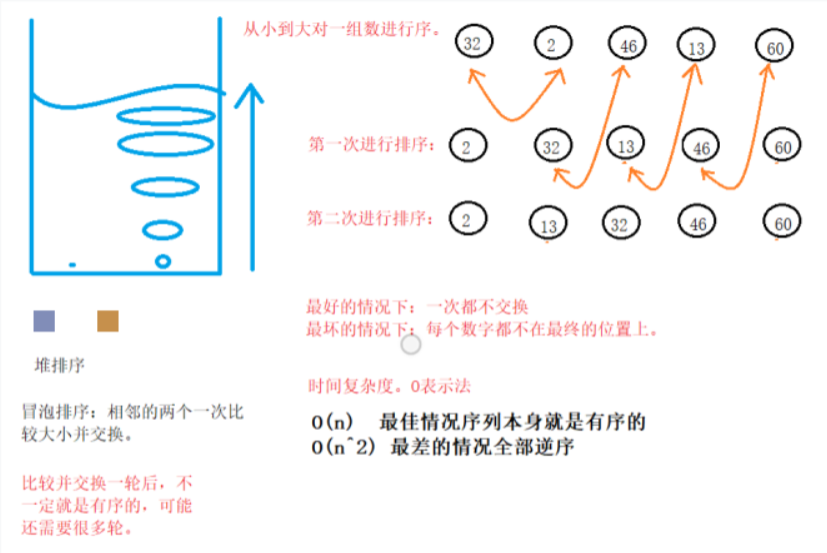
Bubble sort: bubble sort exchanges the elements in reverse order in the pairwise comparison of each trip. Each time, two adjacent elements are compared, and the exchange also occurs between the two elements. Therefore, if two elements are equal, they will not be exchanged again; If two equal elements are not adjacent, even if they are adjacent through the previous pairwise exchange, they will not be exchanged at this time, so the sequence of the same elements has not changed. Therefore, bubble sorting is a stable sorting algorithm, and the final position of at least one value is established in each trip, because this form is like underwater bubbles, and large bubbles always rise upward, So it's called bubble sort.

Implementation of bubble sorting algorithm:

Bubble sort the given array

public class MaoPaoSort {
    public static void main(String[] args) {
        int[] arr={11,23,40,13,42,34,60,1,41};
        System.out.println("===================This is the array before sorting======================");
        printarr(arr);
        System.out.println("===================This is the bubble sorted array===================");
        maopao(arr);
        printarr(arr);
    }
//Write a method to implement bubble sorting
    public static int[] maopao(int[] arr){
        int temp=0;
//The inner loop controls the number of times to sort, and the outer loop controls the number of times adjacent numbers are exchanged in pairs
        for (int i= 0;i<arr.length;i++){
            for (int j=0;j< arr.length-i-1;j++){
//Here, because bubble sorting will determine a maximum value every time
 So internal circulation j The variable subtracts a value every time it loops

                if (arr[j]>arr[j+1]){
                    temp=arr[j];
                    arr[j]=arr[j+1];
                    arr[j+1]=temp;
                }
            }
        }
        return arr;
    }
//Write another method to output the array
    public static int[] printarr(int[] arr){
        for (int i =0;i<= arr.length-1;i++){
            if (i==0){
                System.out.print("["+arr[0]+",");
            }else if (i==arr.length-1){
                System.out.print(arr[arr.length-1]+"]");
            }else{
                System.out.print(arr[i]+",");
            }
        }
        System.out.println();
        return  arr;
    }

Results achieved:

Binary search:

Binary Search is also called half search. Baidu Encyclopedia's description of Binary Search is as follows: Binary Search is also called Binary Search, which is an efficient search method. However, the half search requires that the linear table must adopt the sequential storage structure, and the elements in the table are arranged in order by keywords. Obviously, Binary Search must be used in an ordered structure.

Baidu Encyclopedia's use of binary search: first, assuming that the elements in the table are arranged in ascending order, compare the keywords recorded in the middle of the table with the search keywords. If the two are equal, the search is successful; Otherwise, the middle location record is used to divide the table into the first and second sub tables. If the keyword of the middle location record is greater than the search keyword, the previous sub table will be further searched, otherwise the next sub table will be further searched. Repeat the above process until you find a record that meets the conditions to make the search successful, or until the sub table does not exist, the search is unsuccessful.

Then, knowing the principle and application process of binary search, our specific code implementation is very clear. Binary search can be implemented in java using loop structure or recursive call of method.

The first is the loop structure. Because we don't know the number of loops, we use the while loop to implement it:

import java.util.Scanner;
//Binary search to find the data in the array;
public class Text3Demo6 {
    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11};
   //Keyboard entry creation object
        Scanner sc= new Scanner(System.in);
        System.out.println("Please enter the element you want to find:");
        int num1= sc.nextInt();

   //Set the array header variable to be the first element of the array, and the tail variable to be the last element of the array

        int low = 0;
        int high = arr.length - 1;
        if (num1<arr[0] |num1>arr[arr.length-1]){
            System.out.println("The number of lookups is not in the array");
        }else{
            while (low <= high) {
    //Set an intermediate variable i to be the middle of the head and tail
    //Pay attention to the changes of the head and tail variables after comparing the middle variables with the search number
                int i = (low + high) / 2;
                if (num1 == arr[i]) {
                    System.out.println(i);
                    break;
                } else if (num1 < arr[i]) {
                    high = i - 1;
                } else {
                    low = i + 1;
                }
            }
        }
        if (low > high) {
            System.out.println("The element found is not in the array");
        }
    }}

It can be clearly seen in the code that when the element in the middle of the array is larger than the element we want to find, we need to further find the element on the left of the middle position, so we assign the position of the tail variable to the middle position minus one. When the element in the middle position is smaller than the element we want to find, we need to further find the element on the right of the middle position, so we need to assign the position of the header variable to the middle position plus one, and the loop continues. When we find the element we want, we will output the position i of the element, and end the loop through break. When we don't find the element, It will prompt that the element is not in the array.

When we use methods to implement binary search, we only need to write one implementation of binary search into a method, and then call the method recursively through the return value of the method until the element is found or the condition of the method is not met.

import java.util.Scanner;

public class Text3Demo8 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.println("Please enter a number to find");
        int value= sc.nextInt();
        int[] nums={1,2,3,5,7,8,9,11};
        int flag = erFen(nums,0,7,value);
        System.out.println(flag);
    }
    public static int erFen(int[] nums, int low, int high, int value) {

        if (low > high) 
        return -1;
        // Find the middle subscript
        int mid = low + ((high - low) / 2);
        if (nums[mid] == value) {
            return mid;
        } else if (nums[mid] > value) {
            return erFen(nums, low, mid - 1, value);
        } else {
            return erFen(nums, mid + 1, high, value);
        }

    }}

Finally, the results of a failed search element and a successful search element are placed respectively