1, Merge sort

(1) Top down merge sort

1. Train of thought

It's still easy to understand

• Split a number to be sorted into two arrays.
• Then, the array on the left is recursively merged, and finally an ordered array on the left is obtained [it is also internally split into two small arrays for sorting and merging].
• Then, the array on the right side is recursively merged, and finally an ordered array on the right side is obtained [it is also internally split into two small arrays for sorting and merging].
• Finally, merge the two arrays.

2. Code implementation

Code reading suggestions

• First, look at the merge method in the merge class and understand its meaning
• Take a look at the implementation of all sorting methods in Merge as a whole
• Finally, go to the test

import java.util.Arrays;

public class MergeSort {
    public static void main(String[] args) {
        String[] a = {"A","E","B","D","M"};
        Merge merge = new Merge();
        merge.sort(a);
        System.out.println(Arrays.toString(a));
	
    }

}

class Merge {
    private static Comparable[] aux;

    public static void sort(Comparable[] a) {
        aux = new Comparable[a.length];
        sort(a,0,a.length-1);
    }

    private static void sort(Comparable[] a, int lo, int hi) {
        if (hi <= lo) {
            return;
        }
        int mid = (lo + hi) / 2;
        sort(a,lo,mid);//Like left recursion
        sort(a,mid + 1,hi);//Recursion to the right
        merge(a,lo,mid,hi);//Merge
    }

    public static void merge(Comparable[] a,int lo,int mid,int hi) {
        int i = lo;
        int j = mid + 1;
        for (int k = lo; k <= hi; k++) {
            aux[k] = a[k];
        }
        for (int k = lo; k <= hi; k++) {
            if (i > mid) {//If the left is exhausted
                a[k] = aux[j++];
            } else if (j > hi) {//If the right is exhausted
                a[k] = aux[i++];
            } else if (less(aux[j],aux[i])){//If the element to the left of the current point is larger than the edge element
                a[k] = aux[j++];
            } else {//If the element on the right of the current point is larger than the element on the left
                a[k] = aux[i++];
            }
        }
    }


    //This method is judged and returns true if V < W
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }

    private static void exch(Comparable[] a,int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
}

3. Time complexity and flow chart

• Derivation of time complexity
  The time complexity is 1/2N lgN to N lgN comparisons [see the derivation process below for details]
  
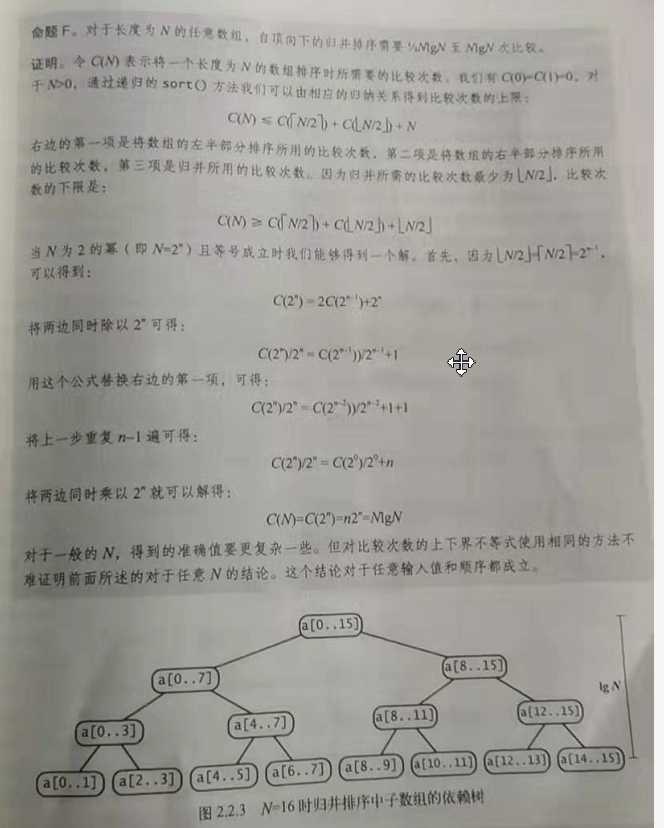
• flow chart
  

4. Test the performance

(1) No improved version test

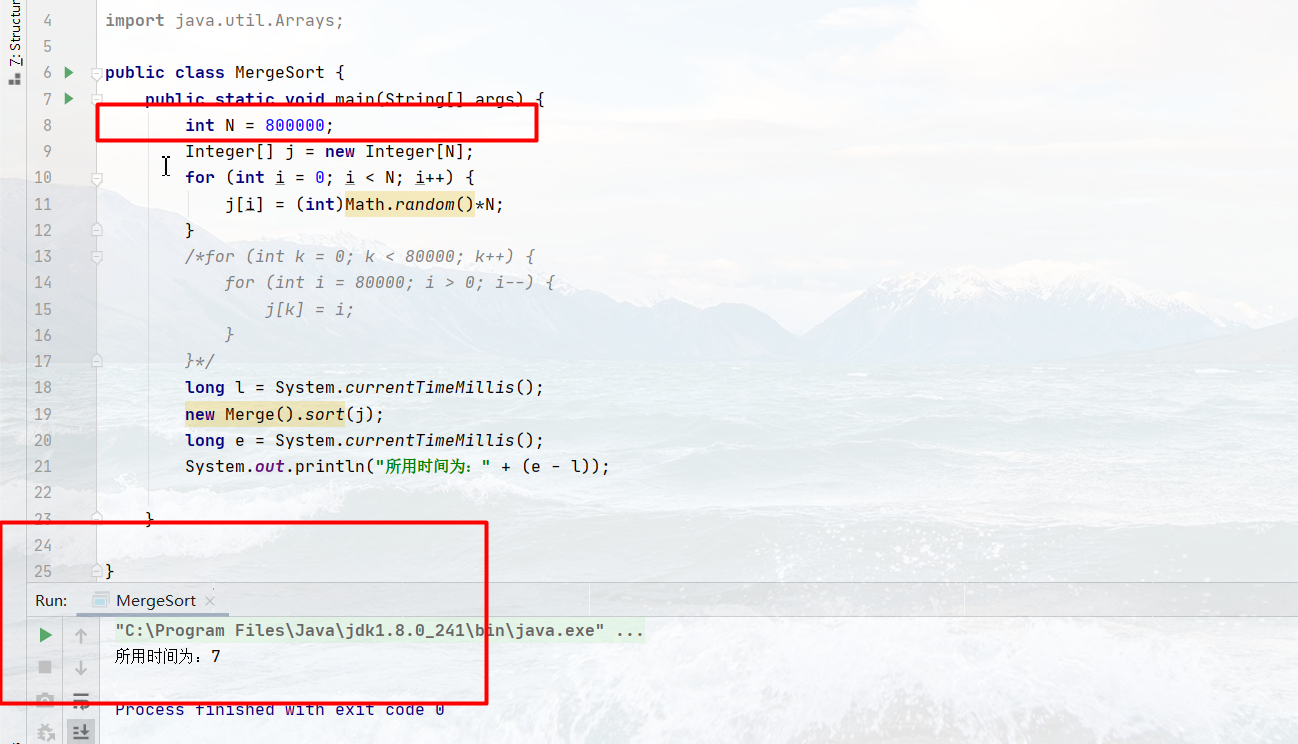
Its performance is no better than our previous two algorithms. This is much better, so increase the data.

public static void main(String[] args) {
        int N = 800000;
        Integer[] j = new Integer[N];
        for (int i = 0; i < N; i++) {
            j[i] = (int)Math.random()*N;
        }
        /*for (int k = 0; k < 80000; k++) {
            for (int i = 80000; i > 0; i--) {
                j[k] = i;
            }
        }*/
        long l = System.currentTimeMillis();
        new Merge().sort(j);
        long e = System.currentTimeMillis();
        System.out.println("The time taken is:" + (e - l));

    }

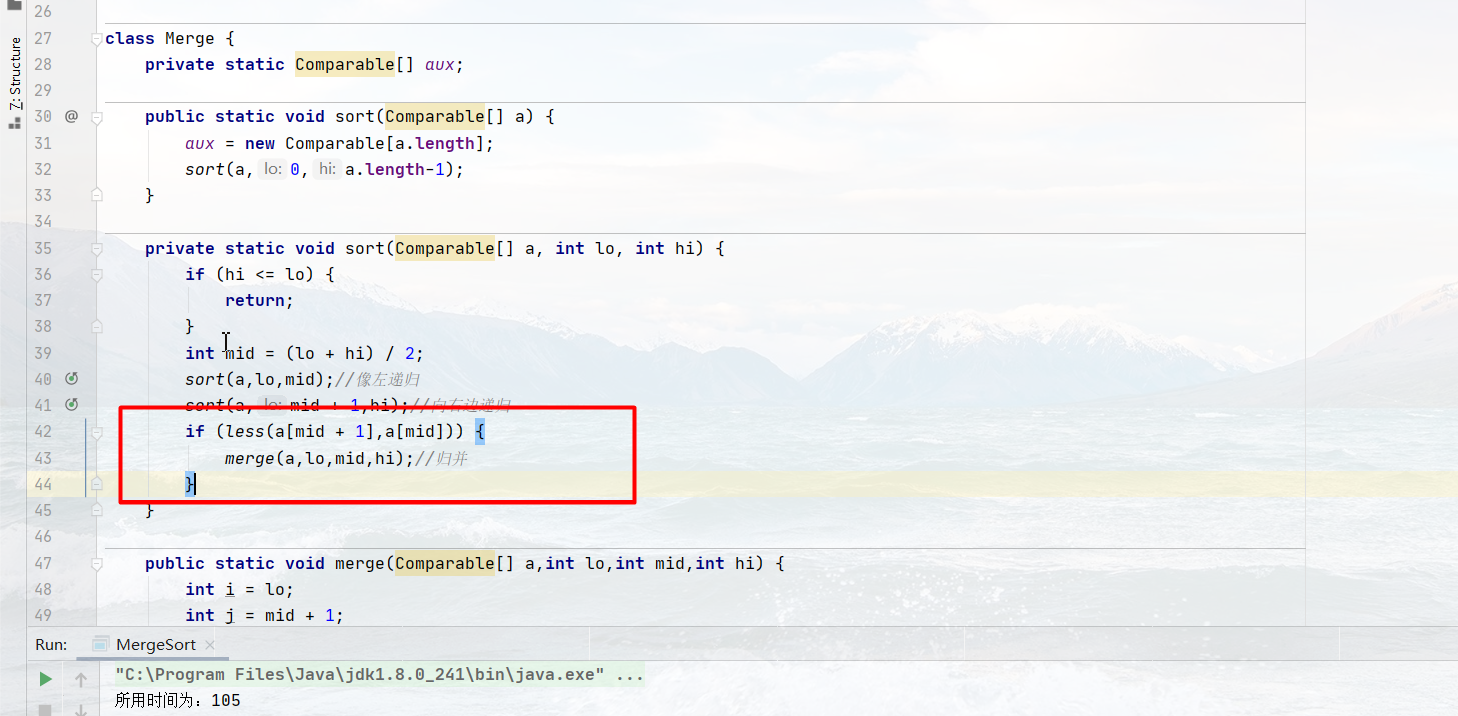
(2) Improved version test

A judgment is made in this method [one recursion is omitted]

private static void sort(Comparable[] a, int lo, int hi) {
        if (hi <= lo) {
            return;
        }
        int mid = (lo + hi) / 2;
        sort(a,lo,mid);//Like left recursion
        sort(a,mid + 1,hi);//Recursion to the right
        if (less(a[mid + 1],a[mid])) {
            merge(a,lo,mid,hi);//Merge
        }
    }

(2) Bottom up merging

1. Thought realization

Look at my analysis

• First of all, we have to understand the top-down design idea above. It first decomposes the large array into two, and then divides the sub array into two. Recursion.
• The bottom-up is to merge and sort two elements, then merge and sort four data, then merge eight, then 18, and so on. Finally, only two elements are merged.
• In addition, you can try it yourself.

2. Code implementation

class MergeBu {
    private static Comparable[] aux;


    public static void sort(Comparable[] a) {
        int N = a.length;
        aux = new Comparable[N];
        for (int sz = 1; sz < N; sz = sz + sz) {
            for (int lo = 0; lo < N - sz; lo += sz + sz) {
                merge(a,lo,lo+sz + 1,Math.min(lo+sz+sz-1,N-1));
            }
        }
    }

    public static void merge(Comparable[] a,int lo,int mid,int hi) {
        int i = lo;
        int j = mid + 1;
        for (int k = lo; k <= hi; k++) {
            aux[k] = a[k];
        }
        for (int k = lo; k <= hi; k++) {
            if (i > mid) {//If the left is exhausted
                a[k] = aux[j++];
            } else if (j > hi) {//If the right is exhausted
                a[k] = aux[i++];
            } else if (less(aux[j],aux[i])){//If the element to the left of the current point is larger than the edge element
                a[k] = aux[j++];
            } else {//If the element on the right of the current point is larger than the element on the left
                a[k] = aux[i++];
            }
        }
    }


    //This method is judged and returns true if V < W
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }

    private static void exch(Comparable[] a,int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

}