1. Introduction to Mandelbrot & Julia set
Mandelbrot set is named after its discoverer mathematician Benoit Mandelbrot. It is a fractal set. In mathematics, fractal is a subset of Euclidean space, and its Hausdorff dimension strictly exceeds the topological dimension. Fractals tend to maintain their form at different levels, which leads to their ubiquity in nature. Fractal is called self similar, which means that they show similar patterns on smaller and smaller scales and are similar to one or more parts of it. Fractal images are usually computer-generated color complex patterns. Because fractal is a set of complex numbers, a formula is needed to calculate the numbers in the fractal set. The mandelbert set is generated. By using the complex quadratic polynomial C, which is a complex parameter, the sequence value generated from z = 0 iteration will gradually diverge to positive infinity or recursively converge to a point according to the equation. Different function values can be generated by using different iterations.
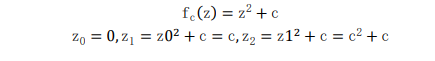
Because the calculation of each point is independent of other points, generating Mandelbrot set is very suitable for parallel calculation. Parallel computing is a process of using multiple computing resources to solve a problem concurrently. In other words, it is an effective method to improve computer processing power and speed. Message passing interface (MPI) is a practical, flexible and efficient standard for generating parallel programs based on message passing. The parallelization of Mandelbrot set is realized by using MPI Library in C programming. A partition scheme based on round robin segmentation is adopted to divide the row into sub rows, and different logical processors are allocated to the sub rows to improve the calculation efficiency of sub rows. Analyze the results and draw a diagram to observe the scalability of the algorithm when the number of logical processors increases.
2. Preliminary analysis
2.1 theoretical parallelism of Mandelbrot sets
A reliable way to detect the parallelism of sequential algorithms is to find out whether the equations of the algorithm can be executed independently of each other. Bernstein conditions can be used here (because they can be exchanged without modifying the program results). The three conditions that make up Bernstein are as follows: 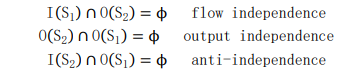
This shows that S1 and S2 can be equal in parallel, and these conditions are expressed in different granularity. As long as these three conditions are satisfied, we can draw the conclusion that the processes are independent of each other and prove that they have great parallelism.
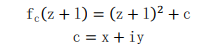
The above formula represents the function calculation of two continuous values of Mandelbrot set. So,
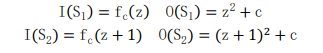
Then the Bernstein condition is applied to obtain the following three equations:
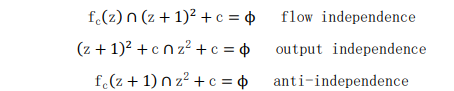
The above equation shows the proof of Bernstein condition. Therefore, both processes S1 and S2 can be executed in parallel, that is (S1 | S2). Therefore, the proof and evidence show that Mandelbrot set can use MPI library for parallel computing in C programming. Similarly, Julia sets also have this parallelism, which will not be repeated here.
2.2 operation logic of Mandelbrot set and Julia set
The pseudo code of Mandelbrot set is as follows:
for each pixel (Px, Py) on the screen do x0 := scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.00, 0.47)) y0 := scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1.12, 1.12)) x := 0.0 y := 0.0 iteration := 0 max_iteration := 1000 while (x*x + y*y ≤ 2*2 AND iteration < max_iteration) do xtemp := x*x - y*y + x0 y := 2*x*y + y0 x := xtemp iteration := iteration + 1 color := palette[iteration] plot(Px, Py, color)
The pseudo code of Julia set is as follows:
R = escape radius # choose R > 0 such that R**2 - R >= sqrt(cx**2 +
cy**2)
for each pixel (x, y) on the screen, do:
{
zx = scaled x coordinate of pixel # (scale to be between -R and
R)
# zx represents the real part of z.
zy = scaled y coordinate of pixel # (scale to be between -R and
R)
# zy represents the imaginary part of z.
iteration = 0
max_iteration = 1000
while (zx * zx + zy * zy < R**2 AND iteration < max_iteration)
{
xtemp = zx * zx - zy * zy
zy = 2 * zx * zy + cy
zx = xtemp + cx
iteration = iteration + 1
}
if (iteration == max_iteration)
return black;
else
return iteration;
}
2.3 explore the influence of parameter C on the shape of Julia set
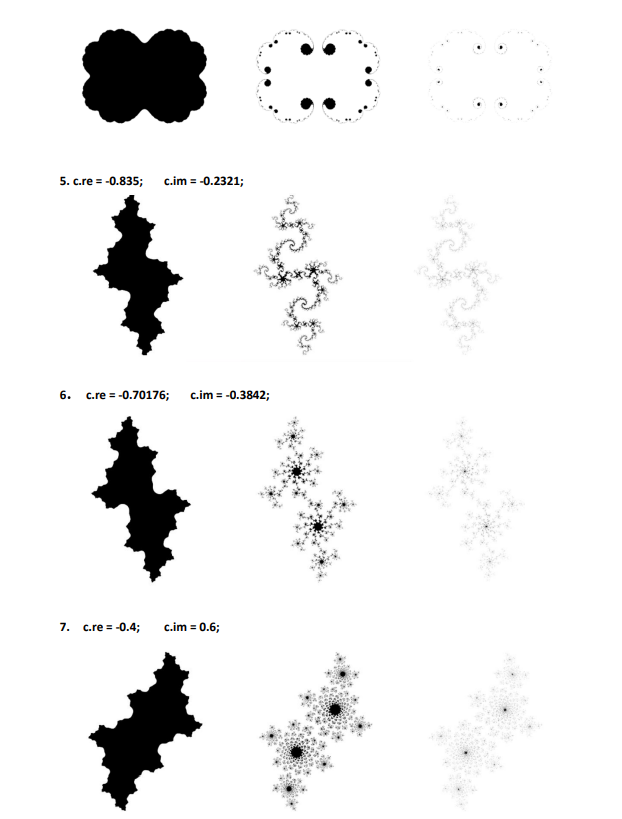
Julia Set is a graph generated by z = z^2+c iteration, fix C, and then calculate the value of divergent Z to obtain the divergent sequence. By changing the value of complex C and then iterating, different Julia graphs can be generated. The following experiments mainly explore the influence of C value on the shape of Julia Set. Seven groups of experiments are designed. Each group has different c.re and c.im, representing the real part and imaginary part of complex C respectively. There are three experiments in each group, and the number of iterations is continuously increased from left to right. It can be observed that the more iterations, the finer the fractal pattern.


3. Zoning scheme design
In order to parallelize sequential algorithms, we need to find operations that can be performed independently of each other, which is where Bernstein's conditions are used. From the running pseudo code of Mandelbrot set and Julia set in Section 2.2, it can be seen that the amount of computation is mainly concentrated in the iteration of for loop, and each iteration process is independent of each other, that is, parallel computing can be carried out. Therefore, we can consider using partition scheme to run in parallel on multi-core computers.
3.1 partition scheme based on polling line segmentation
In this scheme, the root node becomes the master node, performs receive and write operations in parallel, and provides the same amount of work to all available logical processors to collect and send to the master node to generate Mandelbrot Set. The number of rows allocated by each process is the maximum number of rows of the picture pixel matrix divided by the number of processes. The mathematical expression is as follows:
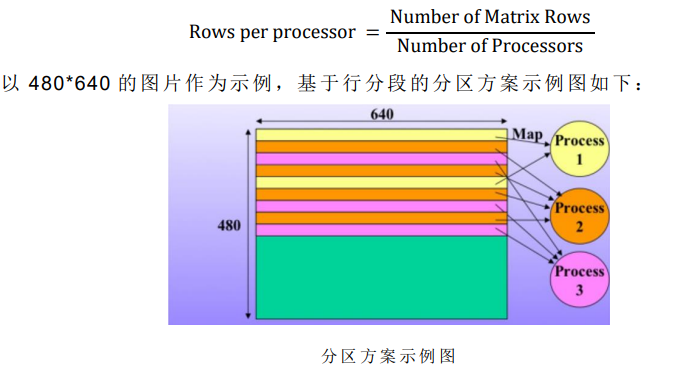
After dividing all the rows, each process sends the generated child rows back to the root node. After receiving all the child rows from all processors, the master node finally writes the Mandelbrot Set image that complies with the algorithm ppm file.
3.2 parallel computing based on MPI
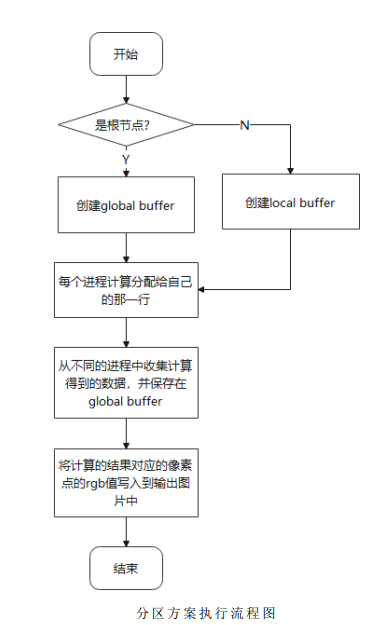
Based on the above partition strategy, mandelbrot's calculation can be assigned to a series of complete and independent tasks to execute respectively. Each node corresponds to a task, that is, calculate the value of the row pixel to which it is assigned. The programming idea of MPI is adopted for program design, and the master can be responsible for the assign task and collection task, while other slave process es perform relevant operations on the corresponding calculation work by obtaining the data partition. The flow chart of its main program code is as follows:
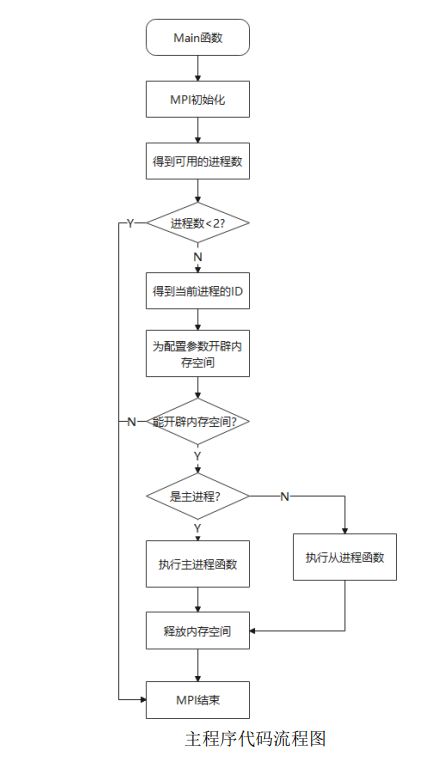
4. Graphic beautification design
4.1 coloring scheme
An image can be regarded as a matrix composed of pixels. Each value on the matrix is rgb, which reflects the color state of the pixel. Therefore, the divergence velocity of each point in Mandelbrot Set and Julia Set can be mapped to an rgb value. Therefore, Mandelbrot and Julia sequences can be visually displayed. The coloring results are as follows:

4.2 other schemes
mandelbrot set is obtained by iterating c continuously when z=0, so we can only get a gourd like picture. However, you can zoom and pan the picture, increase the number of iterations, and change the color mapping relationship to get a more colorful picture. Based on this, parameters that can be configured by users are added to the code of mandelbrot. The specific meanings are shown in the table below
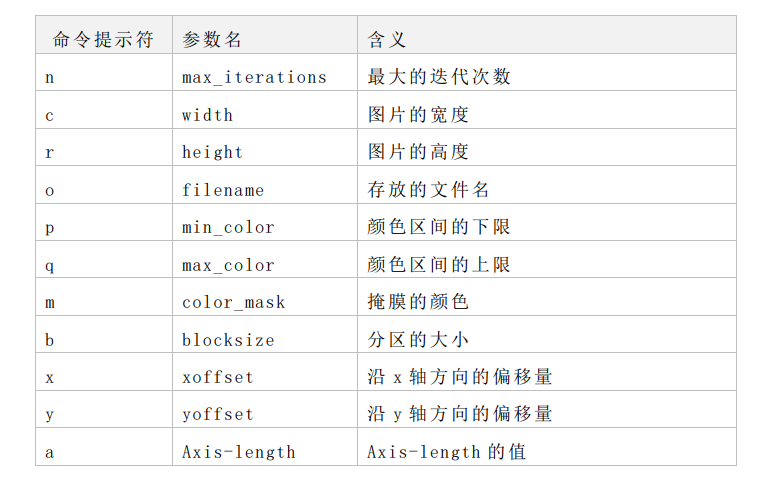
-
Picture flip
Execute the command mpirun - NP 4/ mandelbrot -n 20000 -a -3.5

-
Zoom of picture
Execute the command mpirun - NP 4/ mandelbrot -n 20000 -a 1

-
Change partition size
Execute the command mpirun - NP 4/ mandelbrot -n 5000 -b 8 -a -2

-
Translate along the X,Y axes
Execute the command mpirun - NP 4/ mandelbrot -n 20000 -x 0.1 -y -0.8 -a 0.3

-
Change color range
Execute the command mpirun - NP 4/ mandelbrot -n 10000 -p 0xffffff -q 0x000000

-
Add mask color
Execute the command mpirun - NP 4/ mandelbrot -n 10000 -p 0xffffff -q 0x00cccc -m CCFFFF

5. Results and discussion
Experimental platform:
Hardware: Huawei Kunpeng 920
Software: Xshell, Xftp
Hardware platform parameters
- Cpu information:
Enter the command "lscpu" to view the cpu information. You can see that the name of the model is
KunPeng-920 has 64 CPUs in total, and each core corresponds to one thread.
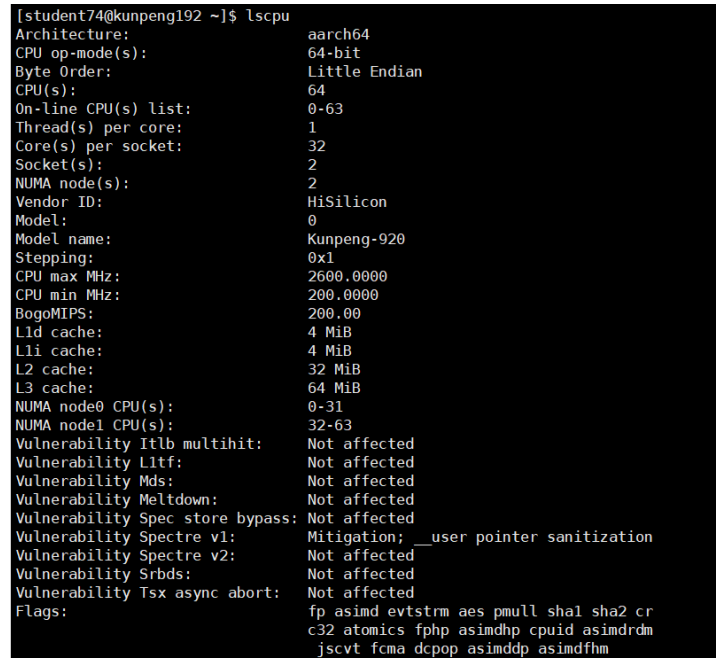
- Number of logical CPUs: 64

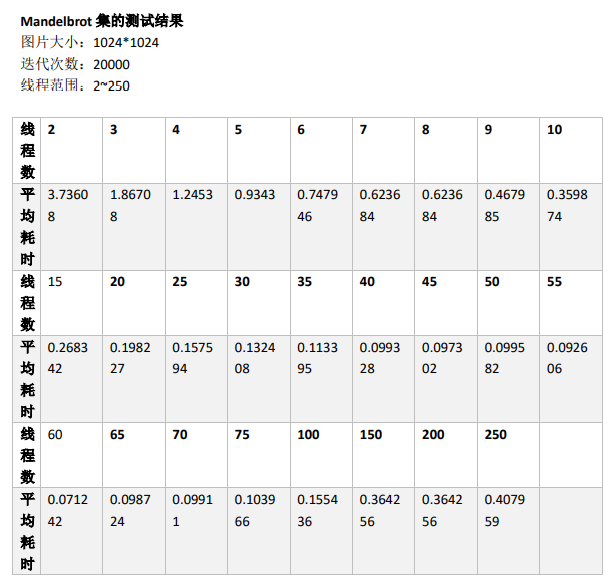
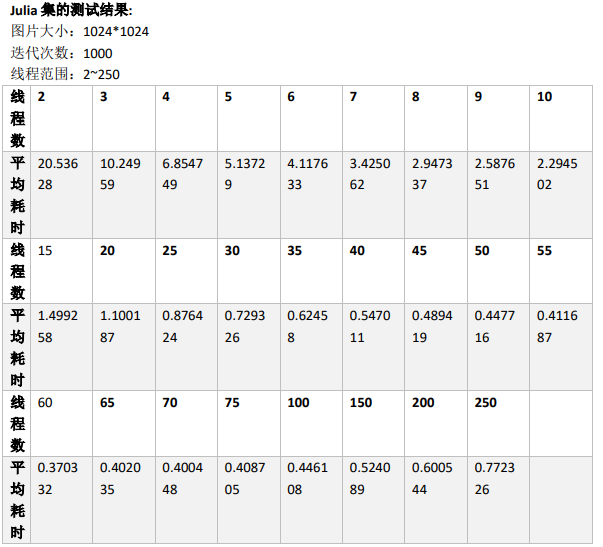
Test scheme: 26 groups of experiments are set for each fractal, and each group of experiments is equipped with different threads, ranging from 2 to 250. Each group of experiments is repeated for 5 times to obtain the average value of its time-consuming (see the appendix for specific values)
Visual analysis: draw a broken line diagram of the relationship between the number of threads and time consumption of Mandelbrot and Julia respectively.
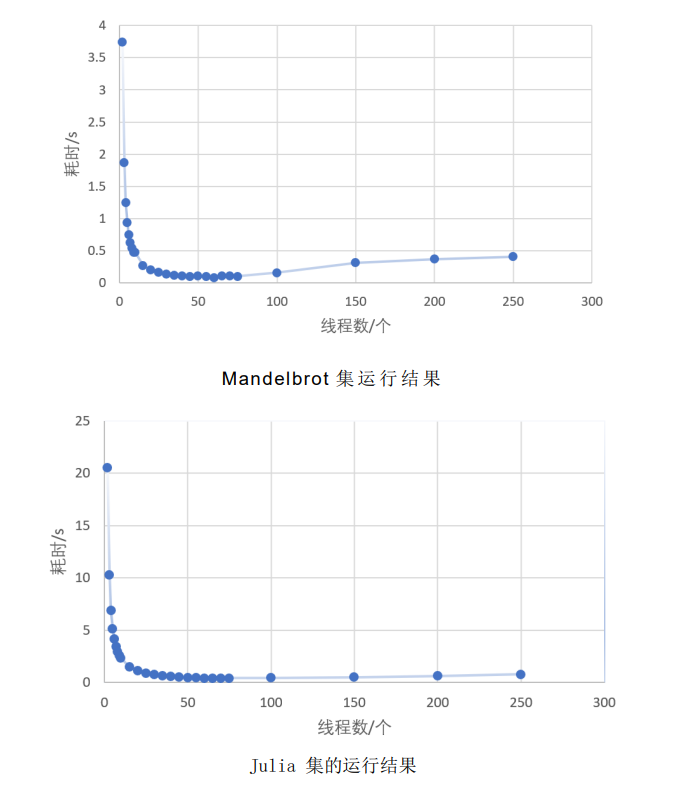
As can be seen from the above table, the number of threads ranges from 2 to 25. With the increase of the number of threads, the time consumption decreases rapidly;
When the number of threads ranges from 25 to 75, the decreasing rate of time consumption slows down with the increase of the number of threads; When the number of threads is greater than 75, the time consumption increases slightly with the increase of the number of threads.
To sum up, in a certain range, with the increase of the number of threads, the efficiency of parallel computing is higher. However, after exceeding a certain range, due to the call of MPI_Send function and MPI_Recv function, the time cost of communication increases greatly, resulting in the overall time-consuming
Increase.
6. Summary
The proposal put forward in this report is to adopt and implement the zoning scheme based on round robin segmentation
Parallelization of set algorithm and Julia set algorithm. The parallelization based on partition scheme is based on the elimination in C programming
Message passing interface (MPI) library. The experimental results show that
The program of the partition scheme based on round robin segmentation proposed by MPI in C programming is significantly accelerated. Therefore, the successful parallelization of the program is proved
7. Appendix
7.1 display of other results
Other image displays generated by Mandelbrot

Other pictures generated by Julia Set:
7.2 source code appendix
7.2.1 mandelbrot source code
#include "mandelbrot.h"
int main(int argc, char **argv)
{
int proc_count, proc_id, retval;
mo_opts_t *opts;
/* MPI initialization*/
if (MPI_Init(&argc, &argv) != MPI_SUCCESS) {
eprintf("MPI initialization failed.\n");
exit(EXIT_FAILURE);
}
/* Get the number of processes available */
MPI_Comm_size(MPI_COMM_WORLD, &proc_count);
if (proc_count < 2) { //The number of processes must be at least 2
eprintf("Number of processes must be at least 2.\n");
finalize_exit(EXIT_FAILURE);
}
/* Get the ID of the current process */
MPI_Comm_rank(MPI_COMM_WORLD, &proc_id);
opts = (mo_opts_t *) malloc(sizeof(*opts));// Open up memory space
if (opts == NULL) {
eprintf("unable to allocate memory for config.\n");
finalize_exit(EXIT_FAILURE);
}
retval = parse_args(argc, argv, opts, proc_id, proc_count); // Configuration information of parameters
if (retval == EXIT_SUCCESS) {
if (proc_id == 0) {
retval = master_proc(proc_count - 1, opts); //id=0 is the root process
} else {
retval = slave_proc(proc_id, opts); //Others are from the process
}
}
free(opts);
MPI_Finalize(); // end
return retval;
}
/*
* Configuration information of parameters
*/
static int parse_args(int argc, char **argv, mo_opts_t *opts, int proc_id, int proc_count)
{
/* Set defaults */
opts->max_iterations = MO_MAXITER; //Maximum number of iterations
opts->width = MO_SIZE; // Width of picture
opts->height = MO_SIZE; // Height of picture
opts->filename = MO_FILENAME; //Stored file name
opts->min_color = MO_COLORMIN; //Lower limit of color
opts->max_color = MO_COLORMAX; //Upper limit of color
opts->color_mask = MO_COLORMASK; //Mask color
opts->blocksize = MO_BLOCKSIZE; //Size of partition
opts->show_progress = MO_PROGRESS; //Display process information
double x_offset = 0;
double y_offset = 0;
double axis_length = MO_N;
const char *opt_string = "c:r:n:hb:p:q:m:x:y:a:o:s";
int optval_int, c, index;
long optval_long;
double optval_double;
opterr = 0;
/* start parsing args */
while ((c = getopt(argc, argv, opt_string)) != -1) {
switch (c) {
case 'b': /* blocksize */
case 'c': /* width */
case 'r': /* height */
case 'n': /* iterations */
optval_int = atoi(optarg);
if (optval_int <= 0) {
if (proc_id == 0) {
print_usage(argv);
eprintf("argument of '-%c' has to be greater than zero.\n", c);
}
return EXIT_FAILURE;
}
if (c == 'c') opts->width = optval_int; else
if (c == 'r') opts->height = optval_int; else
if (c == 'n') opts->max_iterations = optval_int; else
if (c == 'b') opts->blocksize = optval_int;
break;
case 'p': /* colormin */
case 'q': /* colormax */
case 'm': /* colormask */
optval_long = strtol(optarg, NULL, 16);
if (c == 'p') opts->min_color = optval_long; else
if (c == 'q') opts->max_color = optval_long; else
if (c == 'm') opts->color_mask = optval_long;
break;
case 'x': /* xoffset */
case 'y': /* yoffset */
case 'a': /* axis-length */
optval_double = atof(optarg);
if (c == 'x') x_offset = optval_double; else
if (c == 'y') y_offset = optval_double; else
if (c == 'a') {
if (optval_double == 0) {
if (proc_id == 0) {
print_usage(argv);
eprintf("argument of '-%c' cannot be zero.\n", c);
}
return EXIT_FAILURE;
}
axis_length = optval_double;
}
break;
case 'o': /* output */
opts->filename = optarg;
break;
case 's': /* progress */
opts->show_progress = 1;
break;
case 'h': /* help */
if (proc_id == 0) {
print_usage(argv);
}
free(opts);
finalize_exit(EXIT_SUCCESS);
break;
case '?': /* unknown opt */
if (proc_id == 0) {
/* hacky fix: get correct index if length of invalid option is > 2 */
index = (strncmp(argv[0], argv[optind - 1], sizeof(argv)) == 0)
? optind
: optind-1;
print_usage(argv);
eprintf("invalid option '%s'.\n", argv[index]);
}
return EXIT_FAILURE;
break;
default:
break;
}
}
/* blocksize The size of should be divisible by height */
if (opts->height % opts->blocksize != 0) {
if (proc_id == 0) {
print_usage(argv);
eprintf("argument of '-b' has to be a divisor of %d.\n", opts->height);
}
return EXIT_FAILURE;
}
/* Avoid excessive blocksize */
if (opts->blocksize > opts->height/(proc_count - 1)) {
if (proc_id == 0) {
print_usage(argv);
eprintf("argument of '-b' has to be smaller than %d.\n", opts->height/(proc_count-1));
}
return EXIT_FAILURE;
}
/* Calculate the range of the picture */
opts->min_re = x_offset - axis_length;
opts->max_re = x_offset + axis_length;
opts->min_im = y_offset - axis_length;
opts->max_im = y_offset + axis_length;
/* Display configuration information */
if (proc_id == 0) {
if (argc < 2) {
printf("Note: Program invoked with default options.\n" \
" Run '%s -h' for detailed information on available arguments.\n\n", argv[0]);
}
print_params(opts, x_offset, y_offset, axis_length);
}
return EXIT_SUCCESS;
}
/*
* Display configuration information before calculation
*/
static void print_params(mo_opts_t *opts, double x_off, double y_off, double axis_length)
{
printf("Computation parameters:\n" \
" output file %s\n" \
" maximum iterations %d\n" \
" blocksize %d\n" \
" image width %d\n" \
" image height %d\n" \
" minimum color 0x%06lx\n" \
" maximum color 0x%06lx\n" \
" color mask 0x%06lx\n" \
" x-offset %g\n" \
" y-offset %g\n" \
" axis length %g\n" \
" coordinate system range [%g, %g]\n\n",
opts->filename, opts->max_iterations, opts->blocksize, opts->width, opts->height,
opts->min_color, opts->max_color, opts->color_mask, x_off, y_off, axis_length,
opts->min_re, opts->max_re);
}
/*
* Display instructions
*/
static void print_usage(char **argv)
{
printf("\nDynamic MPI mandelbrot algorithm\n\n" \
"usage: %s [options]\n\n" \
"OPTIONS:\n" \
" -h Shows this help.\n" \
" -c {width} Width of resulting image. Has to be positive integer.\n" \
" (default: %d)\n" \
" -r {height} Height of resulting image. Has to be positive integer.\n" \
" (default: %d)\n" \
" -n {iterations} Maximum number of iterations for each pixel. Has to be\n" \
" positive integer (default: %d)\n" \
" -o {filename} Filename of resulting bitmap. (default: %s)\n" \
" -b {blocksize} Number of rows to be assigned to a slave at once.\n" \
" Has to be smaller than (height/slave-count).\n" \
" Has to be a divisor of height. (default: %d)\n" \
" -x {offset} X-offset from [0,0]. (default: %g)\n" \
" -y {offset} Y-offset from [0,0]. (default: %g)\n" \
" -a {length} Absolute value range of x/y-axis, e.g. if length was 2, \n" \
" displayed x/y-values would range from -1 to 1. \n" \
" If the x/y-offsets are set, axis shifts by those offsets.\n" \
" Negative value inverts axis.\n" \
" Has to be non-zero double value. (default: %g)\n" \
" -p {hexnum} Minimum color of the resulting image. (default: 0x%06lx)\n" \
" -q {hexnum} Maximum color of the resulting image. (default: 0x%06lx)\n" \
" -m {hexnum} Hex mask to manipulate color ranges. (default: 0x%06lx)\n" \
" -s Print progress of the computation.\n\n",
argv[0], MO_SIZE, MO_SIZE, MO_MAXITER, MO_FILENAME, MO_BLOCKSIZE, 0.0f, 0.0f,
(double) MO_N, (long) MO_COLORMIN, (long) MO_COLORMAX, (long) MO_COLORMASK);
}
/*
* Running logic of main process
*/
static int master_proc(int slave_count, mo_opts_t *opts)
{
int *rows = (int *) malloc(opts->blocksize*sizeof(*rows));
long *data = (long *) malloc((opts->width + 1)*opts->blocksize*sizeof(*data));
char *rgb = (char *) malloc(3*opts->width*opts->height*sizeof(*rgb));
if (rows == NULL || data == NULL || rgb == NULL) {
eprintf("unable to allocate memory for buffers.\n");
free(rows); free(data); free(rgb);
return EXIT_FAILURE;
}
int proc_id, offset;
double start_time, end_time;
long pixel_color, pixel_pos;
int current_row = 0;
int running_tasks = 0;
int retval = EXIT_SUCCESS;
MPI_Status status;
printf("Computation started.\n");
/* Record start time */
start_time = MPI_Wtime();
/* Initialize row(s) for each slave process */
for (int p = 0; p < slave_count; ++p) {
for (int i = 0; i < opts->blocksize; ++i) {
rows[i] = current_row++;
}
MPI_Send(rows, opts->blocksize, MPI_INT, p + 1, MO_CALC, MPI_COMM_WORLD);
++running_tasks;
}
/* reveice results from slaves until all rows are processed */
while (running_tasks > 0) {
MPI_Recv(data, (opts->width + 1)*opts->blocksize, MPI_LONG, MPI_ANY_SOURCE,
MO_DATA, MPI_COMM_WORLD, &status);
--running_tasks;
proc_id = status.MPI_SOURCE;
/* if there are still rows to be processed, send slave to work again
* otherwise send him to sleep */
if (current_row < opts->height) {
for (int i = 0; i < opts->blocksize; ++i) {
rows[i] = current_row++;
}
MPI_Send(rows, opts->blocksize, MPI_INT, proc_id, MO_CALC, MPI_COMM_WORLD);
++running_tasks;
} else {
MPI_Send(NULL, 0, MPI_INT, proc_id, MO_STOP, MPI_COMM_WORLD);
}
/* store received row(s) in rgb buffer */
for (int i = 0; i < opts->blocksize; ++i) {
offset = opts->width*i;
for (int col = 0; col < opts->width; ++col) {
pixel_color = data[offset + col + 1] & opts->color_mask;
pixel_pos = 3*(opts->width*data[offset] + col);
rgb[pixel_pos] = (char) ((pixel_color >> 16) & 0xFF);
rgb[pixel_pos + 1] = (char) ((pixel_color >> 8) & 0xFF);
rgb[pixel_pos + 2] = (char) (pixel_color & 0xFF);
}
}
/* When the configuration information is required, the progress bar is displayed */
if (opts->show_progress) {
static int rows_processed = 0;
print_progress(rows_processed += opts->blocksize, opts->height);
}
}
/* Get end time */
end_time = MPI_Wtime();
/* Clear progress bar */
if (opts->show_progress) printf("\033[K");
printf("Finished. Computation finished in %g sec.\n\n", end_time - start_time); // Display time
/* Write rgb information to the picture */
printf("Creating bitmap image.\n");
retval = write_bitmap(opts->filename, opts->width, opts->height, rgb);
if (retval == EXIT_SUCCESS) {
printf("Finished. Image stored in '%s'.\n", opts->filename);
} else {
eprintf("failed to write bitmap to file.\n");
}
// Free up memory space
free(rows);
free(data);
free(rgb);
return retval;
}
/*
* Run logic from process
*/
static int slave_proc(int proc_id, mo_opts_t *opts)
{
int *rows = (int *) malloc(opts->blocksize*sizeof(*rows));
long *data = (long *) malloc((opts->width + 1)*opts->blocksize*sizeof(*data));
mo_scale_t *scale = (mo_scale_t *) malloc(sizeof(*scale));
if (rows == NULL || data == NULL || scale == NULL) {
free(rows); free(data); free(scale);
return EXIT_FAILURE;
}
long pixel_color;
int offset;
MPI_Status status;
/* Calculate color scaling factor */
scale->color = (double) (opts->max_color - opts->min_color) /
(double) (opts->max_iterations - 1);
/* Calculate the scaling factor for the image size of the area */
scale->re = (double) (opts->max_re - opts->min_re) / (double) opts->width;
scale->im = (double) (opts->max_im - opts->min_im) / (double) opts->height;
/* If the status is MO_CALC, receive the line and start the calculation */
while ((MPI_Recv(rows, opts->blocksize, MPI_INT, 0, MPI_ANY_TAG, MPI_COMM_WORLD,
&status) == MPI_SUCCESS) && status.MPI_TAG == MO_CALC) {
for (int i = 0; i < opts->blocksize; ++i) {
offset = opts->width*i;
data[offset] = rows[i];
/* Calculate pixel color using mandelbrot algorithm */
for (int col = 0; col < opts->width; ++col) {
pixel_color = mandelbrot(col, rows[i], scale, opts);
data[offset + col + 1] = pixel_color;
}
}
/* Send row(s) to main process */
MPI_Send(data, (opts->width + 1)*opts->blocksize, MPI_LONG, 0, MO_DATA, MPI_COMM_WORLD);
}
//Free up memory space
free(rows);
free(data);
free(scale);
return EXIT_SUCCESS;
}
/*
* Calculate pixel color using mandelbrot algorithm
*/
static long mandelbrot(int col, int row, mo_scale_t *scale, mo_opts_t *opts)
{
mo_complex_t a, b;
a.re = a.im = 0;
/* Zoom the display coordinates to the actual area */
b.re = opts->min_re + ((double) col*scale->re);
b.im = opts->min_im + ((double) (opts->height - 1 - row)*scale->im);
/* Calculate z0, z1 until divergence or maximum iteration */
int n = 0;
double r2, tmp;
do {
tmp = a.re*a.re - a.im*a.im + b.re;
a.im = 2*a.re*a.im + b.im;
a.re = tmp;
r2 = a.re*a.re + a.im*a.im;
++n;
} while (r2 < MO_THRESHOLD && n < opts->max_iterations);
/* Scale the color and return */
return (long) ((n - 1)*scale->color) + opts->min_color;
}
/*
* Draw progress bar
*/
static inline void print_progress(int rows_processed, int row_count)
{
int r = row_count/MO_PUPDATE;
/* Update Mo only_ Pupdate times */
if (r == 0 || rows_processed % r != 0) return;
/* Calculate ratio and current position */
float ratio = rows_processed/(float) row_count;
int pos = ratio*MO_PWIDTH;
/* Draw progress bar */
printf("%3d%% [", (int) (ratio*100));
for (int i = 0; i < pos; ++i) printf("=");
for (int i = pos; i < MO_PWIDTH; ++i) printf(" ");
/* Press enter to overwrite the next progress bar update */
printf("]\r");
}
/*
* Draw picture
*/
static int write_bitmap(const char *filename, int width, int height, char *rgb)
{
int i, j, pixel_pos;
int bytes_per_line;
unsigned char *line;
FILE *file;
mo_bmp_header_t bmph;
/* The length of each line must be a multiple of 4 bytes */
bytes_per_line = (3*(width + 1)/4)*4;
bmph.type[0] = 'B';
bmph.type[1] = 'M';
bmph.offbits = 54;
bmph.fsize = bmph.offbits + bytes_per_line*height;
bmph.reserved = 0;
bmph.hsize = 40;
bmph.width = width;
bmph.height = height;
bmph.planes = 1;
bmph.bit_count = 24;
bmph.compression = 0;
bmph.size_image = bytes_per_line*height;
bmph.x_pels_per_meter = 0;
bmph.y_pels_per_meter = 0;
bmph.clr_used = 0;
bmph.clr_important = 0;
file = fopen(filename, "wb");
if (file == NULL) {
eprintf("unable to open file '%s'.\n", filename);
return EXIT_FAILURE;
}
/* write header */
fwrite(&bmph.type, 2, 1, file);
fwrite(&bmph.fsize, 4, 1, file);
fwrite(&bmph.reserved, 4, 1, file);
fwrite(&bmph.offbits, 4, 1, file);
fwrite(&bmph.hsize, 4, 1, file);
fwrite(&bmph.width, 4, 1, file);
fwrite(&bmph.height, 4, 1, file);
fwrite(&bmph.planes, 2, 1, file);
fwrite(&bmph.bit_count, 2, 1, file);
fwrite(&bmph.compression, 4, 1, file);
fwrite(&bmph.size_image, 4, 1, file);
fwrite(&bmph.x_pels_per_meter, 4, 1, file);
fwrite(&bmph.y_pels_per_meter, 4, 1, file);
fwrite(&bmph.clr_used, 4, 1, file);
fwrite(&bmph.clr_important, 4, 1, file);
line = (unsigned char *) malloc(bytes_per_line*sizeof(*line));
if (line == NULL) {
eprintf("unable to allocate memory for line buffer.\n");
fclose(file);
return EXIT_FAILURE;
}
/* Write rgb information */
for (i = height - 1; i >= 0; i--) {
for (j = 0; j < width; j++) {
pixel_pos = 3*(width*i + j);
line[3*j] = rgb[pixel_pos + 2];
line[3*j + 1] = rgb[pixel_pos + 1];
line[3*j + 2] = rgb[pixel_pos];
}
fwrite(line, bytes_per_line, 1, file);
}
free(line);
fclose(file);
return EXIT_SUCCESS;
}
7.2.2 Julia source code
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include "mpi.h"
#include "cmplx.h"
#define FULL_WIDTH 1024
#define CHUNK_WIDTH 32
#define MAX_ITER 1000
void plot(int* image_arr, FILE* img);
long iterator(Complex c, double im, double re);
int main(int argc, char* argv[])
{
int *image_arr;
int pixel_YX[3];
int Y_start, X_start, CUR_CHUNK, disp = 0;
int i, j;
Complex c;
FILE *img;
int NUM_CHUNKS = (FULL_WIDTH / CHUNK_WIDTH) * (FULL_WIDTH / CHUNK_WIDTH);
/** Time correlation**/
double start, stop;
float elapsed_time;
/** MPI Related variables**/
MPI_Status status, stat_recv;
MPI_Request request;
MPI_Datatype CHUNKxCHUNK, CHUNKxCHUNK_RE;
int rankID, numProcs, numSlaves;
/** MPI Initialization of environment**/
MPI_Init(&argc, &argv);
MPI_Barrier(MPI_COMM_WORLD);
MPI_Comm_size(MPI_COMM_WORLD, &numProcs);
MPI_Comm_rank(MPI_COMM_WORLD, &rankID);
MPI_Barrier(MPI_COMM_WORLD);
/** Create type**/
int full_sizes[2] = {FULL_WIDTH, FULL_WIDTH};
int sub_sizes[2] = {CHUNK_WIDTH, CHUNK_WIDTH};
int starting[2] = {0, 0};
int sendcounts[numProcs];
int displs[numProcs];
/** Create CHUNK */
MPI_Type_create_subarray(
2,
full_sizes,
sub_sizes,
starting,
MPI_ORDER_C,
MPI_INT,
&CHUNKxCHUNK
);
/** Set offset**/
MPI_Type_create_resized(
CHUNKxCHUNK,
0,
CHUNK_WIDTH * sizeof(int),
&CHUNKxCHUNK_RE
);
/** Submit the type to use**/
MPI_Type_commit(&CHUNKxCHUNK_RE);
/** Number of slave processes */
numSlaves = numProcs - 1;
/** Print basic information */
if(rankID == 0)
printf("Runtime Stats:\n\tNum Procs:\t%d\n\tNum Slaves:\t%d\n", numProcs, numSlaves);
MPI_Barrier(MPI_COMM_WORLD);
/** Value of parameter C */
c.re = -0.4;
c.im = 0.5;
/** Main process */
if(rankID == 0) {
img = fopen("t6.ppm", "w");
if(img == NULL) {
printf("Could not open handle to image\n");
return 1;
}
fprintf(img, "P6\n%d %d 255\n", FULL_WIDTH, FULL_WIDTH);
image_arr = (int *)malloc(FULL_WIDTH * FULL_WIDTH * sizeof(int));
/** Start timer */
start = MPI_Wtime();
/** X and Y are calculated and distributed to each node**/
for(pixel_YX[2] = 0; pixel_YX[2] < numSlaves; pixel_YX[2]++) {
pixel_YX[0] = (pixel_YX[2] / (FULL_WIDTH / CHUNK_WIDTH)) * CHUNK_WIDTH; // Y
pixel_YX[1] = (pixel_YX[2] % (FULL_WIDTH / CHUNK_WIDTH)) * CHUNK_WIDTH; // X
MPI_Send(
pixel_YX,
3,
MPI_INT,
pixel_YX[2] + 1,
0,
MPI_COMM_WORLD
);
}
/** Update current chunk and pixel */
pixel_YX[2] = numSlaves;
pixel_YX[0] = (pixel_YX[2] / (FULL_WIDTH / CHUNK_WIDTH)) * CHUNK_WIDTH; // Y
pixel_YX[1] = (pixel_YX[2] % (FULL_WIDTH / CHUNK_WIDTH)) * CHUNK_WIDTH; // X
/** Receives the current block from X and sends the next block to X */
while(pixel_YX[2] < NUM_CHUNKS) {
/** Detect the receiving buffer, calculate the displacement in the array, and receive */
MPI_Probe(MPI_ANY_SOURCE, MPI_ANY_TAG, MPI_COMM_WORLD, &stat_recv);
disp = ((stat_recv.MPI_TAG * CHUNK_WIDTH) % FULL_WIDTH) +
(((stat_recv.MPI_TAG * CHUNK_WIDTH) / FULL_WIDTH) * CHUNK_WIDTH * FULL_WIDTH);
MPI_Recv(
image_arr + disp,
1,
CHUNKxCHUNK_RE,
stat_recv.MPI_SOURCE,
stat_recv.MPI_TAG,
MPI_COMM_WORLD,
&status
);
#ifdef DEBUG
printf("Proc: MA\tJob: Recieved [# %d]\n", stat_recv.MPI_TAG);
#endif
MPI_Send(
pixel_YX,
3,
MPI_INT,
status.MPI_SOURCE,
0,
MPI_COMM_WORLD
);
/** pixel_YX To next block value */
pixel_YX[2]++;
pixel_YX[0] = (pixel_YX[2] / (FULL_WIDTH / CHUNK_WIDTH)) * CHUNK_WIDTH;
pixel_YX[1] = (pixel_YX[2] % (FULL_WIDTH / CHUNK_WIDTH)) * CHUNK_WIDTH;
}
/** Final reception matches initial transmission */
for(i = 0; i < numSlaves; i++) {
MPI_Probe(MPI_ANY_SOURCE, MPI_ANY_TAG, MPI_COMM_WORLD, &stat_recv);
disp = ((stat_recv.MPI_TAG * CHUNK_WIDTH) % FULL_WIDTH) + (((stat_recv.MPI_TAG * CHUNK_WIDTH) / FULL_WIDTH) * CHUNK_WIDTH * FULL_WIDTH);
MPI_Recv(
image_arr + disp,
1,
CHUNKxCHUNK_RE,
stat_recv.MPI_SOURCE,
stat_recv.MPI_TAG,
MPI_COMM_WORLD,
&status
);
#ifdef DEBUG
printf("Proc: MA\tJob: Recieved [# %d]\n", stat_recv.MPI_TAG);
#endif
}
/** End current process**/
for(i = 0; i < numSlaves; i++)
MPI_Send(
0,
0,
MPI_INT,
i + 1,
0xFFFF,
MPI_COMM_WORLD
);
/** Stop the timer and calculate elapsed_time */
stop = MPI_Wtime();
elapsed_time = stop - start;
#ifdef DEBUG
printf("Proc: Ma\tJob: Plotting image\n");
#endif
plot(image_arr, img);
printf("Algorithm completed for,\n\t%d * %d pixels\n\t%d maximum iterations\n\t\tin %f seconds.\n", \
FULL_WIDTH, FULL_WIDTH, \
MAX_ITER, \
elapsed_time);
fclose(img);
}
else {
/** Everyone assigns their image_arr part */
image_arr = (int *)malloc(CHUNK_WIDTH * CHUNK_WIDTH * sizeof(int));
/** Infinite loop until 'break;' */
while(1) {
MPI_Recv(
pixel_YX,
3,
MPI_INT,
0,
MPI_ANY_TAG,
MPI_COMM_WORLD,
&status
);
/** Check whether the call is terminated */
if(status.MPI_TAG == 0xFFFF) {
printf("Proc: %d \tJob: Exiting\n", rankID);
break;
}
CUR_CHUNK = pixel_YX[2];
#ifdef DEBUG
printf("Proc: %d \tChunk %d \tJob: Algorithm\n", rankID, CUR_CHUNK);
#endif
/** For each Y value */
for(i = 0; i < CHUNK_WIDTH; i++) {
for(j = 0; j < CHUNK_WIDTH; j++) {
image_arr[(i * CHUNK_WIDTH) + j] = iterator(
c,
-(((pixel_YX[0] + i) - (FULL_WIDTH / 2)) / (double) FULL_WIDTH) * 2,
(((pixel_YX[1] + j) - (FULL_WIDTH / 2)) / (double) FULL_WIDTH) * 2
);
}
}
#ifdef DEBUG
printf("Proc: %d \tJob: Returning [# %d]\n", rankID, CUR_CHUNK);
#endif
/** Send part calculation imaging to MASTER */
MPI_Send(
image_arr,
CHUNK_WIDTH * CHUNK_WIDTH,
MPI_INT,
0,
CUR_CHUNK,
MPI_COMM_WORLD
);
}
}
free(image_arr);
/** End the running environment of MPI */
MPI_Type_free(&CHUNKxCHUNK_RE);
MPI_Finalize();
fflush(stdout);
return 0;
}
/**
Main iterative function of program
*/
long iterator(Complex c, double im, double re)
{
Complex z;
long itCount = 0;
z.re = re;
z.im = im;
for(; itCount < MAX_ITER; itCount++) {
z = cmplx_add(cmplx_squared(z), c);
if(cmplx_magnitude(z) > 4)
break;
}
return itCount + 1;
}
/**
Drawing graphics
*/
void plot(int* image_arr, FILE* img)
{
int i, j;
unsigned char line[3 * FULL_WIDTH];
for(i = 0; i < FULL_WIDTH; i++) {
for(j = 0; j < FULL_WIDTH; j++) {
if (*(image_arr + j + (i * FULL_WIDTH)) <= 63) {
line[3 * j] = 255;
line[3 * j + 1] = line[3 * j + 2] =
255 - 4 * *(image_arr + j + (i * FULL_WIDTH));
} else {
line[3 * j] = 255;
line[3 * j + 1] = *(image_arr + j + (i * FULL_WIDTH)) - 63;
line[3 * j + 2] = 0;
}
if (*(image_arr + j + (i * FULL_WIDTH)) == 320)
line[3 * j] = line[3 * j + 1] = line[3 * j + 2] = 255;
}
fwrite(line, 1, 3 * FULL_WIDTH, img);
}
}
7.3 references
https://github.com/BodneyC/JuliaSet