1, Overview
HashMap
The general structure of the hash table is shown in the figure below. The hash table is an array. We often call each node in the array a bucket, and each node in the hash table is used to store a key value pair. When inserting elements, if there is a conflict (that is, multiple key value pairs are mapped to the same bucket), the conflict will be solved in the form of linked list. Because there may be multiple key value pairs on a bucket, when searching, first locate the bucket through the hash value of the key, and then traverse all key value pairs on the bucket to find the key
Equal key value pairs to obtain value
.
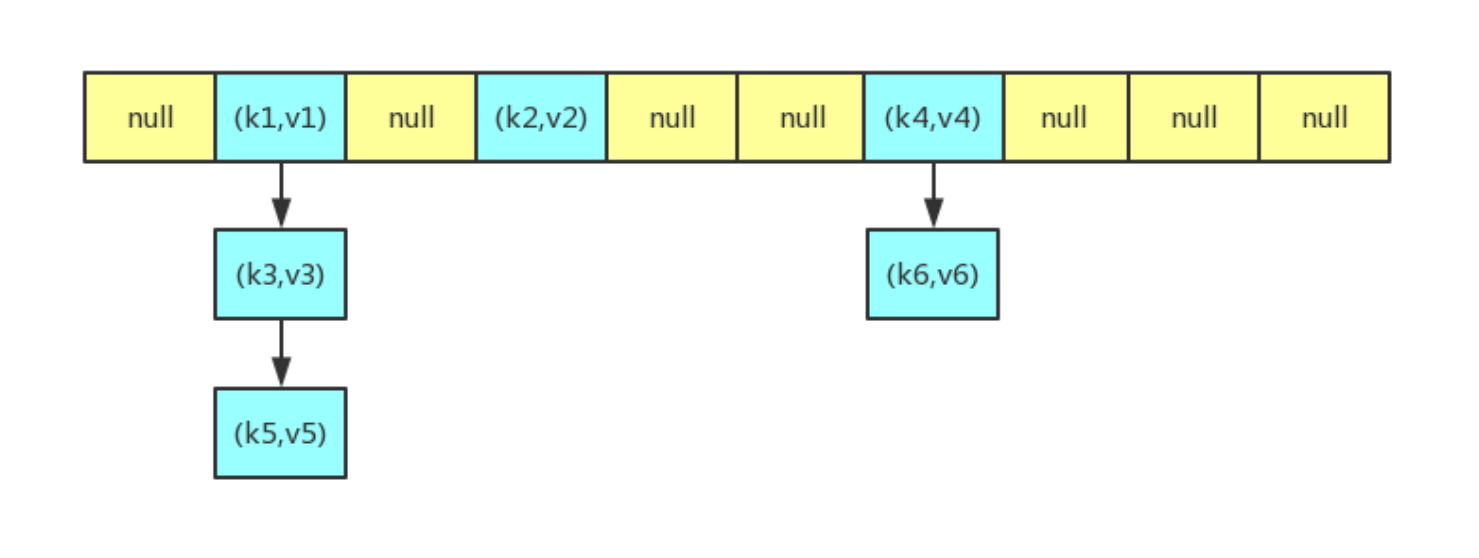
2, Attributes
HashMap
Class contains some important properties
influence
HashMap
Two important parameters of performance:
"initial capacity"
(initialization capacity) and
”Simply put, the capacity is the number of hash table buckets, and the load factor is the ratio of the number of key value pairs to the length of the hash table. When the ratio exceeds the load factor, HashMap
Will proceed
rehash operation for capacity expansion.
//The default initial capacity is 16 static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; //The maximum capacity is 2 ^ 30 static final int MAXIMUM_CAPACITY = 1 << 30; //The default load factor is 0.75 static final float DEFAULT_LOAD_FACTOR = 0.75f; //The critical value of becoming a tree structure is 8 static final int TREEIFY_THRESHOLD = 8; //The critical value of restoring chain structure is 6 static final int UNTREEIFY_THRESHOLD = 6; //Hashtable transient Node<K,V>[] table; //The number of key value pairs in the hash table transient int size; //The number of times the hash table was modified transient int modCount; //It is calculated through the capacity*load factor. When the size reaches this value, the capacity expansion operation will be carried out int threshold; //Load factor final float loadFactor; //When the size of the hash table exceeds this threshold, the chain structure will be transformed into a tree structure. Otherwise, only capacity expansion will be taken to try to reduce conflicts static final int MIN_TREEIFY_CAPACITY = 64;
Here is
Node
Class, which is
HashMap
A static internal class in the hash table. Each Node in the hash table is a Node
Type. As we can see,
Node
Class has
4
Attributes, except
key
And value, and
hash
and
next
Two properties.
hash
Is used to store
key
The hash value of,
next is used to point to subsequent nodes when building a linked list.
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) && Objects.equals(value, e.getValue()))
return true;
}
return false;
}3, Method
1. get method
//The get method mainly calls the getNode method, so the focus is on the implementation of the getNode method
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
//If the hash table is not empty & & the bucket corresponding to the key is not empty
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
//Direct hit
if (first.hash == hash && // always check first n
ode
((k = first.key) == key || (key != null && ke
y.equals(k))))
return first;
//Determine whether there are subsequent nodes
if ((e = first.next) != null) {
//If the current bucket uses the red black tree to handle the conflict, call the get method of the red black tree to get the node
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
//If it is not a red black tree, it is a traditional chain structure. Judge whether the key exists in the chain by means of circulation
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null &&
key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
The implementation steps are as follows:
1
, passed
hash
Get the value
key
Bucket mapped to.
2
. on bucket
key
That's what you're looking for
key
, then hit directly.
3
. on bucket
key
Not to find
key
, view subsequent nodes:
(
1
)If the subsequent node is a tree node, find the node by calling the tree method
key
.
(
2
)If the subsequent node is a chain node, find the node by looping through the chain
key
.
2. put method
//The specific implementation of the put method is also in the putVal method, so we focus on the putVal method below
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIf
Absent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
//If the hash table is empty, create a hash table first
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
//If the current bucket has no collision, insert the key value pair directly and finish
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
//If the key of the node on the bucket is the same as the current key, you are the node i am looking for
if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
e = p;
//If the conflict is handled by the red black tree, insert the key value pair through the putTreeVal method of the red black tree
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
//Otherwise, it is the traditional chain structure
else {
//Loop traversal is used to judge whether there are duplicate key s in the chain
for (int binCount = 0; ; ++binCount) {
//If no duplicate key is found at the end of the chain, it means that the HashMap does not contain the key
if ((e = p.next) == null) {
//Create a new node and insert it into the tail
p.next = newNode(hash, key, value, null);
//If the length of the chain is greater than tree_ The threshold value of threshold changes the chain into a red black tree
if (binCount >= TREEIFY_THRESHOLD - 1)
// -1 for 1st
treeifyBin(tab, hash);
break;
}
//Duplicate key found
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
//This indicates that a duplicate key was found in the above operation, so the value of the key is replaced with a new value
if (e != null) { // existing mapping for key V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
//Determine whether capacity expansion is required
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
The implementation steps are as follows:
1
First pass
hash
Value calculated
key
To which bucket.
2
. if there is no collision on the bucket, insert it directly.
3
. if a collision occurs, you need to deal with the conflict:
(
1
)If the bucket uses a red black tree to handle conflicts, the method of the red black tree is called to insert.
(
2
)Otherwise, the traditional chain method is used to insert. If the length of the chain reaches the critical value, the chain is transformed into a red black tree.
4
. if there is a duplicate key in the bucket, replace the key with a new value.
5
If
size
If it is greater than the threshold, the capacity will be expanded.
3. remove method
//The specific implementation of the remove method is in the removeNode method, so we focus on the following removeNode method
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ? null : e.value;
}
final Node<K,V> removeNode(int hash, Object key, Object value, boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
//If the bucket mapped to the current key is not empty
if ((tab = table) != null && (n = tab.length) > 0 && (p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
//If the node on the bucket is the key to be found, it will be hit directly
if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
node = p;
else if ((e = p.next) != null) {
//If the conflict is handled as a red black tree, a tree node is built
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
//If the conflict is handled in a chained manner, the node is found by traversing the linked list
else {
do {
if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
//Check whether the value of the found key matches the key to be deleted
if (node != null && (!matchValue || (v = node.value) == value || (value != null &&
value.equals(v)))) {
//Delete the node by calling the method of red black tree
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
//Use the operation of linked list to delete nodes
else if (node == p)
tab[index] = node.next;
else
p.next = node.next;
++modCount;
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}4. hash method
stay
get
Methods and
put
All methods need to be calculated first
key
The main calculation codes are as follows:
(n - 1) & hash
In the code above
n
Refers to the size of the hash table,
hash
refer to
key
Hash value of,
hash
It is calculated by the following method, using the method of secondary hash, where key
of
hashCode
Method is a native method:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
this
hash
Method first pass
key
of
hashCode
Method to obtain a hash value, and then compare the hash value with its high 16
Do an XOR operation on the hash value of bit to get the final hash value. The calculation process can refer to the following figure. Why do you want to do this? The note explains this: if when n
Very small, assuming
64
If so, then
n-1 is 63
(
0x111111
), such a value is similar to
hashCode()
In fact, only the last 6 bits of the hash value are used. If the high-order change of the hash value is large and the low-order change is small, it is easy to cause conflict. Therefore, the high-order and low-order are used here to solve this problem.

It is precisely because of this operation with that determines
HashMap
The size of can only be
2
To the power of, think about it, if it's not 2
What happens to the power of? Even if you're creating
HashMap
When the initial size is specified, the HashMap will also call the following method to adjust the size during construction:
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
The function of this method may not seem very intuitive, but its actual function is to
cap
Becomes the first greater than or equal to 2
The number to the power of. For example,
16
still
16
,
13
Will be adjusted to
16
,
17
Will be adjusted to
32
.
5. resize method
HashMap
Used in capacity expansion
rehash
The method is very ingenious, because each expansion is doubled, which is different from the original calculation (n-1
)
&hash
There is only one more result
bit
Bit, so the node is either in its original position or assigned to“
Original position
+
Old capacity
"
This position. For example, the original capacity is 32
, then you should take it
hash
Follow
31
(
0x11111
)Do and operate; The capacity is expanded to 64
After the capacity, you should take it
hash
Follow
63
(
0x111111
)Do and operate. Compared with the original, the new capacity is only
One more
bit
Bit, assuming that the original position is
23
Well, when the new one
bit
The calculation result of bit is
0, the node is still at 23
; On the contrary, the calculation result is
1
When, the node is assigned to
23+31
On the bucket. It is precisely because of such a clever rehash
Way to ensure
rehash
After that, the number of nodes on each bucket must be less than or equal to the number of nodes on the original bucket, that is, rehash is guaranteed
There will be no more serious conflict.
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
//Calculate the size after capacity expansion
if (oldCap > 0) {
//If the current capacity exceeds the maximum capacity, it cannot be expanded
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
//If the maximum value is not exceeded, it will be expanded to twice the original value
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >=
DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies
using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE);
}
//New resize threshold
threshold = newThr;
//Create a new hash table
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
//Traverse each bucket of the old hash table and recalculate the new position of the elements in the bucket
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
//If there is only one key value pair on the bucket, it is inserted directly
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
//If the conflict is handled through the red black tree, call relevant methods to separate the tree
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
//If you use a chain to handle conflicts
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
//Calculate the new position of the node through the above method
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
Here is a place to note that some articles point out that when the hash table
Bucket occupancy
It is wrong to expand capacity when the threshold is exceeded; In fact, when the number of key value pairs in the hash table
Capacity expansion is only carried out when the threshold is exceeded.