In depth array expansion application II

content syllabus

• Bubble sorting
• Select sort
• Insert sort
• Array related interview questions

Bubble sorting

Bubble Sort is a relatively simple sorting algorithm in the field of computer science.

It repeatedly visits the element column to be sorted, compares two adjacent elements in turn, and exchanges them if the order (e.g. from large to small and from Z to A) is wrong. The work of visiting elements is repeated until no adjacent elements need to be exchanged, that is, the element column has been sorted.

The name of this algorithm comes from the fact that the smaller elements will slowly "float" to the top of the sequence (in ascending or descending order) through exchange, just as the bubbles of carbon dioxide in carbonated drinks will eventually float to the top, so it is called "bubble sorting".

The core idea of bubble sorting is as follows:

Compare adjacent elements. If the first one is bigger than the second, exchange them.

Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. At this point, the last element should be the largest number.

Repeat the above steps for all elements except the last one.

Continue to repeat the above steps for fewer and fewer elements at a time until no pair of numbers need to be compared.

The schematic diagram is as follows:

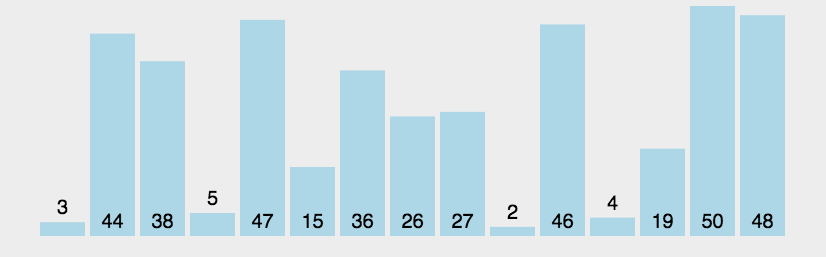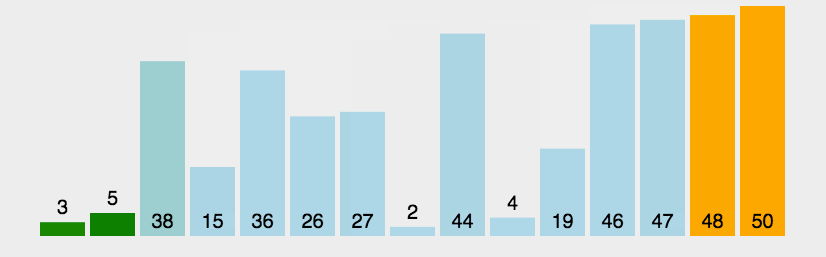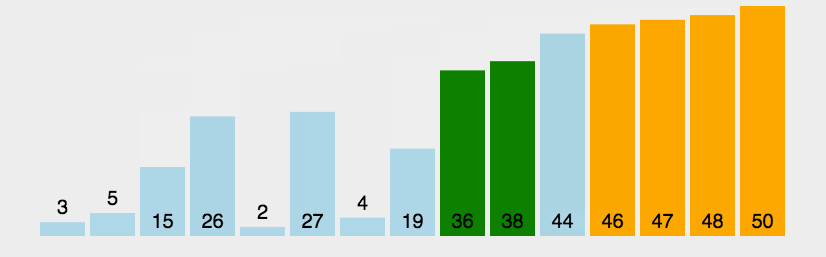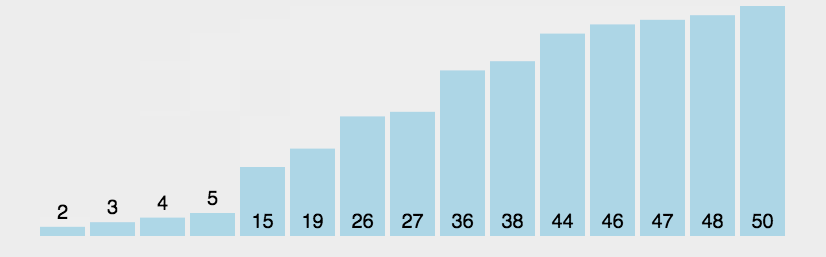
The following is the specific implementation code of bubble sorting:

// Break down and break down big problems into small ones
// Try it. Take a specific number and try it
// So we find a specific array to analyze
// [3, 8, 1, 5]

// First bubbling
// Compare 3 and 8 without exchanging [3, 8, 1, 5]
// Compare 8 with 1 and exchange [3, 1, 8, 5]
// Compare 8 and 5 and exchange [3, 1, 5, 8]

// [3, 1, 5, 8]
// Second bubbling
// Compare 3 with 1 and exchange [1, 3, 5, 8]
// Compare 3 and 5 without exchanging [1, 3, 5, 8]

// [1, 3, 5, 8]
// Third bubbling
// Compare 1 and 3 without exchanging [1, 3, 5, 8]

var arr = [3, 5, 8, 1, 7, -2, 6, 12, -7, 24, 18];

function bubbleSort(arr) {
    var temp = null; // Temporary variable, because we will exchange two numbers later
    // The outer for loop is used to control the number of bubbles
    for (var i = 0; i < arr.length - 1; i++) {
        // The inner for loop is used to control the number of bubble comparisons
        // Because the number of bubble comparisons will be reduced, so -i
        for (var j = 0; j < arr.length - 1 - i; j++) {
            // Bubbling is always compared with two adjacent numbers
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

bubbleSort(arr);
console.log(arr);

Select sort

Selection sort is a simple and intuitive sorting algorithm.

Its working principle is: select the smallest (or largest) element from the data elements to be sorted for the first time, store it at the beginning of the sequence, then find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence. And so on until the number of all data elements to be sorted is zero.

The schematic diagram is as follows:

The following is the specific implementation code of selection sorting:

var arr = [3, 5, 8, 1, 7, -2, 6, 12, -7, 24, 18];

function selectionSort(arr) {
    var min = 0; // The index used to record the minimum value
    var temp = null; // Used to exchange two variables and store temporary values
    // The outer for loop traverses the entire array
    // Because the last number does not need to be compared
    for (var i = 0; i < arr.length - 1; i++) {
        min = i;
        // The inner for loop also traverses the entire array, but it starts from the next item of the current number
        for (var j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[min]) {
                // Update the subscript of the minimum number
                min = j;
            }
        }
        // After the whole for loop runs, min must store the subscript of the minimum value of the array
        // Then we'll exchange at this time
        if (min !== i) {
            temp = arr[min];
            arr[min] = arr[i];
            arr[i] = temp;
        }
    }
}
selectionSort(arr);
console.log(arr);

Homework practice

Consider the following code, What will be printed ？

var arr = [23, 18, 1, 9, 7, 6];
var i = 0;
var pos;
while (i < arr.length - 3) {
    pos = i;
    for (var j = i + 1; j < arr.length; j++) {
        if (arr[j] < arr[pos]) {
            pos = j;
        }
    }
    var temp = arr[pos];
    arr[pos] = arr[i];
    arr[i] = temp;
    i++
}
console.log(arr);

A. {23, 18, 1, 9, 7, 6}
B. {1, 9, 7, 6, 23, 18}
C. {1, 6, 7, 9, 23, 18}
D. {1, 6, 7, 9, 18, 23}
E. {1, 23, 18, 9, 7, 6}

Summary: bubble sorting is to compare two adjacent numbers each time, and the last number in a round of comparison is the largest (or smallest), while selection sorting is to select the smallest (or largest) number by comparing all the numbers behind the current number

Insert sort

The insertion sort starts with index 1 and attempts to insert each subsequent element into the correct position of the ordered part (i.e. the left part of the current position of the outer loop).

The algorithm will empty the position of the value to be inserted by moving the subsequent element to the right by one bit. The move right operation will continue until the correct position is found or the beginning of the array has been reached (proving that the value to be inserted is actually the minimum value of the sorted part).

Generally speaking, insertion sorting is implemented on the array in place. The specific algorithm is described as follows:

1. Starting from the first element, the element can be considered to have been sorted;
2. Take out the next element and scan from back to front in the sorted element sequence;
3. If the element (sorted) is larger than the new element, move the element to the next position;
4. Repeat step 3 until the sorted element is found to be less than or equal to the position of the new element;
5. After inserting the new element into this position;
6. Repeat steps 2 to 5.

The schematic diagram is as follows:

The specific implementation code of insert sorting is as follows:

var arr = [3, 5, 8, 1, 7, -2, 6, 12, -7, 24, 18];
function insertSort(arr) {
    var i, j, insertNode; // Data to insert
    // Starting with the second element of the array, the loop inserts the elements in the array
    for (i = 1; i < arr.length; i++) {
        // Set the second element in the array as the data to be inserted in the first cycle
        insertNode = arr[i];
        j = i - 1;
        // If the element to be inserted is smaller than the j-th element, move the j-th element backward
        while ((j >= 0) && insertNode < arr[j]) {
            arr[j + 1] = arr[j];
            j--;
        }
        // Insert insertNote into the array until the element to be inserted is not less than the j-th element
        arr[j + 1] = insertNode;
    }
}
insertSort(arr);
console.log(arr);

Homework practice

Consider the following code, What will be printed ?

var arr = [13, 18, 11, 29, 1];
var pos;
for (var i = 1; i < arr.length - 2; i++) {
    pos = arr[i];
    var j = i - 1;
    while (j >= 0 && pos < arr[j]) {
        arr[j + 1] = arr[j];
        j--;
    }
    arr[j + 1] = pos;
}
console.log(arr);

A. {13, 18, 11, 29, 1}
B. {13, 18, 29, 29, 1}
C. {1, 11, 13, 18, 29}
D. {11, 13, 18, 29, 1}
E. {1, 11, 13, 29, 18}

Array related interview questions

First question

Given two arrays, the intersection, union, difference and complement of the two arrays are obtained respectively.

For example, given a = [1, 2, 3, 4, 5], b = [2, 4, 6, 8, 10]. The intersection of a and b is [2,4], the complement of a and b: [1,3,5,6,8,10], the union of a and b: [1,2,3,4,5,6,8,10], and the difference of a and b: [1,3,5]

answer:

Before solving this problem, we first need to review the concepts of intersection, union, difference and complement in mathematics.

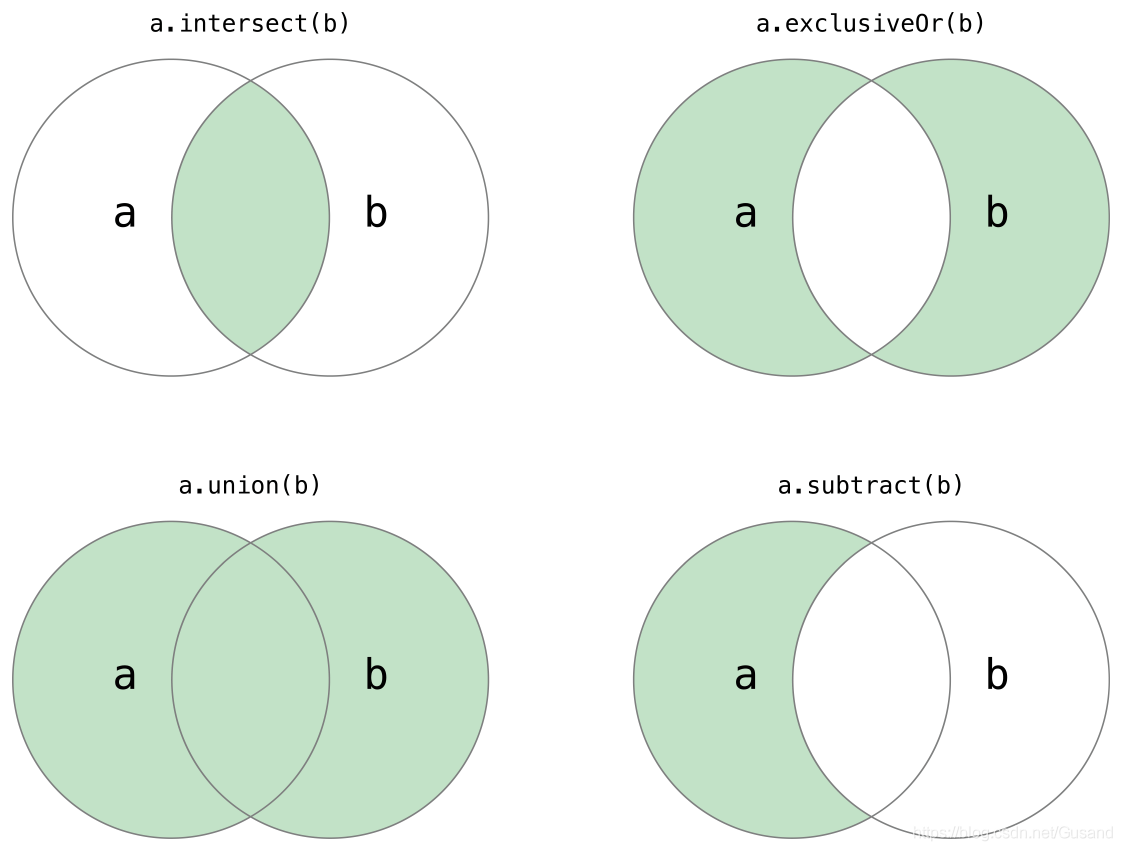
• Intersection: a collection of elements belonging to a or b, that is, a & b (Figure 1)
• Complement: the set of elements of the non intersecting parts of a and b, that is, a ^ b (Fig. 2)
• Union: a set of elements belonging to a or b, that is, a | b (Figure 3)
• Difference set: the set of all elements belonging to a but not to b, that is, a - b (Figure 4)

var a = [1, 2, 3, 4, 5];
var b = [2, 4, 6, 8, 10];

// intersection
// Idea: traverse array A and return the elements in array a that are in array b
var intersect = a.filter(function (item) {
    return b.indexOf(item) !== -1
})

// Complement
// Idea: traverse array a to find those elements in array a that do not exist in array b
// Traverse the b array to find those elements in the b array that do not exist in the a array
// The last two arrays are spliced
var complement = a.filter(function (item) {
    return b.indexOf(item) === -1
}).concat(b.filter(function (item) {
    return a.indexOf(item) === -1
}))

// Union
// Idea: find the elements in array b that do not exist in array a, and then splice them with array a
var unionSet = a.concat(b.filter(function (item) {
    return a.indexOf(item) === -1
}));

// Difference set
// Idea: traverse array A and find the elements in array a that are not in array b
var minus = a.filter(function (item) {
    return b.indexOf(item) === -1
})
console.log("array a:", a);
console.log("array b:", b);
console.log("a And b Intersection of:", intersect);
console.log("a And b Complement of:", complement);
console.log("a And b Union of:", unionSet);
console.log("a And b Difference set of:", minus);

Second question

Combine the two arrays into one array

Please combine two arrays ['A1', 'A2', 'B1', 'C1', 'C2', 'C3', 'D3', 'D2'] and ['a', 'B', 'C','d '] into

[ 'A1', 'A2', 'A', 'B1', 'B', 'C1', 'C2', 'C3', 'C', 'D2', 'D3', 'D' ].

Problem solving idea: since we want to merge into an array, we can do the merging operation first, and then sort according to certain rules.

answer:

var arr1 = ['A1', 'A2', 'B1', 'C1', 'C2', 'C3', 'D3', 'D2'];
var arr2 = ['A', 'B', 'C', 'D'];
console.log(
    arr1.concat(arr2).sort(
        (v2, v1) => (
            v2.codePointAt(0) - v1.codePointAt(0) ||
            v1.length - v2.length ||
            v2.codePointAt(1) - v1.codePointAt(1)
        )
    )
);

After learning ES6 later, the merged array can also be written as follows:

[...arr1, ...arr2]

Question 3

Given an array arr, write a function to move all zeros to the end of the array while maintaining the relative order of non-zero elements.

For example, input [0, 0, 1, 0, 3, 12], and then output [1, 3, 12, 0, 0, 0].

answer:

/**
 * @param {number[]} arr
 * @return {void} Do not return anything, modify arr in-place instead.
 */
var moveZeroes = function (arr) {
    var count = 0;
    // Traverse the entire array
    for (var i = 0; i < arr.length; i++) {
        if (arr[i] === 0) {
            arr.splice(i, 1); // If the current item is 0, it needs to be deleted
            i--; // The next one will become the previous one, so it needs to be judged again
            count++; // Counter technology
        }
    }
    // How many zeros are deleted? Finally, how many zeros need to be filled at the end of the array
    for (var i = 0; i < count; i++) {
        arr.push(0);
    }
};

var arr = [0, 0, 1, 0, 3, 12];
moveZeroes(arr);
console.log(arr); // [ 1, 3, 12, 0, 0 ]

-EOF-