preface
Infix expression is the expression we often use in addition, subtraction, multiplication and division. Suffix expression is a computer-friendly expression. The computer can use two stacks to calculate the input calculation string
Tip: the following is the main content of this article. The following cases can be used for reference
1, Suffix expression
Suffix expression is also called inverse Polish. It is not difficult to realize the inverse Polish algorithm, but why convert the seemingly simple infix expression into complex inverse Polish? The reason is that this simple is relative to the human thinking structure. For computers, the middle order expression is a very complex structure. In contrast, the inverse Polish structure is relatively simple and easy to understand in the view of the computer. Because the memory structure commonly used by computers is a stack structure, it executes the order of first in and last out.
The suffix expression of (a+b)c-(a+b)/e is ab+cab+e/-
2, Infix to suffix mode
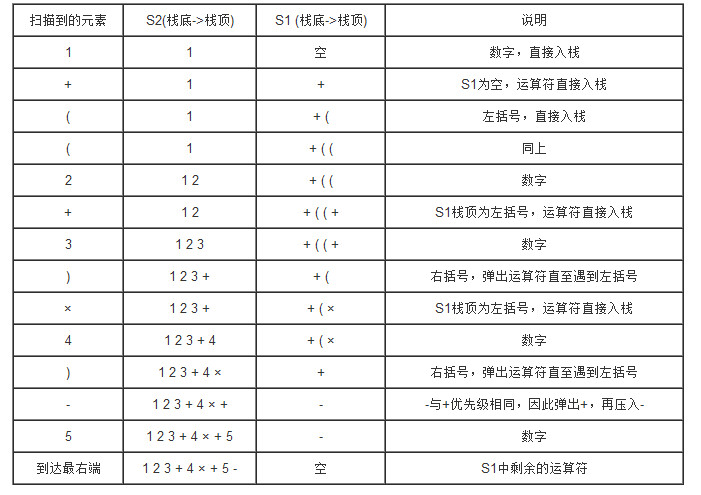
First, two stacks need to be allocated, one is stack S1 (including an end symbol) as a temporary storage operator, and the other is stack S2 (empty stack) as a storage result (inverse Polish). Stack S1 can be put into the operator with the lowest priority #. Note that infix should end with the operator with the lowest priority. Other characters can be specified, not necessarily # not required. Take characters from the left end of infix, and proceed to the following steps one by one:
- If the extracted character is an operand, the complete operand is analyzed, and the operand is directly sent to S2 stack.
- If the extracted character is an operator, compare the operator with the top element of S1 stack. If the priority of the operator (excluding the bracket operator) is higher than that of the top operator of S1 stack (including the left bracket), put the operator into S1 stack. Otherwise, pop up the top operator of S1 stack and put it into S2 stack until the top operator of S1 stack (including the left bracket) is lower than that of S1 stack (not including) stop popping the operator when it is equal to the priority of the operator, and finally send the operator to S1 stack.
- If the extracted character is "(", it will be directly sent to the top of S1 stack.
- If the extracted character is ")", the operators between "(" closest to the top of S1 stack will be out of the stack one by one and sent to S2 stack in turn. At this time, "(" will be discarded.
- Repeat steps 1 to 4 above until all input characters are processed.
- If the extracted character is "#", all operators in S1 stack (excluding "#") will be out of the stack one by one and sent to S2 stack in turn.
Calculation example
3, Infix to suffix, calculation and Implementation
public class testPolan {
public static void main(String[] args) {
String exp = "1+((12+0)*4)-5";
List<String> infixExpressionList = toInfixExpressionList(exp);
List<String> suffixExpressionList = parseSuffixExpressionList(infixExpressionList);
System.out.println("suffix List" + suffixExpressionList);
System.out.printf(exp + " = " + calculate(suffixExpressionList));
}
//Method: convert infix to suffix
public static List<String> parseSuffixExpressionList(List<String> ls) {
//Define two stacks
Stack<String> s1 = new Stack<String>();//Symbol stack
//Because there is no pop in s2 stack, it will be output in reverse order
//Therefore, it is troublesome. We use List2 directly
List<String> s2 = new ArrayList<String>();
//Traversal ls
for (String item : ls) {
//If it's a number, add s2
if (item.matches("\\d+")) {
s2.add(item);
} else if (item.equals("(")) {
s1.push(item);
} else if (item.equals(")")) {
while (!s1.peek().equals("(")) {
s2.add(s1.pop());
}
s1.pop();//Pop up parentheses
} else {
//The operator priority of item is less than or equal to the top of the stack
//The priority method is missing, see below
while (s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)) {
s2.add(s1.pop());
}
//You also need to push the item onto the stack
s1.push(item);
}
}
//Add the rest of s1 to s2
while (s1.size() != 0) {
s2.add(s1.pop());
}
return s2;
}
//Method: convert infix expression to corresponding List
public static List<String> toInfixExpressionList(String s) {
//First, define a list to store the data corresponding to the infix expression
List<String> ls = new ArrayList<String>();
int i = 0;//This is a pointer to traverse the infix expression string
String str;//Multi bit splicing
char c;//Each character traversed is put into c
do {
//If c is not a number, we add it to ls
if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
ls.add("" + c);
i++;
} else {
//Consider multi bit number
str = "";
while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
str += c;
i++;
}
ls.add(str);
}
} while (i < s.length());
return ls;
}
//Scan the expression from left to right. When encountering a number, push the number onto the stack
//When an operator is encountered, two numbers at the top of the stack are popped up and calculated
//Note the order: secondary top element - processing - > stack top element
//And put the result on the stack, and repeat the above process until the rightmost end of the expression
//The final result is the calculation result
public static int calculate(List<String> ls) {
Stack<String> stack = new Stack<String>();
//Traversal ls
for (String item : ls) {
if (item.matches("\\d+")) {
//Push
stack.push(item);
} else {
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
if (item.equals("+")) {
res = num1 + num2;
} else if (item.equals("-")) {
res = num1 - num2;
} else if (item.equals("*")) {
res = num1 * num2;
} else if (item.equals("/")) {
res = num1 / num2;
} else {
throw new RuntimeException("error");
}
stack.push(res + "");
}
}
return Integer.parseInt(stack.pop());
}
//Class: return priority number
static class Operation {
private static int ADD = 1;
private static int SUB = 1;
private static int MUL = 2;
private static int DIV = 2;
//Method to return the corresponding priority number
public static int getValue(String oper) {
int result = 0;
switch (oper) {
case "+":
result = ADD;
break;
case "-":
result = SUB;
break;
case "*":
result = MUL;
break;
case "/":
result = DIV;
default:
// System.out.println("unable to parse");
break;
}
return result;
}
}
}
4, Summary
Come on!