this article only uses two common implementation methods - dynamic array stack and chain queue. If you want to see more implementation methods of queue and stack, you can see the section on queue and stack in my following article: Figure 5 implementation of five interfaces，
   the queue and stack implementations in this article have been uploaded to the code cloud. You can pay attention to ~: My Gitee star will leave later

🎃 1, Stack

  stack is a last in first out structure. (LIFO)
   two implementations of comparison stack:

Array stack: use the head as the bottom of the stack and the tail as the top of the stack. The tail insertion and deletion efficiency is very high, and the waste of space doesn't matter. (with great advantages)

Chained stack: if you think it is the top of the stack, the efficiency of tail insertion and deletion is relatively low, and you need to implement a two-way linked list (otherwise you have to find the tail every time); If the head is used as the top of the stack and the head plug is deleted, the efficiency is very high. Although space is saved, the advantage is not obvious (the efficiency of entering and leaving the stack is no different from that of array stack).

  therefore, we chose to implement a dynamic array stack.

🗻 1. Storage structure and interface

  we use a dynamic array to store the elements in the stack. Top represents the subscript pointing to the next element at the top of the current stack (when the stack is empty, the value of top is 0), and capacity represents the size of the current stack.

typedef int StackDataType;
typedef struct {
	int top;
	StackDataType* arr;
	int capacity;
}Stack;
void StackInit(Stack* ps);
void StackPush(Stack* ps, StackDataType e);
void StackPop(Stack* ps);
StackDataType StackTop(Stack* ps);
int StackSize(Stack* ps);
bool StackEmpty(Stack* ps);
void Stackdestroy(Stack* ps);

🏟️ 2. Initialize stack

  initializing the stack is to set the top value of the stack to 0, capacity to 0 and arr to NULL.

void StackInit(Stack* ps)
{
	assert(ps);
	ps->capacity = 0;
	ps->arr = NULL;
	ps->top = 0;
	//Top means 0, which means pointing to the next position of the data at the top of the stack
	//ps->top = -1;
	//Top means - 1, which means it points to the data at the top of the stack
}

🏖️ 3. Stack

    because it is an array stack, we can query whether the space of the stack is enough before entering the stack, expand the capacity with realloc, insert e at the top of the array, and then top + +.

void checkcapacity(Stack* ps)
{
	if (ps->capacity == ps->top)
	{
		int newcapacity = (ps->arr == NULL ? 4 : 2 * ps->capacity);
		StackDataType* tmp = (StackDataType*)realloc(ps->arr, newcapacity*sizeof(StackDataType));
		if (tmp == NULL)
		{
			printf("realloc fault\n");
			exit(-1);
		}
		ps->arr = tmp;
		ps->capacity = newcapacity;
	}
}
void StackPush(Stack* ps, StackDataType e)
{
	assert(ps);
	checkcapacity(ps);
	ps->arr[ps->top] = e;
	ps->top++;
}

🕋 4. Judge whether the stack is empty

   if top==0, the stack is empty, otherwise the stack is not empty.

bool StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->top == 0;
	//return ps->top == -1;
}

🌁 5. Out of the stack

  first judge whether the stack is empty, and then top -.

void StackPop(Stack* ps)
{
	assert(ps && StackEmpty(ps) != true);
	ps->top--;
}

🚇 6. Return stack top element

  first check whether the stack is empty, and then return the element with the index of top in the array.

StackDataType StackTop(Stack* ps)
{
	assert(ps && StackEmpty(ps) != true);
	return ps->arr[ps->top - 1];
}

🎇 7. Determine the stack size

  just return the value of top.

int StackSize(Stack* ps)
{
	assert(ps);
	return ps->top;
}

🪂 8. Destroy queue

  free the applied arr, then set the ARR to NULL, and set both top and capacity to 0.

void Stackdestroy(Stack* ps)
{
	assert(ps);
	ps->top = 0;
	ps->capacity = 0;
	free(ps->arr);
	ps->arr = NULL;
}

🎢 2, Queue

  queue is a first in first out structure. (FIFO)
  there are many ways to implement this structure. Let's use C language to implement the chain queue without taking the lead.

🏰 1. Storage structure and interface

   since it is a chain queue, the idea is to follow the example of a single chain list, define a head pointer and a tail pointer, insert the head into the queue and delete the tail out of the queue. Specifically, the structure of our queue and the interfaces to be implemented are as follows:

typedef int QDataType;
typedef struct QueueNode {
	QDataType data;
	struct QueueNode* next;
}QNode;
typedef struct {
	QNode* head;
	QNode* tail;
}Queue;
//Chain queue without sentry position
void QueueInit(Queue* pq);
bool QueueEmpty(Queue* pq);
void QueuePush(Queue* pq, QDataType e);
void QueuePop(Queue* pq);
QDataType Queuefront(Queue* pq);
QDataType Queueback(Queue* pq);
int QueueSize(Queue* pq);
void Queuedestroy(Queue* pq);

🕍 2. Initialize chain queue

    for the chain queue without the lead node, the task to be completed in initialization is to set both the head and tail empty, indicating that the current queue is empty and convenient for subsequent insertion.

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}

🌇 3. Judge whether the queue is empty

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}

🎡 4. Queue

   similar to the tail insertion of single linked list, special attention should be paid to the case that the single linked list is empty.

void QueuePush(Queue* pq, QDataType e)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc fault\n");
		exit(-1);
	}
	newnode->data = e;
	newnode->next = NULL;
	if (QueueEmpty(pq) == true)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}

🛕 5. Out of queue

   the queue is similar to the header deletion of a single linked list. Note that when deleting the last element of the queue, both tail and head should be empty at the same time, and note that if the queue is empty, it should not be deleted again.

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->tail == pq->head)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}

🌅 6. Number of queue elements

   there are two implementation methods. One is to add an unsigned integer variable size to the queue structure to represent the queue size. Each time, enter the queue size + +, and exit the queue size –; The other is our following implementation method, which traverses the queue and returns the queue length with a counter.

int QueueSize(Queue* pq)
{
	assert(pq);
	int count = 0;
	QNode* cur = pq->head;
	while (cur)
	{
		cur = cur->next;
		count++;
	}
	return count;
}

🍔 7. Return the first and last elements of the queue

    this is simple. Just return the elements indicated by head and tail. Pay attention to checking whether the queue is empty.

QDataType Queuefront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}
QDataType Queueback(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}

🥙 8. Destroy queue

   just follow the destruction of single linked list.

void Queuedestroy(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
}

🍝 3, OJ exercise

🎂 1.leetcode 20. Valid parentheses

🥧 Title Description

🥛 thinking

This bracket matching problem can be realized by stack.
Paste all our code about the stack (if you use cpp, you can use the stack in the STL library).
Create a stack,
The left bracket is pushed into the stack;
The right bracket is out of stack matching;
Finally, check whether the stack is empty;
If you encounter the right bracket as soon as you come up, that is to say, you think of the stack as empty as soon as you come up;
Then return false
Remember to destroy our stack before each return.

🧊 code

bool isValid(char * s)
{
    //Idea: enter the stack in case of left parenthesis
    //Right bracket out of stack match encountered
    //Finally, check whether the stack is empty
    //If you come up with a right parenthesis, that is, you come up with an empty stack
    //Then return false
    Stack st;
    StackInit(&st);
    while(*s)
    {
        if(*s == '(' || *s == '[' || *s == '{')
        {
            StackPush(&st, *s);
            s++;
        }
        if(*s == '}' || *s == ')' || *s == ']')
        {
            if(StackEmpty(&st)==true)
            {
                Stackdestroy(&st);
                return false;
            }
            StackDataType x = StackTop(&st);
            StackPop(&st);
            if((*s == '}' && x != '{') || (*s == ']' && x != '[') || (*s == ')' && x != '('))
            {
                Stackdestroy(&st);
                return false;
            }
            s++;
        }
    }
    if (StackEmpty(&st) == true)
    {
        Stackdestroy(&st);
        return true;
    }
    else
    {
        Stackdestroy(&st);
        return false;
    }
}

🍛 2.leetcode 225. Implementing stack with queue

🍿 Title Description

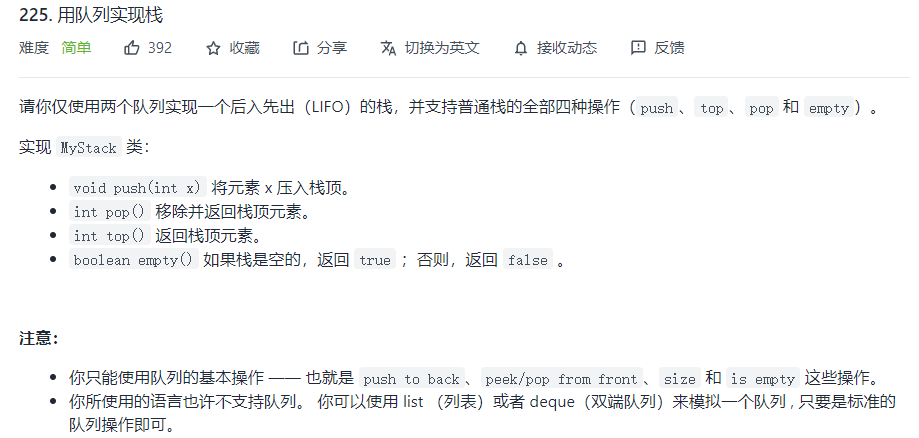
🍙 thinking

  use two queues to realize stack;

1. If you want to enter the stack, select an empty queue to be listed in the queue;
2. If you want to get out of the stack, put all the elements in the non empty queue except the last element into another empty queue, and pop up the original non empty queue element every time you enter an element, and then let the last element out of the queue to end the process of getting out of the queue;
3. If you want to return the top element of the stack, you can return the tail element of the non empty queue;
4. To determine which queue is empty, you can use the QueueEmpty function. First, assume that one queue is empty and the other queue is not empty, and then judge whether the queue is empty. If it is empty, it means that the assumption is correct and there is no need to exchange. If it is not empty, it means that the assumption is wrong and the other queue is not empty;
5. Whether the stack is empty depends on whether both queues are empty.
6. If you want to destroy the stack, destroy two queues, and then free the pointer of the stack.

🍲 code

//Idea: use two queues to realize the stack. When entering the stack, let the elements join a queue;
//To get out of the stack, add all but the last element in the queue to another queue, and remove the last element from the original queue
//To view the top element of the stack, first add all but the last element in the non empty queue to another queue, and then return the last element 
//Then add this element to another queue to make the original queue empty

typedef struct {
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() {
    MyStack* st = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&st->q1);
    QueueInit(&st->q2);
    return st;
}

void myStackPush(MyStack* obj, int x) {
    Queue* emptyQ = &obj->q1;
    Queue* inemptyQ = &obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        emptyQ = &obj->q2;
        inemptyQ = &obj->q1;
    }
    QueuePush(inemptyQ, x);
}

int myStackPop(MyStack* obj) {
    Queue* emptyQ = &obj->q1;
    Queue* inemptyQ = &obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        emptyQ = &obj->q2;
        inemptyQ = &obj->q1;
    }
    while (QueueSize(inemptyQ)>1)
    {
        QueuePush(emptyQ, Queuefront(inemptyQ));
        QueuePop(inemptyQ);
    }
    int ret = Queuefront(inemptyQ);
    QueuePop(inemptyQ);
    return ret;
}

int myStackTop(MyStack* obj) {
    if (QueueEmpty(&obj->q1) == true)
    {
        return Queueback(&obj->q2);
    }
    else
    {
        return Queueback(&obj->q1);
    }
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1) == true && QueueEmpty(&obj->q2) == true;
}

void myStackFree(MyStack* obj) {
    Queuedestroy(&obj->q1);
    Queuedestroy(&obj->q2);
    free(obj);
}

🍦 3.leetcode 232. Realizing queue with stack

🏟️ Title Description

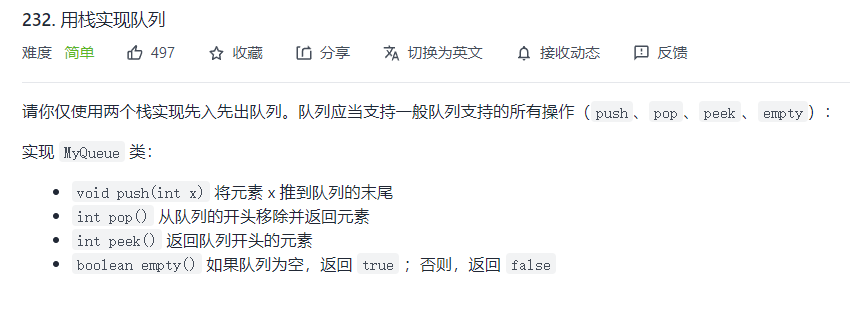
🏖️ thinking

   two stacks are used to realize the queue. One stack is responsible for the queue entry operation, which is recorded as pushST, and the other stack is responsible for the queue exit operation, which is recorded as popST.

1. When entering the queue, enter the pushST stack.
2. When leaving the queue, first judge whether the popST stack is empty. If it is empty, put all the elements of popST into the pushST stack, and then pop up the top elements of popST and return.
3. To return the first element of the queue, change the pop-up stack top element to return the stack top element in the out of queue operation.
4. Whether the queue is empty depends on whether the two stacks are empty.
5. Destroying the queue destroys two stacks, and then free drops the pointer to the queue.

🪂 code

typedef struct {
    Stack pushST;
    Stack popST;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* q = (MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&q->pushST);
    StackInit(&q->popST);
    return q;
}

void myQueuePush(MyQueue* obj, int x) {
    StackPush(&obj->pushST, x);
}

int myQueuePop(MyQueue* obj) {
    if (StackEmpty(&obj->popST))
    {
        while (!StackEmpty(&obj->pushST))
        {
            StackPush(&obj->popST, StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
    }
    int ret = StackTop(&obj->popST);
    StackPop(&obj->popST);
    return ret;
}

int myQueuePeek(MyQueue* obj) {
    if (StackEmpty(&obj->popST))
    {
        while (!StackEmpty(&obj->pushST))
        {
            StackPush(&obj->popST, StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
    }
    int ret = StackTop(&obj->popST);
    return ret;
}

bool myQueueEmpty(MyQueue* obj) {
    return StackEmpty(&obj->pushST) && StackEmpty(&obj->popST);
}

void myQueueFree(MyQueue* obj) {
    Stackdestroy(&obj->pushST);
    Stackdestroy(&obj->popST);
    free(obj);
}

🏟️ 4.leetcode 622. Design cyclic queue

🎇 Title Description

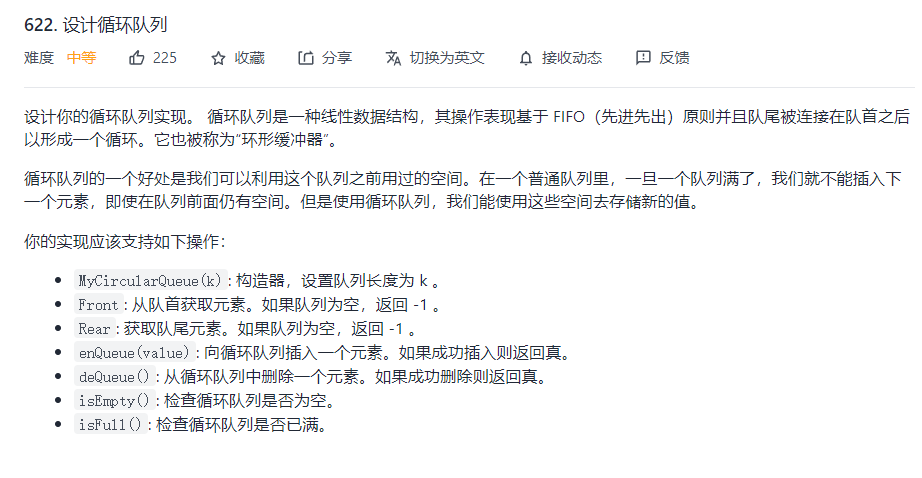
✨ thinking

   the key of circular queue is to vacate a position to distinguish between empty queue and full queue. Otherwise, when the queue is full, the pointer at the head and tail of the queue will coincide because it is a circular queue. However, during initialization, front and rear coincide, which makes it impossible to distinguish between empty and full queues.

🍛 Idea 1: array to achieve circular queue

   the key to realizing circular queue in array is to use% to return the front and rear values beyond the size range of the array to the array.

1. If the queue has k elements, apply for space of k+1 elements
2. Queue empty front == rear
3. Queue full (rear+1)%(k+1) == front
4. When the element E is queued, the element referred to by rear becomes e, then rear + +, and then rear%(k+1) returns to the array range.
5. Out of the queue is front + +, and then front%(k+1) returns to the array range.
6. When the first element of the queue is returned, the element with the subscript front of the array is returned.
7. When the end of the queue element is returned, the elements of the array with the following subscripts are returned (if you want to use%, draw a diagram to figure it out):
   i = ( o b j − > r e a r + o b j − > s i z e ) % ( o b j − > s i z e + 1 ) i = (obj->rear + obj->size)\%(obj->size + 1) i=(obj−>rear+obj−>size)%(obj−>size+1)
   Or when the rear is equal to 0, its predecessor is the k-th element.
8. Destroy the circular queue array, and then free the pointer to the circular queue.

🏰 code

typedef struct {
    int* a;
    int size;
    int front;
    int rear;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* cq = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    cq->a = (int*)malloc((k+1)*sizeof(int));
    cq->size = k;
    cq->front = cq->rear = 0;
    return cq;
}
bool myCircularQueueIsFull(MyCircularQueue* obj);
bool myCircularQueueIsEmpty(MyCircularQueue* obj);

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    obj->a[obj->rear] = value;
    obj->rear++;
    obj->rear %= (obj->size + 1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    obj->front++;
    obj->front %= (obj->size + 1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    //rear does not refer to the tail element, but the latter element of the tail element needs to be processed
    int i = (obj->rear + obj->size)%(obj->size + 1);
    return obj->a[i];
    //Or deal with it like this
    //if (obj->rear == 0)
    //{
    //    return obj->a[obj->size];
    //}
    //return obj->a[obj->rear - 1];
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->rear == obj->front;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear + 1)%(obj->size + 1) == obj->front;
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

🎢 Idea 2: realize circular queue with single linked list

1. When creating a circular queue, if the queue has a space of k+1 elements, apply for a space of k+1 elements. Use head to remember the address of this space for subsequent destruction, and then connect the next values of these nodes. The next value of the last node points to the first node, and then define a head pointer, tail pointer and current queue size.
2. Whether the queue is empty depends on whether front and rear are equal.
3. Whether the queue is full depends on whether the next of rear is equal to front.
4. Enter the queue to judge whether the queue is full. If it is dissatisfied, enter rear - > data = e, and then enter rear = rear - > next.
5. Out of the queue, check whether the queue is empty. If not, front = front - > next
6. When you return the first element of the queue, judge whether the queue is empty. If it is not empty, return front - > data;
7. When returning the end of the queue element, judge whether the queue is empty. If it is not empty, return real - > data;
8. When the queue is destroyed, the head is free, and then the pointer to the queue is free.

🎇 code

typedef struct Node{
    int data;
    struct Node* next;
}Node;

typedef struct {
    Node* front;
    Node* rear;
    Node* head;
    int size;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* cq = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    cq->size = k;
    cq->front = (Node*)malloc((k+1)*sizeof(Node));
    Node* tmp = cq->front;
    for (int i = 1; i <= k; i++)
    {
        tmp->next = tmp + 1;
        tmp = tmp->next;
    }
    tmp->next = cq->front;
    cq->rear = cq->front;
    cq->head = cq->front;
    return cq;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj);

bool myCircularQueueIsFull(MyCircularQueue* obj);

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if (myCircularQueueIsFull(obj))
    {
        return false;
    }
    obj->rear->data = value;
    obj->rear = obj->rear->next;
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    obj->front = obj->front->next;
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->front->data;
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    Node* cur = obj->front;
    while (cur->next != obj->rear)
    {
        cur = cur->next;
    }
    return cur->data;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return obj->rear->next == obj->front;
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->head);
    free(obj);
}

   by comparing the two ideas, it can be found that although the structure and creation of the single linked list implementation are somewhat complex, the queue in operation, queue out operation, judging whether the queue is empty, judging whether the queue is full, returning the first element of the queue and returning the last element of the queue are much simpler than the array implementation.