Insert sort idea

When sorting, each element to be sorted is compared with the previous sorted element. If the reverse order occurs, you need to find a suitable position in the sorted element sequence that can keep it in order, find the insertion position, move the sorted sequence back to make space, and then insert the elements to be sorted;

Specific description: for an array A[N], when the ith element (I > = 1) is inserted, the preceding A[0], A[1],..., A[i-1] is the ordered element sequence. When comparing A[i] with A[i-1], if the reverse order occurs, you need to find the insertion position K (where 0 < = k < i-1) in the ordered element sequence. After finding A[k], A[k+1],..., A[i-1] move backward in turn, The position of A[k] is replaced by A[i]

Algorithm steps

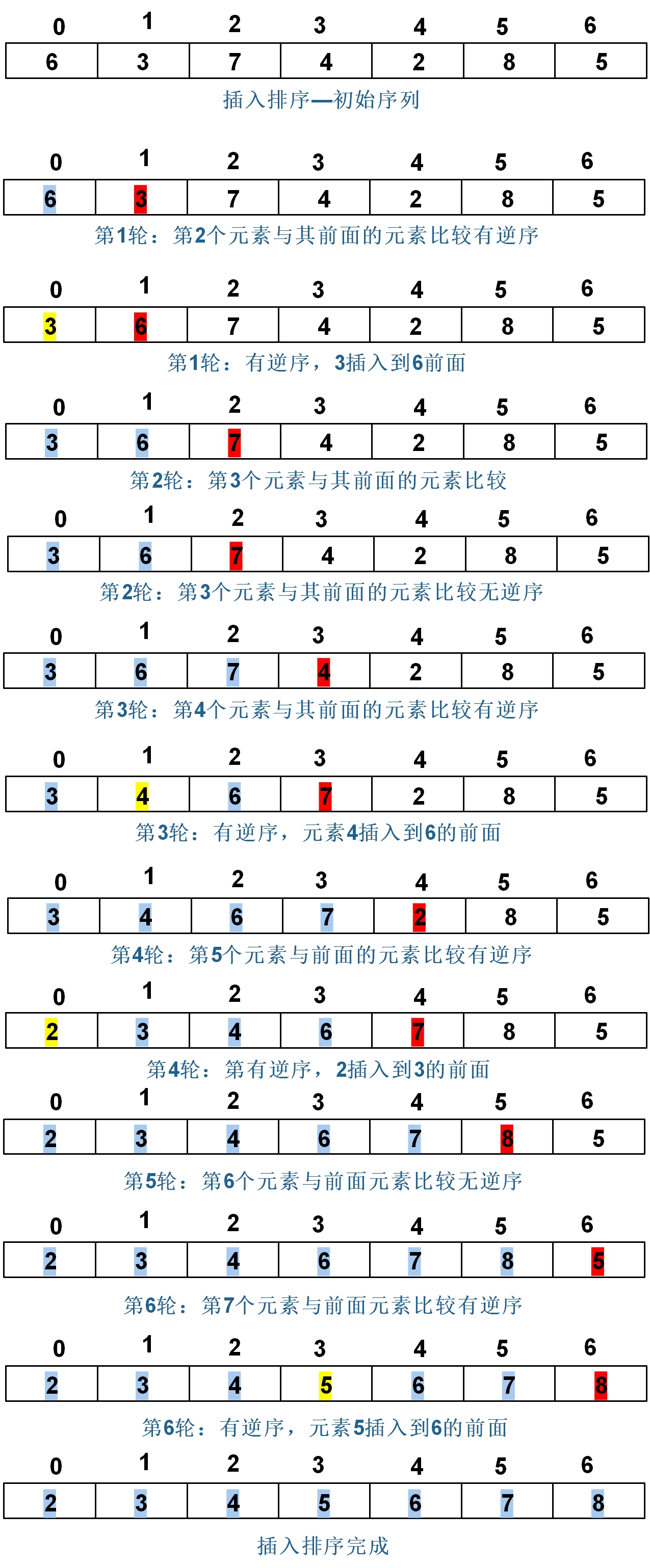
Take the insertion sorting process of an ordinary array A[N] from small to large as an example:

Round 1: compare A[0] with A[1]. If there is reverse order, insert it in front of the first element, and move it twice at worst to form a sequence of 2 sorted elements

Round 2: compare A[1] with A[2]. If there is reverse order, find a position to insert in the sequence of 2 ordered elements, and move it for 3 times at the worst to form a sequence of 3 ordered elements

Round 3: compare A[2] with A[3]. Similarly, if there is reverse order, find a position to insert in the sequence of 3 ordered elements, and move it 4 times at the worst to form a sequence of 4 sorted elements

Round N-1: comparing A[N-2] with A[N-1], the worst case is to move N times to form N ordered element sequences, and the sorting is completed

The initial sequence given in the following figure is taken as an example, and the results of each round of sorting are shown in the figure:

Time complexity

Ideally, the initial sorting element sequence has been ordered. Each round only needs to be compared with the last element of the previous ordered element sequence. The total number of comparisons is n-1 and the number of element moves is 0;

Worst case: when the elements to be sorted are in reverse order, the i-th element must be compared with the previous I-Elements, and the data must be moved every comparison

The total number of comparisons is: ∑ i = 1 n − 1 i = 1 + 2 + 3 + . . . + ( n − 1 ) = n ( n − 1 ) 2 ≈ n 2 2 \sum_{i=1}^{n-1} i= 1+2+3+...+(n-1) = \frac{n(n-1)}{2} \approx \frac{n^2}{2} i=1∑n−1​i=1+2+3+...+(n−1)=2n(n−1)​≈2n2​

The total number of moves is: ∑ i = 1 n − 1 ( i + 1 ) = 2 + 3 + . . . + n = ( n − 1 ) ( n + 2 ) 2 ≈ n 2 2 \sum_{i=1}^{n-1} (i+1)= 2+3+...+n = \frac{(n-1)(n+2)}{2} \approx \frac{n^2}{2} i=1∑n−1​(i+1)=2+3+...+n=2(n−1)(n+2)​≈2n2​

Therefore, the total time complexity is o( n 2 n^2 n2), and direct insertion sorting is A stable sorting algorithm, that is, two identical elements A and A 'in the original sequence,

If A is in front of A ', the relative order of A and A' remains unchanged after sorting

Insert sorting source code

#include <stdio.h>
#include <stdlib.h>

//Insert sort: sort from small to large
void insertSort(int arr[], int n) {
  int val;
  for (int i = 1; i < n; i++) {
    //If the latter element is smaller than the previous element
    if (arr[i] < arr[i - 1]) {
      val = arr[i];
      int j = i - 1;
      do {
        arr[j + 1] = arr[j];
        j--;
      } while (j >= 0 && val < arr[j]);
      arr[j + 1] = val;
    }
  }
}
int output(int arr[], int n) {
  for (int i = 0; i < n; i++) {
    printf("%d, ", arr[i]);
  }
  printf("\n");
}

int main() {
  // int arr[] = {6, 3, 7, 4, 2, 8, 5};
  int arr[] = {2, 5, 6, 7, 1, 4, 8, 9};
  // int arr[] = {1};
  int n = sizeof(arr) / sizeof(int);
  insertSort(arr, n);
  output(arr, n);
  return 0;
}

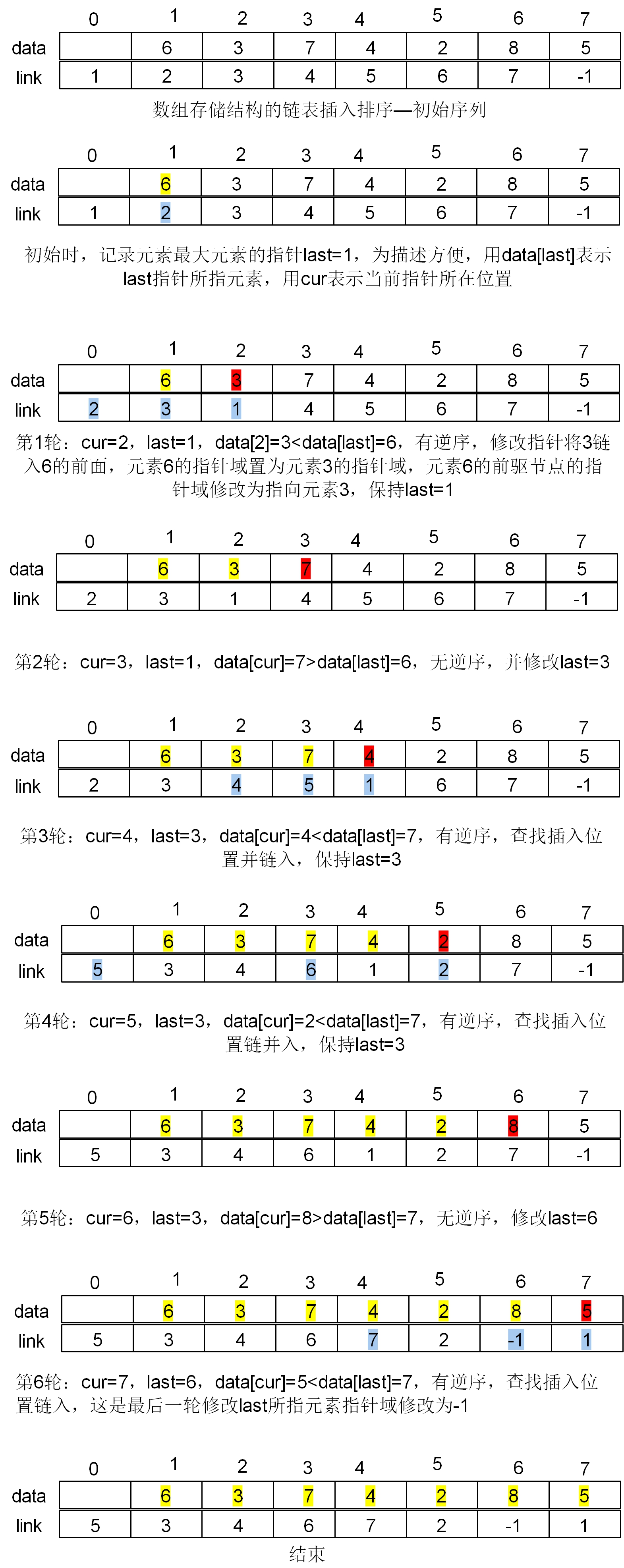
Linked list of array storage structure - insert sort

For the linked list insertion sorting of array storage structure, the element insertion is realized by modifying the pointer field of the element, and there is no need to move the data field, which avoids the defect of moving elements in batch when inserting and sorting ordinary arrays. It has relatively high efficiency. When the comparison times are still the same as that of ordinary arrays

The following is a linked list based on array storage structure. The specific sorting process is illustrated as follows:

Linked list of array storage structure - insert sorting source code

#include <stdio.h>
#include <stdlib.h>

struct Element {
  //Data domain
  int data;
  //Pointer
  int link;
};

//Encapsulate Element related properties
struct StaticList {
  int maxSize;
  // elements[0] is an additional header node
  // int *p;
  struct Element *elements;
  // The tail pointer points to the last element added to facilitate tail insertion
  int tail;
  // The avail able pointer points to the first position of the standby linked list
  int avail;
  // Indicates the number of current elements
  int currentSize;
};

int initStaticList(struct StaticList *p, int maxSize) {
  p->avail = 1;
  p->tail = 0;
  p->currentSize = 0;
  p->maxSize = maxSize > 10 ? (maxSize + 1) : 10;
  p->elements = (struct Element *)malloc(p->maxSize * sizeof(struct Element));
  for (int i = 1; i < p->maxSize; i++) {
    p->elements[i].link = i + 1;
  }
  p->elements[0].link = -1;
  p->elements[maxSize].link = -1;
}

void addElement(struct StaticList *p, int x) {
  int cur = p->avail;
  if (cur == -1) {
    printf("memory overflow");
    return;
  }
  p->avail = p->elements[cur].link;
  p->elements[cur].data = x;
  //The pointer field of the newly inserted element is - 1
  p->elements[cur].link = -1;
  p->elements[p->tail].link = cur;
  p->tail = cur;
  p->currentSize++;
}
void output(struct Element *ems) {
  int cur = ems[0].link;
  while (cur != -1) {
    printf("%d, ", ems[cur].data);
    cur = ems[cur].link;
  }
  printf("\n");
}

//Static linked list insertion sorting, from small to large
void insertSortElement(struct Element ems[]) {
  int ptr = ems[0].link;
  if (ptr == -1 || ems[ptr].link == -1) {
    return;
  }
  ptr = ems[ptr].link;
  // last records the pointer to the largest element
  int last = ems[0].link;
  // Pre and cur are pointers to the front and back nodes of the inner loop respectively
  int pre, cur;
  // ptr is used as the pointer of the outer loop, and nextptr is used as the pointer of the successor node of ptr
  int nextptr;
  while (ptr != -1) {
    pre = 0;
    cur = ems[0].link;
    //To achieve from large to small, modify to EMS [cur] data > ems[ptr]. data
    while (ems[cur].data < ems[ptr].data) {
      pre = cur;
      cur = ems[cur].link;
    }
    //Temporary EMS [PTR] Link pointer, otherwise it will be overwritten
    nextptr = ems[ptr].link;
    // The cur pointer does not point to ptr, indicating that there is an insert
    if (cur != ptr) {
      // Subsequent nodes of ptr point to cur
      ems[ptr].link = cur;
      // Subsequent nodes of pre point to ptr
      ems[pre].link = ptr;
      //The pointer field of the updated maximum element points to the latest node. If nextptr is the last node, take - 1
      ems[last].link = nextptr;
    } else {
      //If the elements are already ordered, the current pointer ptr is recorded as the pointer of the largest element
      last = ptr;
    }
    ptr = nextptr;
  }
}

int main() {
  struct StaticList p;
  int arr[] = {1, 4, 6, 7, 0, 3, 10, 9, 2, 9,
               3, 7, 4, 8, 5, 6, 1, 0, 9999, 44,
               9999, 2, 4, 9, 4, 12, 44, 99, -1, 0,
               5, 888, 345, 12344, 5555, 9090, 10000, 123, 444, -888,
               100, 400, 120000, 899999, -1, -2, 8, 9, 8};
  // int arr[]={6,4,3,8,7,5,2,1};
  // int arr[] = {2, 5, 6, 7, 1, 4, 8, 9};
  // int arr[] = {9, 0};
  int n = sizeof(arr) / sizeof(int);
  initStaticList(&p, n);
  for (int i = 0; i < n; i++) {
    addElement(&p, arr[i]);
  }
  printf("#### insert sort before ####\n");
  output(p.elements);
  printf("#### insert sort after ####\n");
  insertSortElement(p.elements);
  output(p.elements);
  free(p.elements);
  return 0;
}