 Rimeng Society
Rimeng Society
AI AI:Keras PyTorch MXNet TensorFlow PaddlePaddle deep learning real combat (irregular update)
Integrated learning: Bagging, random forest, Boosting, GBDT
Integrated learning: lightGBM (I)
Integrated learning: lightGBM (II)
5.1 principle of xgboost algorithm
XGBoost (Extreme Gradient Boosting) is fully called extreme gradient lifting tree. XGBoost is the trump card of integrated learning method. In Kaggle data mining competition, most winners use XGBoost.
XGBoost performs very well in most regression and classification problems. This section will introduce the algorithm principle of XGBoost in detail.
1. Construction method of optimal model
As we have known before, the general method of constructing the optimal model is to minimize the loss function of training data.
We use the letter L to represent the loss, as follows:
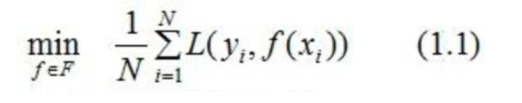
Where F is the hypothetical space
Hypothesis space is a set of assumptions without omission for all cases that may meet the goal when the attributes and possible values of attributes are known.
Equation (1.1) is called empirical risk minimization, and the complexity of the trained model is high. When the training data is small, the model is prone to over fitting problems.
Therefore, in order to reduce the complexity of the model, the following formula is often used:
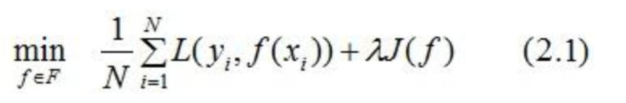
Where J(f)J(f) is the complexity of the model,
Equation (2.1) is called structural risk minimization. The model of structural risk minimization often has a good prediction of training data and unknown test data.
Application:
- The generation and pruning of decision tree correspond to empirical risk minimization and structural risk minimization respectively,
- The decision tree generation of XGBoost is the result of structural risk minimization, which will be described in detail later.
2. Derivation of objective function of xgboost
2.1 determination of objective function
The objective function, namely the loss function, constructs the optimal model by minimizing the loss function.
It can be seen from the above that the loss function should be added with a regular term representing the complexity of the model, and the model corresponding to XGBoost contains multiple CART trees. Therefore, the objective function of the model is:
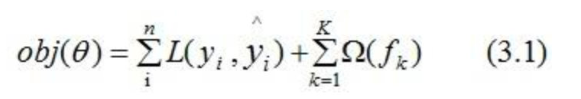

2.2 introduction to cart tree
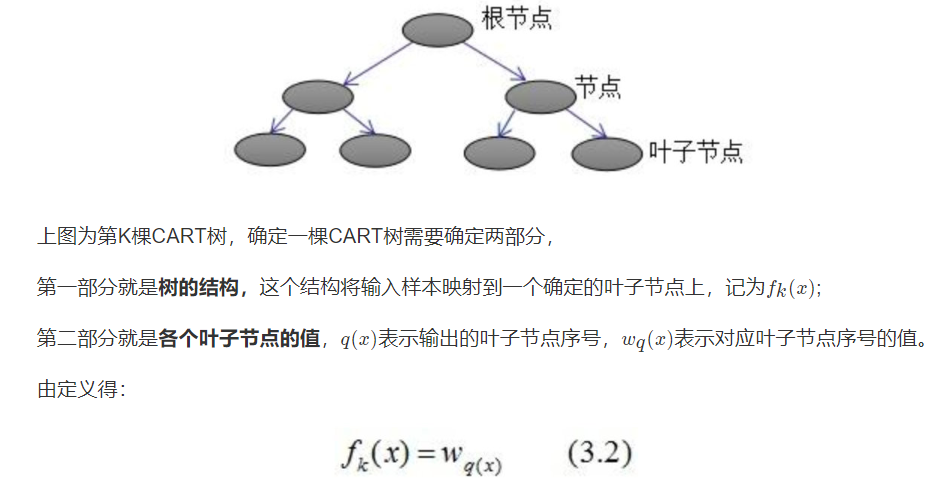
2.3 definition of tree complexity
2.3. 1 define the complexity of each lesson tree
The model corresponding to XGBoost method contains multiple cart trees, and the complexity of each tree is defined:

2.3. 2 example of tree complexity
Suppose we want to predict the family's preference for video games. Considering that young people are more likely to like video games than old people, and men prefer video games than women, we first distinguish children and adults according to their age, and then distinguish men and women by gender, and score each person's preference for video games one by one, As shown in the figure below:
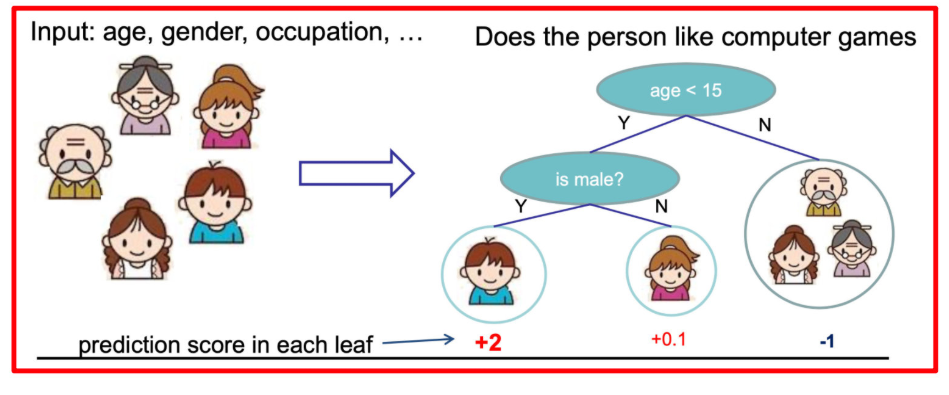
In this way, two trees tree1 and tree2 are trained. Similar to the principle of gbdt before, the sum of the conclusions of the two trees is the final conclusion, so:
- The predicted score of the little boy is the sum of the scores of the nodes where the child falls in the two trees: 2 + 0.9 = 2.9.
- Grandpa's prediction score is the same: - 1 + (- 0.9) = - 1.9.
See the following figure for details: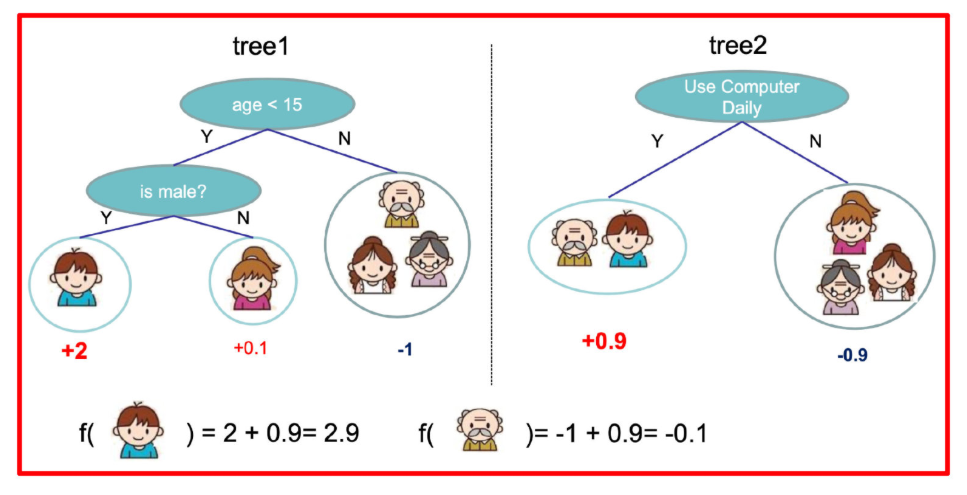
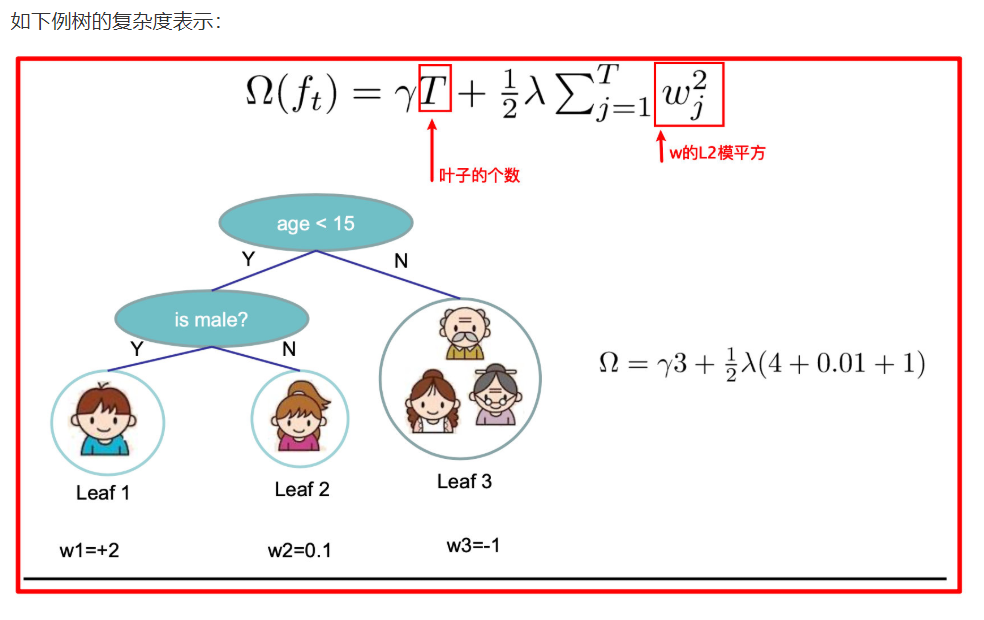
2.4 derivation of objective function


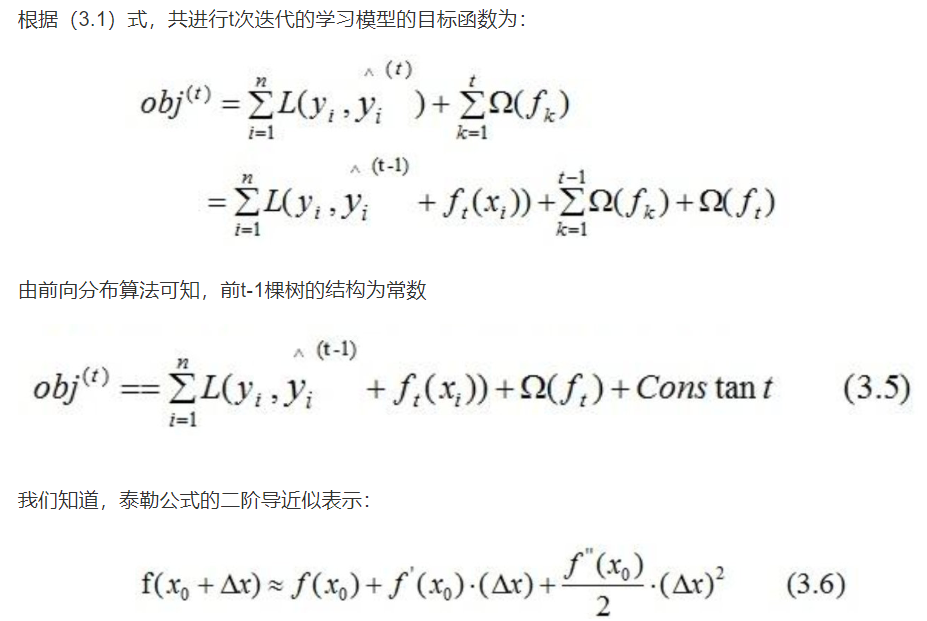



3 regression tree construction method of xgboost
3.1 calculating split nodes
In the actual training process, when the t-th tree is established, XGBoost uses the greedy method to split the tree nodes:
Start when the tree depth is 0:
-
Try to split each leaf node in the tree;
-
After each split, the original leaf node continues to split into left and right child leaf nodes, and the sample set in the original leaf node will be dispersed into the left and right leaf nodes according to the judgment rules of the node;
-
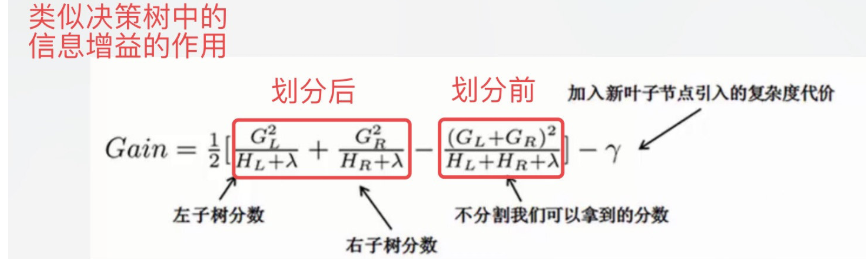
After splitting a new node, we need to check whether this splitting will bring gain to the loss function. The definition of gain is as follows:
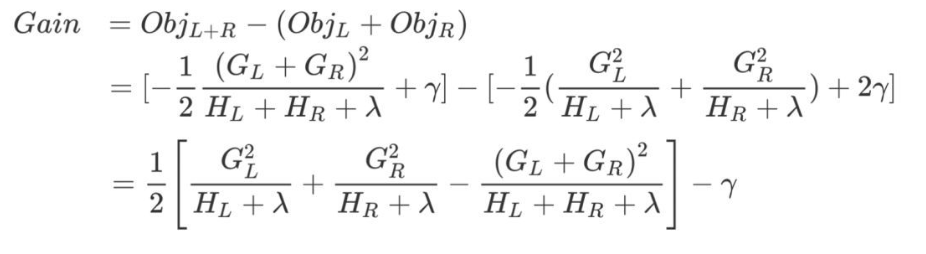
If gain > 0, that is, after splitting into two leaf nodes, the objective function decreases, then we will consider the result of this splitting.
So when will the division stop?
3.2 judgment of stop splitting conditions
Case 1: the scoring function derived in the previous section is the standard to measure the tree structure. Therefore, the scoring function can be used to select the best segmentation point. Firstly, determine all the segmentation points of the sample characteristics, and segment each determined segmentation point. The criteria for segmentation are as follows:

4. Difference between xgboost and GDBT
- Difference 1:
- XGBoost generates CART tree considering the complexity of the tree,
- GDBT does not consider the complexity of the tree in the tree pruning step.
- Difference 2:
- XGBoost is the second derivative expansion fitting the loss function of the previous round, and GDBT is the first derivative expansion fitting the loss function of the previous round. Therefore, XGBoost has higher accuracy, meets the same training effect, and requires fewer iterations.
- Difference 3:
- Both XGBoost and GDBT iterate step by step to improve the performance of the model, but XGBoost can start multithreading when selecting the best segmentation point, which greatly improves the running speed.
5 Summary

5.2 introduction to xgboost algorithm api
1 xgboost installation:
Official website link: https://xgboost.readthedocs.io/en/latest/
pip3 install xgboost
2. Introduction to xgboost parameters
Although xgboost is called the kaggle game, if we want to train a good model, we must pass appropriate values to the parameters.
xgboost encapsulates many parameters, which are mainly composed of three types: general parameters, booster parameters and task parameters
- General parameters: mainly macro function control;
- Booster parameter: depending on the selected booster type, it is used to control the booster (tree, region) of each step;
- Learning goal parameters: control the performance of training goals.
2.1 general parameters
- booster [default = gbtree]
-
Decide which booster to use. It can be gbtree, gblinear or dart.
- gbtree and dart use tree based models (DART mainly uses Dropout), while gblinear uses linear functions
-
silent [default = 0]
- Set to 0 to print operation information; Set to 1 silent mode, do not print
-
nthread [default = set to maximum possible number of threads]
- For the number of threads running xgboost in parallel, the input parameter should be < = the number of CPU cores of the system. If it is not set, the algorithm will detect and set it to all the cores of the CPU
The following two parameters do not need to be set. Just use the default
-
num_pbuffer [xgboost is automatically set, no user setting is required]
- The size of the prediction result cache is usually set to the number of training instances. This cache is used to store the prediction results of the last boosting operation.
-
num_feature [xgboost is automatically set, no user setting is required]
- Use the dimension of the feature in boosting and set it as the maximum dimension of the feature
2.2 booster parameters
2.2.1 Parameters for Tree Booster
-
eta [default = 0.3, alias: learning_rate]
-
Reduce the step size in the update to prevent overfitting.
-
After each boosting, new feature weights can be obtained directly, which can make the boosting more robust.
- Range: [0,1]
-
-
gamma [default = 0, alias: min_split_loss]
- When a node is split, it will split only when the value of the loss function decreases after splitting.
-
Gamma specifies the minimum loss function drop value required for node splitting. The larger the value of this parameter, the more conservative the algorithm is. The value of this parameter is closely related to the loss function, so it needs to be adjusted.
-
Range: [0, ∞]
-
max_depth [default = 6]
- This value is the maximum depth of the tree. This value is also used to avoid over fitting. max_ The greater the depth, the more specific and local samples the model will learn. Setting to 0 means there is no limit
- Range: [0, ∞]
-
min_child_weight [default = 1]
- Determine the minimum leaf node sample weight and. This parameter of XGBoost is the sum of the minimum sample weights
- When its value is large, the model can avoid learning local special samples. However, if this value is too high, it will lead to under fitting. This parameter needs to be adjusted using CV
- Range: [0, ∞]
-
subsample [default = 1]
- This parameter controls the proportion of random sampling for each tree.
-
Reducing the value of this parameter will make the algorithm more conservative and avoid over fitting. However, if this value is set too small, it may result in under fitting.
-
Typical value: 0.5-1, 0.5 represents average sampling to prevent over fitting
- Range: (0,1]
-
colsample_bytree [default = 1]
- It is used to control the proportion of the number of columns sampled randomly per tree (each column is a feature).
- Typical value: 0.5-1
- Range: (0,1]
-
colsample_bylevel [default = 1]
- It is used to control the sampling proportion of the number of columns for each split of each level of the tree.
- Personally, I don't use this parameter because the subsample parameter and colsample parameter_ The bytree parameter can do the same. However, if you are interested, you can mine this parameter for more use.
- Range: (0,1]
-
Lambda [default = 1, alias: reg_lambda]
- L2 regularization term of weight (similar to ridge expression).
- This parameter is used to control the regularization part of XGBoost. Although most data scientists rarely use this parameter, this parameter
- We can find more use in reducing over fitting
-
Alpha [default = 0, alias: reg_alpha]
- L1 regularization term of weight. (similar to lasso region). It can be applied in the case of high dimensions to make the algorithm faster.
-
scale_pos_weight [default = 1]
- When all kinds of samples are very unbalanced, setting this parameter to a positive value can make the algorithm converge faster. You can usually set it to negative
- The ratio of the number of samples to the number of positive samples.
2.2.2 Parameters for Linear Booster
linear booster is rarely used.
-
Lambda [default = 0, alias: reg_lambda]
- L2 regularization penalty coefficient. Increasing this value will make the model more conservative.
-
Alpha [default = 0, alias: reg_alpha]
- L1 regularization penalty coefficient. Increasing this value will make the model more conservative.
-
lambda_ Bias [default = 0, alias: reg_lambda_bias]
- L2 regularization on bias (no bias on L1 because it is not important)
2.3 task parameters
-
objective [default = reg:linear]
- "reg:linear" – linear regression
- "reg:logistic" – logistic regression
- "binary:logistic" – binary logistic regression with probability output
- "multi:softmax" – use softmax's multi classifier to return the predicted category (not probability). In this case, you also need to set one more parameter: num_ Class (number of categories)
- "multi:softprob" – the same as the multi:softmax parameter, but returns the probability that each data belongs to each category.
-
eval_metric [default = selected by objective function]
The options are as follows:
- "rmse": root mean square error
- "mae": mean absolute error
- "logloss": negative log likelihood function value
- "Error": secondary classification error rate.
- Its value is obtained by the ratio of the number of wrong classifications to the number of all classifications. For the prediction, the prediction value greater than 0.5 is considered as positive, and others are classified as negative.
- “ error@t ”: different division thresholds can be set through't '
- "merror": multi category error rate. The calculation formula is (wrong cases)/(all cases)
- "mlogloss": multi category log loss
- "auc": area under curve
-
seed [default = 0]
- Seed of random number
- Set it to reproduce the results of random data and adjust parameters
5.3 xgboost case introduction
1 case background
This case is the same as the case used in the previous decision tree.
The sinking of the Titanic is one of the most notorious shipwrecks in history. On April 15, 1912, during her maiden voyage, the Titanic sank after colliding with an iceberg, killing 1502 of 2224 passengers and crew. This sensational tragedy shocked the international community and formulated better safety regulations for ships. One of the reasons for the shipwreck is that the passengers and crew did not have enough lifeboats. Although there are some luck factors in survival and sinking, some people are easier to survive than others, such as women, children and upper class society. In this case, we ask you to complete the analysis of who is likely to survive. In particular, we ask you to use machine learning tools to predict which passengers survived the tragedy.
Case: https://www.kaggle.com/c/titanic/overview
The features we extracted from the data set include ticket category, survival, flight number, age and landing home Dest, room, boat and gender, etc.
Data: http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt

According to the observed data:
- 1. The passenger class refers to the passenger class (1, 2, 3), which is the representative of the socio-economic class.
- 2. The age data is missing.
2 step analysis
- 1. Obtain data
- 2. Basic data processing
- 2.1 determination of characteristic value and target value
- 2.2 missing value handling
- 2.3 data set division
- 3. Feature Engineering (dictionary feature extraction)
- 4. Machine learning (xgboost)
- 5. Model evaluation
3 code implementation
- Import required modules
import pandas as pd import numpy as np from sklearn.feature_extraction import DictVectorizer from sklearn.model_selection import train_test_split
- 1. Obtain data
# 1. Get data
titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")
-
2. Basic data processing
- 2.1 determination of characteristic value and target value
x = titan[["pclass", "age", "sex"]] y = titan["survived"]
- 2.2 missing value handling
# Missing values need to be processed, and these features with categories in the features are extracted from the dictionary features x['age'].fillna(x['age'].mean(), inplace=True)
- 2.3 data set division
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
-
3. Feature Engineering (dictionary feature extraction)
If category symbols appear in the feature, one hot coding processing (DictVectorizer) is required
x.to_dict(orient="records") needs to convert array features into dictionary data
# For converting x to dictionary data x.to_dict(orient="records")
# [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]
transfer = DictVectorizer(sparse=False)
x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.fit_transform(x_test.to_dict(orient="records"))
- 4.xgboost model training and model evaluation
# Model preliminary training from xgboost import XGBClassifier xg = XGBClassifier() xg.fit(x_train, y_train) xg.score(x_test, y_test)
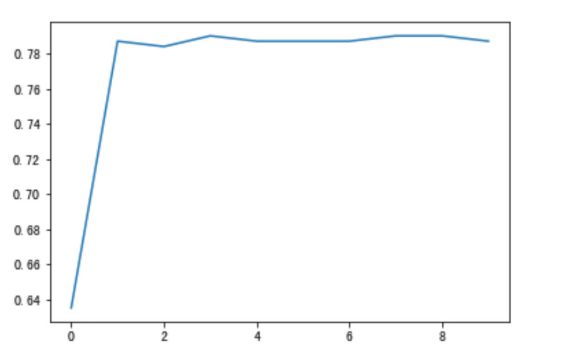
# For max_depth for model tuning
depth_range = range(10)
score = []
for i in depth_range:
xg = XGBClassifier(eta=1, gamma=0, max_depth=i)
xg.fit(x_train, y_train)
s = xg.score(x_test, y_test)
print(s)
score.append(s)
# Result visualization import matplotlib.pyplot as plt plt.plot(depth_range, score) plt.show()
In [1]:
# 1. get data
# 2. Basic data processing
#2.1 determination of characteristic value and target value
#2.2 missing value handling
#2.3 data set division
# 3. Feature Engineering (dictionary feature extraction)
# 4. Machine learning (xgboost)
# 5. Model evaluation
In [2]:
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier, export_graphviz
In [3]:
# 1. get data
titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")
In [4]:
titan
Out[4]:
| row.names | pclass | survived | name | age | embarked | home.dest | room | ticket | boat | sex | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1st | 1 | Allen, Miss Elisabeth Walton | 29.0000 | Southampton | St Louis, MO | B-5 | 24160 L221 | 2 | female |
| 1 | 2 | 1st | 0 | Allison, Miss Helen Loraine | 2.0000 | Southampton | Montreal, PQ / Chesterville, ON | C26 | NaN | NaN | female |
| 2 | 3 | 1st | 0 | Allison, Mr Hudson Joshua Creighton | 30.0000 | Southampton | Montreal, PQ / Chesterville, ON | C26 | NaN | (135) | male |
| 3 | 4 | 1st | 0 | Allison, Mrs Hudson J.C. (Bessie Waldo Daniels) | 25.0000 | Southampton | Montreal, PQ / Chesterville, ON | C26 | NaN | NaN | female |
| 4 | 5 | 1st | 1 | Allison, Master Hudson Trevor | 0.9167 | Southampton | Montreal, PQ / Chesterville, ON | C22 | NaN | 11 | male |
| 5 | 6 | 1st | 1 | Anderson, Mr Harry | 47.0000 | Southampton | New York, NY | E-12 | NaN | 3 | male |
| 6 | 7 | 1st | 1 | Andrews, Miss Kornelia Theodosia | 63.0000 | Southampton | Hudson, NY | D-7 | 13502 L77 | 10 | female |
| 7 | 8 | 1st | 0 | Andrews, Mr Thomas, jr | 39.0000 | Southampton | Belfast, NI | A-36 | NaN | NaN | male |
| 8 | 9 | 1st | 1 | Appleton, Mrs Edward Dale (Charlotte Lamson) | 58.0000 | Southampton | Bayside, Queens, NY | C-101 | NaN | 2 | female |
| 9 | 10 | 1st | 0 | Artagaveytia, Mr Ramon | 71.0000 | Cherbourg | Montevideo, Uruguay | NaN | NaN | (22) | male |
| 10 | 11 | 1st | 0 | Astor, Colonel John Jacob | 47.0000 | Cherbourg | New York, NY | NaN | 17754 L224 10s 6d | (124) | male |
| 11 | 12 | 1st | 1 | Astor, Mrs John Jacob (Madeleine Talmadge Force) | 19.0000 | Cherbourg | New York, NY | NaN | 17754 L224 10s 6d | 4 | female |
| 12 | 13 | 1st | 1 | Aubert, Mrs Leontine Pauline | NaN | Cherbourg | Paris, France | B-35 | 17477 L69 6s | 9 | female |
| 13 | 14 | 1st | 1 | Barkworth, Mr Algernon H. | NaN | Southampton | Hessle, Yorks | A-23 | NaN | B | male |
| 14 | 15 | 1st | 0 | Baumann, Mr John D. | NaN | Southampton | New York, NY | NaN | NaN | NaN | male |
| 15 | 16 | 1st | 1 | Baxter, Mrs James (Helene DeLaudeniere Chaput) | 50.0000 | Cherbourg | Montreal, PQ | B-58/60 | NaN | 6 | female |
| 16 | 17 | 1st | 0 | Baxter, Mr Quigg Edmond | 24.0000 | Cherbourg | Montreal, PQ | B-58/60 | NaN | NaN | male |
| 17 | 18 | 1st | 0 | Beattie, Mr Thomson | 36.0000 | Cherbourg | Winnipeg, MN | C-6 | NaN | NaN | male |
| 18 | 19 | 1st | 1 | Beckwith, Mr Richard Leonard | 37.0000 | Southampton | New York, NY | D-35 | NaN | 5 | male |
| 19 | 20 | 1st | 1 | Beckwith, Mrs Richard Leonard (Sallie Monypeny) | 47.0000 | Southampton | New York, NY | D-35 | NaN | 5 | female |
| 20 | 21 | 1st | 1 | Behr, Mr Karl Howell | 26.0000 | Cherbourg | New York, NY | C-148 | NaN | 5 | male |
| 21 | 22 | 1st | 0 | Birnbaum, Mr Jakob | 25.0000 | Cherbourg | San Francisco, CA | NaN | NaN | (148) | male |
| 22 | 23 | 1st | 1 | Bishop, Mr Dickinson H. | 25.0000 | Cherbourg | Dowagiac, MI | B-49 | NaN | 7 | male |
| 23 | 24 | 1st | 1 | Bishop, Mrs Dickinson H. (Helen Walton) | 19.0000 | Cherbourg | Dowagiac, MI | B-49 | NaN | 7 | female |
| 24 | 25 | 1st | 1 | Bjornstrm-Steffansson, Mr Mauritz Hakan | 28.0000 | Southampton | Stockholm, Sweden / Washington, DC | NaN | D | male | |
| 25 | 26 | 1st | 0 | Blackwell, Mr Stephen Weart | 45.0000 | Southampton | Trenton, NJ | NaN | NaN | (241) | male |
| 26 | 27 | 1st | 1 | Blank, Mr Henry | 39.0000 | Cherbourg | Glen Ridge, NJ | A-31 | NaN | 7 | male |
| 27 | 28 | 1st | 1 | Bonnell, Miss Caroline | 30.0000 | Southampton | Youngstown, OH | C-7 | NaN | 8 | female |
| 28 | 29 | 1st | 1 | Bonnell, Miss Elizabeth | 58.0000 | Southampton | Birkdale, England Cleveland, Ohio | C-103 | NaN | 8 | female |
| 29 | 30 | 1st | 0 | Borebank, Mr John James | NaN | Southampton | London / Winnipeg, MB | D-21/2 | NaN | NaN | male |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 1283 | 1284 | 3rd | 0 | Vestrom, Miss Hulda Amanda Adolfina | NaN | NaN | NaN | NaN | NaN | NaN | female |
| 1284 | 1285 | 3rd | 0 | Vonk, Mr Jenko | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1285 | 1286 | 3rd | 0 | Ware, Mr Frederick | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1286 | 1287 | 3rd | 0 | Warren, Mr Charles William | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1287 | 1288 | 3rd | 0 | Wazli, Mr Yousif | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1288 | 1289 | 3rd | 0 | Webber, Mr James | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1289 | 1290 | 3rd | 1 | Wennerstrom, Mr August Edvard | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1290 | 1291 | 3rd | 0 | Wenzel, Mr Linhart | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1291 | 1292 | 3rd | 0 | Widegren, Mr Charles Peter | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1292 | 1293 | 3rd | 0 | Wiklund, Mr Jacob Alfred | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1293 | 1294 | 3rd | 1 | Wilkes, Mrs Ellen | NaN | NaN | NaN | NaN | NaN | NaN | female |
| 1294 | 1295 | 3rd | 0 | Willer, Mr Aaron | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1295 | 1296 | 3rd | 0 | Willey, Mr Edward | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1296 | 1297 | 3rd | 0 | Williams, Mr Howard Hugh | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1297 | 1298 | 3rd | 0 | Williams, Mr Leslie | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1298 | 1299 | 3rd | 0 | Windelov, Mr Einar | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1299 | 1300 | 3rd | 0 | Wirz, Mr Albert | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1300 | 1301 | 3rd | 0 | Wiseman, Mr Phillippe | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1301 | 1302 | 3rd | 0 | Wittevrongel, Mr Camiel | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1302 | 1303 | 3rd | 1 | Yalsevac, Mr Ivan | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1303 | 1304 | 3rd | 0 | Yasbeck, Mr Antoni | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1304 | 1305 | 3rd | 1 | Yasbeck, Mrs Antoni | NaN | NaN | NaN | NaN | NaN | NaN | female |
| 1305 | 1306 | 3rd | 0 | Youssef, Mr Gerios | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1306 | 1307 | 3rd | 0 | Zabour, Miss Hileni | NaN | NaN | NaN | NaN | NaN | NaN | female |
| 1307 | 1308 | 3rd | 0 | Zabour, Miss Tamini | NaN | NaN | NaN | NaN | NaN | NaN | female |
| 1308 | 1309 | 3rd | 0 | Zakarian, Mr Artun | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1309 | 1310 | 3rd | 0 | Zakarian, Mr Maprieder | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1310 | 1311 | 3rd | 0 | Zenn, Mr Philip | NaN | NaN | NaN | NaN | NaN | NaN | male |
| 1311 | 1312 | 3rd | 0 | Zievens, Rene | NaN | NaN | NaN | NaN | NaN | NaN | female |
| 1312 | 1313 | 3rd | 0 | Zimmerman, Leo | NaN | NaN | NaN | NaN | NaN | NaN | male |
1313 rows × 11 columns
In [5]:
titan.describe()
Out[5]:
| row.names | survived | age | |
|---|---|---|---|
| count | 1313.000000 | 1313.000000 | 633.000000 |
| mean | 657.000000 | 0.341965 | 31.194181 |
| std | 379.174762 | 0.474549 | 14.747525 |
| min | 1.000000 | 0.000000 | 0.166700 |
| 25% | 329.000000 | 0.000000 | 21.000000 |
| 50% | 657.000000 | 0.000000 | 30.000000 |
| 75% | 985.000000 | 1.000000 | 41.000000 |
| max | 1313.000000 | 1.000000 | 71.000000 |
In [6]:
# 2. Basic data processing
#2.1 determination of characteristic value and target value
x = titan[["pclass", "age", "sex"]]
y = titan["survived"]
In [7]:
x.head()
Out[7]:
| pclass | age | sex | |
|---|---|---|---|
| 0 | 1st | 29.0000 | female |
| 1 | 1st | 2.0000 | female |
| 2 | 1st | 30.0000 | male |
| 3 | 1st | 25.0000 | female |
| 4 | 1st | 0.9167 | male |
In [8]:
y.head()
Out[8]:
0 1 1 0 2 0 3 0 4 1 Name: survived, dtype: int64
In [9]:
#2.2 missing value handling
x['age'].fillna(value=titan["age"].mean(), inplace=True)
In [10]:
x.head()
Out[10]:
| pclass | age | sex | |
|---|---|---|---|
| 0 | 1st | 29.0000 | female |
| 1 | 1st | 2.0000 | female |
| 2 | 1st | 30.0000 | male |
| 3 | 1st | 25.0000 | female |
| 4 | 1st | 0.9167 | male |
In [11]:
#2.3 data set division
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22, test_size=0.2)
In [12]:
# 3. Feature Engineering (dictionary feature extraction)
In [13]:
x_train.head()
Out[13]:
| pclass | age | sex | |
|---|---|---|---|
| 649 | 3rd | 45.000000 | female |
| 1078 | 3rd | 31.194181 | male |
| 59 | 1st | 31.194181 | female |
| 201 | 1st | 18.000000 | male |
| 61 | 1st | 31.194181 | female |
In [14]:
x_train = x_train.to_dict(orient="records")
x_test = x_test.to_dict(orient="records")
In [15]:
x_train
Out[15]:
[{'pclass': '3rd', 'age': 45.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 18.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 6.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 27.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 21.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 4.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 13.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 30.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 30.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 50.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 22.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 49.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 62.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 32.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 64.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 23.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 55.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 24.0, 'sex': 'male'},
{'pclass': '1st', 'age': 6.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 10.0, 'sex': 'female'},
{'pclass': '1st', 'age': 53.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 36.0, 'sex': 'female'},
{'pclass': '1st', 'age': 19.0, 'sex': 'male'},
{'pclass': '1st', 'age': 28.0, 'sex': 'male'},
{'pclass': '1st', 'age': 17.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 21.0, 'sex': 'female'},
{'pclass': '1st', 'age': 25.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 19.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '1st', 'age': 21.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 48.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 27.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 46.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 29.0, 'sex': 'female'},
{'pclass': '1st', 'age': 35.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 38.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 32.0, 'sex': 'male'},
{'pclass': '1st', 'age': 16.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 16.0, 'sex': 'male'},
{'pclass': '1st', 'age': 33.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 17.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 36.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 30.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 20.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 33.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 52.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 35.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 25.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 45.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 50.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 52.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 20.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 32.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 34.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 33.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 21.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 45.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 43.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 59.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 47.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 38.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 51.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 36.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 23.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 6.0, 'sex': 'female'},
{'pclass': '1st', 'age': 58.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 4.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 20.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 35.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 12.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 19.0, 'sex': 'male'},
{'pclass': '1st', 'age': 64.0, 'sex': 'male'},
{'pclass': '1st', 'age': 27.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 34.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 18.0, 'sex': 'male'},
{'pclass': '1st', 'age': 48.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 50.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 18.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 34.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 21.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 44.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 19.0, 'sex': 'male'},
{'pclass': '1st', 'age': 39.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 42.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 69.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 2.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 22.0, 'sex': 'male'},
{'pclass': '1st', 'age': 47.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 22.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 42.0, 'sex': 'male'},
{'pclass': '1st', 'age': 21.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 48.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 45.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 45.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 39.0, 'sex': 'male'},
{'pclass': '1st', 'age': 14.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 30.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 32.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 54.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 36.0, 'sex': 'female'},
{'pclass': '1st', 'age': 47.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 0.8333, 'sex': 'male'},
{'pclass': '1st', 'age': 53.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 24.0, 'sex': 'female'},
{'pclass': '1st', 'age': 37.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 25.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 23.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 40.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 23.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 22.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 29.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '1st', 'age': 55.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 26.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 49.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 24.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 22.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 54.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 38.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 42.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 52.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 19.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 8.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 57.0, 'sex': 'male'},
{'pclass': '1st', 'age': 22.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 16.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 45.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 28.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 19.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 28.0, 'sex': 'male'},
{'pclass': '1st', 'age': 24.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 38.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 36.0, 'sex': 'female'},
{'pclass': '1st', 'age': 55.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 25.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 32.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 9.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '1st', 'age': 29.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 40.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 39.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 25.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 49.0, 'sex': 'male'},
{'pclass': '1st', 'age': 36.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 23.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 23.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 17.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 24.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 28.0, 'sex': 'male'},
{'pclass': '1st', 'age': 40.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 6.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 17.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 34.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 41.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 28.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 61.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 17.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 3.0, 'sex': 'male'},
{'pclass': '1st', 'age': 24.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 30.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 41.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 42.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 28.0, 'sex': 'male'},
{'pclass': '1st', 'age': 48.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 50.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 16.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 40.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 23.0, 'sex': 'female'},
{'pclass': '1st', 'age': 34.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 39.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 34.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 22.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 9.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 22.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 30.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 25.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 24.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 26.0, 'sex': 'female'},
{'pclass': '1st', 'age': 57.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 39.0, 'sex': 'male'},
{'pclass': '1st', 'age': 35.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 41.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 67.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 11.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 22.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 20.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 50.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 33.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 36.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 48.0, 'sex': 'female'},
{'pclass': '1st', 'age': 59.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 25.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 17.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 45.0, 'sex': 'female'},
{'pclass': '1st', 'age': 49.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 33.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 46.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 52.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 36.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 28.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 28.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 19.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 43.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 36.0, 'sex': 'male'},
{'pclass': '1st', 'age': 51.0, 'sex': 'male'},
{'pclass': '1st', 'age': 36.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 3.0, 'sex': 'male'},
{'pclass': '1st', 'age': 48.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 48.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 16.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 36.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 44.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 36.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 37.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 32.0, 'sex': 'male'},
{'pclass': '1st', 'age': 30.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 22.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 40.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 24.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 65.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 37.0, 'sex': 'female'},
{'pclass': '1st', 'age': 52.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 23.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 0.8333, 'sex': 'male'},
{'pclass': '2nd', 'age': 35.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 27.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 27.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 41.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 18.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 33.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 56.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 40.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 9.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 28.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 30.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 25.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 48.0, 'sex': 'female'},
{'pclass': '1st', 'age': 36.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 35.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 1.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 2.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 32.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 25.0, 'sex': 'male'},
{'pclass': '1st', 'age': 29.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 21.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 27.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 38.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 28.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 0.9167, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 39.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 9.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 45.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 20.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 36.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 14.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 30.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 22.0, 'sex': 'male'},
{'pclass': '1st', 'age': 60.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 20.0, 'sex': 'male'},
{'pclass': '1st', 'age': 48.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 28.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 23.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 32.0, 'sex': 'male'},
{'pclass': '1st', 'age': 30.0, 'sex': 'male'},
{'pclass': '1st', 'age': 46.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 32.0, 'sex': 'male'},
{'pclass': '1st', 'age': 27.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 61.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 39.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 0.1667, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 15.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 24.0, 'sex': 'male'},
{'pclass': '1st', 'age': 17.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 42.0, 'sex': 'female'},
{'pclass': '1st', 'age': 20.0, 'sex': 'female'},
{'pclass': '1st', 'age': 62.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 49.0, 'sex': 'male'},
{'pclass': '1st', 'age': 23.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 33.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 19.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 45.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 70.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 37.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 28.0, 'sex': 'male'},
{'pclass': '1st', 'age': 54.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 51.0, 'sex': 'female'},
{'pclass': '1st', 'age': 21.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 64.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 29.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 33.0, 'sex': 'male'},
{'pclass': '1st', 'age': 50.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 19.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 59.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 49.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 38.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 48.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 54.0, 'sex': 'female'},
{'pclass': '1st', 'age': 19.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 3.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 18.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 22.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 34.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 28.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 15.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 40.0, 'sex': 'female'},
{'pclass': '1st', 'age': 46.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 8.0, 'sex': 'female'},
{'pclass': '1st', 'age': 63.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 43.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 16.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 38.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 1.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 35.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.0, 'sex': 'male'},
{'pclass': '1st', 'age': 42.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 38.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 17.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 40.0, 'sex': 'male'},
{'pclass': '1st', 'age': 4.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 29.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 22.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 57.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 40.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 47.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 37.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 42.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 21.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 5.0, 'sex': 'female'},
{'pclass': '1st', 'age': 21.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 40.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 9.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 41.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 36.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 28.0, 'sex': 'male'},
{'pclass': '1st', 'age': 39.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 35.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 24.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 45.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 24.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 50.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 56.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 32.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 19.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 45.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 22.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 50.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 30.0, 'sex': 'male'},
{'pclass': '1st', 'age': 24.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 40.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 21.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 52.0, 'sex': 'male'},
{'pclass': '1st', 'age': 45.0, 'sex': 'male'},
{'pclass': '1st', 'age': 11.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 23.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 26.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 40.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 49.0, 'sex': 'male'},
{'pclass': '1st', 'age': 18.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 9.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 25.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 35.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 32.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 21.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 32.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 45.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 26.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 21.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 25.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'male'},
{'pclass': '1st', 'age': 36.0, 'sex': 'male'},
{'pclass': '1st', 'age': 27.0, 'sex': 'male'},
{'pclass': '1st', 'age': 24.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 18.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 56.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 16.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 18.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 64.0, 'sex': 'male'},
{'pclass': '1st', 'age': 46.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 18.0, 'sex': 'male'},
{'pclass': '1st', 'age': 46.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 29.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 18.0, 'sex': 'female'},
{'pclass': '1st', 'age': 33.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 34.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 0.8333, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 58.0, 'sex': 'female'},
{'pclass': '1st', 'age': 60.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 23.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 44.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 71.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 13.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 58.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 4.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 16.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 33.0, 'sex': 'female'},
{'pclass': '1st', 'age': 33.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 48.0, 'sex': 'male'},
{'pclass': '1st', 'age': 28.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 55.0, 'sex': 'female'},
{'pclass': '1st', 'age': 54.0, 'sex': 'male'},
{'pclass': '1st', 'age': 71.0, 'sex': 'male'},
{'pclass': '1st', 'age': 47.0, 'sex': 'female'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 21.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 21.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 24.0, 'sex': 'male'},
{'pclass': '1st', 'age': 23.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 18.0, 'sex': 'female'},
{'pclass': '1st', 'age': 54.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 17.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 6.0, 'sex': 'male'},
{'pclass': '1st', 'age': 45.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 36.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 55.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 26.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '1st', 'age': 65.0, 'sex': 'male'},
{'pclass': '1st', 'age': 27.0, 'sex': 'male'},
{'pclass': '1st', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 22.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '2nd', 'age': 7.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 30.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 39.0, 'sex': 'female'},
{'pclass': '1st', 'age': 19.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 19.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 20.0, 'sex': 'male'},
{'pclass': '1st', 'age': 56.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 38.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 23.0, 'sex': 'female'},
{'pclass': '2nd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 42.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 23.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 25.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '2nd', 'age': 16.0, 'sex': 'male'},
{'pclass': '2nd', 'age': 42.0, 'sex': 'male'},
{'pclass': '3rd', 'age': 2.0, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'female'},
{'pclass': '3rd', 'age': 31.19418104265403, 'sex': 'male'},
{'pclass': '1st', 'age': 36.0, 'sex': 'male'},
...]In [16]:
transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
In [21]:
# 4.xgboost model training
#4.1 preliminary model training
from xgboost import XGBClassifier
xg = XGBClassifier()
xg.fit(x_train, y_train)
Out[21]:
XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=1, gamma=0,
learning_rate=0.1, max_delta_step=0, max_depth=3,
min_child_weight=1, missing=None, n_estimators=100, n_jobs=1,
nthread=None, objective='binary:logistic', random_state=0,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=None, subsample=1, verbosity=1)In [22]:
xg.score(x_test, y_test)
Out[22]:
0.7832699619771863
In [23]:
#4.2 max_depth for tuning
depth_range = range(10)
score = []
for i in depth_range:
xg = XGBClassifier(eta=1, gamma=0, max_depth=i)
xg.fit(x_train, y_train)
s = xg.score(x_test, y_test)
print(s)
score.append(s)
0.6311787072243346 0.7908745247148289 0.7870722433460076 0.7832699619771863 0.7870722433460076 0.7908745247148289 0.7908745247148289 0.7946768060836502 0.7908745247148289 0.7946768060836502
In [25]:
#4.3 visualization of tuning results
import matplotlib.pyplot as plt
plt.plot(depth_range, score)
plt.show()
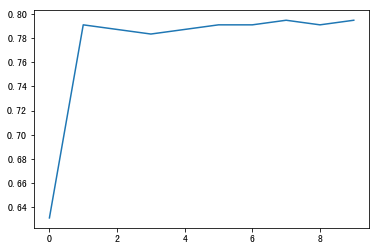
5.4 otto case introduction -- Otto Group Product Classification Challenge [xgboost implementation]
1 background introduction
Otto group is one of the largest e-commerce companies in the world, with subsidiaries in more than 20 countries. The company sells millions of products around the world every day, so it is very important to classify its products according to their performance.
However, in practice, the staff found that many of the same products have been classified differently. This case requires you to correctly classify the products of Alto group. Provide classification accuracy as much as possible.
Link: https://www.kaggle.com/c/otto-group-product-classification-challenge/overview
2 thinking analysis
-
1. Data acquisition
-
2. Basic data processing
- 2.1 intercepting some data
- 2.2 converting label paper into numbers
- 2.3 split data (using structured shufflesplit)
- 2.4 data standardization
- 2.5 data pca dimensionality reduction
-
3. Model training
- 3.1 basic model training
- 3.2 model tuning
- 3.2. 1. Tuning parameters:
- n_estimator,
- max_depth,
- min_child_weights,
- subsamples,
- consample_bytrees,
- etas
- 3.2. 2 determine the final optimal parameters
- 3.2. 1. Tuning parameters:
Part 3 code implementation
-
2. Basic data processing
-
2.1 intercepting some data
-
2.2 converting label paper into numbers
-
2.3 split data (using structured shufflesplit)
# Use structured shufflesplit to split the dataset from sklearn.model_selection import StratifiedShuffleSplit sss = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=0) for train_index, test_index in sss.split(X_resampled.values, y_resampled): print(len(train_index)) print(len(test_index)) x_train = X_resampled.values[train_index] x_val = X_resampled.values[test_index] y_train = y_resampled[train_index] y_val = y_resampled[test_index]# Graphical visualization of segmented data import seaborn as sns sns.countplot(y_val) plt.show()
-
2.4 data standardization
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(x_train) x_train_scaled = scaler.transform(x_train) x_val_scaled = scaler.transform(x_val)
-
2.5 data pca dimensionality reduction
print(x_train_scaled.shape) # (13888, 93) from sklearn.decomposition import PCA pca = PCA(n_components=0.9) x_train_pca = pca.fit_transform(x_train_scaled) x_val_pca = pca.transform(x_val_scaled) print(x_train_pca.shape, x_val_pca.shape) (13888, 65) (3473, 65)
From the data output above, it can be seen that only 65 elements can express 90% of the information in the feature
# Dimensionality reduction data visualization plt.plot(np.cumsum(pca.explained_variance_ratio_)) plt.xlabel("Number of elements") plt.ylabel("Percentage of expressible information") plt.show()
-
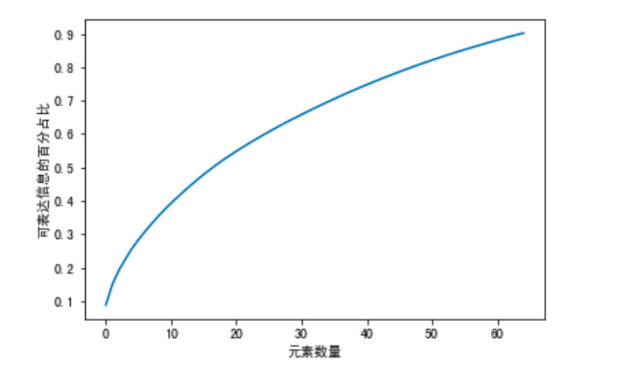
-
3. Model training
-
3.1 basic model training
from xgboost import XGBClassifier xgb = XGBClassifier() xgb.fit(x_train_pca, y_train) # Change the output mode of the predicted value so that the output result is the percentage and reduce the logloss value y_pre_proba = xgb.predict_proba(x_val_pca)
# logloss for model evaluation from sklearn.metrics import log_loss log_loss(y_val, y_pre_proba, eps=1e-15, normalize=True) xgb.get_params
-
-
3.2 model tuning
-
3.2. 1. Tuning parameters:
-
n_estimator,
scores_ne = [] n_estimators = [100,200,400,450,500,550,600,700] for nes in n_estimators: print("n_estimators:", nes) xgb = XGBClassifier(max_depth=3, learning_rate=0.1, n_estimators=nes, objective="multi:softprob", n_jobs=-1, nthread=4, min_child_weight=1, subsample=1, colsample_bytree=1, seed=42) xgb.fit(x_train_pca, y_train) y_pre = xgb.predict_proba(x_val_pca) score = log_loss(y_val, y_pre) scores_ne.append(score) print("Of test data logloss Value is:{}".format(score))# Data change visualization plt.plot(n_estimators, scores_ne, "o-") plt.ylabel("log_loss") plt.xlabel("n_estimators") print("n_estimators The optimal value is:{}".format(n_estimators[np.argmin(scores_ne)]))
-
-
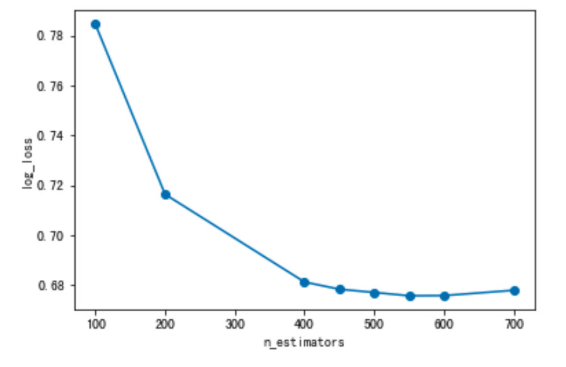
-
-
-
max_depth,
scores_md = [] max_depths = [1,3,5,6,7] for md in max_depths: # modify xgb = XGBClassifier(max_depth=md, # modify learning_rate=0.1, n_estimators=n_estimators[np.argmin(scores_ne)], # modify objective="multi:softprob", n_jobs=-1, nthread=4, min_child_weight=1, subsample=1, colsample_bytree=1, seed=42) xgb.fit(x_train_pca, y_train) y_pre = xgb.predict_proba(x_val_pca) score = log_loss(y_val, y_pre) scores_md.append(score) # modify print("Of test data logloss Value is:{}".format(log_loss(y_val, y_pre)))# Data change visualization plt.plot(max_depths, scores_md, "o-") # modify plt.ylabel("log_loss") plt.xlabel("max_depths") # modify print("max_depths The optimal value is:{}".format(max_depths[np.argmin(scores_md)])) # modify -
min_child_weights,
- Adjust according to the above mode
-
subsamples,
-
consample_bytrees,
-
etas
-
-
3.2. 2 determine the final optimal parameters
xgb = XGBClassifier(learning_rate =0.1, n_estimators=550, max_depth=3, min_child_weight=3, subsample=0.7, colsample_bytree=0.7, nthread=4, seed=42, objective='multi:softprob') xgb.fit(x_train_scaled, y_train) y_pre = xgb.predict_proba(x_val_scaled) print("Of test data logloss Value is : {}".format(log_loss(y_val, y_pre, eps=1e-15, normalize=True)))
-
In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
Data acquisition
In [2]:
data = pd.read_csv("./data/otto/train.csv")
In [3]:
data.head()
Out[3]:
| id | feat_1 | feat_2 | feat_3 | feat_4 | feat_5 | feat_6 | feat_7 | feat_8 | feat_9 | ... | feat_85 | feat_86 | feat_87 | feat_88 | feat_89 | feat_90 | feat_91 | feat_92 | feat_93 | target | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Class_1 |
| 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Class_1 |
| 2 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Class_1 |
| 3 | 4 | 1 | 0 | 0 | 1 | 6 | 1 | 5 | 0 | 0 | ... | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | Class_1 |
| 4 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | Class_1 |
5 rows × 95 columns
In [4]:
data.shape
Out[4]:
(61878, 95)
In [5]:
data.describe()
Out[5]:
| id | feat_1 | feat_2 | feat_3 | feat_4 | feat_5 | feat_6 | feat_7 | feat_8 | feat_9 | ... | feat_84 | feat_85 | feat_86 | feat_87 | feat_88 | feat_89 | feat_90 | feat_91 | feat_92 | feat_93 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 61878.000000 | 61878.00000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | ... | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 | 61878.000000 |
| mean | 30939.500000 | 0.38668 | 0.263066 | 0.901467 | 0.779081 | 0.071043 | 0.025696 | 0.193704 | 0.662433 | 1.011296 | ... | 0.070752 | 0.532306 | 1.128576 | 0.393549 | 0.874915 | 0.457772 | 0.812421 | 0.264941 | 0.380119 | 0.126135 |
| std | 17862.784315 | 1.52533 | 1.252073 | 2.934818 | 2.788005 | 0.438902 | 0.215333 | 1.030102 | 2.255770 | 3.474822 | ... | 1.151460 | 1.900438 | 2.681554 | 1.575455 | 2.115466 | 1.527385 | 4.597804 | 2.045646 | 0.982385 | 1.201720 |
| min | 1.000000 | 0.00000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 15470.250000 | 0.00000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 50% | 30939.500000 | 0.00000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 75% | 46408.750000 | 0.00000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| max | 61878.000000 | 61.00000 | 51.000000 | 64.000000 | 70.000000 | 19.000000 | 10.000000 | 38.000000 | 76.000000 | 43.000000 | ... | 76.000000 | 55.000000 | 65.000000 | 67.000000 | 30.000000 | 61.000000 | 130.000000 | 52.000000 | 19.000000 | 87.000000 |
8 rows × 94 columns
In [6]:
#Graphical visualization, viewing data distribution
import seaborn as sns
sns.countplot(data.target)
plt.show()
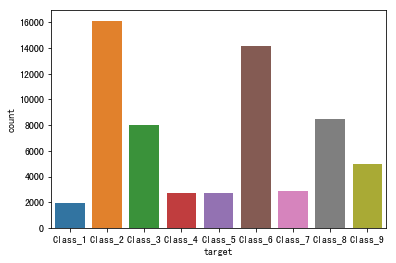
As can be seen from the above figure, the data category is unbalanced, so post-processing is required
Basic data processing
The data has been desensitized and no special processing is required
Intercept some data
In [7]:
new1_data = data[:10000]
new1_data.shape
Out[7]:
(10000, 95)
In [8]:
#Graphical visualization, viewing data distribution
import seaborn as sns
sns.countplot(new1_data.target)
plt.show()
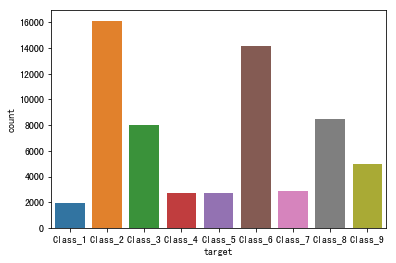
It is not feasible to obtain the data in the above way, and then use random undersampling to obtain the data of the response
In [9]:
#Random undersampling data acquisition
#First, you need to determine the characteristic value \ label value
y = data["target"]
x = data.drop(["id", "target"], axis=1)
In [10]:
x.head()
Out[10]:
| feat_1 | feat_2 | feat_3 | feat_4 | feat_5 | feat_6 | feat_7 | feat_8 | feat_9 | feat_10 | ... | feat_84 | feat_85 | feat_86 | feat_87 | feat_88 | feat_89 | feat_90 | feat_91 | feat_92 | feat_93 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 1 | 6 | 1 | 5 | 0 | 0 | 1 | ... | 22 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
5 rows × 93 columns
In [11]:
y.head()
Out[11]:
0 Class_1 1 Class_1 2 Class_1 3 Class_1 4 Class_1 Name: target, dtype: object
In [12]:
#Under sampling data acquisition
from imblearn.under_sampling import RandomUnderSampler
rus = RandomUnderSampler(random_state=0)
X_resampled, y_resampled = rus.fit_resample(x, y)
In [13]:
x.shape, y.shape
Out[13]:
((61878, 93), (61878,))
In [14]:
X_resampled.shape, y_resampled.shape
Out[14]:
((17361, 93), (17361,))
In [15]:
#Graphical visualization, viewing data distribution
import seaborn as sns
sns.countplot(y_resampled)
plt.show()
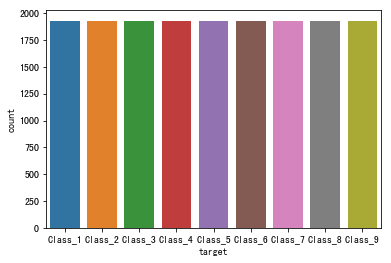
Convert tag values to numbers
In [16]:
y_resampled.head()
Out[16]:
0 Class_1 1 Class_1 2 Class_1 3 Class_1 4 Class_1 Name: target, dtype: object
In [17]:
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y_resampled = le.fit_transform(y_resampled)
In [18]:
y_resampled
Out[18]:
array([0, 0, 0, ..., 8, 8, 8])
Split data
In [19]:
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X_resampled, y_resampled, test_size=0.2)
In [20]:
x_train.shape, y_train.shape
Out[20]:
((13888, 93), (13888,))
In [21]:
x_test.shape, y_test.shape
Out[21]:
((3473, 93), (3473,))
In [22]:
# 1. Data acquisition
# 2. Basic data processing
# 2.1 intercepting partial data
# 2.2 converting label paper into numbers
# 2.3 split data (using structured shufflesplit)
# 2.4 data standardization
# 2.5 data pca dimensionality reduction
# 3. model training
# 3.1 basic model training
# 3.2 model tuning
# 3.2. 1. Tuning parameters:
# n_estimator,
# max_depth,
# min_child_weights,
# subsamples,
# consample_bytrees,
# etas
# 3.2. 2 determine the final optimal parameters
In [23]:
#Graphic visualization
import seaborn as sns
sns.countplot(y_test)
plt.show()
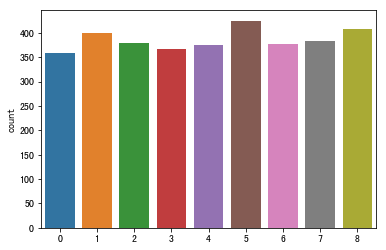
In [28]:
#Data segmentation through structured shufflesplit
from sklearn.model_selection import StratifiedShuffleSplit
sss = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=0)
for train_index, test_index in sss.split(X_resampled.values, y_resampled):
print(len(train_index))
print(len(test_index))
x_train = X_resampled.values[train_index]
x_val = X_resampled.values[test_index]
y_train = y_resampled[train_index]
y_val = y_resampled[test_index]
13888 3473
In [29]:
print(x_train.shape, x_val.shape)
(13888, 93) (3473, 93)
In [30]:
#Graphic visualization
import seaborn as sns
sns.countplot(y_val)
plt.show()
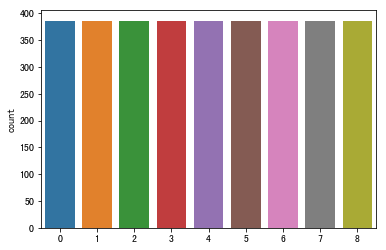
Data standardization
In [31]:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(x_train)
x_train_scaled = scaler.transform(x_train)
x_val_scaled = scaler.transform(x_val)
Data PCA dimensionality reduction
In [33]:
x_train_scaled.shape
Out[33]:
(13888, 93)
In [34]:
from sklearn.decomposition import PCA
pca = PCA(n_components=0.9)
x_train_pca = pca.fit_transform(x_train_scaled)
x_val_pca = pca.transform(x_val_scaled)
In [35]:
print(x_train_pca.shape, x_val_pca.shape)
(13888, 65) (3473, 65)
In [37]:
#Visual data dimensionality reduction information change degree
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel("number of elements")
plt.ylabel("percentage of expressed information")
plt.show()
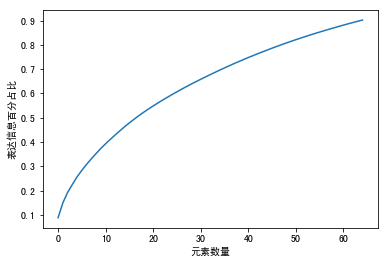
model training
Basic model training
In [38]:
from xgboost import XGBClassifier
xgb = XGBClassifier()
xgb.fit(x_train_pca, y_train)
Out[38]:
XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=1, gamma=0,
learning_rate=0.1, max_delta_step=0, max_depth=3,
min_child_weight=1, missing=None, n_estimators=100, n_jobs=1,
nthread=None, objective='multi:softprob', random_state=0,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=None, subsample=1, verbosity=1)In [39]:
#Output the predicted value, and the predicted value with percentage proportion must be output
y_pre_proba = xgb.predict_proba(x_val_pca)
In [40]:
y_pre_proba
Out[40]:
array([[0.4893983 , 0.00375719, 0.00225278, ..., 0.06179977, 0.17131925,
0.03980364],
[0.14336601, 0.01110009, 0.01018962, ..., 0.00691424, 0.02062171,
0.7525783 ],
[0.00834821, 0.14602502, 0.65013766, ..., 0.01385602, 0.00602207,
0.00240582],
...,
[0.09568001, 0.00293341, 0.00582061, ..., 0.1031019 , 0.7587154 ,
0.02730099],
[0.40236628, 0.12317444, 0.03567632, ..., 0.18818544, 0.13276173,
0.07105519],
[0.00473167, 0.01536749, 0.02546864, ..., 0.00882399, 0.88531935,
0.00384397]], dtype=float32)In [42]:
#logloss assessment
from sklearn.metrics import log_loss
log_loss(y_val, y_pre_proba, eps=1e-15, normalize=True)
Out[42]:
0.7845457684689274
In [43]:
xgb.get_params
Out[43]:
<bound method XGBModel.get_params of XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=1, gamma=0,
learning_rate=0.1, max_delta_step=0, max_depth=3,
min_child_weight=1, missing=None, n_estimators=100, n_jobs=1,
nthread=None, objective='multi:softprob', random_state=0,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=None, subsample=1, verbosity=1)>Model tuning
Determine the optimal estimators
In [44]:
scores_ne = []
n_estimators = [100, 200, 300, 400, 500, 550, 600, 700]
In [49]:
for nes in n_estimators:
print("n_estimators:", nes)
xgb = XGBClassifier(max_depth=3,
learning_rate=0.1,
n_estimators=nes,
objective="multi:softprob",
n_jobs=-1,
nthread=4,
min_child_weight=1,
subsample=1,
colsample_bytree=1,
seed=42)
xgb.fit(x_train_pca, y_train)
y_pre = xgb.predict_proba(x_val_pca)
score = log_loss(y_val, y_pre)
scores_ne.append(score)
print("the logloss value of each test is: {}". format(score))
n_estimators: 100 Of each test logloss Value is:0.7845457684689274 n_estimators: 200 Of each test logloss Value is:0.7163659085830947 n_estimators: 300 Of each test logloss Value is:0.6933389946023942 n_estimators: 400 Of each test logloss Value is:0.68119252278615 n_estimators: 500 Of each test logloss Value is:0.67700775120196 n_estimators: 550 Of each test logloss Value is:0.6756911007299885 n_estimators: 600 Of each test logloss Value is:0.6757532660164814 n_estimators: 700 Of each test logloss Value is:0.6778721089881976
In [50]:
#Graphically display the corresponding logloss value
plt.plot(n_estimators, scores_ne, "o-")
plt.xlabel("n_estimators")
plt.ylabel("log_loss")
plt.show()
print("the optimal n_estimators value is: {}". format(n_estimators[np.argmin(scores_ne)]))
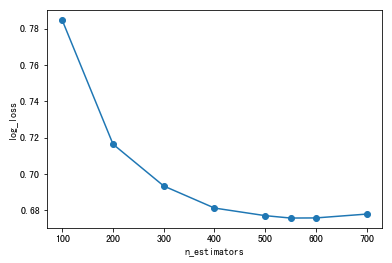
Optimal n_estimators Value is:550
Determine the optimal max_depth
In [63]:
scores_md = []
max_depths = [1,3,5,6,7]
In [64]:
for md in max_depths:
print("max_depth:", md)
xgb = XGBClassifier(max_depth=md,
learning_rate=0.1,
n_estimators=n_estimators[np.argmin(scores_ne)],
objective="multi:softprob",
n_jobs=-1,
nthread=4,
min_child_weight=1,
subsample=1,
colsample_bytree=1,
seed=42)
xgb.fit(x_train_pca, y_train)
y_pre = xgb.predict_proba(x_val_pca)
score = log_loss(y_val, y_pre)
scores_md.append(score)
print("the logloss value of each test is: {}". format(score))
max_depth: 1 Of each test logloss Value is:0.8186777106711784 max_depth: 3 Of each test logloss Value is:0.6756911007299885 max_depth: 5 Of each test logloss Value is:0.730323661087053 max_depth: 6 Of each test logloss Value is:0.7693314501840949 max_depth: 7 Of each test logloss Value is:0.7889236364892144
In [67]:
#Graphically display the corresponding logloss value
plt.plot(max_depths, scores_md, "o-")
plt.xlabel("max_depths")
plt.ylabel("log_loss")
plt.show()
print("the optimal max_depths value is: {}". format(max_depths[np.argmin(scores_md)]))
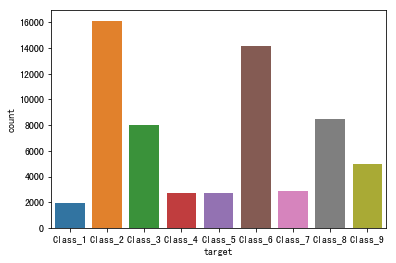
Optimal max_depths Value is:3
Run and debug the following parameters according to the above mode
min_child_weights,
subsamples,
consample_bytrees,
etas
In [69]:
xgb = XGBClassifier(learning_rate =0.1,
n_estimators=550,
max_depth=3,
min_child_weight=3,
subsample=0.7,
colsample_bytree=0.7,
nthread=4,
seed=42,
objective='multi:softprob')
xgb.fit(x_train_scaled, y_train)
y_pre = xgb.predict_proba(x_val_scaled)
print("the log_loss value of the test data is: {}". format(log_loss(y_val, y_pre, eps=1e-15, normalize=True)))
Of test data log_loss Value is : 0.5944022517380477