genetic algorithm

Genetic algorithm is an iterative optimization algorithm that simulates the evolution mechanism of natural organisms. By simulating the law of "survival of the fittest, survival of the fittest", it finds the most suitable solution among all possible solutions

1. Basic principles

In genetic algorithm, after the initial population is formed by coding, the task of genetic operation is to realize the evolution process of "survival of the fittest" by evaluating the fitness of each individual in the population and then screening. From the perspective of optimization search, genetic operation can optimize the solution of the problem generation by generation, so as to approach the optimal solution

Genetic algorithm consists of three basic genetic operators: selection, crossover and mutation

It should be noted that although the operation of individual genetic operators is carried out under the condition of random disturbance, there is a difference between this kind of random operation and the traditional random search method: genetic operation is an efficient and directed search

The effect of genetic operation is closely related to the operation probability, coding method, population size, initial population and fitness function

1.1 choice

We call the operation of "selecting the superior individual from the group and eliminating the inferior individual" selection. The selection operator is also called the regeneration operator

The selection operation is based on the fitness evaluation of the individuals in the group

Roulette selection is the simplest and most commonly used method. In this method, the probability of each individual's selection is in direct proportion to its fitness value:

I f the population size is n n n, and the fitness of individual I I I is FIF {I} fi, then the probability of iii being selected is Pi=fi ∑ I = 1nfi. P {I} = \ frac {f {I}} {\ sum {I = 1} ^ {n} f {I}}}. Pi = ∑ i=1n fi

After calculating the selection probability of each individual in the group, in order to select "mating" individuals, multiple rounds of selection are needed. In each round of selection, a uniform random number between 0, 10, 10 and 1 will be generated, and it will be used as a pointer to determine the selected individual. After the individual is selected, the cross pairing can be formed randomly for subsequent cross operations

1.2 crossover

In the process of biological evolution in nature, recombination (including mutation) of biological genetic factors plays a key role. Correspondingly, crossover operator of genetic operation plays a key role in genetic algorithm. Crossover refers to the operation of replacing and recombining part of the structure of two parent individuals to generate new individuals

Crossover operators randomly exchange some "genes" between two individuals in the population according to the crossover rate, according to the difference of "gene" coding representation. There are discrete recombination, intermediate recombination, linear recombination, extended linear recombination, single point / multi-point crossover, uniform crossover, shuffle crossover, reduced proxy crossover and other operators. The most commonly used crossover operator is single point crossover. Its specific operation is: random in the individual string When a crossing point is set, the partial structure of two individuals before or after the point is exchanged, and two new individuals are generated

1.3 variation

The mutation operator changes the "gene value" of some "loci" on the individual string in a population. According to the different representation methods of individual coding, there are the following algorithms: real value mutation and binary mutation

In general, the basic operation steps of mutation operator are as follows:

1. All the individuals in the group are judged to be mutated by the preset mutation probability
2. The individuals who are determined to be mutated are randomly selected to mutate

The purpose of introducing the concept and function of "mutation" into genetic algorithm is as follows:

1. The genetic algorithm has the ability of local random search. When the genetic algorithm approaches the neighborhood of the optimal solution through crossover operator, the local random search ability of mutation operator can accelerate the convergence to the optimal solution
2. The genetic algorithm can maintain population diversity and avoid premature convergence

In the genetic algorithm, the crossover operator is the main operator because of its strong global search ability, and the mutation operator is the auxiliary operator because of its outstanding local search ability. Through the combination of these two operators, the genetic algorithm can give consideration to the uniform search ability of global search and local search

When a population is trapped in a hyperplane of search space in evolution, and can't get rid of it only by crossing, the hyperplane can be got rid of by mutation operation

When the expected "algorithm block" has been formed by crossover operator, mutation operation may destroy it

1.4 termination conditions

When the fitness of the optimal individual reaches the set threshold, or the fitness and group fitness of the optimal individual no longer rise, or the number of iterations reaches the threshold, the algorithm terminates. The preset number of iterations is generally 100 − 500100-500100 − 500 generations

2. Program design

This section explains the program design of genetic algorithm and MATLAB Toolbox:

The adaptive values of individuals in P(t)P(t)P(t) P (T) P(t)P(t)P(t) P (T) P(t)P(t)P(t) P (T) P(t)P(t)P(t) P (T) P(t)P(t)P(t) P (T) P (T) were calculated

Begin
t = 0
initialize P(t)
calculate the fitness value of P(t)
while(Not satisfied with the stopping critiria)
    do
    begin
    t += 1
    choose P(t) from P(t+1)
    reassemble P(t)
    calculate the fitness value of P(t)
end

[case]

Seeking function:
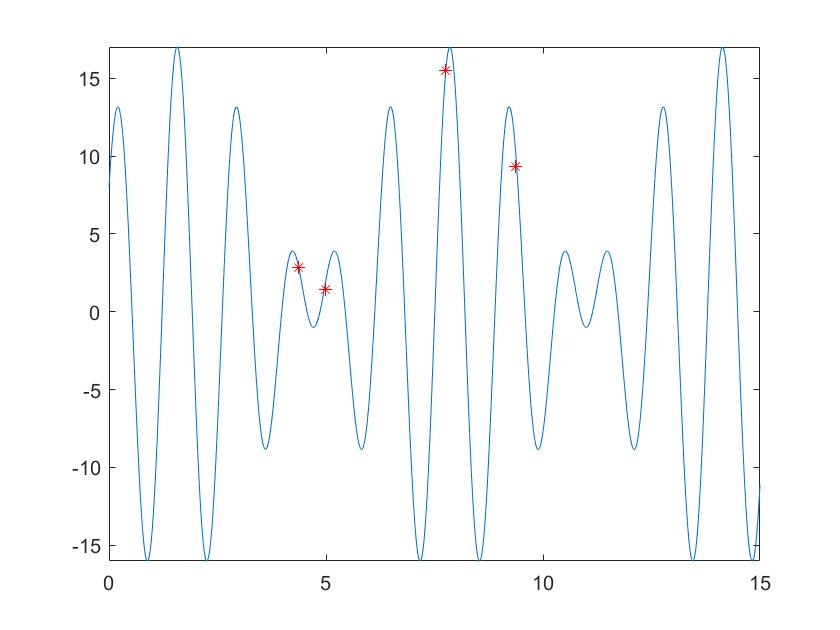
f(x)=9sin(5x)+8cos(4x),    x∈[0,15]f(x) = 9sin(5x) + 8cos(4x),\ \ \ \ x \in [0,15]f(x)=9sin(5x)+8cos(4x),    x∈[0,15]
The maximum value of

[solution]

1. initpop.m

   initpop.m is used to initialize the population. popsize represents the population size, and chromlength represents the chromosome length. It depends on the binary encoding length of the variable

%Initialization
function pop = initpop(popsize, chromlength)
pop = round(rand(popsize, chromlength));
%rand The function randomly generates each element as {0,1} ,The number of rows is popsize ,The number of columns is chromlength Matrix
%round Function to round every element in a matrix, So we have a random initial population
end

1. decodechrom.m

   Binary to decimal: the function of decodechrom.m is to convert chromosomes (binary encoding) to decimal

function pop2 = decodebinary(pop)
[px,py] = size(pop);    %seek pop Row,Column number
for i = 1:py
    pop1(:,i) = 2.^(py-i).*pop(:,i);
end
pop2 = sum(pop1,2);     %seek pop1 Elements and
end

%Intercept code length
function pop2 = decodechrom(pop,spoint,length)
pop1 = pop(:,spoint:spoint+length-1);
pop2 = decodebinary(pop1);
end

1. calobjvalue.m
   The function is to calculate the objective function

function[objvalue] = calobjvalue(pop)
temp1 = decodechrom(pop,1,10);
x = temp1*10/1023;
objvalue = 10*sin(5*x)+7*cos(4*x);
end

1. calfitvalue.m
   The function is to calculate the fitness value of an individual

function fitvalue = calfitvalue(objvalue)
global Cmin;
Cmin = 0;
[px,py] = size(objvalue);
for i = 1:px
    if objvalue(i) + Cmin>0
        temp = Cmin + objvalue(i);
    else
        temp = 0.0;
    end
    fitvalue(i) = temp;
end
fitvalue = fitvalue'

1. selection.m
   The function function is to select replication. Selecting replication will determine which individuals can enter the next generation. The program uses roulette selection method to select individuals:

function [newpop] = selection(pop,fitvalue)
totalfit = sum(fitvalue);       %Calculate the sum of fitness values
fitvalue = fitvalue/totalfit;   %Calculate the probability of individual selection
fitvalue = cumsum(fitvalue);
[px,py] = size(pop);
ms = sort(rand(px,1));          %Arrange from small to large
fitin = 1;
newin = 1;
while newin <= px
    if(ms(newin))<fitvalue(fitin)
        newpop(newin) = pop(fitin);
        newin = newin + 1;
    else
        fitin = fitin + 1;
    end
end

1. crossover.m
   The function is to make every individual in the group cross with probability pc

function [newpop] = crossover(pop,pc)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:2:px-1
    if(rand<pc)
        cpoint = round(rand*py);
        newpop(i,:) = [pop(i,1:cpoint),pop(i+1,cpoint+1:py)];
        newpop(i+1,:) = [pop(i+1,1:cpoint),pop(i,cpoint+1:py)];
    else
        newpop(i,:) = pop(i);
        newpop(i+1,:) = pop(i+1);
    end
end

1. mutation.m
   The function is to realize mutation: every bit of every individual in the parent generation is flipped randomly with probability pm

function [newpop] = mutation(pop,pm)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
    if (rand<pm)
        mpoint = round(rand*py);
        if mpoint <=0
            mpoint = 1;
        end
        newpop(i) = pop(i);
        if any(newpop(i,mpoint)) == 0
            newpop(i,mpoint) = 1;
        else
            newpop(i,mpoint) = 0;
        end
    else
        newpop(i) = pop(i);
    end
end

1. best.m
   The function is to find out the maximum fitness and the most suitable individual

function [bestindividual,bestfit] = best(pop,fitvalue)
[px,py] = size(pop);
bestindividual = pop(1,:);
bestfit = fitvalue(1);
for i=2:px
    if fitvalue(i)>bestfit
        bestindividual = pop(i,:);
        bestfit = fitvalue(i);
    end
end

1. main.m
   Main program:

clc;clear all;
popsize = 20;       %Group size
chromlength = 10;   %String length
pc = 0.7;           %Crossover probability
pm = 0.005;           %Mutation probability
pop = initpop(popsize, chromlength);
for i = 1:20
    [objvalue] = calobjvalue(pop);
    fitvalue = calfitvalue(objvalue);
    [newpop] = selection(pop,fitvalue);
    [newpop] = crossover(pop,pc);
    [newpop] = mutation(pop,pc);
    [bestindividual,bestfit] = best(pop,fitvalue);
    y(i) = max(bestfit);
    n(i) = i;
    pop5 = bestindividual;
    x(i) = decodechrom(pop5,1,chromlength)*10/1023;
    pop = newpop;
end

fplot('9*sin(5*x) + 8*cos(4*x)',[0 15])
hold on
plot(x,y,'r*')
hold off

Running the main program, the results are as follows: