preface

Hello, I'm Xiaoxiong, a programmer from Huawei. Today, I bring you a high-frequency interview question related to binary tree. This question has been used as an interview question by big companies such as Google, byte, Microsoft and Amazon in half a year, that is, the 98th question on force buckle - Verifying binary search tree.

This paper mainly introduces two methods of recursion and depth first search to solve this problem for your reference. I hope it will be helpful to you.

Validate binary search tree

Give you the root node of a binary tree root ，Judge whether it is an effective binary search tree.

A valid binary search tree is defined as follows:

The left subtree of a node contains only a number smaller than the current node.

The right subtree of a node only contains a number greater than the current node.

All left and right subtrees themselves must also be binary search trees.

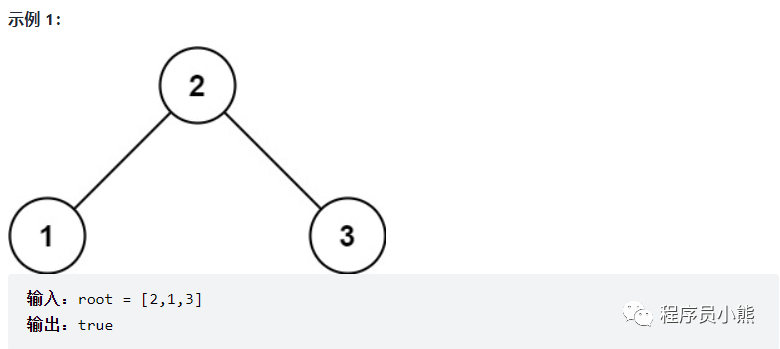
Example 1

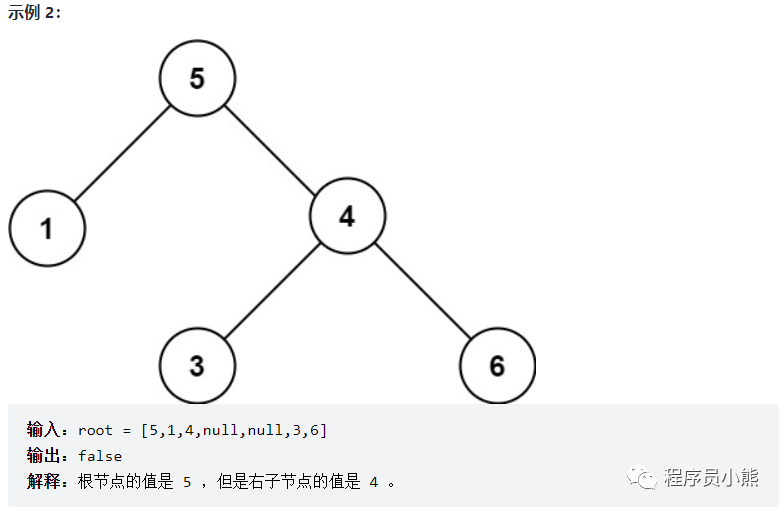
Example 2 and tips

Binary search tree

The title has prompted that the definition of effective binary search tree is as follows:

• The left subtree of a node contains only the number less than the current node.
• The right subtree of a node only contains a number greater than the current node.
• All left and right subtrees themselves must also be binary search trees.

give an example

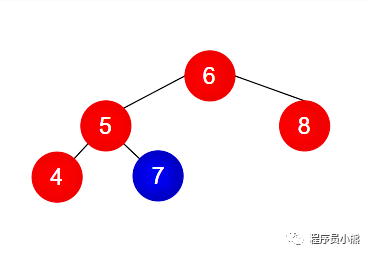
Example 1

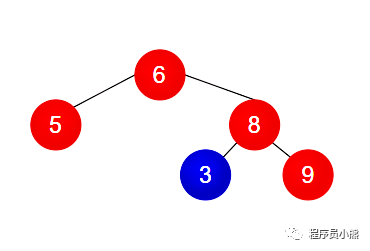
Example 2

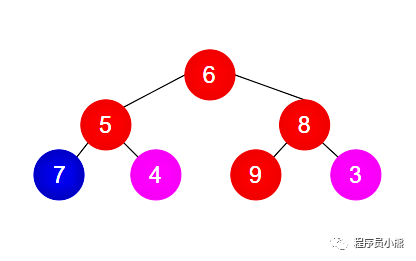
Example 3

Judgement binary search tree

For the above example, according to the judgment method of binary search tree, judge whether the above example is a binary search tree as follows:

1. Example 1 is not a binary search tree. Reason: the number of nodes (value 7) in the left subtree of the root node (value 6) is greater than the number of root nodes.
2. Example 2 is not a binary search tree. Reason: the number of nodes (value 3) in the right subtree of the root node (value 6) is less than the number of root nodes.
3. Example 3 is not a binary search tree. Reason: the left subtree of the root node is not a binary search tree, the value 5 of the root node of the left subtree is not only less than the value 7 of the left subtree, but also greater than the value 4 of the right subtree, and the value 6 of the root node is less than the value 7 of the node in the left subtree; The right subtree of the root node is also not a binary search tree. The value 8 of the root node of the right subtree is not only greater than the value 3 of the right subtree, but also less than the value 9 of the left subtree, and the value 6 of the root node is greater than the value 3 of the node in the right subtree.

Problem solving ideas

According to the definition of binary search tree, to judge whether a tree is a binary search tree, it is necessary to judge whether each node conforms to the nature of binary tree, and the judgment basis is the same. Therefore, the recursive method can be used to solve this problem.

recursion

The judgment basis mentioned above (assuming that the current node has left and right child nodes) refers to:

1. The value of the current node is greater than that of its left child node;
2. The value of the current node is less than that of its right child node;
3. If the current node has left and right subtrees, the nodes on the left and right subtrees should also meet the following requirements: all node values on the left subtree are less than those of the current node, and all node values on the right subtree are greater than those of the current node;

According to the above ideas, we can set the upper and lower bounds to judge whether the node conforms to the nature of binary search tree.

If there are upper and lower bounds, judge whether the node is within the upper and lower bounds. If it is not within the upper and lower bounds, it is not a binary search tree; Otherwise, take the value of the node as the upper bound to make recursive judgment on its left subtree, and take the value of the node as the lower bound to make recursive judgment on its right subtree.

be careful

An empty tree belongs to a binary search tree.

Show me the Code

C

bool isValidBST_Helper(struct TreeNode* root, double min, double max) {
    /* Special judgment */
    if (root == NULL) {
        return true;
    }

    /* The current node is not in the upper and lower bounds and is not a binary search tree */
    if (root->val <= min || root->val >= max) {
        return false;
    }

    /* Determine whether the left and right subtrees are binary search trees */
    return isValidBST_Helper(root->left, min, root->val) && isValidBST_Helper(root->right, root->val, max);
}

bool isValidBST(struct TreeNode* root) {
    return isValidBST_Helper(root, LONG_MIN, LONG_MAX);
}

C++

bool isValidBST_Helper(TreeNode* root, double min, double max) {
    if (root == nullptr) {
        return true;
    }

    if (root->val <= min || root->val >= max) {
        return false;
    }

    return isValidBST_Helper(root->left, min, root->val) && isValidBST_Helper(root->right, root->val, max);
}

bool isValidBST(TreeNode* root) {
    return isValidBST_Helper(root, LONG_MIN, LONG_MAX);
}

Java

boolean isValidBST_Helper(TreeNode root, double min, double max) {
    if (root == null) {
        return true;
    }

    if (root.val <= min || root.val >= max) {
        return false;
    }

    return isValidBST_Helper(root.left, min, root.val) && isValidBST_Helper(root.right, root.val, max);
}

boolean isValidBST(TreeNode root) {
    return isValidBST_Helper(root, Long.MIN_VALUE, Long.MAX_VALUE);
}

Python3

def isValidBST(self, root: TreeNode) -> bool:
    def isValidBST_Helper(root, min, right):
        if root is None:
            return True
        
        if root.val <= min or root.val >= right:
            return False

        return isValidBST_Helper(root.left, min, root.val) and isValidBST_Helper(root.right, root.val, right)

    return isValidBST_Helper(root, -float('inf'), float('inf')) 

Golang

func isValidBST(root *TreeNode) bool {
  return isValidBST_Helper(root, math.MinInt64, math.MaxInt64)
}

func isValidBST_Helper(root *TreeNode, min, max int) bool {
  if root == nil {
    return true
  }

  if min >= root.Val || max <= root.Val {
    return false
  }

  return isValidBST_Helper(root.Left, min, root.Val) && isValidBST_Helper(root.Right, root.Val, max)
}

Complexity analysis

Time complexity: O(n), where n is the number of binary tree nodes.

Space complexity: O(n).

Depth first search

According to the nature of binary search tree, the array obtained by middle order traversal must be arranged in ascending order. Therefore, we can judge whether a tree is a binary search tree according to this characteristic.

If the middle order traversal is adopted, the values of all nodes of the binary tree are stored in the array, and then judge whether the array is in ascending order, but the steps are a little cumbersome.

Because to judge whether the array is arranged in ascending order, you only need to judge whether the latter element of the array is successively greater than the previous element. Therefore, this problem can set a variable to save the value of the previous node traversed in the middle order, and then judge whether the value of the current node is greater than the value saved by the variable.

If not greater than, it means that the tree is not a binary search tree; Otherwise, continue to traverse and judge.

Show me the Code

C++

long pre = LONG_MIN;
bool isValidBST(TreeNode* root) {
    if (root == nullptr) {
        return true;
    }

    if (!isValidBST(root->left)) {
        return false;
    }

    if (root->val <= pre) {
        return false;
    }

    pre = root->val; 
    return isValidBST(root->right);      
}

Java

long temp = Long.MIN_VALUE;
boolean isValidBST(TreeNode root) {
    if (root == null) {
        return true;
    }

    if(!isValidBST(root.left)) {
        return false;
    }

    if (root.val <= temp) {
        return false;
    } 

    temp = root.val;
    return isValidBST(root.right);        
}

Complexity analysis

Time complexity: O(n), where n is the number of binary tree nodes.

Space complexity: O(n).