Interpolation search algorithm
Interpolation search algorithm, also known as interpolation search algorithm, is a search algorithm improved on the basis of binary search algorithm.
The interpolation search algorithm is only applicable to ordered sequences. In other words, it can only find the target elements in ascending or descending sequences. As an improved binary search algorithm, when the elements in the ordered sequence are evenly distributed, the search efficiency of the interpolation search algorithm is better than that of the binary search algorithm; On the contrary, if the ordered sequence does not meet the characteristics of uniform distribution, the search efficiency of interpolation search algorithm is not as good as binary search algorithm.
The so-called uniform distribution means that the difference of each adjacent element in the sequence is approximately equal. For example, {10, 20, 30, 40, 50} is a uniformly distributed ascending sequence, and the difference between adjacent elements is 10. For another example, {100, 500, 2000, 5000} is an ascending sequence, but the difference between adjacent elements is huge and does not have the characteristics of uniform distribution.
Solution of interpolation search algorithm
For readers who have learned the binary search algorithm, learning the interpolation search algorithm will become very easy, because the interpolation search algorithm completely copied the problem-solving idea of the binary search algorithm, and only modified some implementation details.
Firstly, we recall the problem-solving idea of binary search algorithm through an example. For example, find element 2 in {1,2,3,4,5,6,7,8,9,10} ascending sequence. The search process of binary search algorithm is shown in the following figure:

Figure 1 implementation process of binary search algorithm
As shown in Figure 1, first find the intermediate element in the search area, and then compare it with the target element. If it is the same, it indicates that the search is successful; On the contrary, select the area on the left or right of the intermediate element as the new search area according to the comparison results, and continue to search in the same way.
The solution idea of the interpolation search algorithm is almost the same as that of the binary search algorithm. The only difference is that the element compared with the target element each time is not an intermediate element in the search area. The position of this element needs to be calculated by the following formula:
Mid = Begin + ( (End - Begin) / (A[End] - A[Begin]) ) * (X - A[Begin])
In the formula, the meanings of each part are:
Mid: calculated element position;
End: the location of the last element in the search area;
Begin: the location of the first element in the search area;
10: The target element to find;
A []: indicates the whole sequence to be searched.
For the convenience of explanation, we still call the element at the Mid position "intermediate element".
Use the interpolation search algorithm to find element 2 in the {1,2,3,4,5,6,7,8,9,10} ascending sequence. The search process is as follows:
- Assuming that the position of each element in the sequence is 0 ~ 9 and the search area is the whole sequence, calculate the position of "intermediate element" through the formula:
Mid = 0 + ( (9-0)/(10-1) ) * (2-1) = 1
The position of "intermediate element" is 1, that is, element 2. Obviously, this is the target element we are looking for. The search is over. The whole search process is as follows:
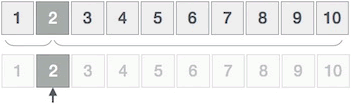
Figure 2 implementation process of interpolation search algorithm
Comparing Fig. 1 and Fig. 2, it is not difficult to see that in the ascending sequence of {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} satisfying uniform distribution, the execution efficiency of interpolation search algorithm is better than binary search algorithm.
Implementation of interpolation search algorithm
The specific implementation process of interpolation search algorithm is shown in the following pseudo code:
input arr[] // Input ordered sequence
input ele // Enter the target element to find
interpolation_search( arr , begin , end , ele): // [begin,end] specify the search area, and ele is the target element to search
// When [begin,end] does not exist, an error value is returned (for example, - 1)
if begin > end:
return -1
// When [begin,end] contains only one element, judge whether this element is a target element
if begin == end:
if ele == arr[begin]:
return begin
else:
return -1
// Find the subscript of the "intermediate value" in the [begin,end] area
mid <- begin + ( (end-begin)/(arr[end] - arr[begin]) * (ele - arr[begin]) )
// The exit of recursion, that is, the values of ele and intermediate elements are equal
if ele == arr[mid]:
return mid
if ele < arr[mid]: // Compare the values of ele and intermediate elements to further narrow the search area
return binary_search(arr , begin , mid-1 , ele)
else:
return binary_search(arr , mid+1 , end , ele)
Combined with pseudo code, the following is a C language program for finding element 2 in {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} sequence using interpolation search algorithm:
#include <stdio.h>
//Implement the interpolation search algorithm. ele represents the target element to be searched, [begin,end] specifies the search area
int interpolation_search(int* arr, int begin, int end, int ele) {
int mid = 0;
//If [begin,end] does not exist, - 1 is returned
if (begin > end) {
return -1;
}
//If there is only one element in the search area, judge whether it is the target element
if (begin == end) {
if (ele == arr[begin]) {
return begin;
}
//If the element is not the target element, the lookup fails
return -1;
}
// Find the location of the "intermediate element"
mid = begin + ((end - begin) / (arr[end] - arr[begin]) * (ele - arr[begin]));
//Recursive exit
if (ele == arr[mid]) {
return mid;
}
//Compare the values of ele and arr[mid] to narrow the area where ele may exist
if (ele < arr[mid]) {
//The new search area is [begin,mid-1]
return interpolation_search(arr, begin, mid - 1, ele);
}
else {
//The new search area is [mid+1,end]
return interpolation_search(arr, mid + 1, end, ele);
}
}
int main()
{
int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
//The subscript of the location of the output element 2
int pos = interpolation_search(arr, 0, 9, 2);
if (pos != -1) {
printf("%d", interpolation_search(arr, 0, 9, 2));
}
else {
printf("Search failed");
}
return 0;
}
The following is a Java program that uses the interpolation search algorithm to find element 2 in the {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} sequence:
public class Demo {
// Implement the interpolation search algorithm. ele represents the target element to be searched, [begin,end] specifies the search area
public static int interpolation_search(int[] arr, int begin, int end, int ele) {
// If [begin,end] does not exist, - 1 is returned
if (begin > end) {
return -1;
}
//If there is only one element in the search area, judge whether it is the target element
if (begin == end) {
if (ele == arr[begin]) {
return begin;
}
//If the element is not the target element, the lookup fails
return -1;
}
// Find the location of the intermediate element
int mid = begin + ((end - begin) / (arr[end] - arr[begin]) * (ele - arr[begin]));
// Recursive exit
if (ele == arr[mid]) {
return mid;
}
// Compare the values of ele and arr[mid] to narrow the area where ele may exist
if (ele < arr[mid]) {
// The new search area is [begin,mid-1]
return interpolation_search(arr, begin, mid - 1, ele);
} else {
// The new search area is [mid+1,end]
return interpolation_search(arr, mid + 1, end, ele);
}
}
public static void main(String[] args) {
int[] arr = new int[] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
// Output the subscript of the location of the target element 2
int add = interpolation_search(arr, 0, 9, 2);
if(add != -1) {
System.out.print(add);
}else {
System.out.print("Search failed");
}
}
}
The following is a Python program that uses the interpolation search algorithm to find element 2 in the {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} sequence:
#Implement the interpolation search algorithm. ele represents the target element to be searched, [begin,end] specifies the search area
def interpolation_search(arr,begin,end,ele):
#If [begin,end] does not exist, - 1 is returned
if begin > end:
return -1
if begin == end:
if arr[begin] == ele:
return begin
return -1
#Find the location of the intermediate element
mid = int(begin + ((end - begin) / (arr[end] - arr[begin]) * (ele - arr[begin])))
#Recursive exit
if ele == arr[mid]:
return mid
#Compare the values of ele and arr[mid] to narrow the area where ele may exist
if ele < arr[mid]:
return interpolation_search(arr,begin,mid-1,ele)
else:
return interpolation_search(arr,mid+1,end,ele)
arr = [1,2,3,4,5,6,7,8,9,10]
#The subscript of the location of the output element 2
add = interpolation_search(arr, 0, 9, 2);
if add != -1:
print(add)
else:
print("Search failed")
The output results of the above procedures are:
1