A HashMap HashTable HashSet
HashMap is a hash table that stores key value mappings. It inherits from AbstractMap and implements Map, Cloneable and Serializable interfaces. The implementation of HashMap is not synchronous, which means that it is not thread safe. Its key and value can be null. The mappings in HashMap are not ordered.
JDK1. In 6, HashMap is implemented by array + linked list, that is, the linked list is used to deal with conflicts, and the linked lists of the same hash value are stored in a linked list. However, when there are many elements in an array, that is, there are many elements with equal hash values, the efficiency of searching by key values in turn is low. And jdk1 In 8, HashMap is implemented by array + linked list + red black tree. When the length of the linked list exceeds the threshold of 8, the linked list is converted into red black tree, which greatly reduces the search time. Original map The implementation class of the Entry interface is renamed Node. When converting to red black tree, use another method to implement TreeNode.
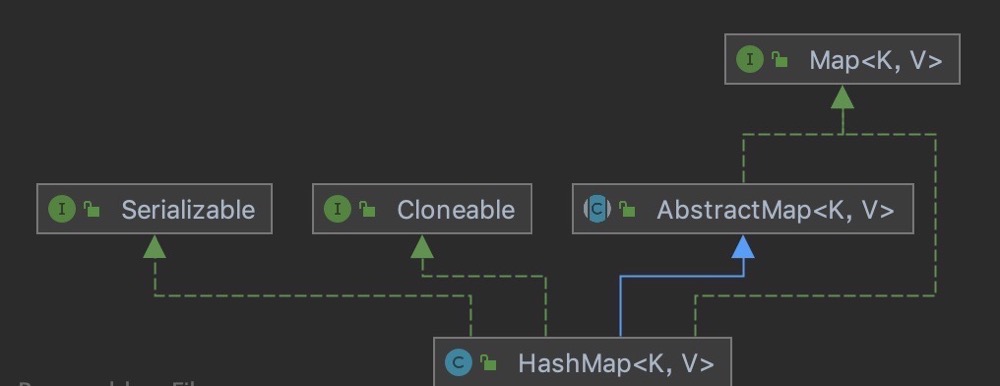
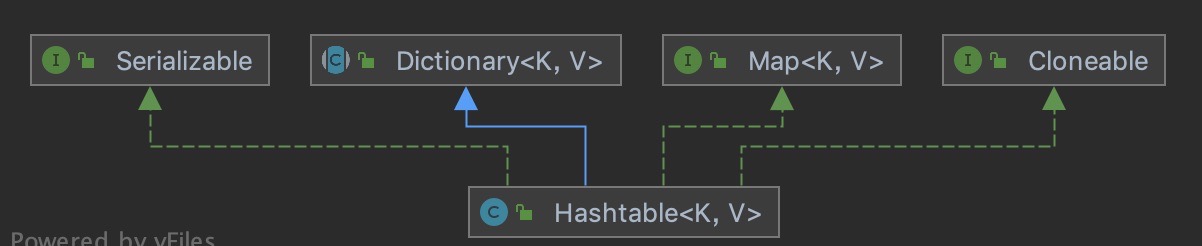
The internal implementation of Hashtable is basically the same as that of HashMap, except that the synchronized keyword is added to the methods to ensure thread safety; Its key and value cannot be null; The capacity expansion methods of Hashtable and HashMap are different. The default size of the array in Hashtable is 11, and the capacity expansion method is old*2+1.
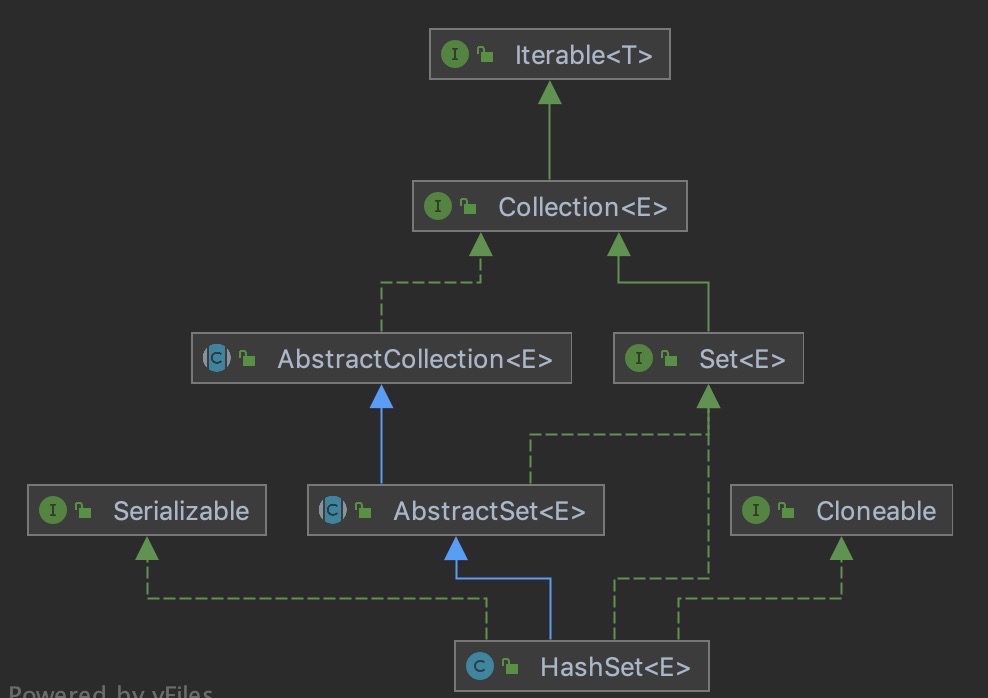
HashSet inherits AbstractSet and implements set, Cloneable and serializable. The internal implementation depends on HashMap. There is a HashMap (adapter mode) in HashSet, so the structure of HashSet is relatively simple. The iteration order of elements is not guaranteed to remain unchanged, and a null is allowed. Non thread safe.
To sum up, we can see that HashMap is the core of these three sets, which are implemented around this idea or source code. We will introduce the source code of HashMap in detail. HashTable HashSet can understand the difference between them and HashMap.
II. Differences between HashMap hashtable and HashSet
The difference between HashMap and HashTable: the internal implementation is basically the same. HashMap key value can be null, but HashTable cannot; Their default array length is different. The default array length of HashMap is 16 and that of HashTable is 11; The capacity expansion methods are different. The capacity expansion of HashMap is twice that of the original, and the capacity expansion of HashTable is old*2+1.
The difference between HashMap and HashSet: HashMap implements the Map interface and HashSet implements the Set interface; HashMap stores key value pairs, and HashSet stores objects; HashMap will calculate the hash for the key, while HashSet calculates the hash for the object (because it only has objects). In fact, HashSet stores the object as the key of HashMap.

III. HashMap constant definition
// The default initial capacity must be a power of 2, and the default is 16 static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // Maximum capacity (must be a power of 2 and less than the 30th power of 2. If too much capacity is passed in the constructor, the parameter will be replaced by this value) static final int MAXIMUM_CAPACITY = 1 << 30; // Default load factor. What is load factor? HashMap calculates the maximum number of elements that can be accommodated by the load factor and the number of buckets // The calculation formula is threshold = capacity * loadFactor static final float DEFAULT_LOAD_FACTOR = 0.75f; // Threshold value of converting linked list into red black tree static final int TREEIFY_THRESHOLD = 8; // The threshold at which the red black tree is transformed into a linked list can only occur during capacity expansion static final int UNTREEIFY_THRESHOLD = 6; // The minimum capacity of tree to prevent conflict when adjusting capacity and shape static final int MIN_TREEIFY_CAPACITY = 64;
Four construction methods
The constructor does not initialize the array and internal node class. The object is instantiated only when the element is added for the first time. The constructor only assigns a constant value
// Specify initialization length and expansion factor
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
// If it is greater than the 30th power of 2, the default value is the 30th power of 2
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
// Specify the initial length (internally call the construction method of the upper edge, and the expansion factor uses the default)
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
// Default assignment expansion factor
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
V. new methods
Calculate the hash of the key and perform XOR displacement operation (scatter the key to different arrays); If it is added for the first time, initialize the array. Otherwise, insert the array index value calculated according to the key. If the current array is empty, insert it directly. If the current array element is a red black tree, insert it using the red black tree. Otherwise, it is a linked list structure. Traverse the linked list, insert the tail, and replace it directly if duplicate keys are found during traversal; Finally, judge whether the threshold is exceeded and whether to expand the capacity
// Add key
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
// After calculating the hash of the key; The high 16 bits remain unchanged, and the XOR of the low 16 bits and the high 16 bits is the final hash value of the key;
// The reason for this setting is that the subscript is calculated as: n = table length; index = (n-1) & hash;
// The length of the table is a power of 2, so the index is only related to the lower n bits of the hash value
// The high order of the hash value is set to 0 with the operation, so XOR reduction conflicts
// The desired effect is to scatter the key s into different arrays as much as possible
// Moreover, when expanding the capacity, it can ensure that the value of the current array linked list stays in the current array or twice the current array
// For example, the key is initially saved in a linked list with an array subscript of 2. After the expansion, the linked list data with an array subscript of 2 is either in a position with an array subscript of 2 or in a position with an array subscript of 18
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
// If the fourth parameter onlyIfAbsent is true, the put operation will be performed only when the key does not exist
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// The first time you put a value, the following resize() will be triggered
// The first resize is somewhat different from the subsequent expansion, because this time the array is initialized from null to the default 16 or custom initial capacity
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// According to the hash value of the key, get the inserted array index I. If table[i]==null, directly create a new node and add it
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
// Otherwise, there is data here
else {
Node<K,V> e; K k;
// Judge whether the first node is equal to the current value. If it is equal, replace it directly
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// Judge whether the current linked list is a red black tree
else if (p instanceof TreeNode)
// It's a red black tree. It's directly inserted into the red black tree
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// This judgment represents a linked list structure
else {
// Traverse table[i]
for (int binCount = 0; ; ++binCount) {
// Insert to the back of the linked list (Java 7 is the front of the linked list); If the length of the linked list is less than 8, execute the insertion operation of the linked list
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
// If the length of the linked list is greater than or equal to 8, convert the linked list into a red black tree and perform the insertion operation
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// During traversal, if the key is found to exist, the value will be overwritten directly
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// If the key already exists, replace the original value with a new value and return the original value
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
// After successful insertion, judge whether the actual number of key value pairs exceeds the maximum capacity threshold. If it exceeds the maximum capacity threshold, call re size to expand the capacity
// A little different from Java 7 is that Java 7 expands the capacity first and then inserts new values, and Java 8 interpolates and then expands the capacity
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
Vi. resize() method
Initialize or expand the size. If it is blank, it is allocated according to the initial capacity target held in the field threshold. Otherwise, because we use the power expansion of 2, the elements in each array remain in the original array or move at the offset of the power of 2 in the newly expanded array (for example, a, b and c stay on array 1 before expanding 16 lengths, or stay at 1 or 17)
Judge whether the length of the current array is the maximum length. If it is the maximum length, the capacity will not be expanded and the original array will be returned; If not, expand the capacity to twice the original; Then judge whether to initialize the insertion. If so, initialize the array of length; Otherwise, you need to expand the capacity twice as much as the original, traverse the old table and store it in two linked lists, the original position linked list and the new position linked list (because the high and low order operation of the power of 2 is used, it will only stay in the original position and the position after capacity expansion). Judge whether it is stored in different linked lists and insert it into the corresponding array position after capacity expansion
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
// If the array size before expansion exceeds the maximum capacity
if (oldCap >= MAXIMUM_CAPACITY) {
// Modify the resize threshold to the maximum value of int (2 ^ 31-1), so that the capacity will not be expanded in the future
threshold = Integer.MAX_VALUE;
// Return the original array directly
return oldTab;
}
// Without exceeding the maximum capacity, expand the capacity to twice the original capacity
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// The new resize threshold is also doubled
newThr = oldThr << 1; // double threshold
}
// Corresponding to the first put after new HashMap(int initialCapacity) initialization
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
// Corresponding to the first put after initialization with new HashMap()
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// Calculate a new resize threshold
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
// Initializes a new array with the new array size
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
// If you are initializing an array, this is the end, and you can return newTab
table = newTab;
if (oldTab != null) {
// Traverse old table
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
// Release the object reference of the old table (after the for loop, the old table no longer references any objects)
oldTab[j] = null;
// If oldTab[j] contains only one element
if (e.next == null)
// Put this element directly in the appropriate position of newTab
newTab[e.hash & (newCap - 1)] = e;
// If the oldTab[j] storage structure is a red black tree, perform the adjustment operation in the red black tree
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
// If the oldTab[j] storage structure is a linked list
// You need to split the linked list into two linked lists, put them into a new array, and keep the original order
// There is no need to recalculate the position of elements in the array. The position is calculated by adding the original position to the length of the original array
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
// Whether the position of the element in the array needs to be moved can be obtained through bit operation
if ((e.hash & oldCap) == 0) {
// When the linked list is empty, the current node is set as the head node
if (loTail == null)
loHead = e;
// If it is not empty, the next node of the tail node is set as the current node
else
loTail.next = e;
// Set the tail node as the current node and move the pointer
loTail = e;
}
// When you need to move
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}VII. Search method
Calculate the hash of the query key, calculate the current array position, and judge whether it is empty; If it is not empty, judge whether the first element of the current array linked list is empty; Judge whether the current element needs to be queried. If yes, return; Otherwise, judge whether the next node of the first node is empty; Judge whether the current linked list is a red black tree. The red black tree uses the red black tree query method to query the elements; Otherwise, if you traverse the current linked list and judge that the equals method is equal, it returns.
public V get(Object key) {
Node<K,V> e;
// Find the hash value of the key and call getNode
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// When the table is not empty and the calculated insertion position table[i] is not empty, continue the operation, otherwise null will be returned
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// Judge whether the first element of table[i] is equal to key, and if so, return it
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
// If the storage structure is a red black tree, perform the search operation in the red black tree
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
// If the storage structure is still a linked list, traverse the linked list to find the location of the key
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}VIII. Hashmap1 Differences between 7 and 1.8
1. The implementation methods are different. 1.7 uses array and linked list, and 1.8 uses array and linked list and red black tree; Why do you do this optimization? First, the length of the linked list is too long, which affects the query efficiency. Converting to red black tree can improve the query efficiency; Second, the linked list is easy to form a circular linked list during high concurrent capacity expansion. This problem can be avoided by using the high and low positions in the capacity expansion of red black tree
2. The hash algorithm is simplified. The 1.7 hash algorithm is complex because it is necessary to scatter the data as much as possible to improve the query efficiency. However, the red black tree is introduced in 1.8. At the same time, the hash algorithm is optimized for XOR and shift right operations, which can better realize the fragmentation
3. The insertion positions are different. 1.7 adopts the head insertion method and 1.8 adopts the tail insertion method; Because the number of elements in the linked list is not recorded in 1.8, it is not determined whether to convert the red black tree or the linked list until the insertion is completed
4. The capacity expansion methods are different. 1.7 capacity expansion needs to recalculate the hash and traverse to the new linked list, and the linked list will be reversed, so it is easy to form a circular linked list under concurrency; 1.8 insert a new linked list in sequence through the algorithm of too high and low order, and there will be no circular linked list