The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:

• Every candidate can place exactly one poster on the wall.
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
• The wall is divided into segments and the width of each segment is one byte.
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers li and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= li <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered li, li+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed.

The picture below illustrates the case of the sample input.

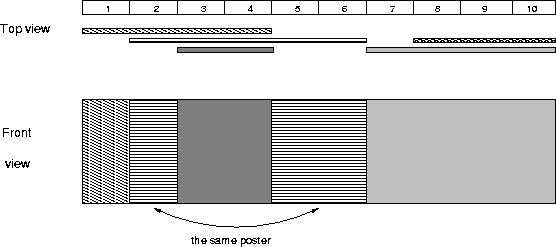
Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

  Meaning:   There are n operations. Each operation will paint colors on a series of squares numbered [l, r]. The newly painted colors will cover the previously painted colors. The colors painted in each operation are different. Ask how many different colors can be seen in the end (not painted is not a color).

Analysis: for the obvious interval coverage problem, if the data range is not considered, this problem only needs to use the segment tree to maintain the interval sum that supports interval modification and interval query. However, since the values of l and r may be very large and the number is relatively small, they cannot be directly connected to the segment tree, so discretization can be considered first. The discretization here is special, especially for interval discretization. In fact, like the discretization of points, it is necessary to ensure that the relative position relationship before and after discretization remains unchanged. The difference is that the interval discretization here should consider whether the two points are actually adjacent, if they are adjacent, they should also be adjacent after discretization. If they are not adjacent, they should also be kept not adjacent after discretization. Two counterexamples are given respectively. The counterexamples of the former are: the first painting [1,4], the second painting [1,2], the third painting [3,4], and the error discretization is [1,7], [1,3], [5,7]. The counterexamples of the latter are: the first painting [1,6], the second painting [1,2], the third painting [5,6], and the error discretization is [1,4], [1,2], [3,4]. The correct method is: add all points to the vector and scan the vector again. If the two adjacent points are numerically adjacent, they will not be processed. If they are numerically separated, add a point, indicating that the two points are actually separated.

The specific codes are as follows:

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
//After all points are added to the vector, the originally adjacent two points should continue to be adjacent
//And the originally separated two points should be inserted into a point, so that lower_ Only when bound is found is the subscript separated 
int n, sum[80005], lazy[80005];
vector<int> alls;

int find(int x)
{
	return lower_bound(alls.begin(), alls.end(), x)-alls.begin()+1;
} 

void push_down(int id, int ln, int rn)
{
	if(lazy[id])
	{
		lazy[id<<1] = lazy[id];
		lazy[id<<1|1] = lazy[id];
		sum[id<<1] = lazy[id]*ln;
		sum[id<<1|1] = lazy[id]*rn;
		lazy[id] = 0;
	}
}

void push_up(int id)
{
	sum[id] = sum[id<<1]+sum[id<<1|1];
}

void update(int L, int R, int C, int l, int r, int id)
{
	if(L == l && R == r)
	{
		sum[id] = C*(r-l+1);
		lazy[id] = C;
		return;
	}
	int m = l+r>>1;
	push_down(id, m-l+1, r-m);
	if(R <= m)
		update(L, R, C, l, m, id<<1);
	else if(L >= m+1)
		update(L, R, C, m+1, r, id<<1|1);
	else
		update(L, m, C, l, m, id<<1), update(m+1, R, C, m+1, r, id<<1|1);
	push_up(id);
}

int query(int L, int R, int l, int r, int id)
{
	if(L == l && R == r)
		return sum[id];
	int m = l+r>>1;
	push_down(id, m-l+1, r-m);
	if(R <= m)
		return query(L, R, l, m, id<<1);
	else if(L >= m+1)
		return query(L, R, m+1, r, id<<1|1);
	else
		return query(L, m, l, m, id<<1)+query(m+1, R, m+1, r, id<<1|1);

}

signed main()
{
	int T;
	cin >> T;
	while(T--)
	{
		cin >> n;
		memset(lazy, 0, sizeof lazy);
		memset(sum, 0, sizeof sum);
		alls.clear();
		int l[10005], r[10005];
		int a[20005];//Points to be discretized
		int cnt = 0; 
		for(int i = 1; i <= n; i++)
		{
			scanf("%d%d", &l[i], &r[i]);
			alls.push_back(l[i]);
			alls.push_back(r[i]);
		}	
		sort(alls.begin(), alls.end());
		alls.erase(unique(alls.begin(), alls.end()), alls.end());
		int len = alls.size();
		for(int i = 1; i < len; i++)
			if(alls[i-1]-alls[i] > 1)
				alls.push_back(a[i]-1);
		sort(alls.begin(), alls.end());
		for(int i = 1; i <= n; i++)
		{
			int ll = find(l[i]);
			int rr = find(r[i]);
			update(ll, rr, i, 1, alls.size(), 1); 
		}
		int ans = 0, vis[10005] = {0};//The answer is the number of different numbers in the interval 
		for(int i = 1; i <= alls.size(); i++)
		{
			int temp = query(i, i, 1, alls.size(), 1);
			if(temp == 0)
				continue;
			if(vis[temp] == 0)
			{
				vis[temp] = 1;
				ans++;
			}
		}
		cout << ans << endl;
	} 
	return 0;
}