[interview questions] width first search
1, The most concise general template of BFS algorithm
1. BFS templates for trees and graphs
- new ArrayDeque is recommended for queues, and new LinkedList is not recommended (linked list is slower than array)
//Double ended queue
Queue<Node> queue = new ArrayDeque<>();
HashMap<Node,Integer> distance = new HashMap<>();
//step 1 initialization
//Put the initial node in deque. If there are multiple nodes, put them in
//Mark the distance of the initial node as 0 and record it in the hashmap of distance
//Distance has two functions: one is to judge whether it has been visited, and the other is to record the distance from the starting point
queue.offer(node);
distance.put(node,0);
//step 2: continuously accessing the queue
//while loop + one point in each pop queue
while (!queue.isEmpty()) {
Node node = queue.poll();
//step 3: expand adjacent nodes
//pop out the adjacent nodes of the node, join the queue and store examples in distance
for (Node neighbor : node.getNeighbors()) {
continue;
}
distance.put(neighbor, distance.get(node) + 1);
queue.offer(neighbor);
}
- Complexity: BFS time complexity on the graph = O(N + M)
2,LeetCode-133. Clone graph
- [title link]( 133. Clonal diagram - LeetCode (LeetCode CN. Com))
class Solution {
public Node cloneGraph(Node node) {
//Special case handling
if (node == null) {
return null;
}
//Step 1: find all points
List<Node> nodes = findNodesByBFS(node);
//Step 2: copy all points
Map<Node, Node> mapping = copyNodes(nodes);
//Part 3: copy all edges
copyEdges(nodes, mapping);
//Returns the node with the same val as the given node
return mapping.get(node);
}
//Step 1: BFS find all points
private List<Node> findNodesByBFS(Node node) {
Queue<Node> queue = new LinkedList<>();
//Used to save all points without repetition or omission
Set<Node> visited = new HashSet<>();
queue.offer(node);
//Once you join the team, mark it immediately
visited.add(node);
while(!queue.isEmpty()) {
Node curNode = queue.poll();
for (Node neighbor : curNode.neighbors) {
//If this point has been found before, there is no need to BFS again, otherwise the loop is dead
if (visited.contains(neighbor)) {
continue;
}
//Once accessed, it should be marked immediately.
visited.add(neighbor);
queue.offer(neighbor);;
}
}
return new LinkedList<>(visited);
}
//Step 2: copy all points
private Map<Node,Node> copyNodes(List<Node> nodes) {
//(old point - > new point) mapping
Map<Node,Node> mapping = new HashMap<>();
for (Node node : nodes) {
mapping.put(node, new Node(node.val));
}
return mapping;
}
//Step 3: copy all edges
private void copyEdges(List<Node> nodes, Map<Node,Node> mapping) {
for (Node node : nodes) {
Node newNode = mapping.get(node);
//The old point has neighbors, and the new point has neighbors
for (Node neighbor : node.neighbors) {
Node newNeighbor = mapping.get(neighbor);
newNode.neighbors.add(newNeighbor);
}
}
}
}
- As can be seen from the above code, the most important thing is to find all points through BFS.
3,LeetCode-127. Word Chain
- [title link]( 127. Word: LeetCode (LeetCode CN. Com))
① Generate transform list


② Transform list diagram
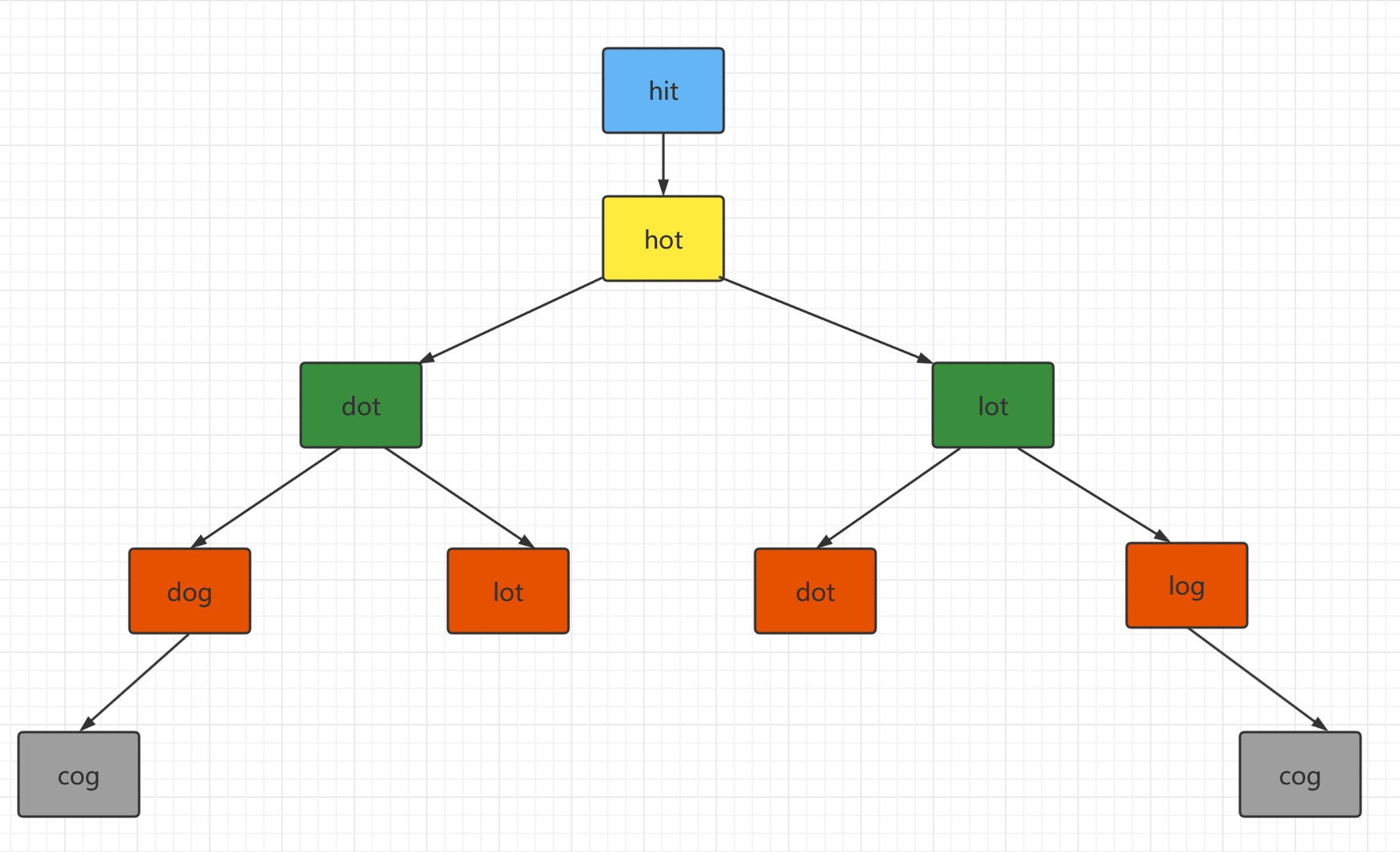
③ Code implementation
class Solution {
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
//Assume wordList is not empty
//Suppose beginWord and endWord are non empty and different
//You must join endWord. Can join beginword
wordList.add(endWord);
HashSet<String> visited = new HashSet<String>();
Queue<String> queue = new LinkedList<String>();
queue.offer(beginWord);
visited.add(beginWord);
//Record the shortest route length, starting at 1
int length = 1;
while(!queue.isEmpty()) {
//The length to the next layer (not the current layer), which is equivalent to the depth of the tree
length++;
//The current layer has size elements
int size = queue.size();
for (int i = 0; i < size; i++) {
String word = queue.poll();
//Get the next word
for (String nextWord : getNextWords(word,wordList)) {
if (visited.contains(nextWord)) {
continue;
}
//If the word of the next layer is the last word, the current length to the next layer (not the current layer) is returned directly
if (nextWord.equals(endWord)) {
return length;
}
//Join the next layer to prepare for the later BFS
visited.add(nextWord);
queue.offer(nextWord);
}
}
}
//Can't connect head to tail
return 0;
}
//Find all the words that can connect with word
//For example, word = 'hot', dict = {hot ',' hit ',' hog '}, return ['hit', 'hog']
private ArrayList<String> getNextWords(String word, List<String> wordList) {
ArrayList<String> nextWords = new ArrayList<String>();
//Enumerate each word in the dictionary
for (String nextWord : wordList) {
boolean hashOneDiff = false;
for (int i = 0; i < word.length(); i++) {
//Judge whether two words differ by only one letter. If yes, it can be connected
if (nextWord.charAt(i) != word.charAt(i)) {
//If there is already a difference, eliminate it directly
if (hashOneDiff) {
hashOneDiff = false;
break;
}
hashOneDiff = true;
}
}
if (hashOneDiff) {
nextWords.add(nextWord);
}
}
return nextWords;
}
//New string
private String replace(String word, int index, char c) {
char[] chars = word.toCharArray();
chars[index] = c;
return new String(chars);
}
}
2, Width first search in matrix
1,LeetCode-200. Number of islands
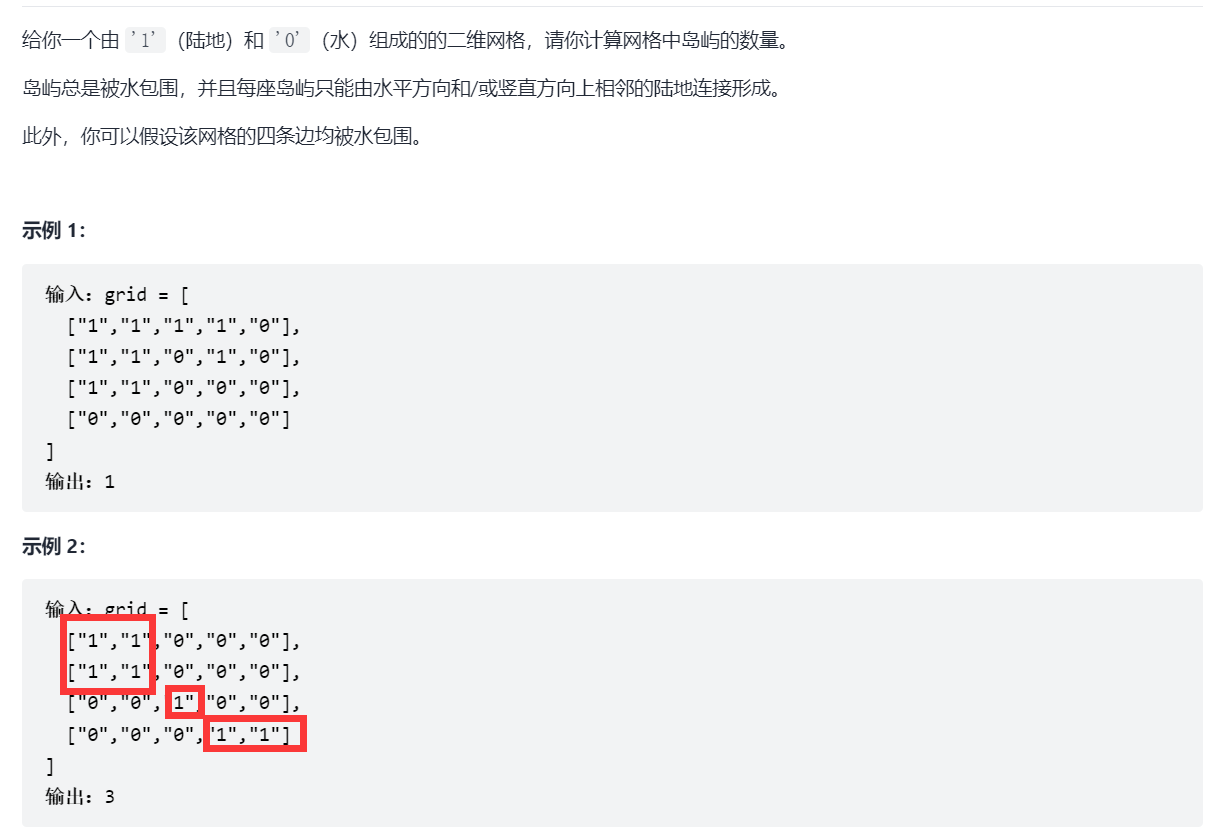
Train of thought analysis

code implementation
//Define a class to represent a point in the coordinate system
class Coordinate {
int x, y;
public Coordinate(int x, int y) {
this.x = x;
this.y = y;
}
}
class Solution {
//Offset in four directions
int[] deltaX = {0, 1, -1, 0};
int[] deltaY = {1, 0, 0, -1};
public int numIslands(char[][] grid) {
//Special case handling
if (grid == null || grid.length == 0 || grid[0] == null || grid[0].length == 0) {
return 0;
}
int islands = 0;
int row = grid.length, col = grid[0].length;
//Record whether a point has been BFS. If it has been BFS before, it should not be BFS again
boolean[][] visited = new boolean[row][col];
//Traverse every point in the matrix
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
//In case of ocean, BFS is not required
//If the point has been visited, there is no need for redundant traversal and repeated reading
if (grid[i][j]!='0' && !visited[i][j]) {
bfs(grid, i, j, visited);
islands++;
}
}
}
return islands;
}
//Start from a piece of land and traverse the whole island through BFS
private void bfs(char[][] grid, int x, int y, boolean[][] visited) {
Queue<Coordinate> queue = new ArrayDeque<>();
queue.offer(new Coordinate(x, y));
visited[x][y] = true;
while (!queue.isEmpty()) {
Coordinate coor = queue.poll();
//Traverse up, down, left and right directions
for (int direction = 0; direction < 4; direction++) {
int newX = coor.x + deltaX[direction];
int newY = coor.y + deltaY[direction];
//If it is not a valid point, continue
if (!isValid(grid, newX, newY, visited)) {
continue;
}
queue.offer(new Coordinate(newX, newY));
//Once you join the team, mark that this store has participated in BFS
visited[newX][newY] = true;
}
}
}
//Judge whether a point can be BFS
private boolean isValid(char[][] grid, int x, int y, boolean[][] visited) {
int n = grid.length, m = grid[0].length;
//If out of bounds, return false
if (x < 0 || x>=n || y < 0 || y >= m) {
return false;
}
//If you have BFS, do not BFS again, avoid: 1 Dead cycle 2 Redundant BFS variables
if (visited[x][y]) {
return false;
}
//true if '1'; false if 0
return grid[x][y] == '1' ? true : false;
}
}
Reflection record
- Deal with the problem of matrix, the simulation of up, down, left and right coordinate movement, through the offset.
- Traverse the surrounding islands and use BFS.
- The processing of details, the representation of points in the coordinate system, the transfer method of visited array (avoiding the use of global variables), and the detection and judgment of boundary values.
- The ArrayDeque class is used in the queue when implementing BFS.
2,LintCode-611. The shortest route for a knight
- [title link]( 611. Knight's shortest route - LintCode)
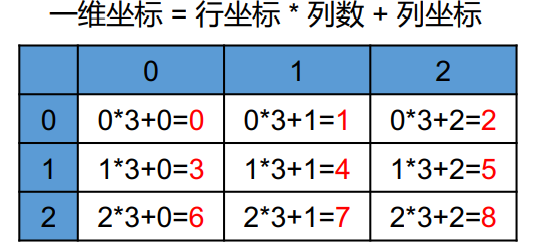
- One dimensional coordinates have unique certainty
/**
* Definition for a point.
* class Point {
* int x;
* int y;
* Point() { x = 0; y = 0; }
* Point(int a, int b) { x = a; y = b; }
* }
*/
public class Solution {
//Offset in 8 directions, which can be moved by the knight
public static final int[] X_OFFSET = {1, 1, -1, -1, 2, 2, -2, -2};
public static final int[] Y_OFFSET = {2, -2, 2, -2, 1, -1, 1, -1};
public int shortestPath(boolean[][] grid, Point source, Point destination) {
//exception handling
if (grid == null || grid.length == 0 || grid[0] == null || grid[0].length == 0) {
return -1;
}
Queue<Point> queue = new ArrayDeque<>();
//Record the shortest distance from the starting point to (x,y), (x,y) represents the shortest distance to the starting point start
Map<Integer,Integer> cellToDisMap = new HashMap();
int col = grid[0].length;
queue.offer(source);
//Multiply by col to avoid repetition, and replace two-dimensional coordinates with one-dimensional coordinates
cellToDisMap.put(source.x * col + source.y, 0);
while (!queue.isEmpty()) {
Point point = queue.poll();
int curPointKey = point.x * col + point.y;
if (point.x == destination.x && point.y == destination.y) {
return cellToDisMap.get(curPointKey);
}
//Traverse 8 different directions
for (int i = 0; i < 8; i++) {
int adjX = point.x + X_OFFSET[i];
int adjY = point.y + Y_OFFSET[i];
if (!isValid(adjX, adjY, grid)) {
continue;
}
//Small routine: convert two-dimensional coordinates into one-dimensional coordinates
int newPointKey = adjX * col + adjY;
//If this point has been reached before, it is impossible to find the shortest path at this point of BFS again, which will also cause dead cycle
if (cellToDisMap.containsKey(newPointKey)) {
continue;
}
queue.offer(new Point(adjX, adjY));
cellToDisMap.put(newPointKey, cellToDisMap.get(curPointKey) + 1);
}
}
return -1;
}
private boolean isValid(int x, int y, boolean[][] grid) {
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length) {
return false;
}
//A value of 1 indicates an obstacle and returns false
return !grid[x][y];
}
}
3, Topological Sorting
1. What is topological sorting
In a directed graph, all nodes are sorted, and no node is required to point to the node in front of it.
First count the penetration of all nodes. The nodes with penetration of 0 can be separated, and then reduce the penetration of the node pointed to by this node by one.
Repeat the above operation until all nodes are separated.
If there is no node with a degree of 0 at last, it indicates that there is a ring and there is no topological sorting, that is, there is no solution.
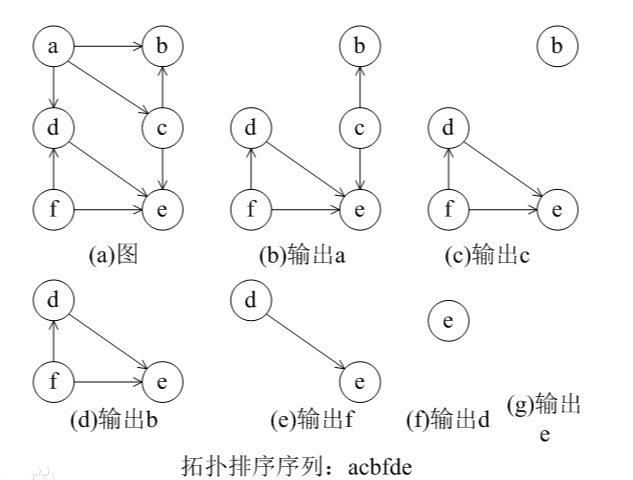
Detailed description:
- Count the penetration of each point
- Put each point with a penetration of 0 into the queue as the starting node.
- Constantly take out a point from the queue, remove all the connected edges of this point (the edges pointing to other points), and the corresponding penetration of other points is - 1
- Once a new point with a penetration of 0 is found, it is thrown back into the queue.
2,LeetCode-207. Class Schedule Card
[title link]( 207. Curriculum - LeetCode (LeetCode CN. Com))
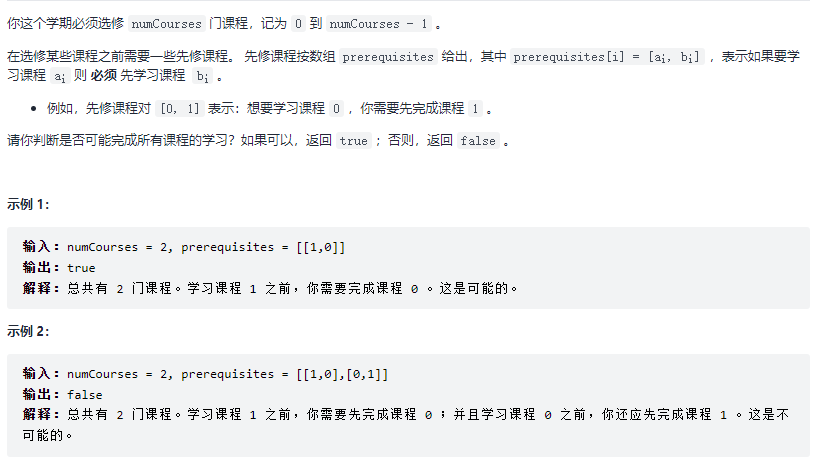
Problem solving ideas:
Graph + dependency + directed + (ring) = topological sorting
- Count the penetration of each point
- Put each point with 0 in degree into the queue as the starting node
- Constantly take out a point from the queue, remove all the connected edges of this point (the edges pointing to other points), and the corresponding penetration of other points is - 1
- Once a new point with a penetration of 0 is found, it is thrown back into the queue.
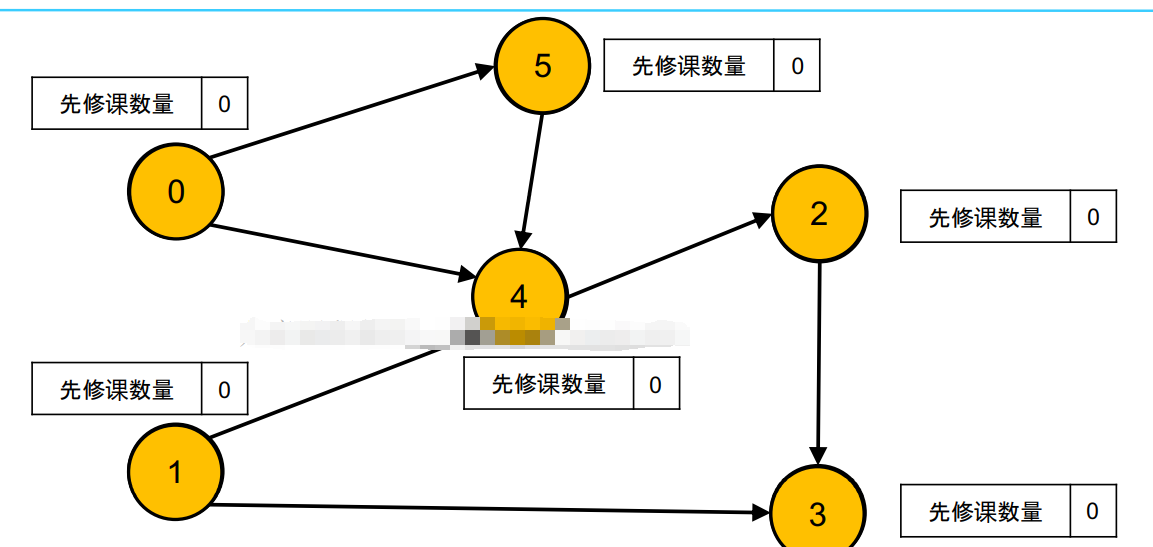
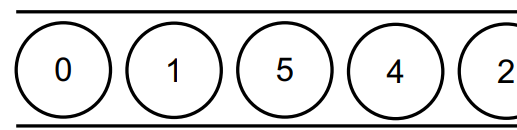
Code implementation:
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
//Construction diagram, representing the mapping of (pre courses - > multiple post courses)
List[] graph = new ArrayList[numCourses];
//Initialization of diagram, each course - > empty course List
for (int i = 0; i < numCourses; i++) {
graph[i] = new ArrayList<Integer>();
}
//1. Count the penetration of each point and build a graph
int[] inDegree = new int[numCourses];
for (int[] edge : prerequisites) {
//For example [0,1]: if you want to take course 0, learn course 1 first, then the entry of 0 will be increased by 1.
//That is, the arrow of the directed graph indicates the dependency. You can only take course 0 after taking course 1
//Note that here is the mapping of courses to be taken first - > courses to be taken later, i.e. courses to be taken or courses to be taken later
graph[edge[1]].add(edge[0]);
inDegree[edge[0]]++;
}
Queue queue = new LinkedList();
//2. Put each point with 0 in degree into the queue as the starting node
for (int i = 0; i < inDegree.length; i++) {
if (inDegree[i] == 0) {
queue.add(i);
}
}
//Record the number of courses taken
int numChoose = 0;
//Record topology order
int[] topoOrder = new int[numCourses];
//3. Constantly take out a point from the queue, remove all connected edges of this point (edges pointing to other points), and the corresponding penetration of other points is - 1
while (!queue.isEmpty()) {
int nowPos = (int) queue.poll();
//Record courses taken
topoOrder[numChoose] = nowPos;
numChoose++;
//From this course to other courses, traverse and reduce the entry by one
for (int i = 0; i < graph[nowPos].size(); i++) {
int nextPos = (int) graph[nowPos].get(i);
//The neighbor's degree at the current point is reduced by one, which means that a prerequisite course for each subsequent course has been completed
inDegree[nextPos]--;
//4. Once a new point with a penetration of 0 is found, it will be thrown back into the queue
//Indicates that all the prerequisite courses of a later course have been completed and can be taken
if (inDegree[nextPos] == 0) {
queue.add(nextPos);
}
}
}
//If topological sorting is required, topoOrder can also be returned here
return (numChoose == numCourses) ? true : false;
}
}
Points worth learning:
- When defining pre courses and post courses, they are represented by a List. The pre courses are placed at the front and the post courses are placed at the back.
- In the definition of this graph, the List[] graph is ingeniously combined with the course subscript and array subscript.
4, BFS summary
- Those who can use BFS should not use DFS
- BFS usage scenarios
- Connected block problem
- Hierarchical traversal problem
- Topological sorting problem
- Whether level traversal is required
- One more loop is required, queue size()
- Matrix coordinate transformation array