preface
Most of this article is blind bb, and the big guys can choose not to read it.
You need to learn a little bit about linear algebra first.
Because I am too good, this blog will only discuss the two-dimensional situation.
Because I am too lazy, I will lack some schematic diagrams.
vector
Dot product / quantity product
Generally expressed by \ (\ vec a \cdot \vec b \), there are \ (\ vec a \cdot \vec b = | \ VEC a| \ VEC b| \ cos \ left < \ VEC a, \ VEC B \ right > = x_ax_b + y_ay_b \)
Where \ (\ left < \ vec a, \vec b \ right > \) represents the included angle of \ (\ vec a, \vec b \).
Simple application:
Judgment vector vertical: \ (\ vec a \bot \vec b \Longleftrightarrow \vec a\cdot \vec b = 0 \)
Judgment vector contribution: \ (\ VEC A / / \ VEC B \ longleftrightarrow \ VEC a \ cdot \ VEC B = | \ VEC a| \ VEC b| \)
Angle between judgment vectors: \ (\ cos \ left < \ VEC a, \ VEC B \ right > = \ frac {\ VEC a \ cdot \ VEC B} {\ VEC a | \ VEC B |} \)
Cross product
Very useful. It can be used to judge whether to rotate clockwise or counterclockwise from \ (\ vec a \) to \ (\ vec b \). At the same time, the absolute value of the cross product of the two vectors is equal to the area of the parallelogram sandwiched by the two vectors.
\(\ mathrm{PS} \): the cross product is actually a second-order determinant.
Next, we will abbreviate the cross product to \ (\ vec a\times \vec b \).
Cross product has distributive law and associative law (same as determinant).
The specific operations of cross product for judging rotation are as follows:
- Cross product \ (> 0 \), then rotate from \ (\ vec a \) to \ (\ vec b \), with the smallest rotation angle counterclockwise.
- Cross product \ (< 0 \), then rotate from \ (\ vec a \) to \ (\ vec b \), and the clockwise rotation angle is the smallest.
- Cross product (\ \ VEC), then \ VEC \ = 0.
In addition, the cross product can be used to determine which side of the line \ (l \) a point \ (P \) is on. Specifically, find two different points \ (A,B (A,B\in l) \) on the straight line, and then make the vector difference \ (\ vec a = A - B, \vec b = P - B \) to judge the positive and negative of \ (\ vec a\times \vec b \).
Polar coordinate system
Different from the ordinary two-dimensional rectangular coordinate system, we use the angle \ (\ theta \) (polar angle) and the distance from the origin (pole) \ (r \) (polar distance) to describe the position \ ((r \ theta) \) in a space. When converted to the normal rectangular coordinate system, it becomes \ ((r\cos \theta, r\sin \theta) \).
Polar coordinate system is convenient to describe some figures. For example, for the unit circle \ (C: x^2+y^2=1 \), it becomes a polar coordinate equation \ (r(\theta) = 1 \).
In order to convert the information of the plane rectangular coordinate system into the information of the polar coordinate system, we need to use a special trigonometric function: \ (\ mathrm{atan2} \), which has been built into the cmath of \ (\ rm C + + \).
\(\theta = \mathrm{atan2}(y,x), r = \frac{x}{\cos \theta}\).
basic operation
Rotate around a point
Given two points \ (P_1, P_2 \) and a rotation angle \ (\ theta \), find the point \ (P_3 \) obtained by rotating \ (\ theta \) clockwise around \ (P_2 \).
Here is the formula:
Find the intersection of lines
Give two points on two straight lines \ (l_1, l_2 \): \ (A,B,C,D (A,B\in l_1, C,D\in l_2) \) and find the intersection point \ (P (P = l_1\cap l_2) \).
Give a little picture:

Drawing Description: \ (AE//BD, DE//AB,CF//AB,EF//CD, AE\cap DE = E, EF\cap CF = F \).
Easily available:
Because \ ({\ text {quadrilateral} ABDE}, s {\ text {quadrilateral} CDEF} \) has the same bottom, the area ratio is equal to the height ratio, and then
Therefore, we can get:
Then you can get the coordinates of \ (P \):
convex hull
Relationship between judgment point and convex polygon
The cross product can be used to judge whether a point is in the convex hull.
Specifically, if you need to judge whether a point \ (P \) is in the convex hull, you can scan the convex hull counterclockwise. For each edge \ (a {I-1} a _i \), you need to meet \ ((P-A {I-1}) \ times \ overrightarrow {a {I-1} a_ i} \ge 0\) . This algorithm is obviously \ (O(\text {number of convex hull edges}) \), and needs to be optimized.
Algorithm 1
Make a straight line \ (y = y_P \), and the intersection of this line and the convex hull is \ (P_1, P_2 \) (when the intersection is less than one, it is obvious that \ (P \) is not in the convex hull). We can directly judge the size relationship between \ (x_P \) and \ (P_1, P_2 \). If and only if \ (x_{p_1} \ Leq x_P \ Leq x_2} \), \ (P \) is in the convex hull.
The bottleneck of the algorithm is obviously looking for the intersection, which I don't quite understand.
Algorithm 2
Using the cross product, let the sequence of points formed by the counterclockwise rotation of the convex polygon be \ (P_{1\dots m} \), then make \ (m-1 \) ray, in which the starting point of the \ (I \) ray \ (L_i \) is \ (P_1 \) and the direction is the direction of the vector \ (\ overrightarrow {p_1p {I + 1}} \). This operation is actually triangulating the polygon.
Obviously, when \ (P \) is to the right of \ (L_1 \) or to the left of \ (L_{m-1} \), then \ (P \) is not in the convex hull. Then, you can find out which two rays the point \ (P \) is sandwiched in by bisection. Assuming it is sandwiched between the rays \ (L_i, L_{i+1} \), use the cross product to judge whether the point is on the left side of \ (\ overrightarrow{P_{i+1}P_{i+2}} \) (or on the line segment where the vector is located). If so, then \ (P \) is in the convex polygon, otherwise it is not.
bool jdg_in_hull(Vector2* hl/*Convex polygons follow a counterclockwise sequence*/, int hl_sz, Vector2 p) {
if (cross(p - hl[1], hl[hl_sz] - hl[1]) < 0 || cross(p - hl[1], hl[2] - hl[1]) > 0) return false;
int l = 2, r = hl_sz - 1, bl = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (cross(hl[mid] - hl[1], p - hl[1]) > 0) bl = mid, l = mid + 1;
else r = mid - 1;
}
return cross(p - hl[bl], hl[bl + 1] - hl[bl]) <= 0;
}
Find convex hull
\Template questions for (\ Rightarrow \rm luogu \)
Given \ (n \) points on the plane, we choose to find some of them. The convex polygon surrounded by them can wrap these \ (n \) points (in / on the convex hull).
Algorithm 1: Andrew algorithm
Sort all points from small to large according to the abscissa as the first keyword and the ordinate as the second keyword. Maintain the convex shell with a stack. The maintenance condition can be that the cross product of adjacent points in the stack is positive. First scan all points in order to find the lower convex shell, and then start from the last point in the stack and scan the points in reverse order to get the upper convex shell, Then you can get the whole convex hull.
struct Vector2 {
LD x, y;
Vector2(LD x = 0, LD y = 0) : x(x), y(y) {}
} p[maxn], stk[maxn << 1];
int stk_tp;
inline Vector2 operator + (Vector2 a, Vector2 b) { return Vector2(a.x + b.x, a.y + b.y); }
inline Vector2 operator - (Vector2 a, Vector2 b) { return Vector2(a.x - b.x, a.y - b.y); }
inline bool operator < (Vector2 a, Vector2 b) {
return (a.x == b.x ? a.y < b.y : a.x < b.x);
}
inline LD len(Vector2 a) { return sqrt(a.x * a.x + a.y * a.y); }
inline LD cross(Vector2 a, Vector2 b) { return a.x * b.y - a.y * b.x; }
void find_hull() {
sort(p + 1, p + 1 + n);
stk[1] = p[1], stk[stk_tp = 2] = p[2];
for (int i = 3; i <= n; i++) {
while (stk_tp > 1 && cross(p[i] - stk[stk_tp - 1], stk[stk_tp] - stk[stk_tp - 1]) > 0)
stk_tp--;
stk[++stk_tp] = p[i];
}
stk[++stk_tp] = p[n - 1];
for (int i = n - 2; i >= 1; i--) {
while (stk_tp > 1 && cross(p[i] - stk[stk_tp - 1], stk[stk_tp] - stk[stk_tp - 1]) > 0)
stk_tp--;
stk[++stk_tp] = p[i];
}
//At this time, the point in the stack is the point where the convex hull rotates counterclockwise, and p[1] is calculated twice
}
Algorithm 2: Graham scanning method
Use polar coordinate system.
Find the smallest point according to the abscissa as the first keyword and the ordinate as the second keyword, then take this point as the pole, and then sort the remaining points according to the pole angle from small to large. Still use the stack to maintain the convex hull, and just scan it in sequence.
//This is written by big brother klii(tjp)
using namespace std;
const int N = 2e5 + 5;
struct Vec {
double x, y;
}p[N];
int n, stk[N], top;
Vec getvec(int a, int b) {
return (Vec){p[b].x - p[a].x, p[b].y - p[a].y};
}
double Cross(Vec a, Vec b) {
return a.x * b.y - a.y * b.x;
}
double dist(int a, int b) {
return sqrt((p[a].x - p[b].x) * (p[a].x - p[b].x) + (p[a].y - p[b].y) * (p[a].y - p[b].y));
}
bool cmp(Vec a, Vec b) {
if (a.x == p[1].x && b.x == p[1].x) return a.y < b.y;
double t1 = atan2(a.y - p[1].y, a.x - p[1].x);
double t2 = atan2(b.y - p[1].y, b.x - p[1].x);
return t1 == t2 ? a.x < b.x : t1 < t2;
}
int main() {
scanf("%d", &n);
int idx = 1;
for (int i = 1; i <= n; i++) {
scanf("%lf%lf", &p[i].x, &p[i].y);
if (p[i].y < p[idx].y || p[i].y == p[idx].y && p[i].x < p[idx].x) idx = i;
}
swap(p[1], p[idx]);
sort(p + 2, p + 1 + n, cmp);
stk[top = 1] = 1;
for (int i = 2; i <= n; i++) {
while (top > 1 && Cross(getvec(stk[top - 1], stk[top]), getvec(stk[top], i)) < 0) top--;
stk[++top] = i;
}
double ans = 0;
stk[top + 1] = stk[1];
for (int i = 1; i <= top; i++) ans += dist(stk[i], stk[i + 1]);
printf("%.2lf", ans);
return 0;
}
Rotating cartridge
The algorithm with various pronunciation can be used to find the diameter of the convex hull (the distance between the farthest two points in the convex hull).
\Template questions for (\ Rightarrow \rm luogu \)
You can think of a simple violence: first enumerate the edges on a convex hull, then find the point farthest from the edge, and then connect the two endpoints of the edge with that point to update the answer. The way to find the distance can be to find the area in determinant, and then remove the length of the edge.
The rotating cartridge is actually just to optimize the violence above. Consider the clockwise side \ (l \), assuming that the (i \) side is currently considered, and the farthest point is \ (p_j \), then consider the \ (i + 1 \) side. It is obvious that the farthest point will be the point reached by \ (p_j \) moving clockwise for a certain number of times instead of moving counterclockwise, which is obviously not good.
Considering the total number of clockwise moves, it can be found that the points on each convex hull will only pass through \ (O(1) \) times, so the total time complexity is obviously \ (O(n) \).
//PS: early code style
int operator * (Vector2 a, Vector2 b) {
return a.x * b.y - a.y * b.x;
}
LL dist(Vector2 a, Vector2 b) {
Vector2 c = a - b;
return c.x * c.x + c.y * c.y;
}
void find_hull() {
sort(a + 1, a + 1 + n);
stk[tp = 1] = a[1];
for (int i = 2; i <= n; i++) {
while (tp > 1 && (stk[tp] - stk[tp - 1]) * (a[i] - stk[tp - 1]) <= 0)
tp--;
stk[++tp] = a[i];
}
int tmp = tp;
for (int i = n - 1; i >= 1; i--) {
while (tp > tmp && (stk[tp] - stk[tp - 1]) * (a[i] - stk[tp - 1]) <= 0)
tp--;
stk[++tp] = a[i];
}
for (int i = 1; i <= tp; i++) p[i] = stk[i];
p_sz = tp - 1;
}
Vector2 cc;
LL diame;
void calc_diame() {
diame = 0;
if (p_sz == 2) {
cc = (p[1] + p[2]) / 2;
diame = dist(p[1], p[2]);
return ;
}
int to = 2;
for (int i = 1; i <= p_sz; i++) {
//move
while ((p[i+1]-p[i])*(p[to]-p[i]) < (p[i+1]-p[i])*(p[to+1]-p[i]))
to = to % p_sz + 1;
//Update answer
if (diame < dist(p[to], p[i])) {
diame = dist(p[to], p[i]);
cc = (p[to] + p[i]) / 2;
}
if (diame < dist(p[to], p[i+1])) {
diame = dist(p[to], p[i+1]);
cc = (p[to] + p[i+1]) / 2;
}
}
}
Example: P3187 [HNOI2007] minimum rectangular coverage
It is conceivable that one of the edges of the rectangle of the answer must be collinear with one of the edges on the convex hull.
Therefore, the height of the optimal rectangle corresponding to each edge \ (l \) can be obtained by rotating the cartridge. As for the width, it is obviously determined by the point with the smallest dot product composed of \ (l \) and the point with the largest dot product composed of \ (l \). Obviously, these two points can also be maintained in a similar way to rotating the cartridge.
void calc_ans() {
int j1 = 2, j2 = 2, j3 = 1;
stk_tp--;
for (int i = 1; i <= stk_tp; i++) {
while (cross(stk[j1 + 1] - stk[i], stk[i + 1] - stk[i]) >= cross(stk[j1] - stk[i], stk[i + 1] - stk[i]))
j1 = j1 % stk_tp + 1;
while (dot(stk[j2 + 1] - stk[i + 1], stk[i] - stk[i + 1]) <= dot(stk[j2] - stk[i + 1], stk[i] - stk[i + 1]))
j2 = j2 % stk_tp + 1;
if (i == 1) j3 = j1;
while (dot(stk[j3 + 1] - stk[i], stk[i + 1] - stk[i]) <= dot(stk[j3] - stk[i], stk[i + 1] - stk[i]))
j3 = j3 % stk_tp + 1;
LD len_i = len(stk[i + 1] - stk[i]);
LD l = dot(stk[j2] - stk[i], stk[i + 1] - stk[i]) / len_i,
r = dot(stk[j3] - stk[i + 1], stk[i] - stk[i + 1]) / len_i,
u = cross(stk[j1] - stk[i], stk[i + 1] - stk[i]) / len_i;
l = abs(l), r = abs(r), u = abs(u);
LD S = (l + r - len_i) * u;
if (S < ans) {
ans = S;
//PS: the point here is clockwise and should be output backwards
ap1 = stk[i + 1] - (r / len_i) * (stk[i + 1] - stk[i]),
ap2 = ap1 + ((l + r - len_i) / len_i) * (stk[i + 1] - stk[i]),
ap3 = ap2 + (u / len(stk[j2] - ap2)) * (stk[j2] - ap2),
ap4 = ap3 - ((l + r - len_i) / len_i) * (stk[i + 1] - stk[i]);
}
}
}
Half plane intersection
Half plane: given a line \ (l \) on the plane, the point set of all points above / below the line is called half plane, and half is defined as:
The \ (\ leq \) here can be replaced by \ (<, >, \ Ge \).
The two representations have their own advantages, and the second one is often used to find the and related information of multiple convex polygons.
\(\ Rightarrow \rm luogu \) template questions
Here, all half planes are set to the left of the line (i.e. the unequal sign is $\ ge $).
Here, find out all the straight lines first, and then sort them according to the polar angle from small to large. Here, using the polar angle instead of the slope can avoid discussing the non-existent slope.
Next, a double ended queue \ (\ rm deque \) is used to maintain the information.
Consider adding a new line \ (L \), in which the line at the end of the queue is \ (l_1 \), the line at the end of the queue is \ (l_2 \), and its intersection is \ (P \). If \ (P \) is on the right side of \ (L \), adding the intersection of the second half plane of \ (L \) is equivalent to adding \ (L \), and then deleting the intersection of \ (l_1 \), so you can pop up \ (l_1 \) directly (use the diagram of \ (\ rm dalao~klii \); If \ \ (L) cannot be rounded off (P \). (\ (l\rightarrow \text {red}, l_1\rightarrow \text {green}, l_2\rightarrow \text {blue} \))
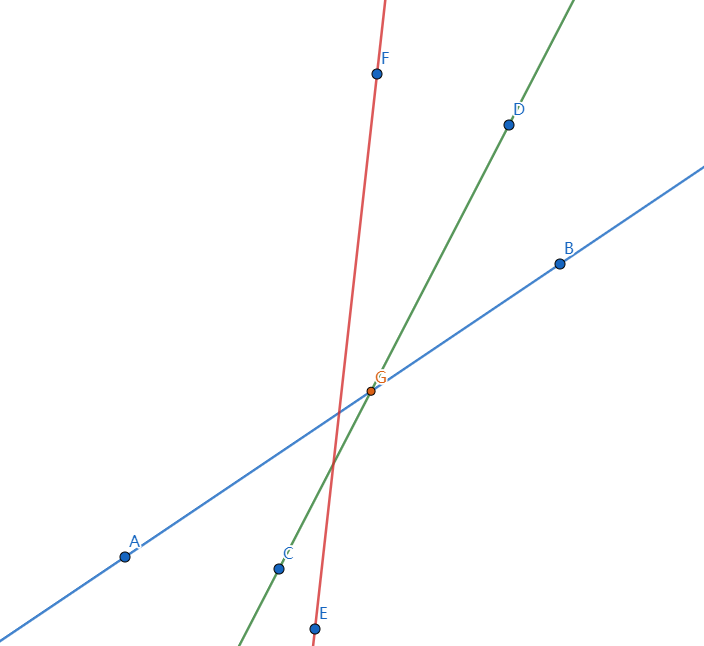
At the same time \ (l \) may also have an impact on the team leader: (\ (l\rightarrow \text {red}, \ text {team leader} \ rightarrow \text {green}, \ text {team leader next} \ rightarrow \text {blue} \))
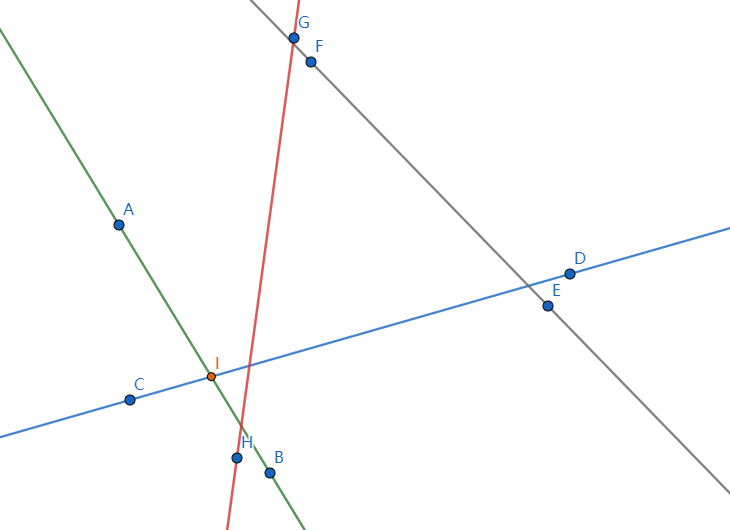
Therefore, when the intersection of the queue head is on the right side of \ (l \), the queue head also needs to pop up.
struct Line {
Vector2 a, b; LD k;
Line(Vector2 a = Vector2(0, 0), Vector2 b = Vector2(0, 0), LD k = 0) : a(a), b(b), k(k) {}
} l[maxn], tl[maxn];
inline LD get_slope(Vector2 a) { return atan2(a.y, a.x); }
bool cmp(Line a, Line b) {
return abs(a.k - b.k) > EPS ? a.k < b.k : cross(b.a - a.a, a.b - a.a) > EPS;
}
inline bool chk_right(Line a, Vector2 b) { return cross(b - a.a, a.b - a.a) > EPS; }
Vector2 its[maxn];
inline Vector2 get_intersect(Line a, Line b) {
return a.a + (cross(b.a - a.a, b.b - b.a) / cross(a.b - a.a, b.b - b.a)) * (a.b - a.a);
}
int q[maxn], ql, qr;
LD calc_intersect_S() {
sort(l + 1, l + 1 + m, cmp);
ql = 1, qr = 0; int cnt;
tl[cnt = 1] = l[1];
for (int i = 2; i <= m; i++) if (abs(l[i].k - l[i - 1].k) > EPS)
tl[++cnt] = l[i];
for (int i = 1; i <= cnt; i++) {
while (ql < qr && chk_right(tl[i], its[qr])) qr--;
while (ql < qr && chk_right(tl[i], its[ql + 1])) ql++;
q[++qr] = i;
if (ql < qr) its[qr] = get_intersect(tl[q[qr - 1]], tl[q[qr]]);
}
while (ql < qr && chk_right(tl[q[ql]], its[qr])) qr--;
its[ql] = get_intersect(tl[q[ql]], tl[q[qr]]);
LD res = 0;
for (int i = ql + 2; i <= qr; i++) res += cross(its[i - 1] - its[ql], its[i] - its[ql]);
return res / 2;
}
Vector2 pls[maxn];
int main() {
int n, mi; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &mi);
for (int j = 1; j <= mi; j++) scanf("%Lf %Lf", &pls[j].x, &pls[j].y);
pls[mi + 1] = pls[1];
for (int j = 1; j <= mi; j++)
l[++m] = Line(pls[j], pls[j + 1], get_slope(pls[j + 1] - pls[j]));
}
printf("%.3Lf\n", calc_intersect_S());
return 0;
}
Give a simple example: \(\ Rightarrow\) P3222 [HNOI2012] archery
Minkowski sum
Give a definition: let \ (A,B \) be two point sets, and its Minkowski sum is \ (A+B \). The operation rules are as follows:
It can be understood as follows: the point set obtained by offsetting each point in \ (B \) according to each point in \ (A \).
It seems that the time complexity of Minkowski sum of any two point sets can only be \ (O (|a|b|) \). However, if it is the convex hull of Minkowski sum, you can achieve \ (O(|A\text {convex hull number}| + |B\text {convex hull number}|) \).
Set the convex hull polygon of point set \ (A \) as \ (H(A) \).
First, find \ (H(A),H(B) \). Select the point \ (P_1, P_2 \) with the smallest coordinate in \ (H(A),H(B) \) (here, select the point with the smallest abscissa and the smallest ordinate). Then the point with the smallest coordinate in \ (H(A+B) \) is obviously \ (P_1+P_2 \).
Then, through drawing and finding the law, it can be found that all edges in \ (H(A+B) \) have appeared in \ (H(A),H(B) \), so the edges in \ (H(A),H(B) \) form a sequence counterclockwise, and then merge according to the polar angle from small to large to get \ (H(A+B) \).
int hl1_sz, hl2_sz, shl_sz;
struct Vector2 { ... } p1[maxn], p2[maxn], hl1[maxn], hl2[maxn], l[maxn], shl[maxn];
...
bool hull_cmp(Vector2 a, Vector2 b) { return a.x != b.x ? a.x < b.x : a.y < b.y; }
Vector2 t[maxn], t2[maxn]; int tsz;
void get_hull(Vector2* p, int n, Vector2* hl, int& cnt) {
sort(p + 1, p + 1 + n, hull_cmp), t[1] = p[1], t[tsz = 2] = p[2];
for (int i = 3; i <= n; i++) {
while (tsz > 1 && cross(p[i] - t[tsz - 1], t[tsz] - t[tsz - 1]) >= 0) tsz--;
t[++tsz] = p[i];
}
t[++tsz] = p[n - 1];
for (int i = n - 2; i >= 1; i--) {
while (tsz > 1 && cross(p[i] - t[tsz - 1], t[tsz] - t[tsz - 1]) >= 0) tsz--;
t[++tsz] = p[i];
}
cnt = tsz - 1;
for (int i = 1; i <= tsz; i++) hl[i] = t[i];
}
//There may be some repeated edges or points here. You need to make another convex hull of shl to get H(A+B)
void Minkowski(Vector2* hl1, Vector2* hl2, int hl1_sz, int hl2_sz, Vector2* shl, int& shl_sz) {
int p1 = 0, p2 = 0;
shl[shl_sz = 1] = hl1[1] + hl2[1];
for (int i = 1; i < hl1_sz; i++) t[i] = hl1[i + 1] - hl1[i];
for (int i = 1; i < hl2_sz; i++) t2[i] = hl2[i + 1] - hl2[i];
t[hl1_sz] = hl1[1] - hl1[hl1_sz], t2[hl2_sz] = hl2[1] - hl2[hl2_sz];
while (p1 < hl1_sz || p2 < hl2_sz) {
Vector2 cho;
if (p1 == hl1_sz) cho = t2[++p2];
else if (p2 == hl2_sz) cho = t[++p1];
else cho = (cross(t[p1 + 1], t2[p2 + 1]) >= 0 ? t[++p1] : t2[++p2]);
shl[shl_sz + 1] = cho + shl[shl_sz], ++shl_sz;
}
}
Minkowski(hl1, hl2, hl1_sz, hl2_sz, shl, shl_sz);
get_hull(shl, shl_sz, hl1, hl1_sz);
// hl1[1...hl1_sz] is the final convex hull
Examples
P4557 [JSOI2018] war
\(\ Rightarrow \rm luogu \) link
Given two point sets \ (A,B \), ask \ (Q \) times, give an offset vector \ ((dx, dy) \) each time, offset all vectors in \ (B \) according to this offset vector, and ask whether the convex hull of \ (A,B \) has intersection at this time.
It is conceivable that there is an intersection if and only if \ (\ exists a\in A\text {convex hull}, b\in B\text {convex hull}, b+(dx,dy) = a \), deforming it, we can get:
After transformation, we can get this proposition:
Here \ (- B \) refers to inverting all coordinates in \ (B \).
Here, we can find the convex hull of \ (A-B \) directly by Minkowski sum, and then judge whether \ ((dx,dy) \) is in the convex hull.