Source of learning materials: Zero basis introduction deep learning (3) - neural network and back propagation algorithm

I. neurons

Neurons and perceptrons are essentially the same, except that the activation function of neurons is sigmoid function and tanh function, as shown in the following figure:

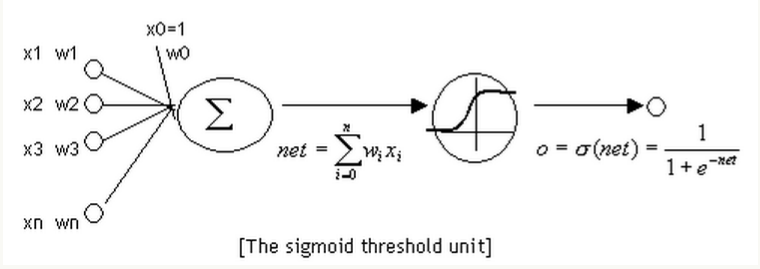
The sigmoid function is defined as follows:

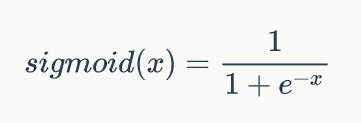
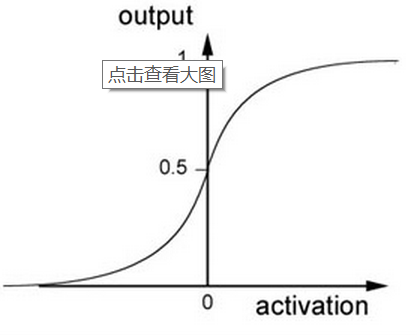
sigmoid function is a nonlinear function with a range of (0,1). The function image is shown in the following figure:

Meanwhile, the derivative of sigmoid function is:

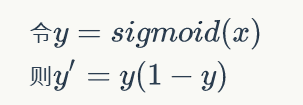
It can be seen that the derivative of sigmoid function is expressed by sigmoid function itself. Once the value of sigmoid function is calculated, it is very convenient to calculate the value of its derivative.

Assuming that the input of neuron is vector x, the weight vector is w, and the activation function is sigmoid function, its output y:

 

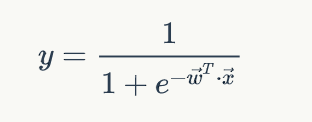
2, Neural network

2.1 definition of neural network

Neural network: multiple neurons connected according to certain rules.  

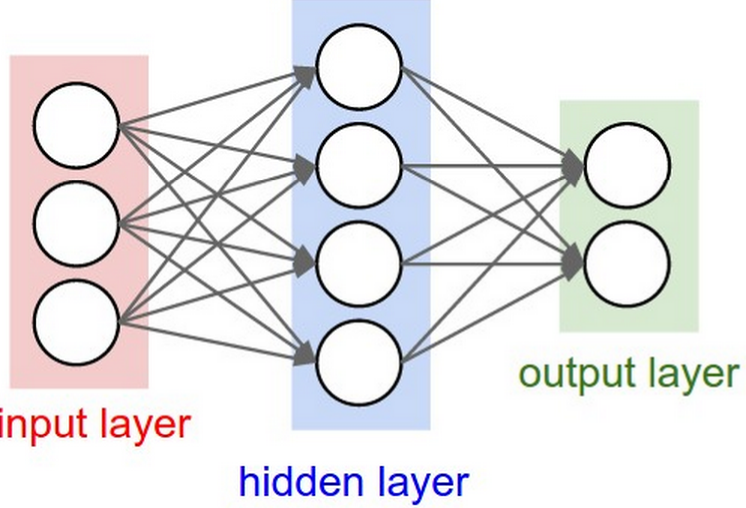
The fully connected (FC) neural network is shown in the figure below:

The rules are as follows:

• Neurons are arranged in layers. The leftmost layer is called the input layer (responsible for receiving input data); The rightmost layer is called the output layer (obtaining the output data of neural network); The layer between the input layer and the output layer is called a hidden layer (invisible to the outside).
• There is no connection between neurons in the same layer.
• Each neuron in layer N is fully connected to all neurons in layer N-1. The output of neurons in layer N-1 is the input of neurons in layer n.
• Each connection has a weight.

2.2 output calculation of neural network

Neural network is a function from input vector x to output vector y, namely:

To calculate the output of the neural network according to the input, first assign the value of each element xi of the input vector x to the corresponding neuron of the input layer of the neural network, and then calculate the value of each neuron of each layer according to y=sigmoid(wx+b) until the values of all neurons of the output layer of the last layer are calculated. Finally, the output vector y is obtained by concatenating the values of each neuron in the output layer.

2.3 training of neural network

Neural network is a model, and the weight (what the model needs to learn) is the parameter of the model. However, the connection mode of a neural network, the number of layers of the network and the number of nodes in each layer (not learned) are artificially set in advance. These artificially set parameters are called hyper parameters.

Training algorithm of neural network: Back Propagation algorithm

Suppose each training sample is (x,t), where vector x is the characteristic of the training sample and t is the target value of the sample.

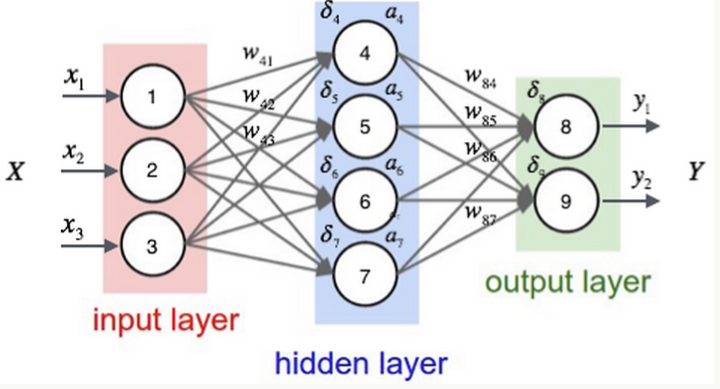
Firstly, according to the output calculation method of neural network, the output ai of each hidden layer node and the output yi of each node in the output layer are calculated by using the characteristic x of the sample.

Then, the error term of each node is calculated according to the following method δ i. Namely

• For output layer node i,

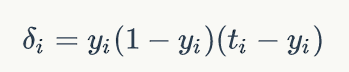
Among them, δ I is the error term of node i, yi is the output value of node i, and ti is the target value of the sample corresponding to node I.

• For hidden layer nodes i,

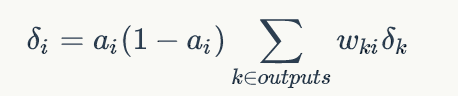
Where ai is the output value of node i and wki is the weight of the connection from node i to its next layer node k, δ k is the error term of node k next to node I.

Finally, update the weights on each connection:

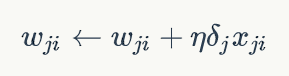
Where wji is the weight from node i to node j, η Is the learning rate, δ J is the error term of node j, and xji is the input passed from node i to node j.

It can be seen that to calculate the error term of each node, you need to calculate the error term of the next layer node connected to each node. This requires that the calculation order of the error term must start from the output layer, and then calculate the error term of each hidden layer in reverse order until the hidden layer connected to the input layer. This is the meaning of the name of the back propagation algorithm. When the error terms of all nodes are calculated, we can update all weights.

Therefore, the derived training rules are based on the fact that the activation function is sigmoid function, the objective function is square sum error, the neural network is fully connected network, and the optimization algorithm is random gradient descent optimization algorithm. If the activation function, error calculation method, network connection structure and optimization algorithm are different, the specific training rules will be different.

2.4 realization of neural network

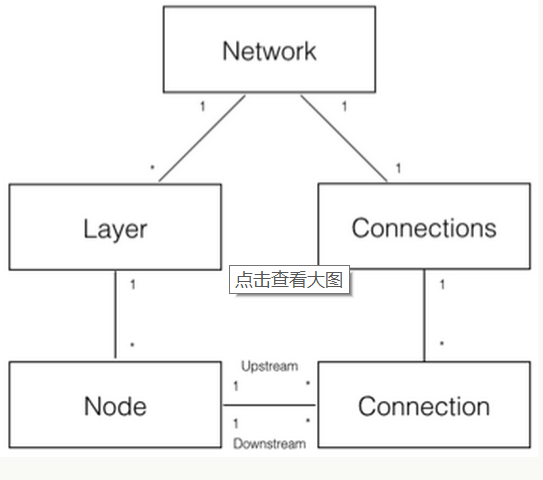
First, make a basic model and decompose five domain objects to realize the neural network:

• Network neural network object, which provides API interface. It consists of several layer objects and connected objects.
• Layer layer, consisting of multiple nodes.
• The Node object calculates and records the information of the Node itself (such as output value a and error term) δ And the upstream and downstream connections associated with this Node.
• Connection each connection object should record the weight of the connection.
• Connections only serves as the collection object of Connection and provides some collection operations.

# Node implementation
# The node class is responsible for recording and maintaining the node's own information and the upstream and downstream connections related to this node, and realizing the calculation of output value and error term.
class Node(object):
    def __init__(self, layer_index, node_index):
        '''
        Construct node objects.
        layer_index: The number of the layer to which the node belongs
        node_index: Node number
        '''
        self.layer_index = layer_index
        self.node_index = node_index
        self.downstream = []
        self.upstream = []
        self.output = 0
        self.delta = 0
    def set_output(self, output):
        '''
        Sets the output value of the node. This function is used if the node belongs to the input layer.
        '''
        self.output = output
    def append_downstream_connection(self, conn):
        '''
        Add a connection to the downstream node
        '''
        self.downstream.append(conn)
    def append_upstream_connection(self, conn):
        '''
        Add a connection to the upstream node
        '''
        self.upstream.append(conn)
    def calc_output(self):
        '''
        Calculate the output of the node according to equation 1
        '''
        output = reduce(lambda ret, conn: ret + conn.upstream_node.output * conn.weight, self.upstream, 0)
        self.output = sigmoid(output)
    def calc_hidden_layer_delta(self):
        '''
        When the node belongs to the hidden layer, it is calculated according to equation 4 delta
        '''
        downstream_delta = reduce(
            lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
            self.downstream, 0.0)
        self.delta = self.output * (1 - self.output) * downstream_delta
    def calc_output_layer_delta(self, label):
        '''
        When the node belongs to the output layer, it is calculated according to equation 3 delta
        '''
        self.delta = self.output * (1 - self.output) * (label - self.output)
    def __str__(self):
        '''
        Print node information
        '''
        node_str = '%u-%u: output: %f delta: %f' % (self.layer_index, self.node_index, self.output, self.delta)
        downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
        upstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.upstream, '')
        return node_str + '\n\tdownstream:' + downstream_str + '\n\tupstream:' + upstream_str 


# ConstNode object
class ConstNode(object):
    def __init__(self, layer_index, node_index):
        '''
        Construct node objects.
        layer_index: The number of the layer to which the node belongs
        node_index: Node number
        '''    
        self.layer_index = layer_index
        self.node_index = node_index
        self.downstream = []
        self.output = 1
    def append_downstream_connection(self, conn):
        '''
        Add a connection to the downstream node
        '''       
        self.downstream.append(conn)
    def calc_hidden_layer_delta(self):
        '''
        When the node belongs to the hidden layer, it is calculated according to equation 4 delta
        '''
        downstream_delta = reduce(
            lambda ret, conn: ret + conn.downstream_node.delta * conn.weight,
            self.downstream, 0.0)
        self.delta = self.output * (1 - self.output) * downstream_delta
    def __str__(self):
        '''
        Print node information
        '''
        node_str = '%u-%u: output: 1' % (self.layer_index, self.node_index)
        downstream_str = reduce(lambda ret, conn: ret + '\n\t' + str(conn), self.downstream, '')
        return node_str + '\n\tdownstream:' + downstream_str


# Layer object
class Layer(object):
    def __init__(self, layer_index, node_count):
        '''
        Initialize layer 1
        layer_index: Layer number
        node_count: Number of nodes contained in the layer
        '''
        self.layer_index = layer_index
        self.nodes = []
        for i in range(node_count):
            self.nodes.append(Node(layer_index, i))
        self.nodes.append(ConstNode(layer_index, node_count))
    def set_output(self, data):
        '''
        Sets the output of the layer. Used when the layer is an input layer.
        '''
        for i in range(len(data)):
            self.nodes[i].set_output(data[i])
    def calc_output(self):
        '''
        Calculate the output vector of the layer
        '''
        for node in self.nodes[:-1]:
            node.calc_output()
    def dump(self):
        '''
        Print layer information
        '''
        for node in self.nodes:
            print node


# Connection object
class Connection(object):
    def __init__(self, upstream_node, downstream_node):
        '''
        Initialize the connection. The weight is initialized to a small random number
        upstream_node: Connected upstream node
        downstream_node: Connected downstream nodes
        '''
        self.upstream_node = upstream_node
        self.downstream_node = downstream_node
        self.weight = random.uniform(-0.1, 0.1)
        self.gradient = 0.0
    def calc_gradient(self):
        '''
        Calculated gradient
        '''
        self.gradient = self.downstream_node.delta * self.upstream_node.output
    def get_gradient(self):
        '''
        Gets the current gradient
        '''
        return self.gradient
    def update_weight(self, rate):
        '''
        Update the weight according to the gradient descent algorithm
        '''
        self.calc_gradient()
        self.weight += rate * self.gradient
    def __str__(self):
        '''
        Print connection information
        '''
        return '(%u-%u) -> (%u-%u) = %f' % (
            self.upstream_node.layer_index, 
            self.upstream_node.node_index,
            self.downstream_node.layer_index, 
            self.downstream_node.node_index, 
            self.weight)


# Connections object
class Connections(object):
    def __init__(self):
        self.connections = []
    def add_connection(self, connection):
        self.connections.append(connection)
    def dump(self):
        for conn in self.connections:
            print conn


#Network object
class Network(object):
    def __init__(self, layers):
        '''
        Initialize a fully connected neural network
        layers: A two-dimensional array describing the number of nodes in each layer of the neural network
        '''
        self.connections = Connections()
        self.layers = []
        layer_count = len(layers)
        node_count = 0;
        for i in range(layer_count):
            self.layers.append(Layer(i, layers[i]))
        for layer in range(layer_count - 1):
            connections = [Connection(upstream_node, downstream_node) 
                           for upstream_node in self.layers[layer].nodes
                           for downstream_node in self.layers[layer + 1].nodes[:-1]]
            for conn in connections:
                self.connections.add_connection(conn)
                conn.downstream_node.append_upstream_connection(conn)
                conn.upstream_node.append_downstream_connection(conn)
    def train(self, labels, data_set, rate, iteration):
        '''
        Training neural network
        labels: Array, training sample label. Each element is a label of a sample.
        data_set: Two dimensional array, training sample features. Each element is a feature of a sample.
        '''
        for i in range(iteration):
            for d in range(len(data_set)):
                self.train_one_sample(labels[d], data_set[d], rate)
    def train_one_sample(self, label, sample, rate):
        '''
        The internal function uses a sample to train the network
        '''
        self.predict(sample)
        self.calc_delta(label)
        self.update_weight(rate)
    def calc_delta(self, label):
        '''
        Internal function to calculate the of each node delta
        '''
        output_nodes = self.layers[-1].nodes
        for i in range(len(label)):
            output_nodes[i].calc_output_layer_delta(label[i])
        for layer in self.layers[-2::-1]:
            for node in layer.nodes:
                node.calc_hidden_layer_delta()
    def update_weight(self, rate):
        '''
        Internal function to update the weight of each connection
        '''
        for layer in self.layers[:-1]:
            for node in layer.nodes:
                for conn in node.downstream:
                    conn.update_weight(rate)
    def calc_gradient(self):
        '''
        Internal function to calculate the gradient of each connection
        '''
        for layer in self.layers[:-1]:
            for node in layer.nodes:
                for conn in node.downstream:
                    conn.calc_gradient()
    def get_gradient(self, label, sample):
        '''
        Obtain the gradient on each connection of the network under one sample
        label: Sample label
        sample: Sample input
        '''
        self.predict(sample)
        self.calc_delta(label)
        self.calc_gradient()
    def predict(self, sample):
        '''
        Predict the output value according to the input sample
        sample: Array, the characteristics of the sample, that is, the input vector of the network
        '''
        self.layers[0].set_output(sample)
        for i in range(1, len(self.layers)):
            self.layers[i].calc_output()
        return map(lambda node: node.output, self.layers[-1].nodes[:-1])
    def dump(self):
        '''
        Print network information
        '''
        for layer in self.layers:
            layer.dump()