This article will focus on some common skills in the process of machine learning training with Python. Mastering them can make you get twice the result with half the effort.
Most of the code used will be based on the last example in the previous article, which is to predict wages according to the conditions of farmers A kind of , if you haven't read the previous one, please click Here see.
Save and read model state
In pytorch, all kinds of operations are around the sensor object, and the parameters of the model are also the sensor. If we save the trained sensor to the hard disk and then read it from the hard disk next time, we can use it directly.
Let's first see how to save a single sensor. The following code runs in REPL of python:
# Reference pytorch >>> import torch # Create a new sensor object >>> a = torch.tensor([1, 2, 3], dtype=torch.float) # Save sensor to file 1.pt >>> torch.save(a, "1.pt") # Read sensor from file 1.pt >>> b = torch.load("1.pt") >>> b tensor([1., 2., 3.])
Store.save uses the pickle format of python when saving the sensor. This format ensures compatibility between different python versions, but does not support compression of content. Therefore, if the saved file of the sensor is very large, it will take up a lot of space. We can compress it before saving and decompress it before reading to reduce the file size:
# Reference compression library >>> import gzip # Save the sensor to the file 1.pt, and compress it with gzip >>> torch.save(a, gzip.GzipFile("1.pt.gz", "wb")) # Read the sensor from the file 1.pt and extract it with gzip >>> b = torch.load(gzip.GzipFile("1.pt.gz", "rb")) >>> b tensor([1., 2., 3.])
Torch.save not only supports saving a single sensor object, but also supports saving the list or dictionary of sensors (in fact, it can also save python objects other than sensors, as long as the pickle format is supported). We can call state Qu dict to get a set containing all parameters of the model, and then use torch.save to save the state of the model:
>>> from torch import nn >>> class MyModel(nn.Module): ... def __init__(self): ... super().__init__() ... self.layer1 = nn.Linear(in_features=8, out_features=100) ... self.layer2 = nn.Linear(in_features=100, out_features=50) ... self.layer3 = nn.Linear(in_features=50, out_features=1) ... def forward(self, x): ... hidden1 = nn.functional.relu(self.layer1(x)) ... hidden2 = nn.functional.relu(self.layer2(hidden1)) ... y = self.layer3(hidden2) ... return y ... >>> model = MyModel() >>> model.state_dict() OrderedDict([('layer1.weight', tensor([[ 0.2261, 0.2008, 0.0833, -0.2020, -0.0674, 0.2717, -0.0076, 0.1984], //Omit in transit output 0.1347, 0.1356]])), ('layer3.bias', tensor([0.0769]))]) >>> torch.save(model.state_dict(), gzip.GzipFile("model.pt.gz", "wb"))
You can use the load state dict function to read the model state, but you need to make sure that the parameter definition of the model does not change, otherwise the reading will make an error:
>>> new_model = MyModel() >>> new_model.load_state_dict(torch.load(gzip.GzipFile("model.pt.gz", "rb"))) <All keys matched successfully>
An important detail is that if you are not ready to continue training after reading the model state, but to predict other data, you should call the eval function to disable automatic differentiation and other functions, so as to speed up the operation:
>>> new_model.eval()
pytorch not only supports saving and reading the model state, but also supports saving and reading the whole model including code and parameters. However, I do not recommend this approach, because you will not see the model definition when you use it, and the class libraries or functions that the model depends on will not be saved together, so you still have to load them in advance, or you will make an error:
>>> torch.save(model, gzip.GzipFile("model.pt.gz", "wb")) >>> new_model = torch.load(gzip.GzipFile("model.pt.gz", "rb"))
Record the change of accuracy of training set and verification set
In the training process, we can record the change of the accuracy of the training set and the verification set to see whether it can converge, how fast the training is, and whether there has been a fitting problem. The following is a code example:
# References to pytorch and pandas and matchlib used to display charts import pandas import torch from torch import nn from matplotlib import pyplot # Define model class MyModel(nn.Module): def __init__(self): super().__init__() self.layer1 = nn.Linear(in_features=8, out_features=100) self.layer2 = nn.Linear(in_features=100, out_features=50) self.layer3 = nn.Linear(in_features=50, out_features=1) def forward(self, x): hidden1 = nn.functional.relu(self.layer1(x)) hidden2 = nn.functional.relu(self.layer2(hidden1)) y = self.layer3(hidden2) return y # Assign an initial value to the random number generator so that the same random number can be generated for each run # This is to make the training process repeatable, or you can choose not to torch.random.manual_seed(0) # Create model instance model = MyModel() # Create loss calculator loss_function = torch.nn.MSELoss() # Create parameter adjuster optimizer = torch.optim.SGD(model.parameters(), lr=0.0000001) # Read the original data set from csv df = pandas.read_csv('salary.csv') dataset_tensor = torch.tensor(df.values, dtype=torch.float) # Segmentation training set (60%), verification set (20%) and test set (20%) random_indices = torch.randperm(dataset_tensor.shape[0]) traning_indices = random_indices[:int(len(random_indices)*0.6)] validating_indices = random_indices[int(len(random_indices)*0.6):int(len(random_indices)*0.8):] testing_indices = random_indices[int(len(random_indices)*0.8):] traning_set_x = dataset_tensor[traning_indices][:,:-1] traning_set_y = dataset_tensor[traning_indices][:,-1:] validating_set_x = dataset_tensor[validating_indices][:,:-1] validating_set_y = dataset_tensor[validating_indices][:,-1:] testing_set_x = dataset_tensor[testing_indices][:,:-1] testing_set_y = dataset_tensor[testing_indices][:,-1:] # Record the change of accuracy of training set and verification set traning_accuracy_history = [] validating_accuracy_history = [] # Start the training process for epoch in range(1, 500): print(f"epoch: {epoch}") # Train and modify parameters according to training set # Switching the model to training mode will enable automatic differentiation, batchnorm and Dropout model.train() traning_accuracy_list = [] for batch in range(0, traning_set_x.shape[0], 100): # Only 100 sets of data can be calculated at a time batch_x = traning_set_x[batch:batch+100] batch_y = traning_set_y[batch:batch+100] # Calculate forecast predicted = model(batch_x) # Calculate loss loss = loss_function(predicted, batch_y) # Derivation function value from loss automatic differentiation loss.backward() # Adjust parameters with parameter adjuster optimizer.step() # Clear the value of the function optimizer.zero_grad() # Record the correct rate of this batch. Torch.no-grad means to temporarily disable the automatic differentiation function with torch.no_grad(): traning_accuracy_list.append(1 - ((batch_y - predicted).abs() / batch_y).mean().item()) traning_accuracy = sum(traning_accuracy_list) / len(traning_accuracy_list) traning_accuracy_history.append(traning_accuracy) print(f"training accuracy: {traning_accuracy}") # Check validation set # Switching the model to validation mode will disable automatic differentiation, batchnorm and Dropout model.eval() predicted = model(validating_set_x) validating_accuracy = 1 - ((validating_set_y - predicted).abs() / validating_set_y).mean() validating_accuracy_history.append(validating_accuracy.item()) print(f"validating x: {validating_set_x}, y: {validating_set_y}, predicted: {predicted}") print(f"validating accuracy: {validating_accuracy}") # Check test set predicted = model(testing_set_x) testing_accuracy = 1 - ((testing_set_y - predicted).abs() / testing_set_y).mean() print(f"testing x: {testing_set_x}, y: {testing_set_y}, predicted: {predicted}") print(f"testing accuracy: {testing_accuracy}") # Display the change of accuracy of training set and verification set pyplot.plot(traning_accuracy_history, label="traning") pyplot.plot(validating_accuracy_history, label="validing") pyplot.ylim(0, 1) pyplot.legend() pyplot.show() # Manual input data forecast output while True: try: print("enter input:") r = list(map(float, input().split(","))) x = torch.tensor(r).view(1, len(r)) print(model(x)[0,0].item()) except Exception as e: print("error:", e)
After 500 rounds of training, the following chart will be generated:
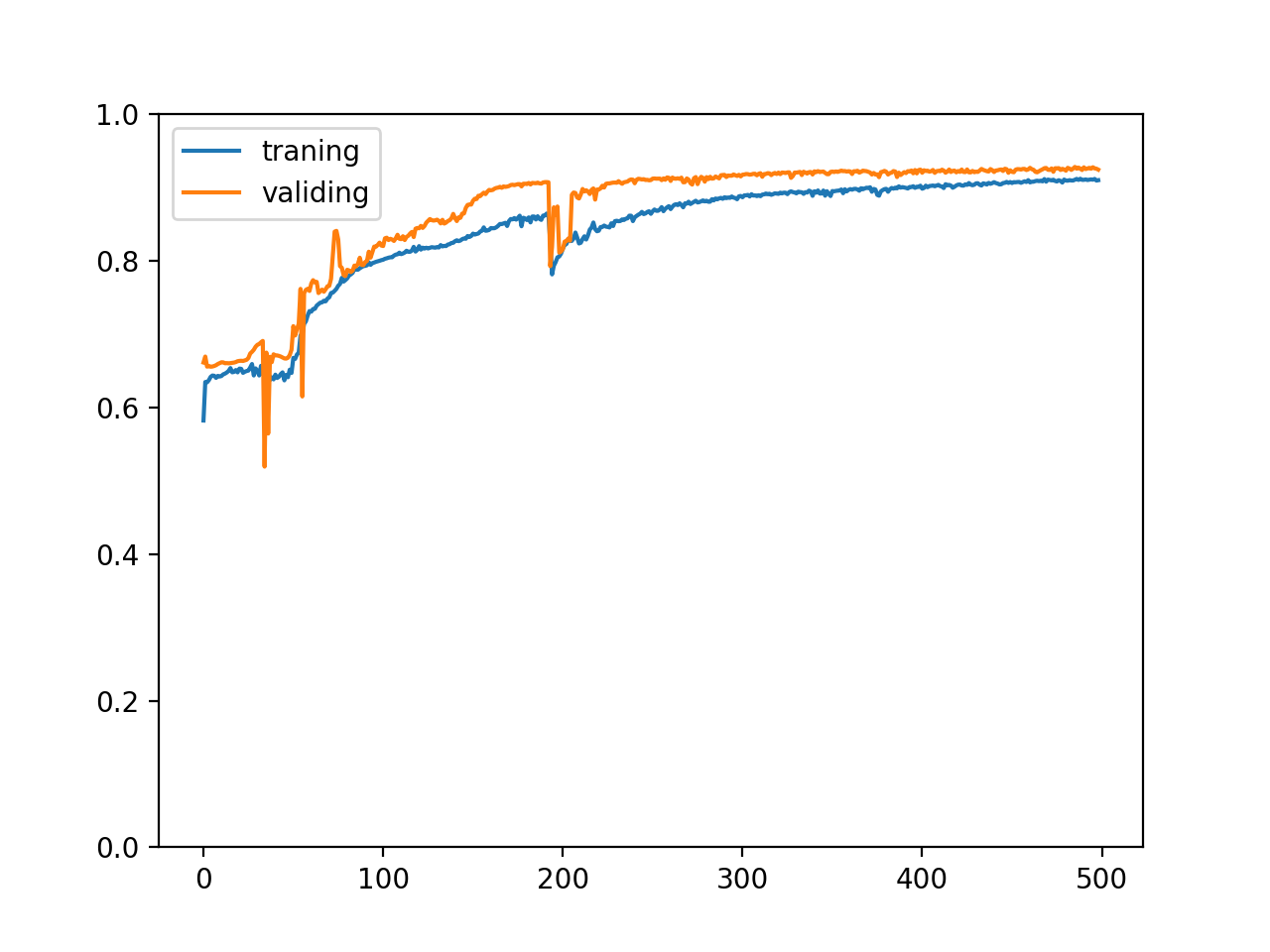
We can see from the chart that the correct rates of training set and verification set increase gradually with the training, and the two correct rates are very close, which means that the training is very successful. The model has mastered the rules for the training set and can successfully predict the untrained verification set, but in fact, we can hardly see such a chart, because the data set in the example is carefully constructed And generate enough data.
We may also see the following types of charts that represent different situations:
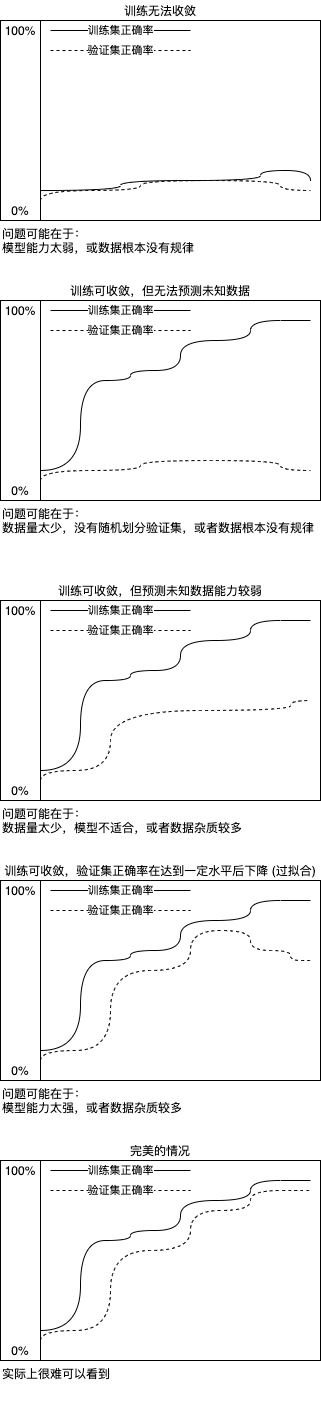
If there is enough data, the data obeys a certain rule and has less impurities, the training set and verification set can be divided evenly, and the appropriate model can be used to achieve the ideal situation, but it is difficult to achieve it in practice 😩. By analyzing the accuracy changes of training set and verification set, we can locate where the problem occurs, and the over fitting problem can be solved by early stopping (mentioned in the first article). Next, we will see how to decide when to stop the training.
Decide when to stop training
Do you remember the training process mentioned in the first article? We will learn how to implement this training process in the code:
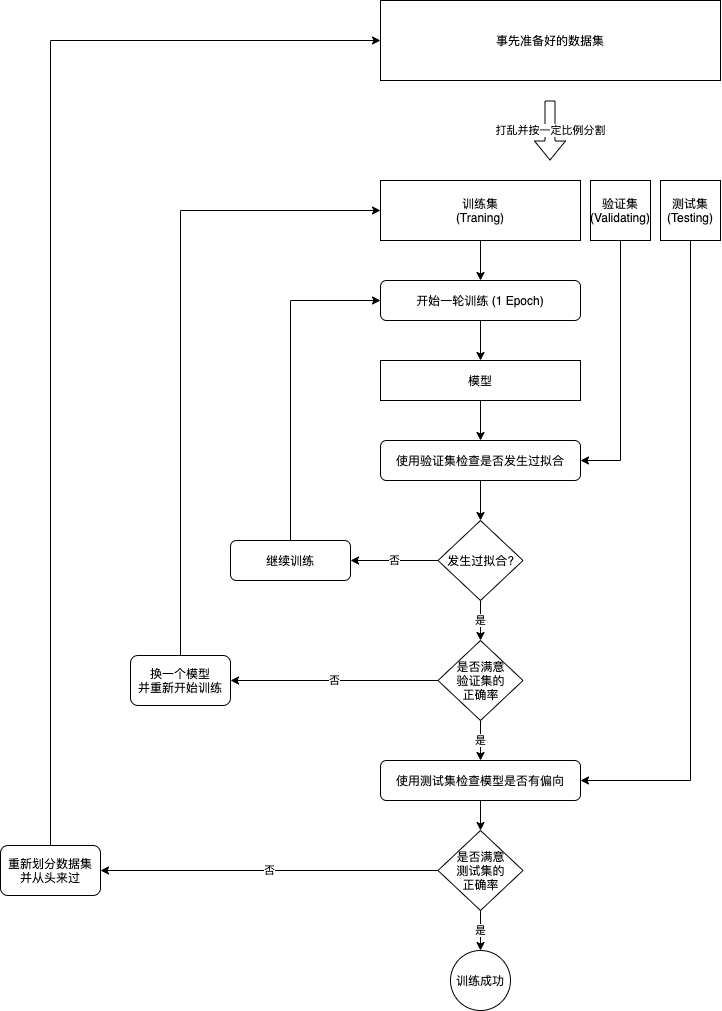
To judge whether the fitting has happened, we can simply record the highest verification set accuracy in history. If the highest accuracy has not been refreshed after many times of training, the training will end. At the same time of recording the highest accuracy, we need to save the state of the model. At this time, the model has found enough rules, but the parameters have not been modified to adapt to the impurities in the training set, which can achieve the best effect to predict the unknown data. This technique, also known as early stopping, is very common in machine learning.
The code implementation is as follows:
# References to pytorch and pandas and matchlib used to display charts import pandas import torch from torch import nn from matplotlib import pyplot # Define model class MyModel(nn.Module): def __init__(self): super().__init__() self.layer1 = nn.Linear(in_features=8, out_features=100) self.layer2 = nn.Linear(in_features=100, out_features=50) self.layer3 = nn.Linear(in_features=50, out_features=1) def forward(self, x): hidden1 = nn.functional.relu(self.layer1(x)) hidden2 = nn.functional.relu(self.layer2(hidden1)) y = self.layer3(hidden2) return y # Assign an initial value to the random number generator so that the same random number can be generated for each run # This is to make the training process repeatable, or you can choose not to torch.random.manual_seed(0) # Create model instance model = MyModel() # Create loss calculator loss_function = torch.nn.MSELoss() # Create parameter adjuster optimizer = torch.optim.SGD(model.parameters(), lr=0.0000001) # Read the original data set from csv df = pandas.read_csv('salary.csv') dataset_tensor = torch.tensor(df.values, dtype=torch.float) # Segmentation training set (60%), verification set (20%) and test set (20%) random_indices = torch.randperm(dataset_tensor.shape[0]) traning_indices = random_indices[:int(len(random_indices)*0.6)] validating_indices = random_indices[int(len(random_indices)*0.6):int(len(random_indices)*0.8):] testing_indices = random_indices[int(len(random_indices)*0.8):] traning_set_x = dataset_tensor[traning_indices][:,:-1] traning_set_y = dataset_tensor[traning_indices][:,-1:] validating_set_x = dataset_tensor[validating_indices][:,:-1] validating_set_y = dataset_tensor[validating_indices][:,-1:] testing_set_x = dataset_tensor[testing_indices][:,:-1] testing_set_y = dataset_tensor[testing_indices][:,-1:] # Record the change of accuracy of training set and verification set traning_accuracy_history = [] validating_accuracy_history = [] # Record the highest verification set accuracy validating_accuracy_highest = 0 validating_accuracy_highest_epoch = 0 # Start the training process for epoch in range(1, 10000): print(f"epoch: {epoch}") # Train and modify parameters according to training set # Switching the model to training mode will enable automatic differentiation, batchnorm and Dropout model.train() traning_accuracy_list = [] for batch in range(0, traning_set_x.shape[0], 100): # Only 100 sets of data can be calculated at a time batch_x = traning_set_x[batch:batch+100] batch_y = traning_set_y[batch:batch+100] # Calculate forecast predicted = model(batch_x) # Calculate loss loss = loss_function(predicted, batch_y) # Derivation function value from loss automatic differentiation loss.backward() # Adjust parameters with parameter adjuster optimizer.step() # Clear the value of the function optimizer.zero_grad() # Record the correct rate of this batch. Torch.no-grad means to temporarily disable the automatic differentiation function with torch.no_grad(): traning_accuracy_list.append(1 - ((batch_y - predicted).abs() / batch_y).mean().item()) traning_accuracy = sum(traning_accuracy_list) / len(traning_accuracy_list) traning_accuracy_history.append(traning_accuracy) print(f"training accuracy: {traning_accuracy}") # Check validation set # Switching the model to validation mode will disable automatic differentiation, batchnorm and Dropout model.eval() predicted = model(validating_set_x) validating_accuracy = 1 - ((validating_set_y - predicted).abs() / validating_set_y).mean() validating_accuracy_history.append(validating_accuracy.item()) print(f"validating x: {validating_set_x}, y: {validating_set_y}, predicted: {predicted}") print(f"validating accuracy: {validating_accuracy}") # Record the highest verification set accuracy and the current model state, and judge whether the record has not been refreshed after 100 trainings if validating_accuracy > validating_accuracy_highest: validating_accuracy_highest = validating_accuracy validating_accuracy_highest_epoch = epoch torch.save(model.state_dict(), "model.pt") print("highest validating accuracy updated") elif epoch - validating_accuracy_highest_epoch > 100: # After 100 times of training, I still haven't refreshed the record. End the training print("stop training because highest validating accuracy not updated in 100 epoches") break # Use the model state at the highest accuracy print(f"highest validating accuracy: {validating_accuracy_highest}", f"from epoch {validating_accuracy_highest_epoch}") model.load_state_dict(torch.load("model.pt")) # Check test set predicted = model(testing_set_x) testing_accuracy = 1 - ((testing_set_y - predicted).abs() / testing_set_y).mean() print(f"testing x: {testing_set_x}, y: {testing_set_y}, predicted: {predicted}") print(f"testing accuracy: {testing_accuracy}") # Display the change of accuracy of training set and verification set pyplot.plot(traning_accuracy_history, label="traning") pyplot.plot(validating_accuracy_history, label="validing") pyplot.ylim(0, 1) pyplot.legend() pyplot.show() # Manual input data forecast output while True: try: print("enter input:") r = list(map(float, input().split(","))) x = torch.tensor(r).view(1, len(r)) print(model(x)[0,0].item()) except Exception as e: print("error:", e)
The final output is as follows:
Omit starting output stop training because highest validating accuracy not updated in 100 epoches highest validating accuracy: 0.93173748254776 from epoch 645 testing x: tensor([[48., 1., 18., ..., 5., 0., 5.], [22., 1., 2., ..., 2., 1., 2.], [24., 0., 1., ..., 3., 2., 0.], ..., [24., 0., 4., ..., 0., 1., 1.], [39., 0., 0., ..., 0., 5., 5.], [36., 0., 5., ..., 3., 0., 3.]]), y: tensor([[14000.], [10500.], [13000.], ..., [15500.], [12000.], [19000.]]), predicted: tensor([[15612.1895], [10705.9873], [12577.7988], ..., [16281.9277], [10780.5996], [19780.3281]], grad_fn=<AddmmBackward>) testing accuracy: 0.9330222606658936
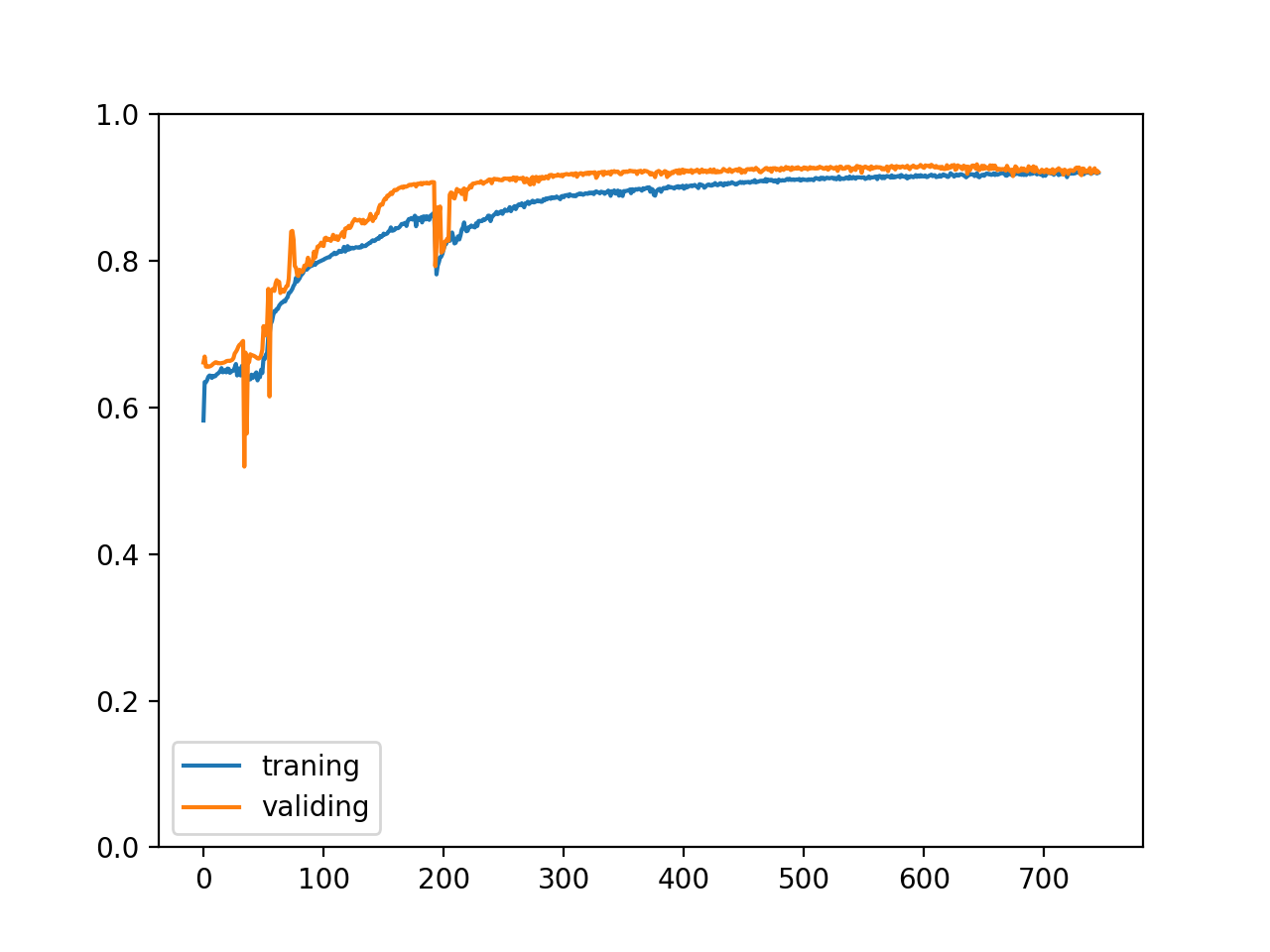
The correct rate of training set and verification set changes as follows, we can see that we are in a good place A kind of , there will be no improvement if we continue to train:
Improve program structure
We can also improve the program structure as follows:
- The process of separating preparation data sets from training
- Reading data in batches during training
- Provide a trained model for interface use
The training codes we have seen so far are all written in a program to prepare data sets, train, evaluate and use after training, which is easy to understand but will waste time in actual business. If you find a model is not suitable and need to modify the model, you have to start from scratch. We can separate the process of data set preparation and training, first read the original data and convert it to the sensor object, then save it to the hard disk, and then read the sensor object from the hard disk for training, so that if we need to modify the model but do not need to modify the input-output conversion to the sensor code, we can save the first step.
In the actual business, the data may be very large, so we can't read all the data into the memory and then divide them into batches. At this time, we can read the original data and transfer it to the sensor object in batches, and then read them from the hard disk one by one during the training process, so as to prevent the problem of insufficient memory.
Finally, we can provide an external interface to use the trained model. If your program is written by python, you can call it directly. However, if your program is written in other languages, you may need to establish a python server to provide REST services, or use TorchScript for cross language interaction. For details, please refer to the official Course.
In summary, we will split the following processes:
- Read the original data set and convert to the sensor object
- Save the sensor object to hard disk in batches
- Read and train the sensor object from the hard disk in batches
- Save the model state to the hard disk during training (generally select to save the model state when the accuracy of verification set is the highest)
- Provide a trained model for interface use
Here is the improved example code:
import os import sys import pandas import torch import gzip import itertools from torch import nn from matplotlib import pyplot class MyModel(nn.Module): """A model for forecasting wages based on the condition of farmers""" def __init__(self): super().__init__() self.layer1 = nn.Linear(in_features=8, out_features=100) self.layer2 = nn.Linear(in_features=100, out_features=50) self.layer3 = nn.Linear(in_features=50, out_features=1) def forward(self, x): hidden1 = nn.functional.relu(self.layer1(x)) hidden2 = nn.functional.relu(self.layer2(hidden1)) y = self.layer3(hidden2) return y def save_tensor(tensor, path): """Preservation tensor Object to file""" torch.save(tensor, gzip.GzipFile(path, "wb")) def load_tensor(path): """Read from file tensor object""" return torch.load(gzip.GzipFile(path, "rb")) def prepare(): """Prepare for training""" # The dataset will be saved in the data folder after it is converted to the sensor if not os.path.isdir("data"): os.makedirs("data") # Read the original data set from csv, 2000 lines at a time in batches for batch, df in enumerate(pandas.read_csv('salary.csv', chunksize=2000)): dataset_tensor = torch.tensor(df.values, dtype=torch.float) # Segmentation training set (60%), verification set (20%) and test set (20%) random_indices = torch.randperm(dataset_tensor.shape[0]) traning_indices = random_indices[:int(len(random_indices)*0.6)] validating_indices = random_indices[int(len(random_indices)*0.6):int(len(random_indices)*0.8):] testing_indices = random_indices[int(len(random_indices)*0.8):] training_set = dataset_tensor[traning_indices] validating_set = dataset_tensor[validating_indices] testing_set = dataset_tensor[testing_indices] # Save to hard disk save_tensor(training_set, f"data/training_set.{batch}.pt") save_tensor(validating_set, f"data/validating_set.{batch}.pt") save_tensor(testing_set, f"data/testing_set.{batch}.pt") print(f"batch {batch} saved") def train(): """Start training""" # Create model instance model = MyModel() # Create loss calculator loss_function = torch.nn.MSELoss() # Create parameter adjuster optimizer = torch.optim.SGD(model.parameters(), lr=0.0000001) # Record the change of accuracy of training set and verification set traning_accuracy_history = [] validating_accuracy_history = [] # Record the highest verification set accuracy validating_accuracy_highest = 0 validating_accuracy_highest_epoch = 0 # Tool functions to read batches def read_batches(base_path): for batch in itertools.count(): path = f"{base_path}.{batch}.pt" if not os.path.isfile(path): break yield load_tensor(path) # Tool function for calculating accuracy def calc_accuracy(actual, predicted): return max(0, 1 - ((actual - predicted).abs() / actual.abs()).mean().item()) # Start the training process for epoch in range(1, 10000): print(f"epoch: {epoch}") # Train and modify parameters according to training set # Switching the model to training mode will enable automatic differentiation, batchnorm and Dropout model.train() traning_accuracy_list = [] for batch in read_batches("data/training_set"): # Segmentation of small batches helps to generalize the model for index in range(0, batch.shape[0], 100): # Divide input and output batch_x = batch[index:index+100,:-1] batch_y = batch[index:index+100,-1:] # Calculate forecast predicted = model(batch_x) # Calculate loss loss = loss_function(predicted, batch_y) # Derivation function value from loss automatic differentiation loss.backward() # Adjust parameters with parameter adjuster optimizer.step() # Clear the value of the function optimizer.zero_grad() # Record the correct rate of this batch. Torch.no-grad means to temporarily disable the automatic differentiation function with torch.no_grad(): traning_accuracy_list.append(calc_accuracy(batch_y, predicted)) traning_accuracy = sum(traning_accuracy_list) / len(traning_accuracy_list) traning_accuracy_history.append(traning_accuracy) print(f"training accuracy: {traning_accuracy}") # Check validation set # Switching the model to validation mode will disable automatic differentiation, batchnorm and Dropout model.eval() validating_accuracy_list = [] for batch in read_batches("data/validating_set"): validating_accuracy_list.append(calc_accuracy(batch[:,-1:], model(batch[:,:-1]))) validating_accuracy = sum(validating_accuracy_list) / len(validating_accuracy_list) validating_accuracy_history.append(validating_accuracy) print(f"validating accuracy: {validating_accuracy}") # Record the highest verification set accuracy and the current model state, and judge whether the record has not been refreshed after 100 trainings if validating_accuracy > validating_accuracy_highest: validating_accuracy_highest = validating_accuracy validating_accuracy_highest_epoch = epoch save_tensor(model.state_dict(), "model.pt") print("highest validating accuracy updated") elif epoch - validating_accuracy_highest_epoch > 100: # After 100 times of training, I still haven't refreshed the record. End the training print("stop training because highest validating accuracy not updated in 100 epoches") break # Use the model state at the highest accuracy print(f"highest validating accuracy: {validating_accuracy_highest}", f"from epoch {validating_accuracy_highest_epoch}") model.load_state_dict(load_tensor("model.pt")) # Check test set testing_accuracy_list = [] for batch in read_batches("data/testing_set"): testing_accuracy_list.append(calc_accuracy(batch[:,-1:], model(batch[:,:-1]))) testing_accuracy = sum(testing_accuracy_list) / len(testing_accuracy_list) print(f"testing accuracy: {testing_accuracy}") # Display the change of accuracy of training set and verification set pyplot.plot(traning_accuracy_history, label="traning") pyplot.plot(validating_accuracy_history, label="validing") pyplot.ylim(0, 1) pyplot.legend() pyplot.show() def eval_model(): """Using a trained model""" parameters = [ "Age", "Gender (0: Male, 1: Female)", "Years of work experience", "Java Skill (0 ~ 5)", "NET Skill (0 ~ 5)", "JS Skill (0 ~ 5)", "CSS Skill (0 ~ 5)", "HTML Skill (0 ~ 5)" ] # Create a model instance, load the trained state, and switch to validation mode model = MyModel() model.load_state_dict(load_tensor("model.pt")) model.eval() # Ask for input and predict output while True: try: x = torch.tensor([int(input(f"Your {p}: ")) for p in parameters], dtype=torch.float) # Convert to a matrix of 1 row and 1 column. In fact, it can not be converted here, but it is recommended to do so, because not all models support non batch input x = x.view(1, len(x)) y = model(x) print("Your estimated salary:", y[0,0].item(), "\n") except Exception as e: print("error:", e) def main(): """Main function""" if len(sys.argv) < 2: print(f"Please run: {sys.argv[0]} prepare|train|eval") exit() # Assign an initial value to the random number generator so that the same random number can be generated for each run # This is to make the process repeatable and you can choose not to torch.random.manual_seed(0) # Select actions based on command line parameters operation = sys.argv[1] if operation == "prepare": prepare() elif operation == "train": train() elif operation == "eval": eval_model() else: raise ValueError(f"Unsupported operation: {operation}") if __name__ == "__main__": main()
Execute the following command to go through the whole process. If you need to adjust the model, you can directly rerun train to avoid the time consumption of prepare:
python3 example.py prepare python3 example.py train python3 example.py eval
Note that the above code is different from the previous code in terms of data set scrambling and batch processing. The above code will read the csv file in sections, and then scrambling each section to subdivide the training set, verification set and test set, which can also ensure the data distribution in each set is uniform. The accuracy of the final training set and verification set changes as follows:
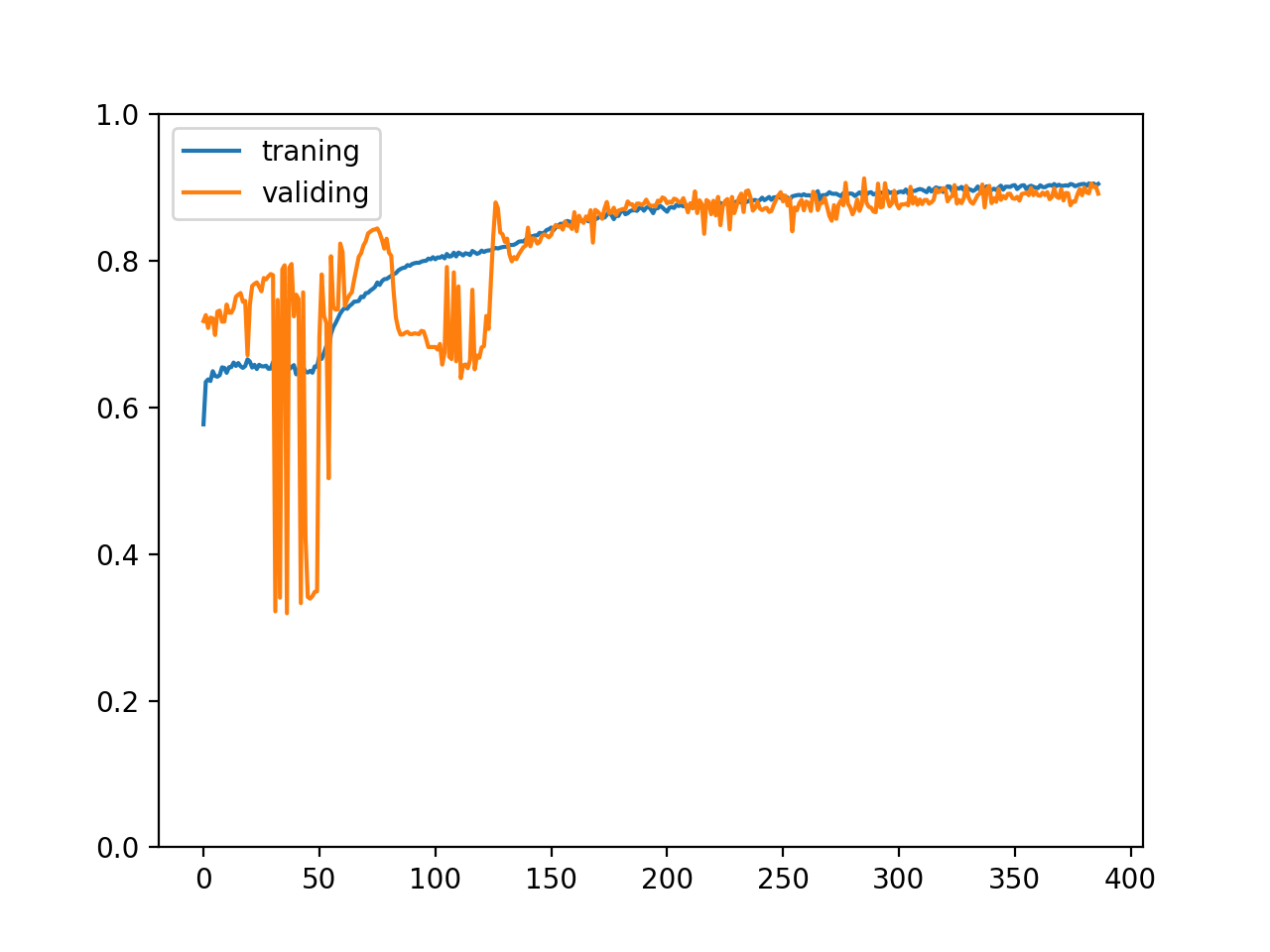
Normalize input and output values
So far, when we train, we directly give the original input value of the model, and then use the original output value to adjust the parameters. The problem is that if the input value is very large, the derivative function value will also be very large. If the output value is very large, we need to adjust the parameters many times. In the past, we used a very small learning ratio (0.0000001) To avoid this problem, but actually there is a better way, that is to normalize the input and output values. The normalization here refers to scaling the input and output values to a certain scale, so that most of the values fall in the range of -1 to 1. In the example of forecasting wages according to the conditions of farmers, we can multiply age and years of working experience by 0.01 (range: 0-100 years), skills by 0.02 (range: 0-5), wages by 0.0001 (unit: 10000), and perform the following operations on dataset ﹐ sensor:
# Multiply each row by the specified factor dataset_tensor *= torch.tensor([0.01, 1, 0.01, 0.2, 0.2, 0.2, 0.2, 0.2, 0.0001])
Then modify the learning ratio to 0.01:
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
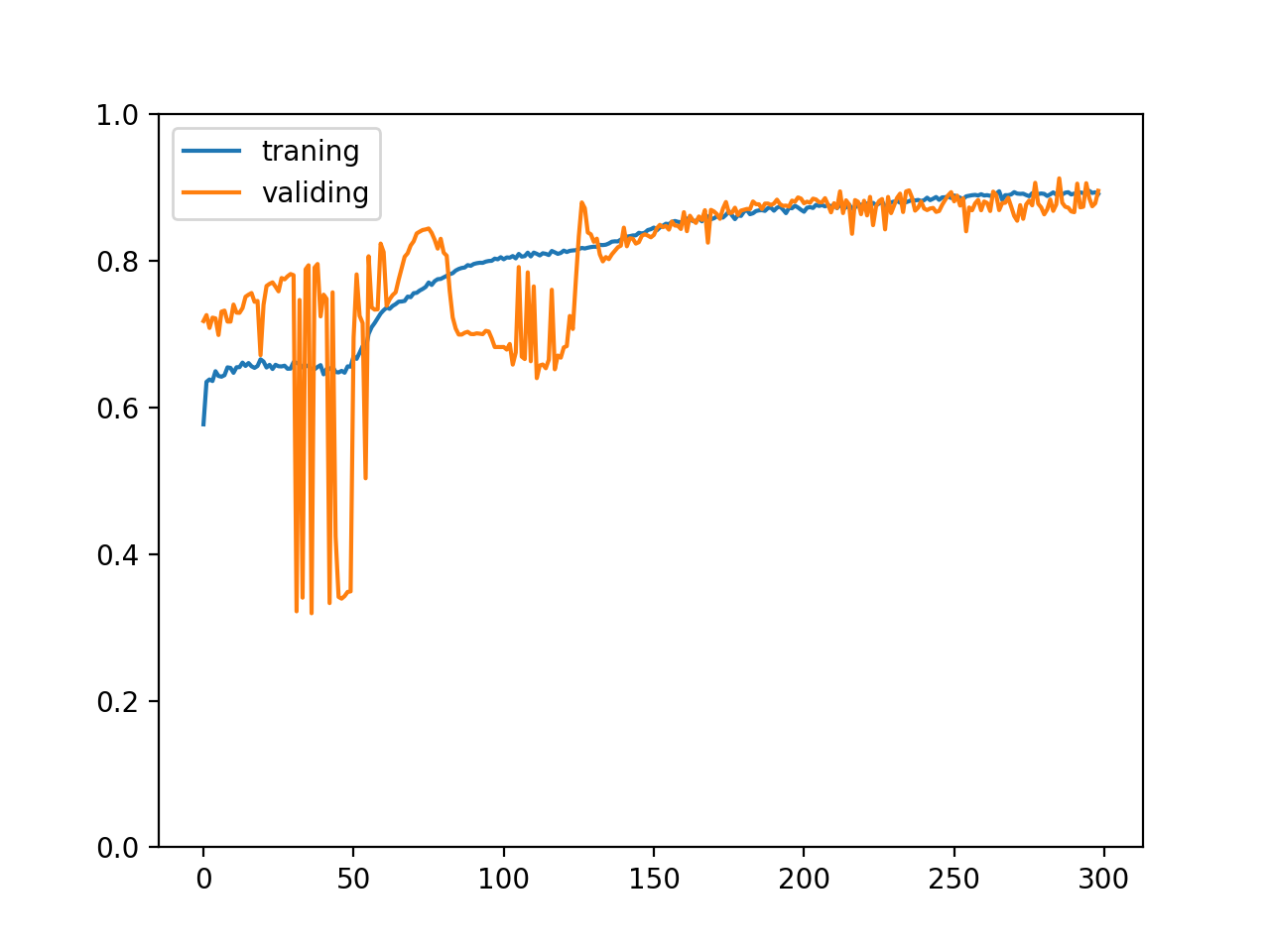
The change of the accuracy of 300 times of training is as follows:
Before normalizing input and output values
After normalizing input and output values
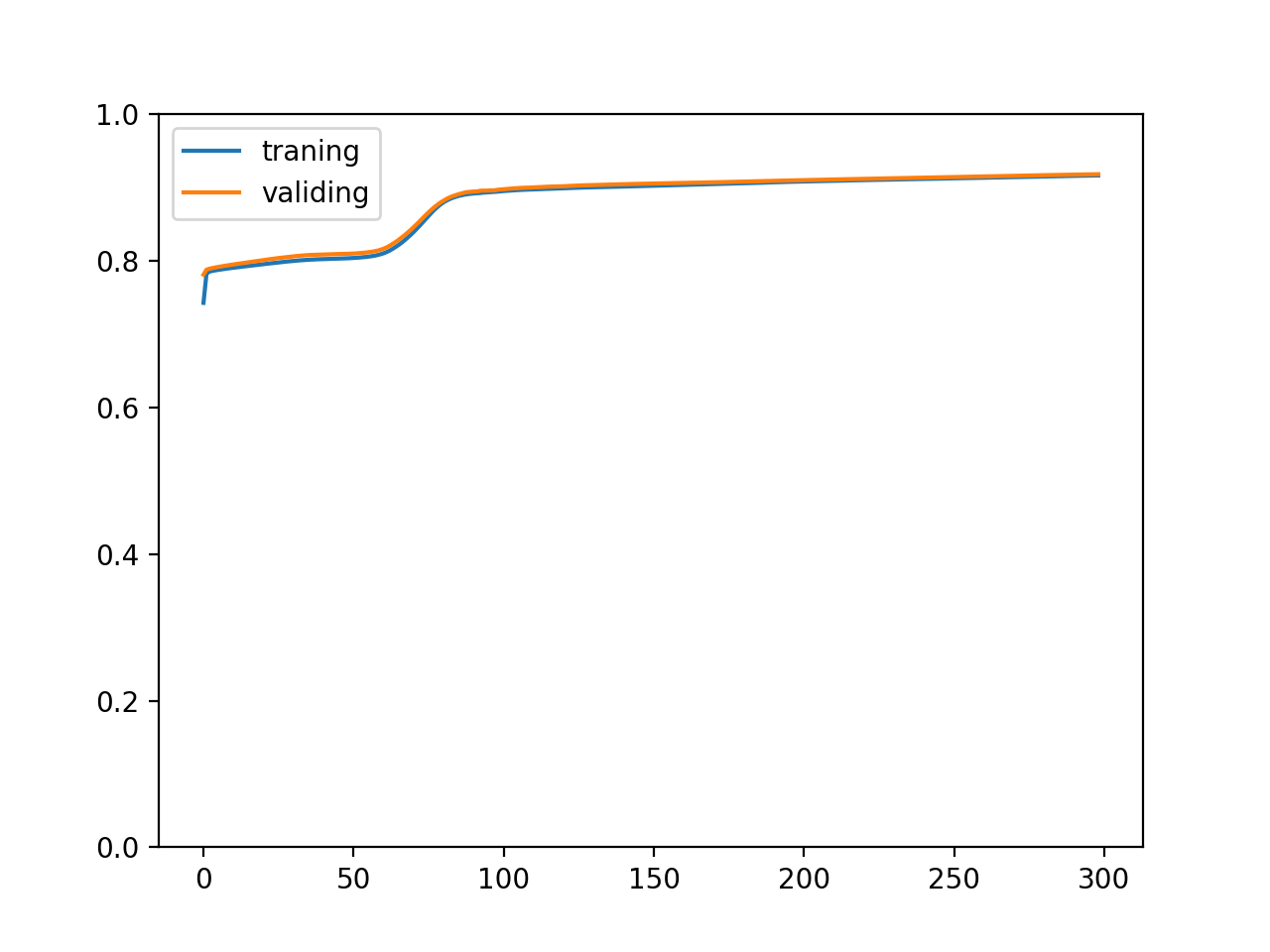
You can see the effect is quite amazing A kind of After normalizing the input and output values, the training speed becomes faster and the curve of correct rate changes much smoother. In fact, it is necessary to do this. If some data sets are not normalized, they cannot learn at all. Making the model receive and output smaller values (- 1-1 interval) can prevent the explosion of the value of the function and use a higher learning rate to speed up the training.
Also, don't forget to scale the input and output values when using the model:
x = torch.tensor([int(input(f"Your {p}: ")) for p in parameters], dtype=torch.float) x *= torch.tensor([0.01, 1, 0.01, 0.2, 0.2, 0.2, 0.2, 0.2]) # Convert to a matrix of 1 row and 1 column. In fact, it can not be converted here, but it is recommended to do so, because not all models support non batch input x = x.view(1, len(x)) y = model(x) * 10000 print("Your estimated salary:", y[0,0].item(), "\n")
Using Dropout to help generalize models
As mentioned in the previous content, if the model is too powerful or there are many data impurities, the model may adapt to the impurities in the data to achieve a higher accuracy (over fitting phenomenon). At this time, although the accuracy of the training set will rise, the accuracy of the verification set will maintain or even decline, and the model's ability to deal with unknown data will decline. To prevent over fitting and enhance the ability of the model to deal with unknown data is also called generalization model. One of the means of generalization model is to use Dropout, which will shield some neurons randomly during the training process, and let the output of these neurons be 0. At the same time, increase the output of unshielded neurons to make the total output close to the original level. The advantage of this is that the model will try to find out how to correctly predict the results (reduce the correlation between cross layer neurons) after a part of neurons are shielded, which eventually leads to the model to grasp the law of data more fully.
The following figure is an example of neural network after Dropout (3 inputs and 2 outputs, 5 hidden values for each layer of 3 layers):
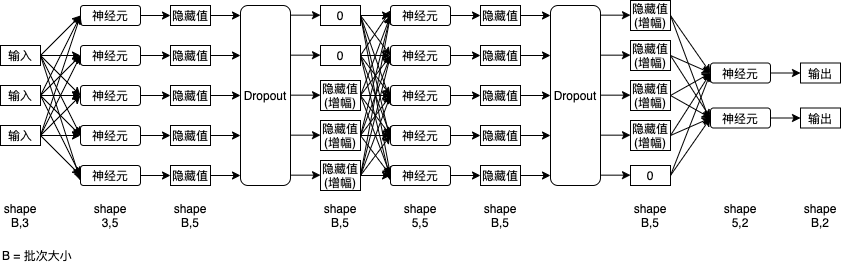
Next, let's see how to use Dropout in Python:
# Referencing the pytorch class library >>> import torch # Create Dropout functions that mask 20% >>> dropout = torch.nn.Dropout(0.2) # Define a sensor (assuming that the sensor is the output of a neural network layer) >>> a = torch.tensor(range(1, 11), dtype=torch.float) >>> a tensor([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]) # Apply Dropout function # We can see that the unshielded value will increase (divided by 0.8) to keep the total value at the original level # In addition, the number of shielding will fluctuate according to the probability, not necessarily 100% equal to the proportion we set (there are 1 shielding value and 3 shielding values here) >>> dropout(a) tensor([ 0.0000, 2.5000, 3.7500, 5.0000, 6.2500, 7.5000, 8.7500, 10.0000, 11.2500, 12.5000]) >>> dropout(a) tensor([ 1.2500, 2.5000, 3.7500, 5.0000, 6.2500, 7.5000, 8.7500, 0.0000, 11.2500, 0.0000]) >>> dropout(a) tensor([ 1.2500, 2.5000, 3.7500, 5.0000, 6.2500, 7.5000, 8.7500, 0.0000, 11.2500, 12.5000]) >>> dropout(a) tensor([ 1.2500, 2.5000, 3.7500, 5.0000, 6.2500, 7.5000, 0.0000, 10.0000, 11.2500, 0.0000]) >>> dropout(a) tensor([ 1.2500, 2.5000, 3.7500, 5.0000, 0.0000, 7.5000, 8.7500, 10.0000, 11.2500, 0.0000]) >>> dropout(a) tensor([ 1.2500, 2.5000, 0.0000, 5.0000, 0.0000, 7.5000, 8.7500, 10.0000, 11.2500, 12.5000]) >>> dropout(a) tensor([ 0.0000, 2.5000, 3.7500, 5.0000, 6.2500, 7.5000, 0.0000, 10.0000, 0.0000, 0.0000])
Next, let's see how to apply Dropout to the model. First, we can reproduce the over fitting phenomenon, increase the number of neurons in the model and reduce the amount of data in the training set
Code of model part:
class MyModel(nn.Module): """A model for forecasting wages based on the condition of farmers""" def __init__(self): super().__init__() self.layer1 = nn.Linear(in_features=8, out_features=200) self.layer2 = nn.Linear(in_features=200, out_features=100) self.layer3 = nn.Linear(in_features=100, out_features=1) def forward(self, x): hidden1 = nn.functional.relu(self.layer1(x)) hidden2 = nn.functional.relu(self.layer2(hidden1)) y = self.layer3(hidden2) return y
Code of training part (only the first 16 data of each batch are trained):
for batch in read_batches("data/training_set"): # Segmentation of small batches helps to generalize the model for index in range(0, batch.shape[0], 16): # Divide input and output batch_x = batch[index:index+16,:-1] batch_y = batch[index:index+16,-1:] # Calculate forecast predicted = model(batch_x) # Calculate loss loss = loss_function(predicted, batch_y) # Derivation function value from loss automatic differentiation loss.backward() # Adjust parameters with parameter adjuster optimizer.step() # Clear the value of the function optimizer.zero_grad() # Record the correct rate of this batch. Torch.no-grad means to temporarily disable the automatic differentiation function with torch.no_grad(): traning_accuracy_list.append(calc_accuracy(batch_y, predicted)) # Only the first 16 data break
The correct rate of fixed training after 1000 times:
training accuracy: 0.9706422178819776 validating accuracy: 0.8514168351888657 highest validating accuracy: 0.8607834208011628 from epoch 223 testing accuracy: 0.8603586450219154
And the trend of the change of accuracy rate:
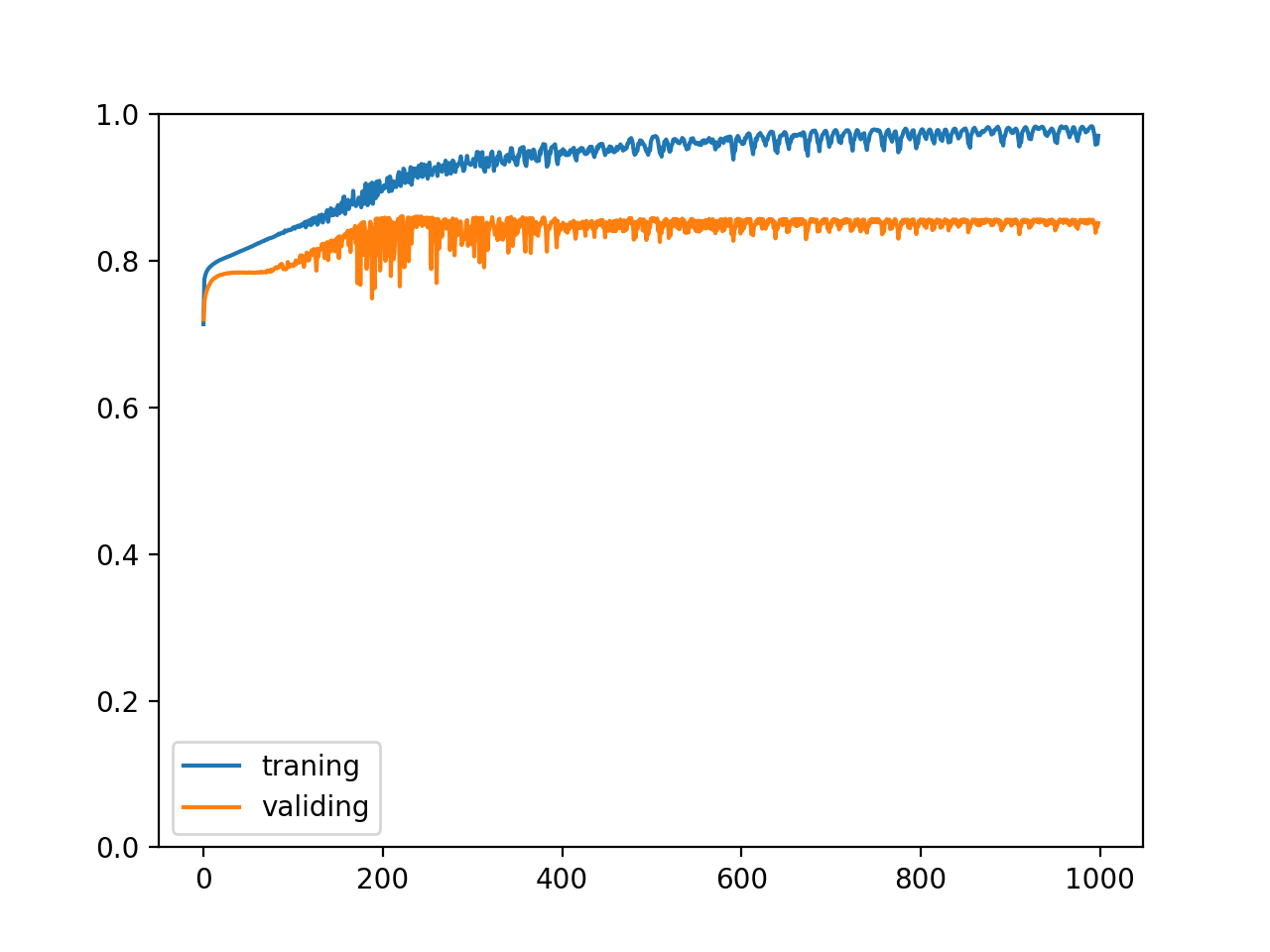
Try to add two dropouts to the model, corresponding to the output (hidden value) of the first and second layers respectively:
class MyModel(nn.Module): """A model for forecasting wages based on the condition of farmers""" def __init__(self): super().__init__() self.layer1 = nn.Linear(in_features=8, out_features=200) self.layer2 = nn.Linear(in_features=200, out_features=100) self.layer3 = nn.Linear(in_features=100, out_features=1) self.dropout1 = nn.Dropout(0.2) self.dropout2 = nn.Dropout(0.2) def forward(self, x): hidden1 = self.dropout1(nn.functional.relu(self.layer1(x))) hidden2 = self.dropout2(nn.functional.relu(self.layer2(hidden1))) y = self.layer3(hidden2) return y
At this time, the following accuracy rate will be obtained after training:
training accuracy: 0.9326518730819225 validating accuracy: 0.8692235469818115 highest validating accuracy: 0.8728838726878166 from epoch 867 testing accuracy: 0.8733032837510109
And the trend of the change of accuracy rate:
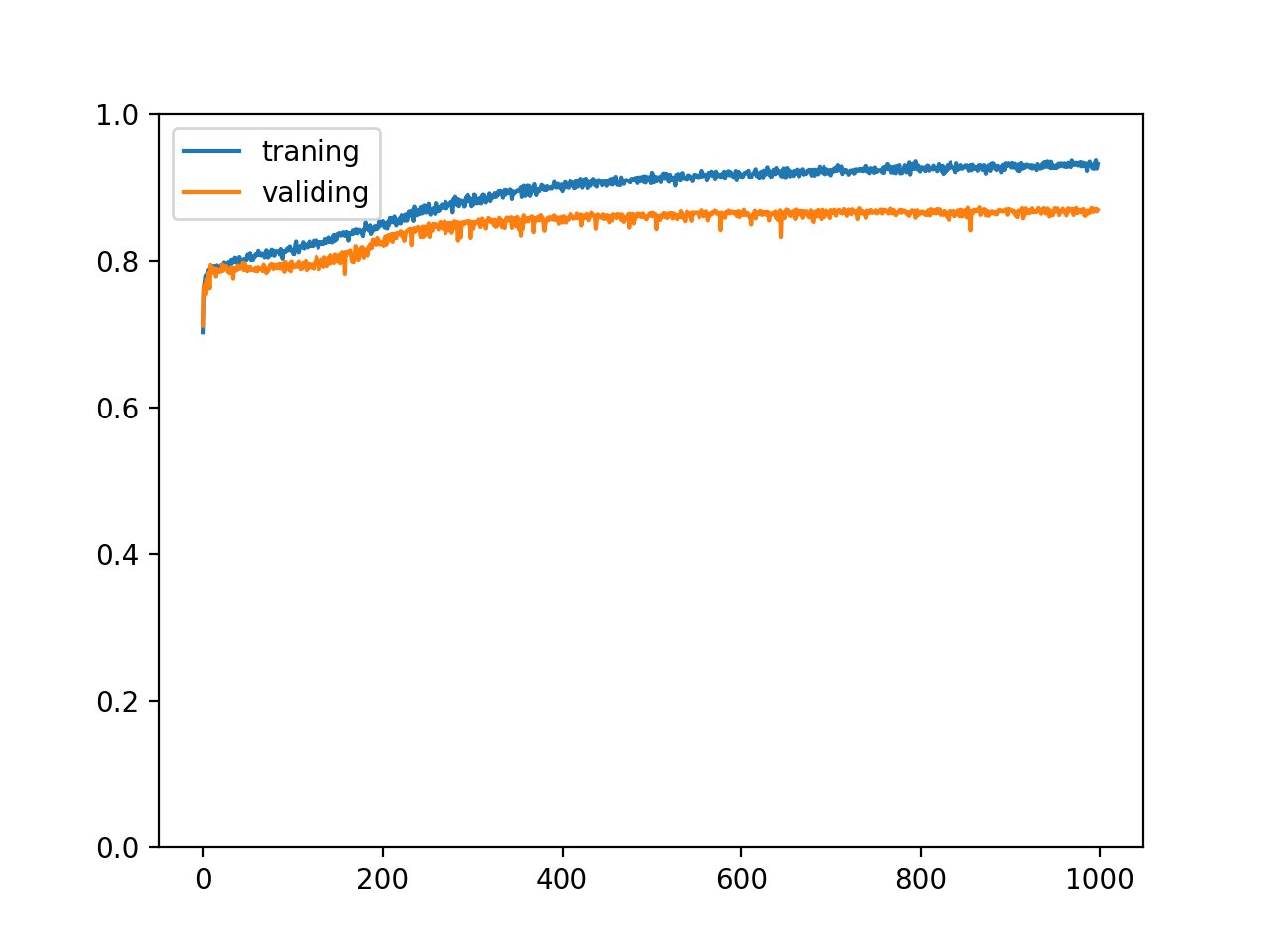
We can see that the correct rate of training set does not increase blindly, and the correct rate of verification set and test set has increased by more than 1%, which shows that Dropout has a certain effect.
You should pay attention to the following points when using Dropout:
- Dropout should be used for hidden values, not before the first layer (for input) or after the last layer (for output)
- Dropout should be placed after the activation function (because the activation function is part of the neuron)
- Dropout should only be used during training. When evaluating or actually using a model, model.eval() should be called to switch the model to evaluation mode to prevent dropout
- The Dropout function should be defined as a member of the model so that a call to model.eval() can index all the Dropout functions corresponding to the model
- Dropout has no optimal shielding ratio. You can try several times to find the best result for the current data and model
The original paper that put forward the Dropout technique Here , if you are interested, you can view it.
Normalize batches with BatchNorm
BatchNorm is another way to improve the training effect. In some scenarios, it can improve the training efficiency and inhibit over fitting. BatchNorm is used for hidden values like Dropout, and normalizes each value (each column) of each batch. The calculation formula is as follows:

In summary, let each value in each column subtract the average value of this column, then divide by the standard deviation of this column, and then adjust it in a certain proportion.
An example of using BatchNorm in python is as follows:
# Create batchnorm function, 3 represents the number of columns >>> batchnorm = torch.nn.BatchNorm1d(3) # View the weights and offsets within the batchnorm function >>> list(batchnorm.parameters()) [Parameter containing: tensor([1., 1., 1.], requires_grad=True), Parameter containing: tensor([0., 0., 0.], requires_grad=True)] # Randomly create a sensor with 10 rows and 3 columns >>> a = torch.rand((10, 3)) >>> a tensor([[0.9643, 0.6933, 0.0039], [0.3967, 0.8239, 0.3490], [0.4011, 0.8903, 0.3053], [0.0666, 0.5766, 0.4976], [0.4928, 0.1403, 0.8900], [0.7317, 0.9461, 0.1816], [0.4461, 0.9987, 0.8324], [0.3714, 0.6550, 0.9961], [0.4852, 0.7415, 0.1779], [0.6876, 0.1538, 0.3429]]) # Applying batchnorm function >>> batchnorm(a) tensor([[ 1.9935, 0.1096, -1.4156], [-0.4665, 0.5665, -0.3391], [-0.4477, 0.7985, -0.4754], [-1.8972, -0.2986, 0.1246], [-0.0501, -1.8245, 1.3486], [ 0.9855, 0.9939, -0.8611], [-0.2523, 1.1776, 1.1691], [-0.5761, -0.0243, 1.6798], [-0.0831, 0.2783, -0.8727], [ 0.7941, -1.7770, -0.3581]], grad_fn=<NativeBatchNormBackward>) # Manual reproduction of batchnorm's calculation of the first column >>> aa = a[:,:1] >>> aa tensor([[0.9643], [0.3967], [0.4011], [0.0666], [0.4928], [0.7317], [0.4461], [0.3714], [0.4852], [0.6876]]) >>> (aa - aa.mean()) / (((aa - aa.mean()) ** 2).mean() + 0.00001).sqrt() tensor([[ 1.9935], [-0.4665], [-0.4477], [-1.8972], [-0.0501], [ 0.9855], [-0.2523], [-0.5761], [-0.0831], [ 0.7941]])
Modify the model to use BatchNorm as follows:
class MyModel(nn.Module): """A model for forecasting wages based on the condition of farmers""" def __init__(self): super().__init__() self.layer1 = nn.Linear(in_features=8, out_features=200) self.layer2 = nn.Linear(in_features=200, out_features=100) self.layer3 = nn.Linear(in_features=100, out_features=1) self.batchnorm1 = nn.BatchNorm1d(200) self.batchnorm2 = nn.BatchNorm1d(100) self.dropout1 = nn.Dropout(0.1) self.dropout2 = nn.Dropout(0.1) def forward(self, x): hidden1 = self.dropout1(self.batchnorm1(nn.functional.relu(self.layer1(x)))) hidden2 = self.dropout2(self.batchnorm2(nn.functional.relu(self.layer2(hidden1)))) y = self.layer3(hidden2) return y
The learning rate needs to be adjusted at the same time:
# Create parameter adjuster optimizer = torch.optim.SGD(model.parameters(), lr=0.05)
The results of 1000 times of fixed training are as follows. You can see that BatchNorm does not play a role in this scenario, but slows down the learning speed and affects the highest accuracy that can be achieved (you can try to increase the training times):
training accuracy: 0.9048486271500588 validating accuracy: 0.8341873311996459 highest validating accuracy: 0.8443503141403198 from epoch 946 testing accuracy: 0.8452585405111313
The following points should be noted when using BatchNorm:
- BatchNorm should be used for hidden values, just like Dropout
- BatchNorm needs to specify the number of hidden values, which should match the output number of the corresponding layer
- BatchNorm should be put in front of Dropout. Some people will choose to put BatchNorm in front of the activation function, and some people will choose to put it after the activation function
- Linear => ReLU => BatchNorm => Dropout
- Linear => BatchNorm => ReLU => Dropout
- BatchNorm should only be used during training, just like Dropout
- The BatchNorm function should be defined as a member of the model, just like Dropout
- When using BatchNorm, the shielding ratio of Dropout should be reduced accordingly
- Some scenarios may not be applicable to BatchNorm (it is said that they are more suitable for object recognition and picture classification), which requires practice to produce real knowledge
The original paper that put forward BatchNorm technique Here , if you are interested, you can view it.
Understand the eval and train patterns of the model
In the previous example, we used eval and train functions to switch between evaluation mode and training mode. Evaluation mode will disable automatic differentiation, Dropout and BatchNorm. How are these two modes implemented?
The model of Python is based on the class of torch.nn.Module, which is not only our own defined model, nn.Sequential, nn.Linear, nn.ReLU, nn.Dropout, nn.BatchNorm1d and other types are based on torch.nn.Module. Torch.nn.Module has a training member to represent whether the model is in training mode. The eval function is used to recursively set the training of all modules to False, and the train function is used to recursively set the training of all modules to True. We can manually set this member to see if it can achieve the same effect:
>>> a = torch.tensor(range(1, 11), dtype=torch.float) >>> dropout = torch.nn.Dropout(0.2) >>> dropout.training = False >>> dropout(a) tensor([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]) >>> dropout.training = True >>> dropout(a) tensor([ 1.2500, 2.5000, 3.7500, 0.0000, 0.0000, 7.5000, 8.7500, 10.0000, 0.0000, 12.5000])
With this in mind, you can add code to the model that only executes during training or evaluation, as judged by self.training.
Final code
The final code of salary forecast according to the conditions of farmers is as follows:
import os import sys import pandas import torch import gzip import itertools from torch import nn from matplotlib import pyplot class MyModel(nn.Module): """A model for forecasting wages based on the condition of farmers""" def __init__(self): super().__init__() self.layer1 = nn.Linear(in_features=8, out_features=200) self.layer2 = nn.Linear(in_features=200, out_features=100) self.layer3 = nn.Linear(in_features=100, out_features=1) self.batchnorm1 = nn.BatchNorm1d(200) self.batchnorm2 = nn.BatchNorm1d(100) self.dropout1 = nn.Dropout(0.1) self.dropout2 = nn.Dropout(0.1) def forward(self, x): hidden1 = self.dropout1(self.batchnorm1(nn.functional.relu(self.layer1(x)))) hidden2 = self.dropout2(self.batchnorm2(nn.functional.relu(self.layer2(hidden1)))) y = self.layer3(hidden2) return y def save_tensor(tensor, path): """Preservation tensor Object to file""" torch.save(tensor, gzip.GzipFile(path, "wb")) def load_tensor(path): """Read from file tensor object""" return torch.load(gzip.GzipFile(path, "rb")) def prepare(): """Prepare for training""" # The dataset will be saved in the data folder after it is converted to the sensor if not os.path.isdir("data"): os.makedirs("data") # Read the original data set from csv, 2000 lines at a time in batches for batch, df in enumerate(pandas.read_csv('salary.csv', chunksize=2000)): dataset_tensor = torch.tensor(df.values, dtype=torch.float) # Normalize input and output dataset_tensor *= torch.tensor([0.01, 1, 0.01, 0.2, 0.2, 0.2, 0.2, 0.2, 0.0001]) # Segmentation training set (60%), verification set (20%) and test set (20%) random_indices = torch.randperm(dataset_tensor.shape[0]) traning_indices = random_indices[:int(len(random_indices)*0.6)] validating_indices = random_indices[int(len(random_indices)*0.6):int(len(random_indices)*0.8):] testing_indices = random_indices[int(len(random_indices)*0.8):] training_set = dataset_tensor[traning_indices] validating_set = dataset_tensor[validating_indices] testing_set = dataset_tensor[testing_indices] # Save to hard disk save_tensor(training_set, f"data/training_set.{batch}.pt") save_tensor(validating_set, f"data/validating_set.{batch}.pt") save_tensor(testing_set, f"data/testing_set.{batch}.pt") print(f"batch {batch} saved") def train(): """Start training""" # Create model instance model = MyModel() # Create loss calculator loss_function = torch.nn.MSELoss() # Create parameter adjuster optimizer = torch.optim.SGD(model.parameters(), lr=0.05) # Record the change of accuracy of training set and verification set traning_accuracy_history = [] validating_accuracy_history = [] # Record the highest verification set accuracy validating_accuracy_highest = 0 validating_accuracy_highest_epoch = 0 # Tool functions to read batches def read_batches(base_path): for batch in itertools.count(): path = f"{base_path}.{batch}.pt" if not os.path.isfile(path): break yield load_tensor(path) # Tool function for calculating accuracy def calc_accuracy(actual, predicted): return max(0, 1 - ((actual - predicted).abs() / actual.abs()).mean().item()) # Start the training process for epoch in range(1, 10000): print(f"epoch: {epoch}") # Train and modify parameters according to training set # Switching the model to training mode will enable automatic differentiation, batchnorm and Dropout model.train() traning_accuracy_list = [] for batch in read_batches("data/training_set"): # Segmentation of small batches helps to generalize the model for index in range(0, batch.shape[0], 100): # Divide input and output batch_x = batch[index:index+100,:-1] batch_y = batch[index:index+100,-1:] # Calculate forecast predicted = model(batch_x) # Calculate loss loss = loss_function(predicted, batch_y) # Derivation function value from loss automatic differentiation loss.backward() # Adjust parameters with parameter adjuster optimizer.step() # Clear the value of the function optimizer.zero_grad() # Record the correct rate of this batch. Torch.no-grad means to temporarily disable the automatic differentiation function with torch.no_grad(): traning_accuracy_list.append(calc_accuracy(batch_y, predicted)) traning_accuracy = sum(traning_accuracy_list) / len(traning_accuracy_list) traning_accuracy_history.append(traning_accuracy) print(f"training accuracy: {traning_accuracy}") # Check validation set # Switching the model to validation mode will disable automatic differentiation, batchnorm and Dropout model.eval() validating_accuracy_list = [] for batch in read_batches("data/validating_set"): validating_accuracy_list.append(calc_accuracy(batch[:,-1:], model(batch[:,:-1]))) validating_accuracy = sum(validating_accuracy_list) / len(validating_accuracy_list) validating_accuracy_history.append(validating_accuracy) print(f"validating accuracy: {validating_accuracy}") # Record the highest verification set accuracy and the current model state, and judge whether the record has not been refreshed after 100 trainings if validating_accuracy > validating_accuracy_highest: validating_accuracy_highest = validating_accuracy validating_accuracy_highest_epoch = epoch save_tensor(model.state_dict(), "model.pt") print("highest validating accuracy updated") elif epoch - validating_accuracy_highest_epoch > 100: # After 100 times of training, I still haven't refreshed the record. End the training print("stop training because highest validating accuracy not updated in 100 epoches") break # Use the model state at the highest accuracy print(f"highest validating accuracy: {validating_accuracy_highest}", f"from epoch {validating_accuracy_highest_epoch}") model.load_state_dict(load_tensor("model.pt")) # Check test set testing_accuracy_list = [] for batch in read_batches("data/testing_set"): testing_accuracy_list.append(calc_accuracy(batch[:,-1:], model(batch[:,:-1]))) testing_accuracy = sum(testing_accuracy_list) / len(testing_accuracy_list) print(f"testing accuracy: {testing_accuracy}") # Display the change of accuracy of training set and verification set pyplot.plot(traning_accuracy_history, label="traning") pyplot.plot(validating_accuracy_history, label="validing") pyplot.ylim(0, 1) pyplot.legend() pyplot.show() def eval_model(): """Using a trained model""" parameters = [ "Age", "Gender (0: Male, 1: Female)", "Years of work experience", "Java Skill (0 ~ 5)", "NET Skill (0 ~ 5)", "JS Skill (0 ~ 5)", "CSS Skill (0 ~ 5)", "HTML Skill (0 ~ 5)" ] # Create a model instance, load the trained state, and switch to validation mode model = MyModel() model.load_state_dict(load_tensor("model.pt")) model.eval() # Ask for input and predict output while True: try: x = torch.tensor([int(input(f"Your {p}: ")) for p in parameters], dtype=torch.float) # Normalized input x *= torch.tensor([0.01, 1, 0.01, 0.2, 0.2, 0.2, 0.2, 0.2]) # Convert to a matrix of 1 row and 1 column. In fact, it can not be converted here, but it is recommended to do so, because not all models support non batch input x = x.view(1, len(x)) # Forecast output y = model(x) # Arcuated output y *= 10000 print("Your estimated salary:", y[0,0].item(), "\n") except Exception as e: print("error:", e) def main(): """Main function""" if len(sys.argv) < 2: print(f"Please run: {sys.argv[0]} prepare|train|eval") exit() # Assign an initial value to the random number generator so that the same random number can be generated for each run # This is to make the process repeatable and you can choose not to torch.random.manual_seed(0) # Select actions based on command line parameters operation = sys.argv[1] if operation == "prepare": prepare() elif operation == "train": train() elif operation == "eval": eval_model() else: raise ValueError(f"Unsupported operation: {operation}") if __name__ == "__main__": main()
The final training results are as follows: the accuracy of verification set and test set is 94.3% (93.3% and 93.1% respectively in the previous article)
epoch: 848 training accuracy: 0.929181088420252 validating accuracy: 0.9417830203473568 stop training because highest validating accuracy not updated in 100 epoches highest validating accuracy: 0.9437697219848633 from epoch 747 testing accuracy: 0.9438129015266895
The accuracy changes are as follows:
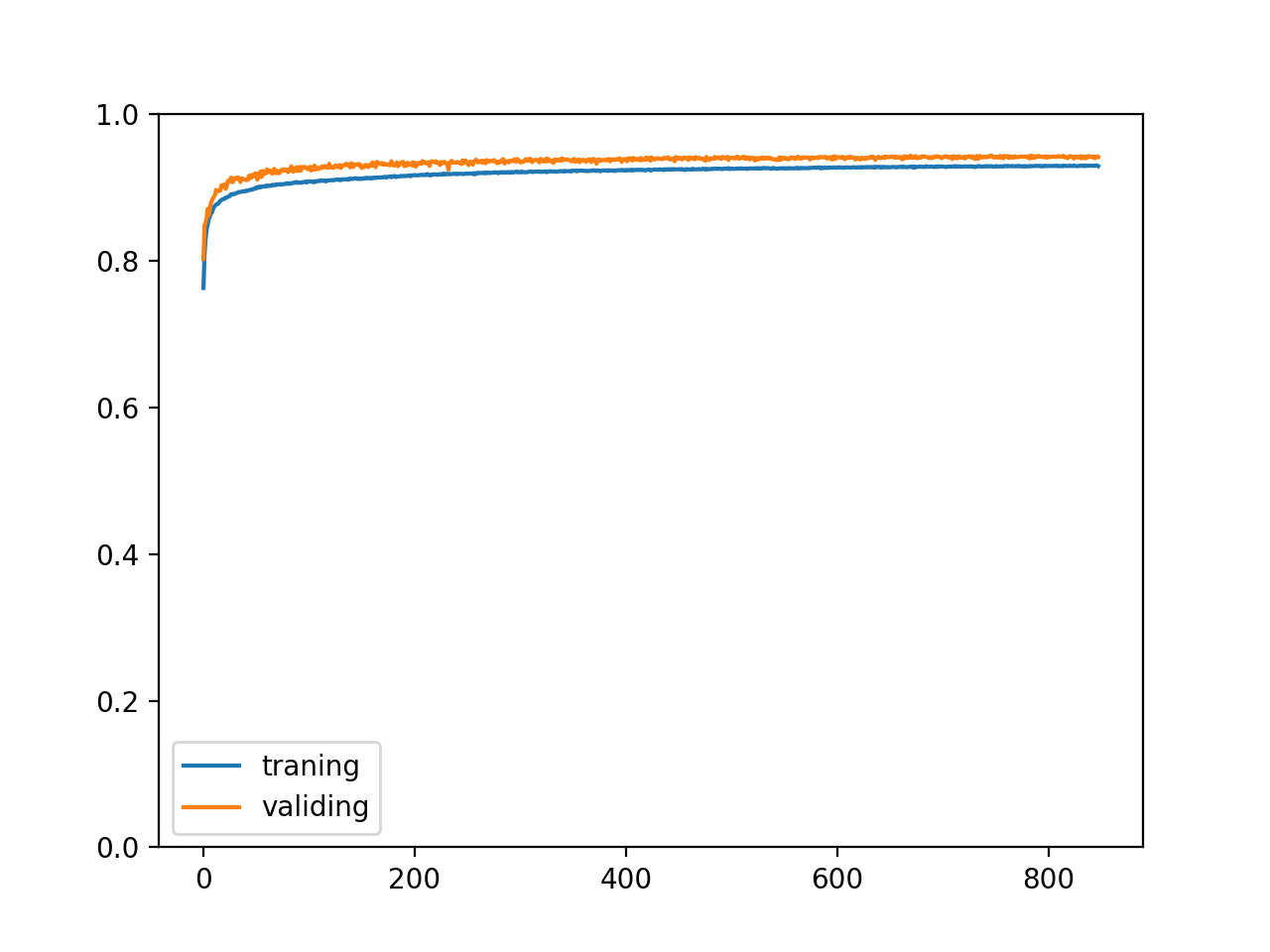
It was a complete success.
Write at the end
In this article, we see various ways to improve the training process and training effect, and predict the wages of various farmers A kind of , then we can try to do something different. In the next section, we will introduce RNN, LSTM and GRU, which can be used to process indefinite length data, realize the functions of classification according to context, trend prediction and automatic completion.