Binary tree isomorphism
Isomorphism of tree:
Give two trees T1 and T2. If T1 can be changed into T2 by several times, we call the two trees "isomorphic". For example, the two trees given in Figure 1 are isomorphic, because we exchange the left and right children of nodes A, B and G of one tree to get the other tree. Figure 2 is not isomorphic.
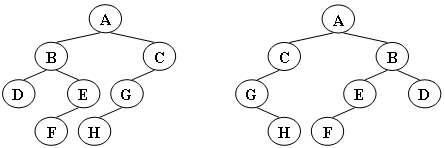
Figure 1

Figure 2
Chained storage binary tree
Algorithm:
int Isomorphic(Tree T1, Tree T2)
{
if (!T1 && !T2)return 1;//Both trees are empty and isomorphic
if (!T1 && T2 || T1 && !T2 || T1->Element != T2->Element)
return 0;//If one tree is empty and the other tree is not empty, it is not isomorphic; The elements of the two trees are different and not isomorphic
return Isomorphic(T1->Left, T2->Left) && Isomorphic(T1->Right, T2->Right) || Isomorphic(T1->Left, T2->Right) && Isomorphic(T1->Right, T2->Left);
//(T1 left subtree is isomorphic with T2 left subtree and T1 right subtree is isomorphic with T2 right subtree) or (T1 left subtree is isomorphic with T2 right subtree and T1 right subtree is isomorphic with T2 left subtree)
}
Array storage binary tree
Example:
Input format:
Input the information of 2 binary trees. For each tree, first give a non negative integer n (≤ 10) in one row, that is, the number of nodes of the tree (at this time, it is assumed that the nodes are numbered from 0 to n − 1); Then, line N and line I correspond to the i-th node, giving one English capital letter stored in the node, the number of its left child node and the number of its right child node. If the child node is empty, a "-" will be given at the corresponding position. The data given are separated by a space. Note: the title ensures that the letters stored in each node are different.
Output format:
If the two trees are isomorphic, output "Yes", otherwise output "No".
Input example 1 (corresponding to figure 1):
8 A 1 2 B 3 4 C 5 - D - - E 6 - G 7 - F - - H - - 8 G - 4 B 7 6 F - - A 5 1 H - - C 0 - D - - E 2 - No blank lines at the end
Output example 1:
Yes No blank lines at the end
Algorithm:
#include <stdio.h>
#include <stdlib.h>
#define N 11
int n;
typedef struct TNode
{
char data;
int Left, Right;
}TNode;
TNode T1[N], T2[N];
int Create(TNode node[])
{
int i, check[N] = { 0 };
//TNode node[N];//
char ch;
scanf("%d", &n);
getchar();
if(!n)return -1;//Empty tree condition
for (i = 0; i < n; i++)
{
scanf("%c", &node[i].data);
getchar();
scanf("%c", &ch);
getchar();
if (ch == '-')node[i].Left = -1;
else
{
node[i].Left = ch - '0';
check[node[i].Left] = 1;
}
scanf("%c", &ch);
getchar();
if (ch == '-')node[i].Right = -1;
else
{
node[i].Right = ch - '0';
check[node[i].Right] = 1;
}
}
for (i = 0; check[i]; i++);
return i;
}
int IsTongGou(int root1, int root2)//Compared with a binary tree stored in a chain, the transmitted parameter is still "address" (the subscript of the node)
{
if (root1 == -1 && root2 == -1)return 1;
if (root1 == -1 && root2 != -1 || root1 != -1 && root2 == -1 || T1[root1].data != T2[root2].data)return 0;
return IsTongGou(T1[root1].Left, T2[root2].Left) && IsTongGou(T1[root1].Right, T2[root2].Right) || IsTongGou(T1[root1].Left, T2[root2].Right) && IsTongGou(T1[root1].Right, T2[root2].Left);
}
int main()
{
int t1, t2;
t1 = Create(T1);
t2 = Create(T2);
if (IsTongGou(t1, t2))printf("Yes");
else printf("No");
return 0;
}
Binary tree - height
Idea:
Traverse the left and right subtrees respectively, and return the maximum height + 1 and the height of the tree
Algorithm:
int Height(Tree T)
{
int Lh, Rh;
if (!T)return 0;
Lh = Height(T->Left);
Rh = Height(T->Right);
if (Lh > Rh)return Lh + 1;
else return Rh + 1;
}
Binary tree - restore
Known preorder and middle order
Given the preorder traversal sequence and middle order traversal sequence of a binary tree, it is required to calculate the height of the binary tree.
Idea:
- Determine the root node according to the result of preorder traversal. The first node traversed in sequence is the root node.
- Find the root node in the middle order traversal result. The left part of the root node is the left subtree node, and the right part of the root node is the right subtree node.
- The result of the middle order traversal is divided into two parts according to the root node. The first step and the second step are performed iteratively until the whole binary tree is restored.
explain:
Root: the root node traversed first
begin: find the starting point of the root node in the middle order traversal result
len: number of nodes in the tree
Algorithm:
#include <stdio.h>
#include <stdlib.h>
#define MAX 100
typedef struct TreeNode
{
char data;
struct TreeNode* Left, * Right;
}*Tree;
char Pre[MAX], In[MAX];
Tree RCreate(int root, int begin, int len)
{
int i;
if (len <= 0)return NULL;
Tree T;
T = (Tree)malloc(sizeof(struct TreeNode));
if (!T)exit(0);
T->data = Pre[root];
for (i = 0; Pre[root] == In[begin + i]; i++);
T->Left = RCreate(root + 1, begin, i);
T->Right = RCreate(root + i + 1, begin + i + 1, len - i - 1);
return T;
}
int Height(Tree T)
{
if (!T)return 0;
int Lh, Rh;
Lh = Height(T->Left);
Rh = Height(T->Right);
return Lh > Rh ? Lh + 1 : Rh + 1;
}
int main()
{
Tree T;
int i, n;
scanf("%d", &n);
for (i = 0; i < n; i++)scanf("%c", &Pre[i]);
getchar();//Read carriage return in buffer
for (i = 0; i < n; i++)scanf("%c", &In[i]);
T = RCreate(0, 0, n);
printf("\n%d", Height(T));
return 0;
}
Known post order and middle order
This problem requires that according to the post order traversal and middle order traversal results of a given binary tree, the pre order traversal results of the tree are output.
explain:
Root: the root node of subsequent traversal
begin: the starting position of traversing the subtree in middle order
End: the end position of traversing the subtree in middle order
end-i: node number of right subtree
root-1: the sum of the number of nodes in the left subtree and the right subtree after removing the root node
Algorithm:
#include <stdio.h>
#include <stdlib.h>
#define N 31
int Post[N], In[N];
typedef struct TreeNode
{
int data;
struct TreeNode* lchild, * rchild;
}*Tree;
Tree Create(int root, int begin, int end)
{
Tree T;
int i;
if (begin > end)return NULL;
T = (Tree)malloc(sizeof(struct TreeNode));
T->data = Post[root];
for (i = begin; Post[root] != In[i]; i++);
T->lchild = Create(root - 1 - (end - i), begin, i - 1);
T->rchild = Create(root - 1, i + 1, end);
return T;
}
void PreOrder(Tree T)
{
if (!T)return;
printf(" %d", T->data);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
int main()
{
int n, i;
Tree T;
scanf("%d", &n);
for (i = 0; i < n; i++)scanf("%d", &Post[i]);
for (i = 0; i < n; i++)scanf("%d", &In[i]);
T = Create(n - 1, 0, n - 1);
printf("Preorder:");
PreOrder(T);
return 0;
}