subject

Given two trees T1 and T2. If T1 can be changed into T2 through several child exchanges, we call the two trees isomorphic. For example, the two trees given in Fig. 1 are isomorphic, because when we exchange the left and right children of node A, B and G of one tree, we get another tree. Figure 2 is not isomorphic.

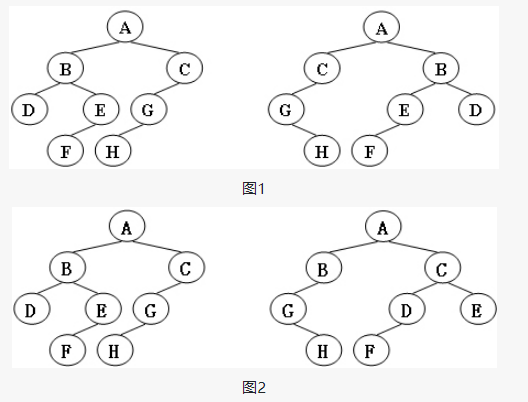
Given two trees, please judge whether they are isomorphic.

Input format:

Input gives information about two binary trees. For each tree, a non-negative integer NN ( Le 10 < 10) is given in one line, i.e. the node number of the tree (assuming that the node is from 0 to N-1N_1 number); then the NN line, the ii line corresponding to the number of the ii node, gives a capital letter stored in the node, the number of the left child node, and the right child node. Number. If the child's node is empty, give "-" in the corresponding position. The data given are separated by a space. Note: The Title ensures that the letters stored in each node are different.

Output format:

If the two trees are isomorphic, output "Yes" or "No".

Input Sample 1 (corresponding to Figure 1):

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

Output Sample 1:

Yes

Input Sample 2 (corresponding to Figure 2):

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

Output Sample 2:

No

Solution Thought

1. Binary Tree Representation
2. Building Binary Trees
3. Isomorphism discrimination

Binary Tree Representation

Static linked list (physical array storage, but learn from the way linked list)
As shown in the figure, the right child of A is B (the subscript of B is 1), the left child of B is C (the subscript is 2), the right child is D (the subscript is 3), and the node without children is marked as -1.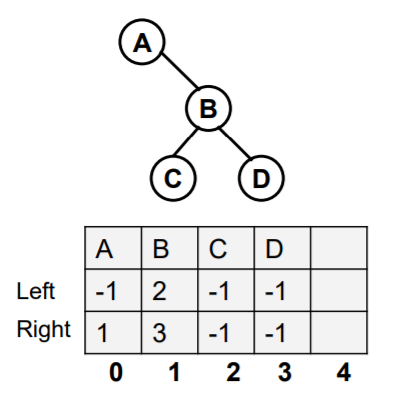

#define MaxTree 10
#define ElementType char
#define Tree int
#define Null -1

struct TreeNode{
	ElementType Element;	//Elements of Nodes
	Tree Left;				//Left child position
	Tree Right;				//Right child position
}T1[MaxTree],T2[MaxTree]	//Define two arrays of MaxTree size

Note that Left and Right are not pointers and that NULL (value 0) cannot be used to indicate that the node has no children, because 0 is also the location of the array. So define a Null=-1 to represent the absence of children.

Program Framework Building

int main()
{
	Tree R1,R2;
	 //Building Binary Tree 1
	R1=BuildTree(T1);
	 //Building Binary Tree 2
	R2=BuildTree(T2);
	 //Identify isomorphism and output
	if(Isomorphic(R1,R2))
		printf("Yes\n");
	else
		printf("No\n");
	 return 0;
}

How to Build Binary Trees

Tree BuildTree( struct TreeNode T[] )
{ 
	scanf("%d\n",&N);	//Read in an integer N
	if(N) {				//N is not zero, continue reading data

		for (i=0;i<N;i++){	//Read in the information of N nodes
			scanf("%c %c %c\n", &T[i].Element, &cl, &cr);

		}
		
		Root = ???
	}
	return Root;		//Return to the root of the tree
}

The non-root node must have other nodes pointing to it, that is, the node without other nodes pointing to is the root node.

Tree BuildTree( struct TreeNode T[] )
{ 
	Tree Root;
	int N,i;
	int *check;
	char cl,cr;
	scanf("%d\n",&N);	//Read in an integer N
	check=(int*)malloc(N*sizeof(int));
	if(N) {				//N is not zero, continue reading data
		for (int i=0;i<N;i++) 
			check[i] = 0;	//check for each node is set to 0
		for (i=0;i<N;i++){	//Read in the information of N nodes
			scanf("%c %c %c\n", &T[i].Element, &cl, &cr);
			if (cl!='-'){				//cl is not - - that means there's a left son.
				T[i].Left = cl-'0';		//The cl read in is a character, -'0'gives an integer.
				check[T[i].Left] = 1;	//check of a node pointed to by another node is set to 1
			}else {
				T[i].Left = Null;		//cl is -, which means there is no left son.
			}
			if (cr!='-'){				
				T[i].Right = cr-'0';		
				check[T[i].Right] = 1;	
			}else 
				T[i].Right = Null;	
		}
		for (i=0;i<N;i++)
			if (!check[i])	//The node where check is still zero is the root node. 
				break;
		Root = i;
	}else{
		return Null;
	}
	return Root;		//Return to the root node
}

How to Discriminate Binary Tree Isomorphism

int Isomorphic ( Tree R1, Tree R2 )
{
 if ((R1==Null)&&(R2==Null)) /* Two empty trees are isomorphic */
	return 1;
 if (((R1==Null)&&(R2!=Null))||((R1!=Null)&&(R2==Null)))
	return 0; /* One of the empty trees must have different structures. */
 if (T1[R1].Element!=T2[R2].Element)
	return 0; /* Different root nodes and different structures */
 if (( T1[R1].Left==Null)&&( T2[R2].Left==Null))
	/* If the left subtree is empty, the right subtree is isomorphic. */
	return Isomorphic(T1[R1].Right,T2[R2].Right);
 if (((T1[R1].Left!=Null)&&(T2[R2].Left!=Null))&&((T1[T1[R1].Left].Element)==(T2[T2[R2].Left].Element)))
	/* If the left subtree is not empty and the left element is the same, the left subtree is isomorphic or the right subtree is isomorphic.*/
	return (Isomorphic( T1[R1].Left, T2[R2].Left ) && Isomorphic( T1[R1].Right, T2[R2].Right));

 else /* Discrimination of Left and Right Isomorphism */
	return (Isomorphic( T1[R1].Left, T2[R2].Right) && Isomorphic( T1[R1].Right, T2[R2].Left));

}

Submission of results