Interface:
public interface StringDistance {
public float getDistance(String s1, String s2) ;
}Method class:
public class JaroWinklerDistance implements StringDistance {
private float threshold = 0.7f;
private int[] matches(String s1, String s2) {
String max, min;
if (s1.length() > s2.length()) {
max = s1;
min = s2;
} else {
max = s2;
min = s1;
}
int range = Math.max(max.length() / 2 - 1, 0);
int[] matchIndexes = new int[min.length()];
Arrays.fill(matchIndexes, -1);
boolean[] matchFlags = new boolean[max.length()];
int matches = 0;
for (int mi = 0; mi < min.length(); mi++) {
char c1 = min.charAt(mi);
for (int xi = Math.max(mi - range, 0), xn = Math.min(
mi + range + 1, max.length()); xi < xn; xi++) {
if (!matchFlags[xi] && c1 == max.charAt(xi)) {
matchIndexes[mi] = xi;
matchFlags[xi] = true;
matches++;
break;
}
}
}
char[] ms1 = new char[matches];
char[] ms2 = new char[matches];
for (int i = 0, si = 0; i < min.length(); i++) {
if (matchIndexes[i] != -1) {
ms1[si] = min.charAt(i);
si++;
}
}
for (int i = 0, si = 0; i < max.length(); i++) {
if (matchFlags[i]) {
ms2[si] = max.charAt(i);
si++;
}
}
int transpositions = 0;
for (int mi = 0; mi < ms1.length; mi++) {
if (ms1[mi] != ms2[mi]) {
transpositions++;
}
}
int prefix = 0;
for (int mi = 0; mi < min.length(); mi++) {
if (s1.charAt(mi) == s2.charAt(mi)) {
prefix++;
} else {
break;
}
}
return new int[] { matches, transpositions / 2, prefix, max.length() };
}
public float getDistance(String s1, String s2) {
int[] mtp = matches(s1, s2);
float m = (float) mtp[0];
if (m == 0) {
return 0f;
}
float j = ((m / s1.length() + m / s2.length() + (m - mtp[1]) / m)) / 3;
float jw = j < getThreshold() ? j : j + Math.min(0.1f, 1f / mtp[3])
* mtp[2] * (1 - j);
return jw;
}
/**
* Sets the threshold used to determine when Winkler bonus should be used.
* Set to a negative value to get the Jaro distance.
*
* @param threshold
* the new value of the threshold
*/
public void setThreshold(float threshold) {
this.threshold = threshold;
}
/**
* Returns the current value of the threshold used for adding the Winkler
* bonus. The default value is 0.7.
*
* @return the current value of the threshold
*/
public float getThreshold() {
return threshold;
}
}Of course, you can also directly use the method of jar plug-in
api address of this method:
http://lucene.apache.org/core/3_0_3/api/contrib-spellchecker/org/apache/lucene/search/spell/JaroWinklerDistance.html
http://lucene.apache.org/core/3_0_3/api/contrib-spellchecker/org/apache/lucene/search/spell/StringDistance.html
Jaro Winkler distance algorithm
This is a method to calculate the similarity between two strings. I must have heard of edit distance. Jaro inkler distance is an extension of Jaro Distance. Jaro Distance (Jaro 1989;1995) is said to be used to determine whether the two names on the health record are the same. It is also said to be used for census. Whatever you do, it doesn't matter, Let's first look at the definition of Jaro Distance.
Jaro Distance for two given strings S1 and S2 is:
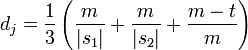
m is the number of matching characters;
t is the number of transpositions.
If two characters from S1 and S2 are not more than
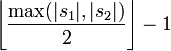
When, we think that the two strings match; These matching characters determine the number of transpositions T, which is simply half of the number of matching characters in different orders, that is, the number of transpositions T. for example, MARTHA and MARHTA characters are matched, but among these matching characters, t and H need transposition to change MARTHA into MARHTA, so t and H are matching characters in different orders, t=2/2=1
Then the Jaro Distance of these two strings is:
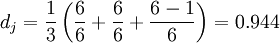
Jaro Winkler gives higher scores for the same string at the beginning. He defines a prefix p and gives two strings. If the prefix part has the same length, Jaro Winkler distance is:
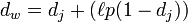
dj is the Jaro Distance of two strings
Is the same length as the prefix, but specifies a maximum of 4
p is the constant for adjusting the score, which must not exceed 0.25, otherwise dw may be greater than 1. Winkler defines this constant as 0.1
Thus, the Jaro Winkler distance of MARTHA and MARHTA mentioned above is:
dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961
The above information is from Wikipedia: